Элементы общей топологии
Курсовая работа
на тему: «Элементы общей топологии»
Введение
Топология – одна из самых молодых ветвей геометрии. Топология является одним из самых абстрактных разделов современной математики. Примерно за сто лет её существования в ней достигнуты результаты, важные для многих разделов математики.
Топология (от греческого «τοποξ» – место, окрестность, «λογοξ» – закон) – раздел математики, изучающий идеи непрерывности. В топологии впервые даются строгие определения таких фундаментальных понятий геометрии, как линия и поверхность. Предметом топологии являются свойства фигур, сохраняющиеся при гомеоморфизмах, то есть взаимно однозначных и непрерывных в обе стороны отображениях. Топология, как наука возникла из потребностей связанных с математическим анализом. Эта наука, хотя и считается молодой, на самом деле известна уже давно, именно благодаря тесным связям с математическим анализом. Идеи топологии идут от работ таких крупных математиков 19 в. как Риммман, Пуанкаре, Кантор, Эйлер. Развитие топологии идёт бурными темпами и в большом числе направлений, этот процесс не окончен в настоящее время, хотя ряд крупных проблем, стоящих перед топологией, успешно решен. Топологические методы стали мощным инструментом математического исследования. Топологический подход позволяет упростить многие доказательства фундаментальных теорем классической математики и обобщить эти теоремы на более широкие классы пространств.
Геометрия школьного курса имеет дело в основном со свойствами фигур, связанными с понятиями длины, площади, объема-то есть метрическими свойствами фигур. Лишь очень немногие теоремы и задачи школьного курса геометрии рассматривают свойства иного характера. Топология как раз и является разделом геометрии, изучающим свойства фигур, которые могут быть установлены без измерения и сравнения величин, но при этом имеющие геометрический смысл.
Целью первой главы курсовой работы было рассмотреть основные элементы общей топологии.
Задачи:
дать определение топологического пространства;
рассмотреть свойства топологических пространств;
охарактеризовать топологические преобразования.
Во второй главе работы мы попытались рассмотреть топологические свойства поверхностей. Были поставлены следующие задачи:
дать определение двумерного многообразия;
рассмотреть эйлерову характеристику поверхности;
охарактеризовать ориентируемые и неориентируемые поверхности.
1. Элементы общей топологии
1.1 Понятие топологического пространства
1.1.1 Понятие метрического пространства
Определение 1. Декартово произведение множеств А и В определяется как множество всех упорядоченных пар (х, у), где хА, уВ, то есть
АВ = (х, у)| хА, уВ.
В частности, возможно А = В.
Определение 2. Говорят, что в множестве Х задана метрика , если определено отображение
: Х Х R,
удовлетворяющее следующим аксиомам:
1. х, у Х (х, у) 0, причем (х, у) = 0 х = у.
2. х, у Х (х, у) = (у, х).
3. х, у, z Х { (х, у) + (у, z) (х, z)}.
Условия 1, 2, 3 называются аксиомами метрики, при этом условие 2 называется аксиомой симметрии, а 3 – аксиомой треугольника.
Определение 3. Множество Х с заданной на нем метрикой называется метрическим пространством и обозначается (Х, ).
В тех случаях, когда ясно, о какой метрике идет речь, метрическое пространство (Х,) обозначают просто Х.
Число (х, у) называют расстоянием между точками х и у в пространстве Х.
1.1.2 Примеры метрических пространств
Пример 1. Определим для элементов произвольного непустого множества Х расстояние следующим образом:
(х,
у) =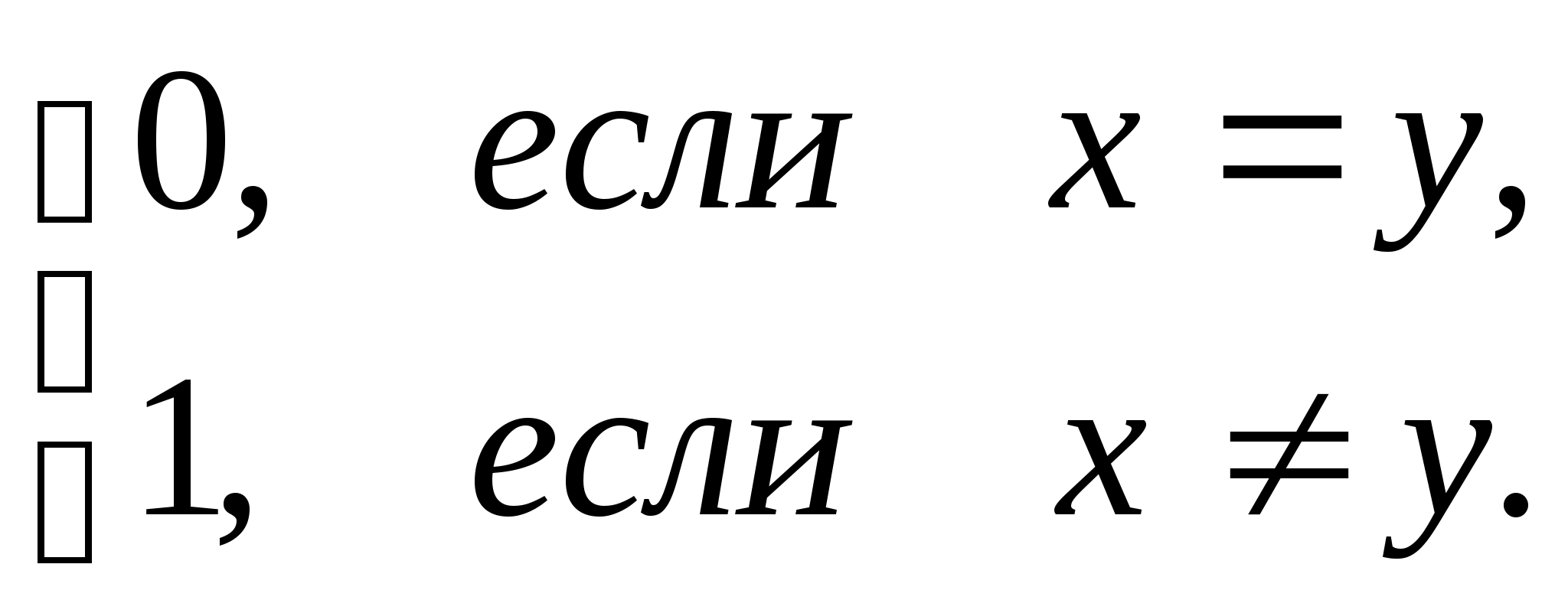 .
.
Очевидно, аксиомы 1 – 3 выполняются, а, следовательно, (Х, ) – метрическое пространство.
Пример 2. Множество действительных чисел R с расстоянием
(х, у) = (у – х)2 не является метрическим пространством.
Действительно не выполняется третья аксиома. Например, для трех точек 2, 3 и 4 получим:
(2, 3) = (3 – 2)2 = 1, (3, 4) = (4 – 3)2 = 1,
(2, 4) = (4 – 2)2 = 4 и (2, 3) + (3, 4) < (2, 4).
Определение 1. Пусть (Х, ) – метрическое пространство, х>0> Х,
r > – действительное число. Назовём открытым шаром с центром в точке х>0> и радиусом r множество
U (x>0>, r) = x | x X, (x, x>0>) r .
Определение 2. Подмножество G Х будем называть открытым в
(Х, ), если любая его точка является центром некоторого открытого шара, содержащегося в G.
Пустое множество также считаем открытым множеством.
Определение 3. Окрестностью точки А метрического пространства будем называть любое открытое множество, содержащее эту точку.
Обозначим совокупность всех открытых множеств в (Х, ) просто Ф>>.
Тогда имеет место следующая теорема.
Теорема. 1) Объединение любой совокупности {G>>} множеств из Ф>> принадлежит Ф>>.
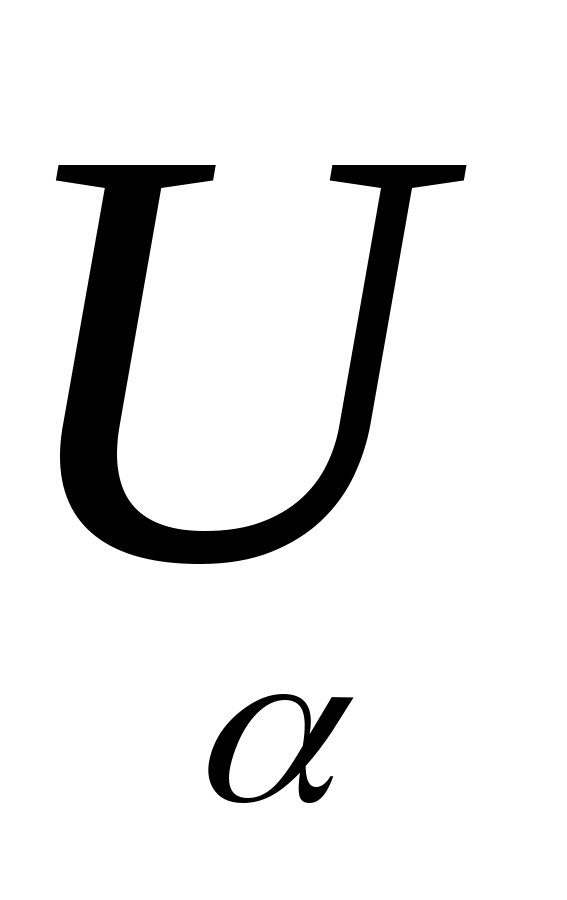 G
G
Ф>>.
Ф>>.
2) Пересечение любых двух множеств G>1> и G>2> из Ф>> принадлежит Ф>>.
G>1> G>2> Ф>>.
3) Метрическое пространство Х – открытое множество, то есть
Х Ф>>, Ф>>.
Доказательство.
1) Пусть
 .
Обозначим
.
Обозначим
G
=
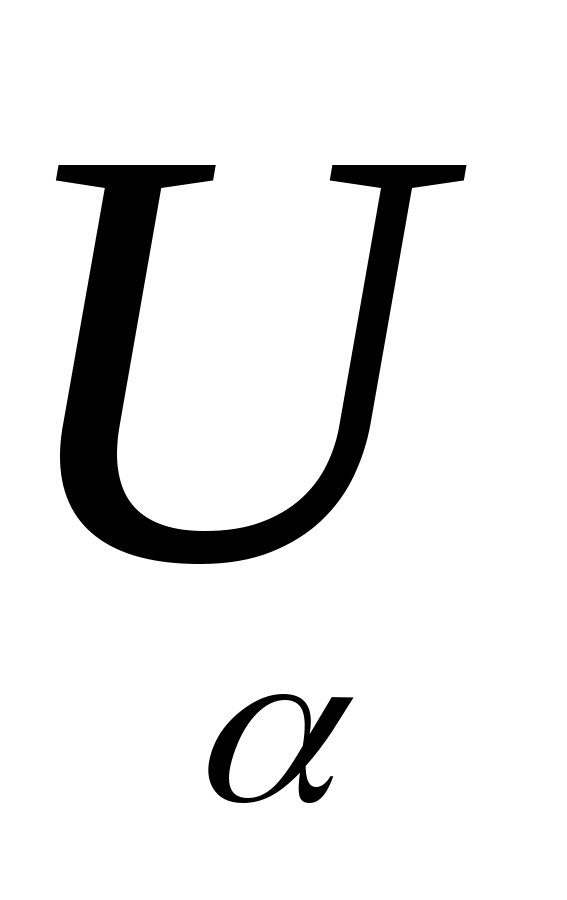
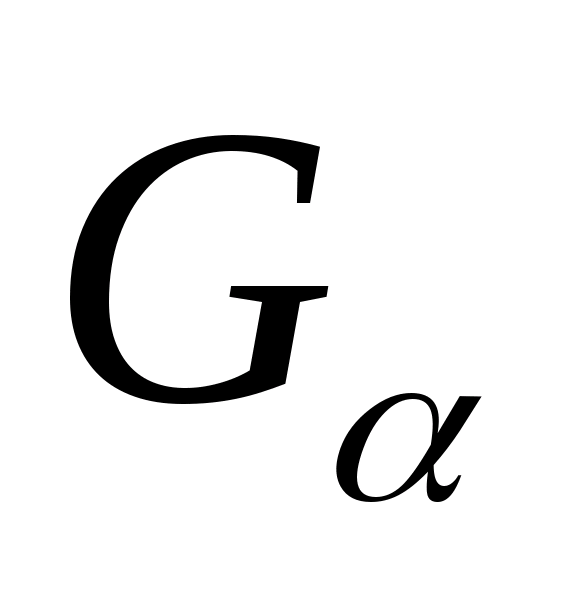 .
.
Возьмём
произвольную точку х>0>
G.
Тогда существует такое >0>,
что х>0>
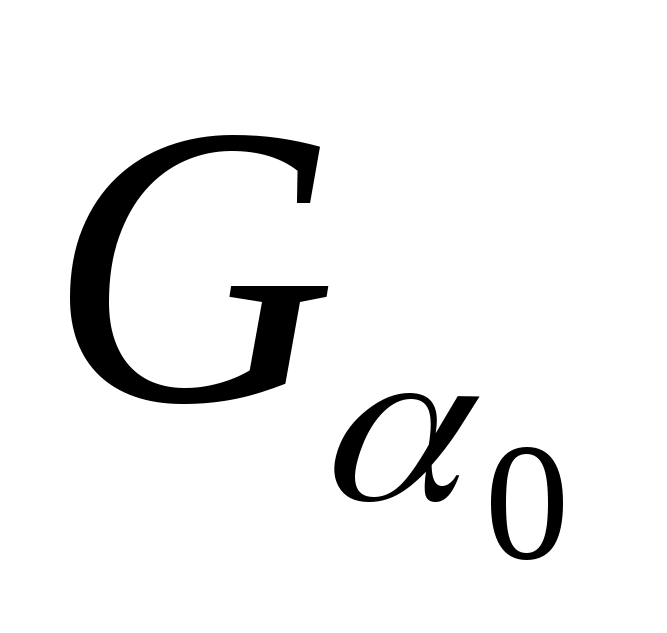 ,
и так как
,
и так как
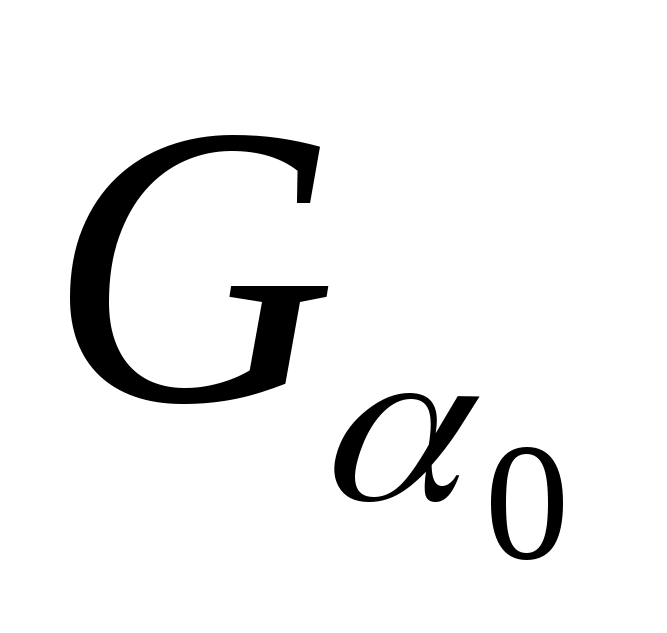
Ф>>,
то найдётся число r>0>,
что
Ф>>,
то найдётся число r>0>,
что
U
(х>0>,
r>0>)
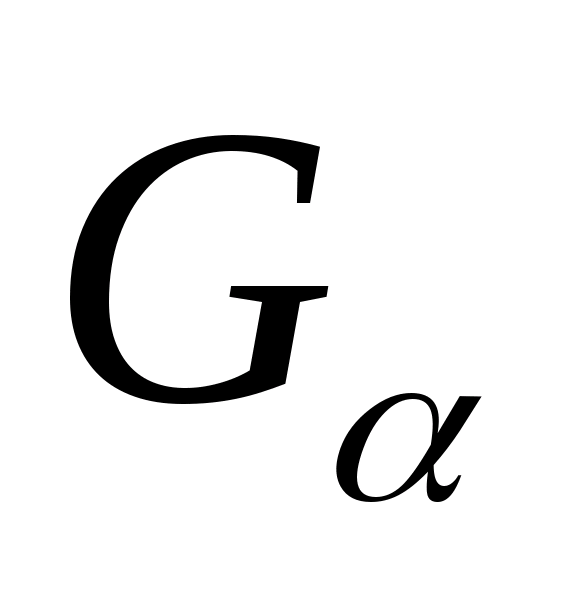 .
.
Так
как G >0>
G,
то U
(х>0>,
r>0>)
G.
>0>
G,
то U
(х>0>,
r>0>)
G.
Итак, G – открытое множество.
2)
Пусть G
= G>1>
G>2>,
где G>1>,
G>2
>
Ф>>
и G
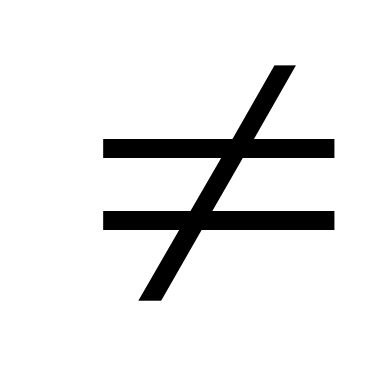 .
.
Если х>0> G, то х>0> G>1 >и х>0> G>2>.
Тогда существуют такие радиусы r>1> и r>2>, что
U(х>0>, r>1>) G>1,> U(х>0>, r>2>) G>2>.
Обозначим r = min {r>1>, r>2>}, тогда
U (х>0>, r) G>1> G>2> = G.
Итак, G – открытое множество.
3. Так как всегда можно представить
Х
=
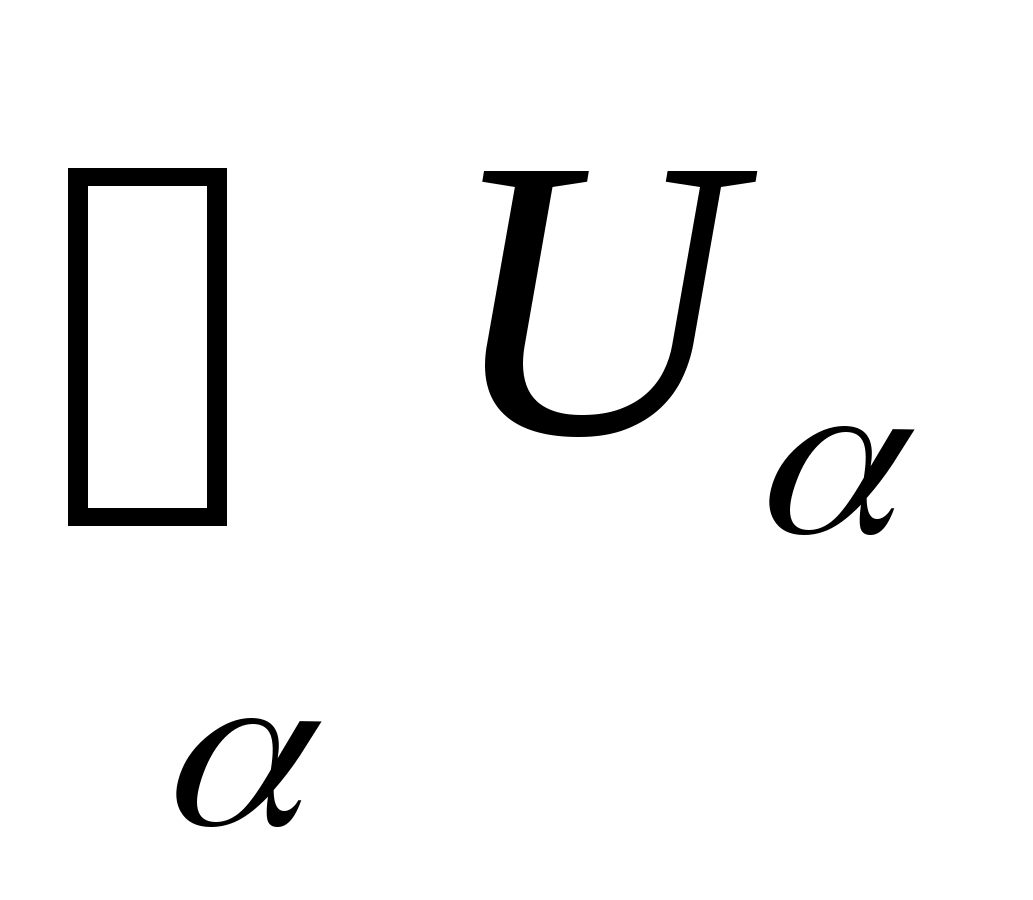 ,
,
где
U>>
– открытый шар радиуса r,
с центром в точке
 ,
объединение рассматривается по всем
точкам пространства, то в силу 1 получим,
что пространство Х – открыто. Пустое
множество мы предполагаем всегда
открытым.
,
объединение рассматривается по всем
точкам пространства, то в силу 1 получим,
что пространство Х – открыто. Пустое
множество мы предполагаем всегда
открытым.
В дальнейшем описанное нами семейство Ф>> всех открытых множеств в метрическом пространстве (Х, ) будем называть топологией, индуцированной метрикой в Х.>.>
1.1.3 Определение и примеры топологических пространств
Многие понятия теории метрических пространств (предел, предельная точка, точка прикосновения, замыкание множества, граница множества, непрерывность и т.д.) вводятся, опираясь на понятие окрестности или, что тоже самое, на понятие открытого множества. Понятие окрестность и открытое множество определяются с помощью метрики.
Свойства открытых множеств метрического пространства принимаются в качестве аксиом. Этот путь приводит нас к топологическим пространствам, по отношению к которым метрические пространства представляют собой частный случай.
Определение
1.
Пусть Х – непустое множество элементов
произвольной природы, Ф = {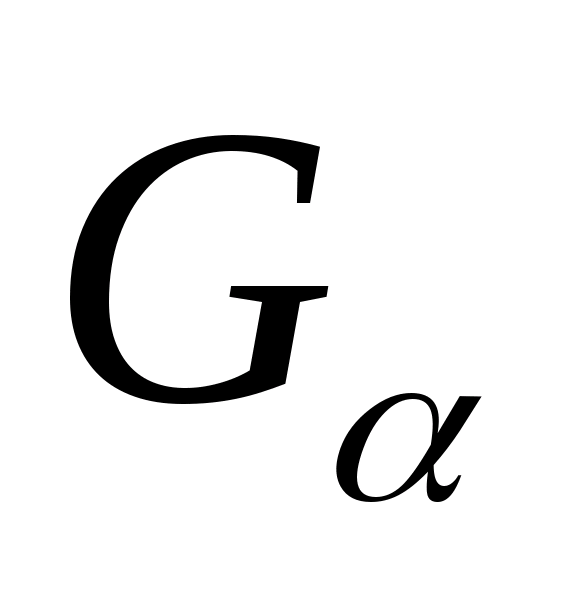 }
– семейство подмножеств множества Х,
удовлетворяющее следующим аксиомам:
}
– семейство подмножеств множества Х,
удовлетворяющее следующим аксиомам:
1. Само множество Х и пустое множество принадлежат семейству Ф.
2. Объединение любого семейства множеств из Ф также принадлежит Ф.
3. Пересечение любых двух множеств из Ф также принадлежит Ф.
Тогда семейство Ф называется топологией или топологической структурой.
Пара (Х, Ф) или, другим словами, множество Х, в котором задана некоторая топология, называется топологическим пространством.
Элементы множества Х называются точками топологического пространства, элементы семейства Ф называются открытыми множествами в (Х, Ф).
Когда
не может возникнуть недоразумений,
разрешается просто писать: Х –
топологическое пространство, G – открытое множество, то есть не указывать
постоянно связь с топологией Ф.
– открытое множество, то есть не указывать
постоянно связь с топологией Ф.
Примеры топологических пространств.
Пример 1. Х – произвольное множество. Из аксиомы 1 топологического пространства вытекает, что среди открытых множеств любой топологической структуры в Х обязательно должны быть пустое множество и само множество Х. Очевидно, что для семейства
Ф>т> = {, X},
которое состоит лишь из этих двух множеств, выполняются также и аксиомы 2 и 3.
Поэтому Ф>т> = {, X} является простейшей топологической структурой в Х. Эта топология называется тривиальной, а пара (Х, Ф) тривиальным топологическим пространством. Иногда эту пару называют антидискретным топологическим пространством.
Пример 2. Другой крайностью является так называемое дискретное топологическое пространство (Х, Ф>d>), где Ф>d> представляет собой семейство всех подмножеств множества Х. Очевидно, что и в этом случае все аксиомы 1 – 3 выполняются.
Пример 3. Пусть Х = R3. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусом r, а также всё множество Х и пустое множество.
Очевидно, аксиома 1 выполняется.
Пусть
{U(r>>)}
– любая система открытых множеств.
Тогда их объединением будет шар с центром
О и радиусом r
=
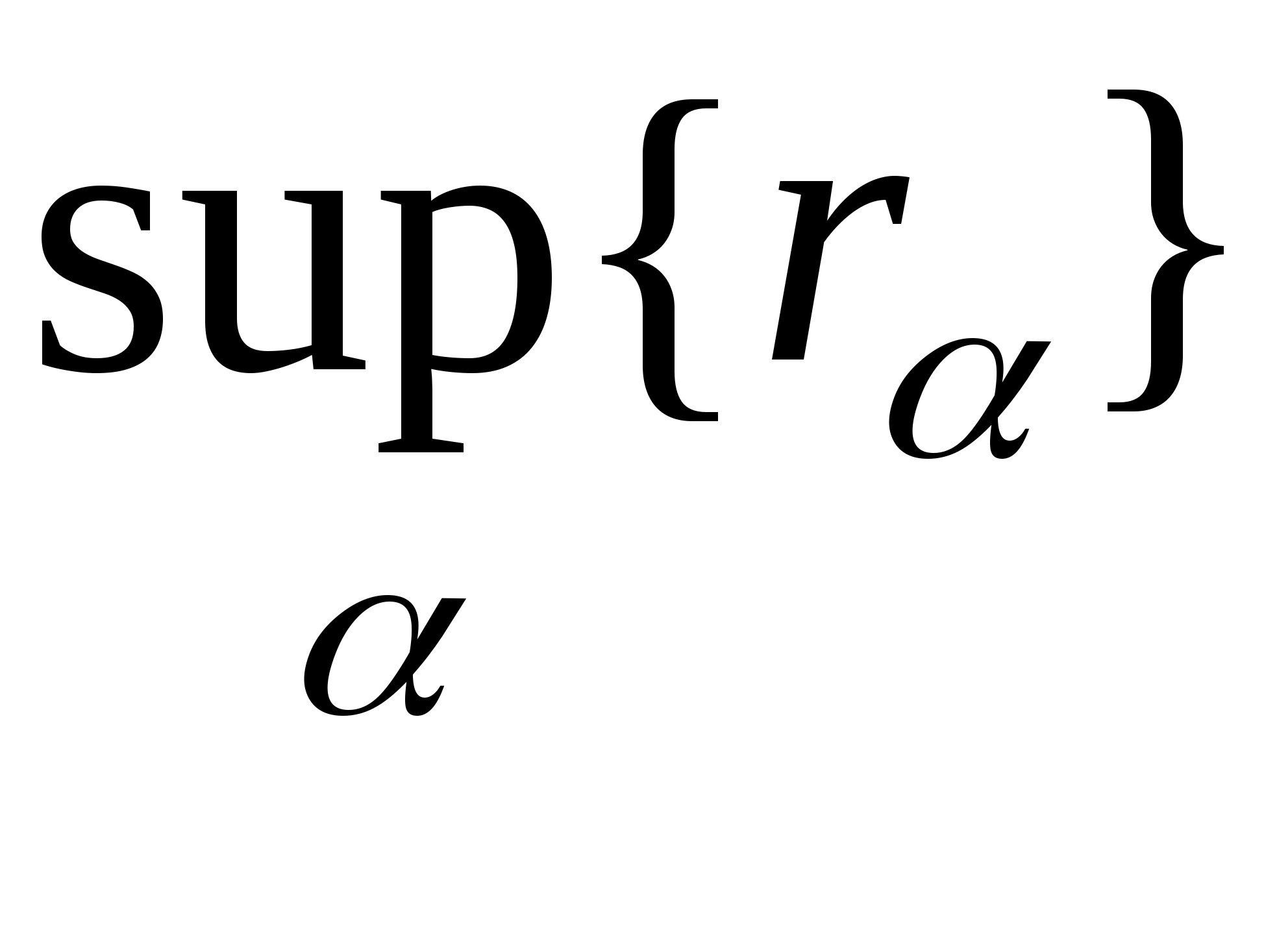 .
.
Если
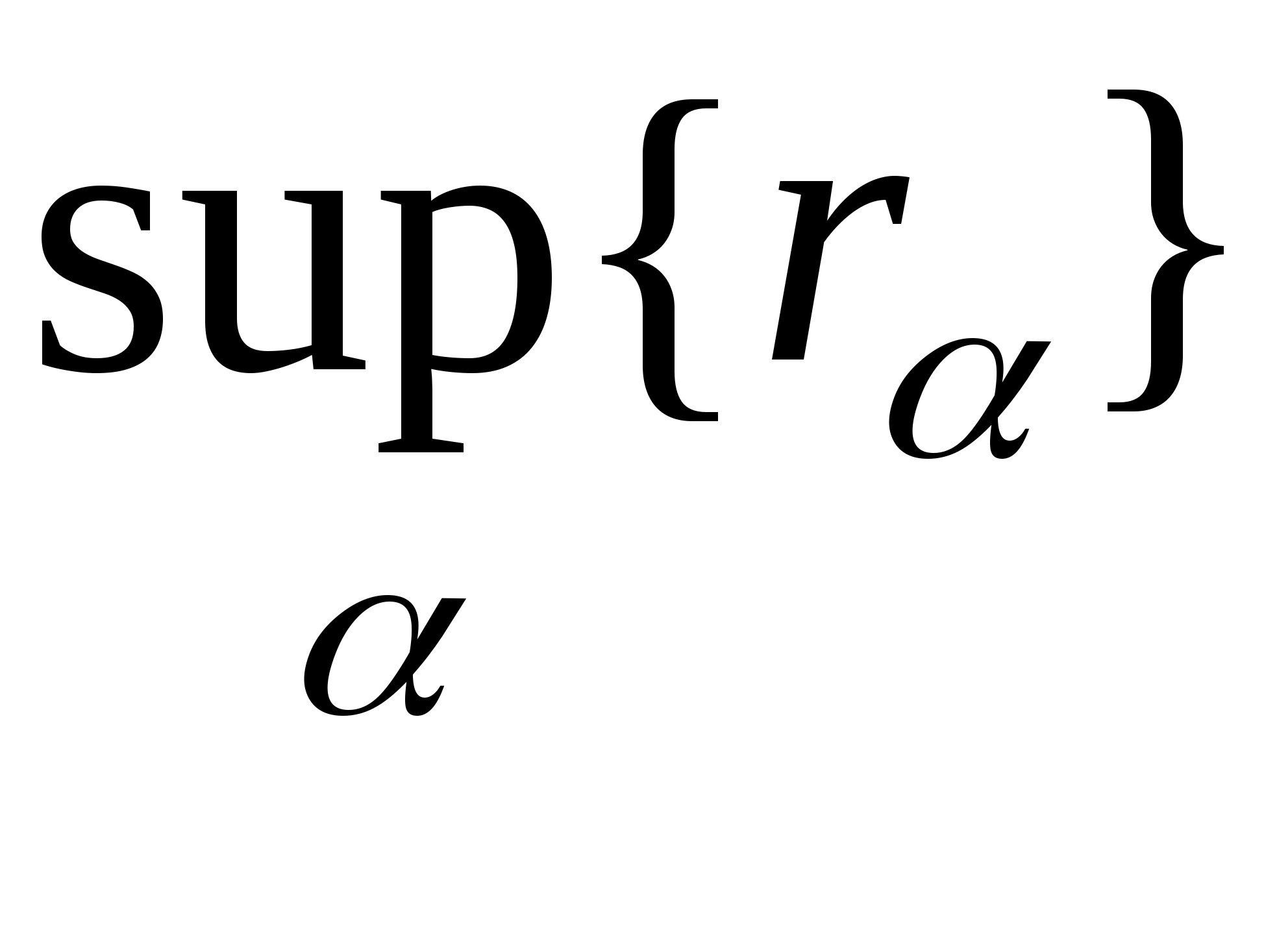 = ,
то U(r)
= X.
= ,
то U(r)
= X.
Следовательно, аксиома 2 выполняется.
Пересечением
двух множеств U(r>1>)
и U(r>2>)
будет множество U(r),
где r
=
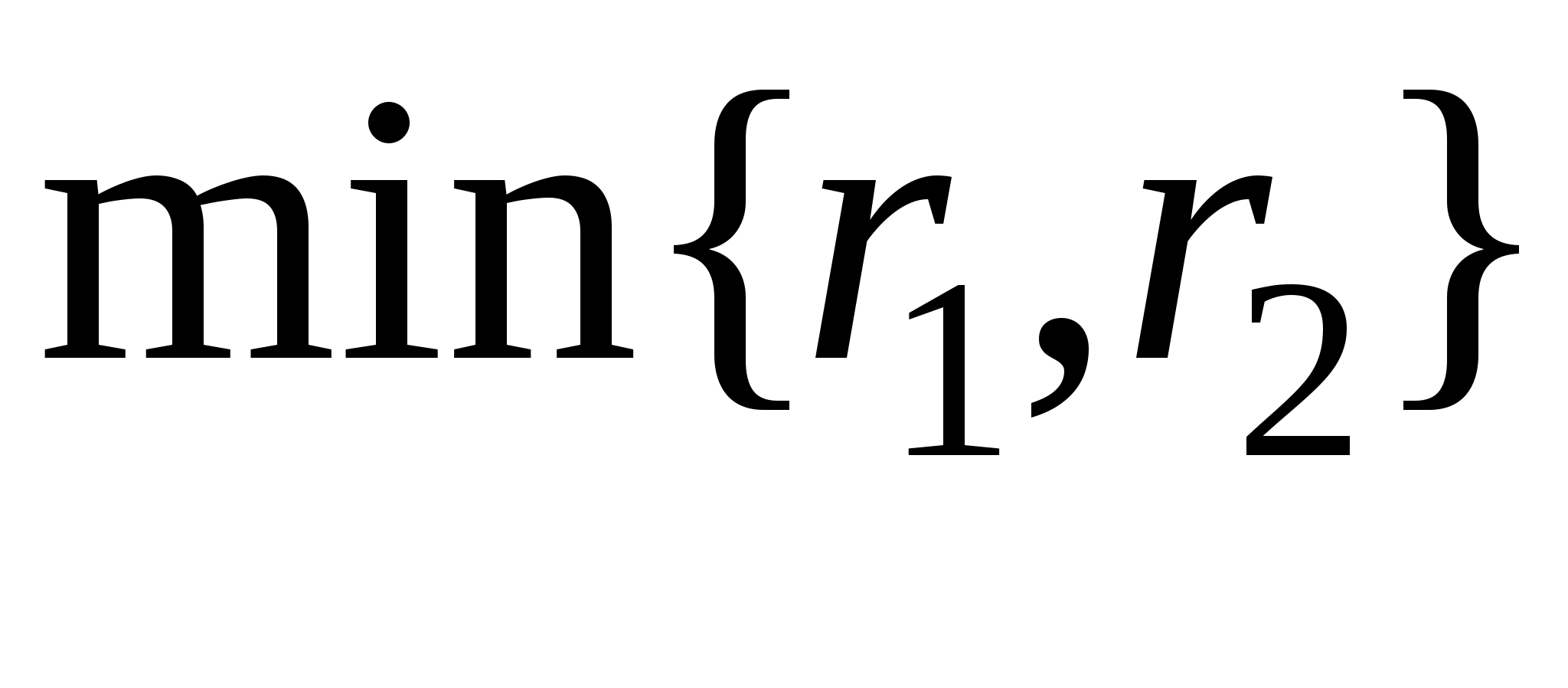 ,
то есть аксиома 3 также выполняется.
,
то есть аксиома 3 также выполняется.
Выделенное нами семейство открытых множеств является топологией в R3, которую иногда называют концентрической.
Определение 2. Пусть в множестве Х введены две топологии Ф>1> и Ф>2>. Говорят, что Ф>1> сильнее Ф>2> (или Ф>2> слабее Ф>1)>, если Ф>2> Ф>1>, то есть любое множество из Ф>2> принадлежит Ф>1>.
Очевидно, самой сильной топологией является дискретная топология, а самой слабой – тривиальная.
А вообще – две топологии на одном и том же множестве могут быть несравнимыми.
Пример.
Х
=
 ,
,
Ф>1>
=
Х,
 ,
,
Ф>2>
,
Х,
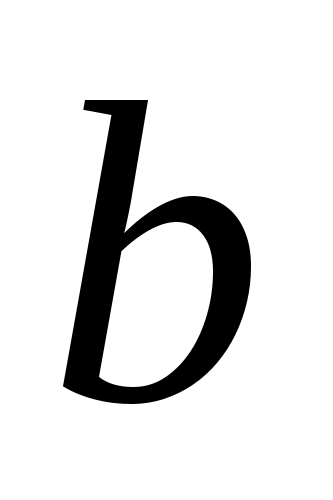 .
.
Топологии Ф>1> и Ф>2> несравнимы.
Теорема
1.
Пересечение произвольного множества
топологий, заданных на Х, является
топологией в Х. Эта топология Ф слабее
любой из данных топологий Ф .
.
Доказательство.
Пусть
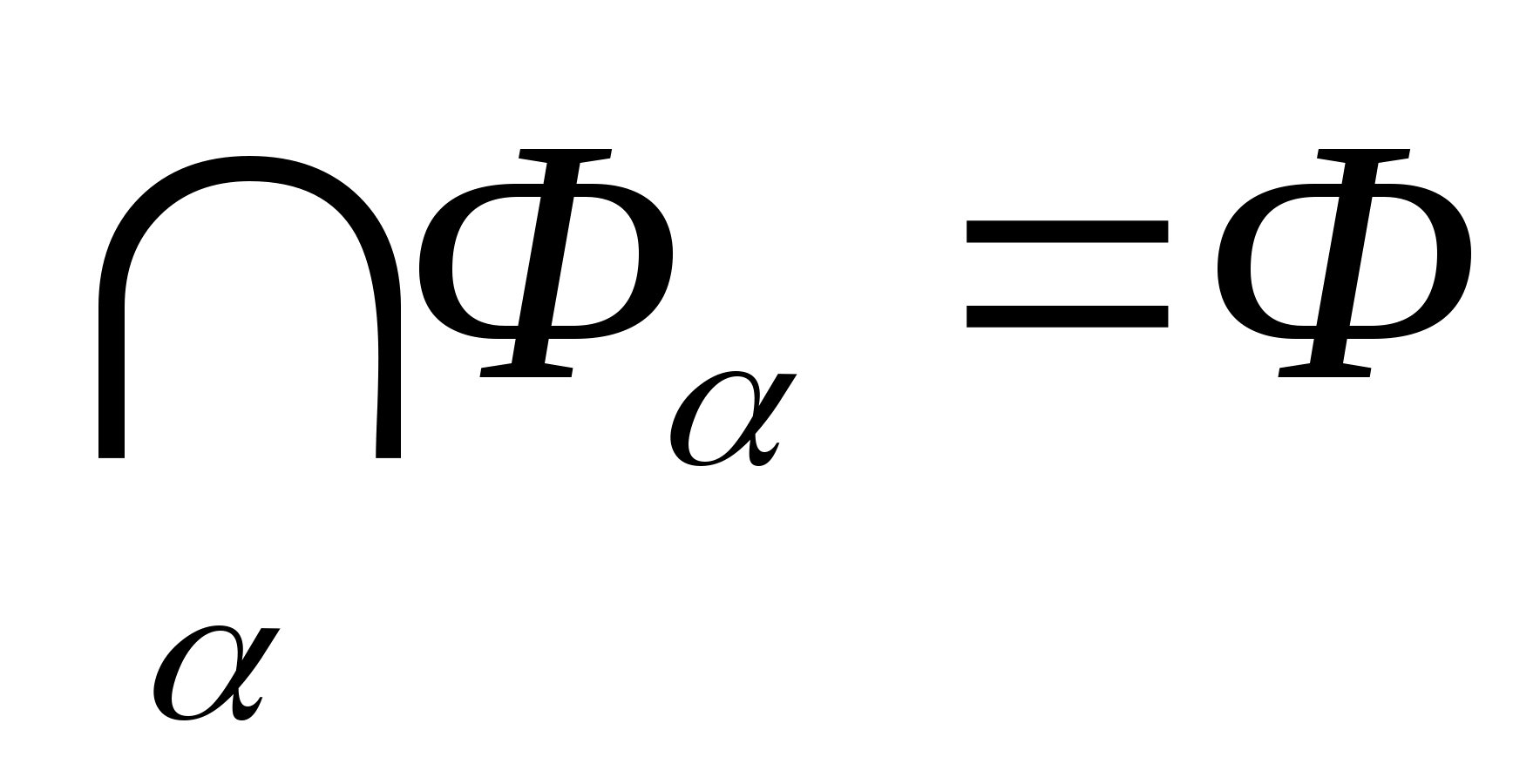 .
.
Так как для любого
{Х
Ф ,
,
то
{X Ф.
Далее,
из того, что каждое Ф замкнуто относительно взятия любых
объединений и конечных пересечений,
следует, что этим свойством обладает и
множество
замкнуто относительно взятия любых
объединений и конечных пересечений,
следует, что этим свойством обладает и
множество
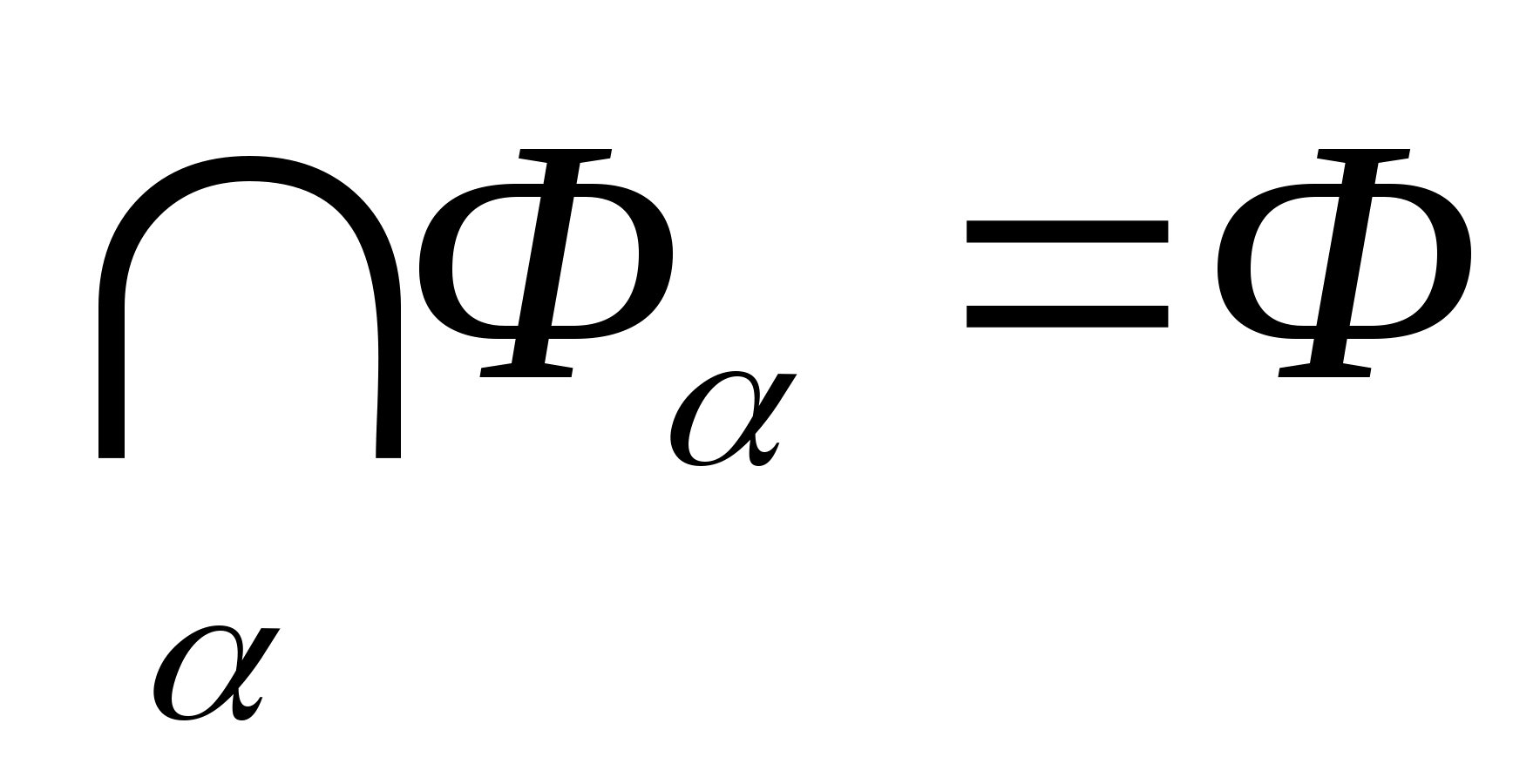 .
.
Теорема 2. Пусть А – произвольная система подмножеств множества Х. Тогда существует минимальная топология в Х, содержащая А.
Действительно, всегда существуют топологии, содержащие А, например, дискретная. Пересечение всех топологий, содержащих А и есть искомая топология. Эта минимальная топология называется топологией, порождённой системой А.
1.2 Свойства топологических пространств
1.2.1 Понятие подпространства
Если У подмножество Х, а (Х, Ф) – топологическое пространство, то на У можно рассматривать топологию
=
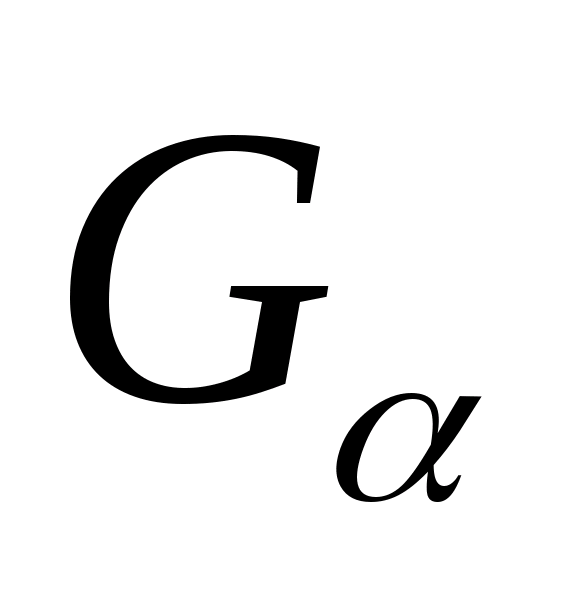
У
G
У
G
Ф .
Ф .
Действительно, обозначим:
S =
=
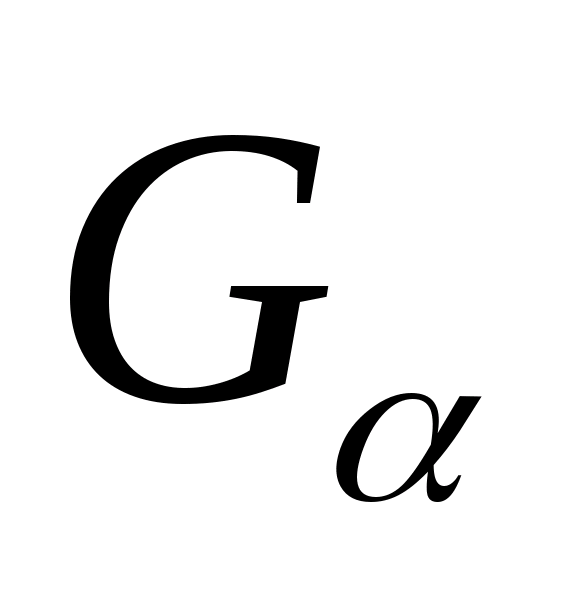
У,
=
S
У,
=
S .
.
1.
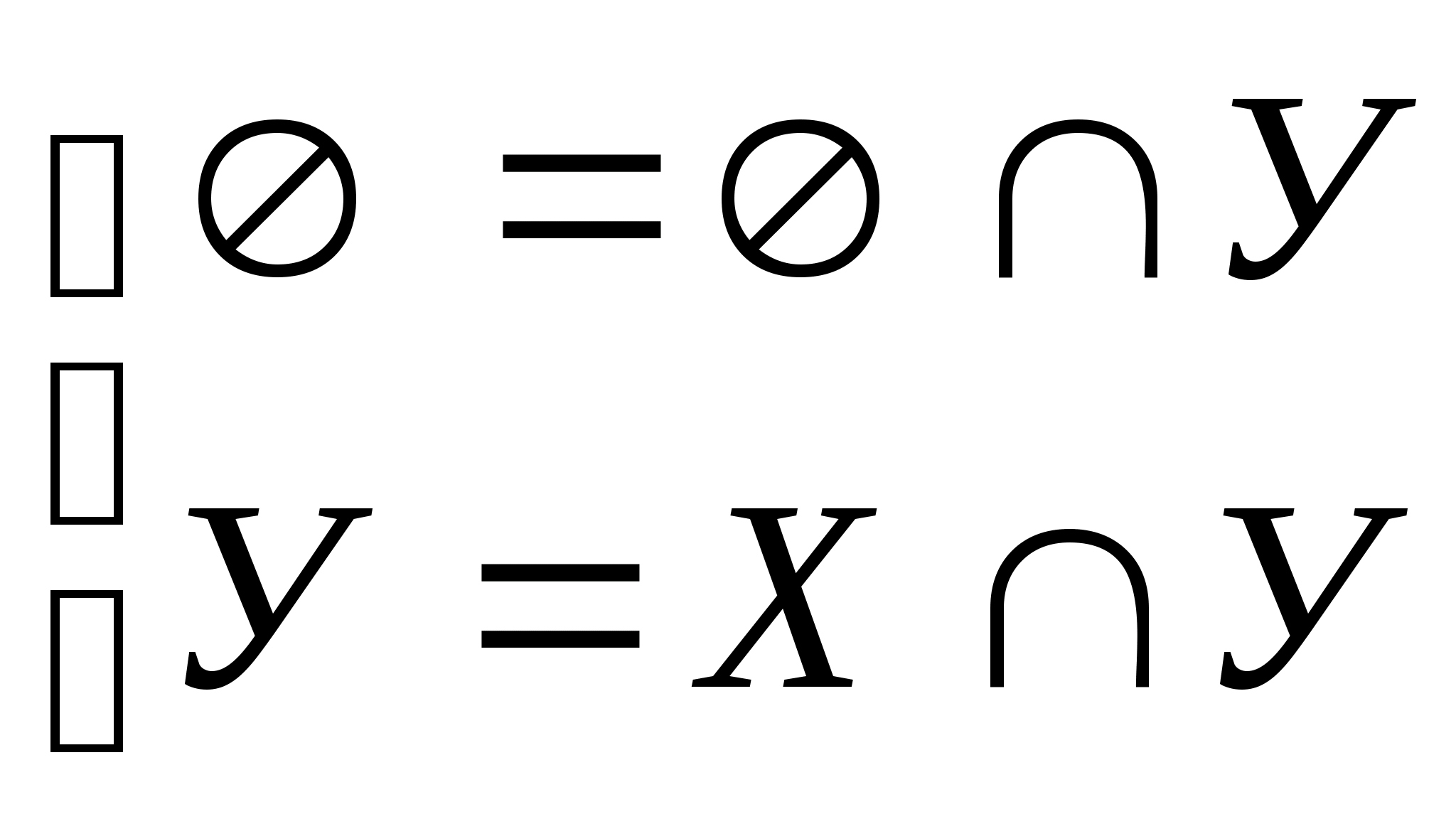
,
У
.
,
У
.
2.
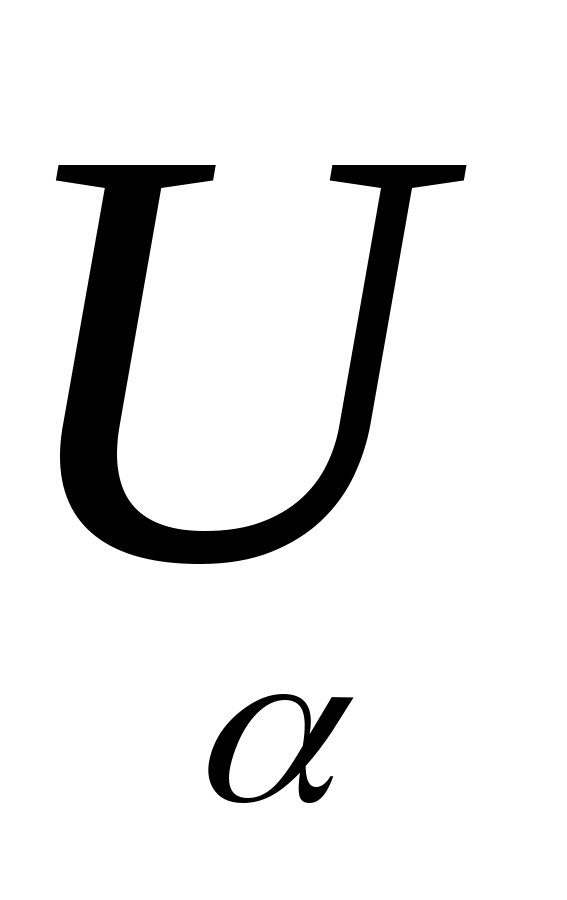 S
S =
=
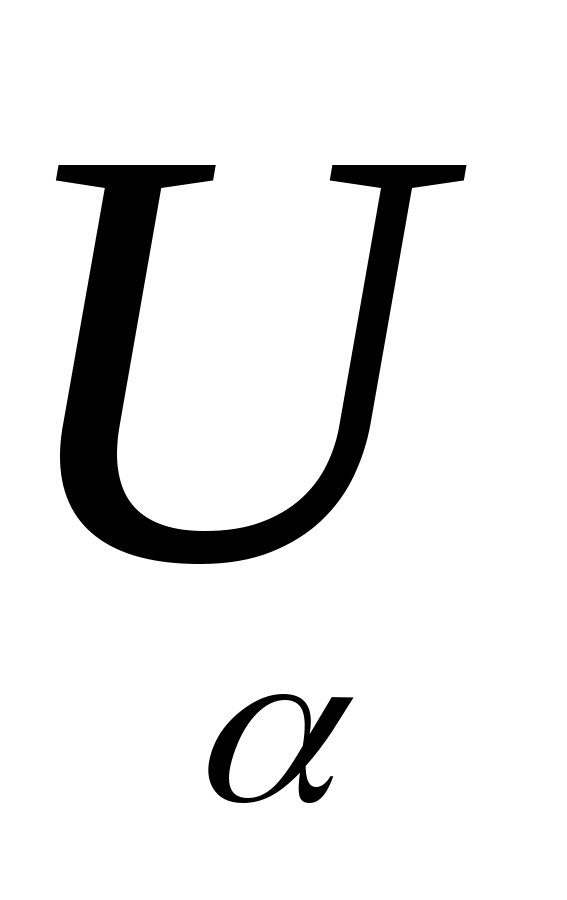 (G
(G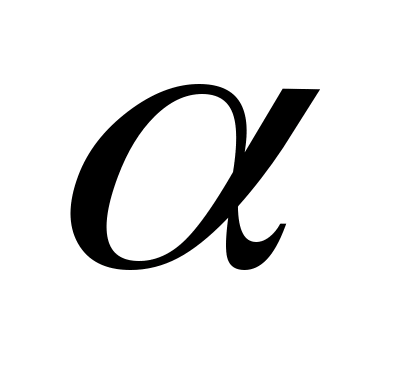
У) = (
У) = (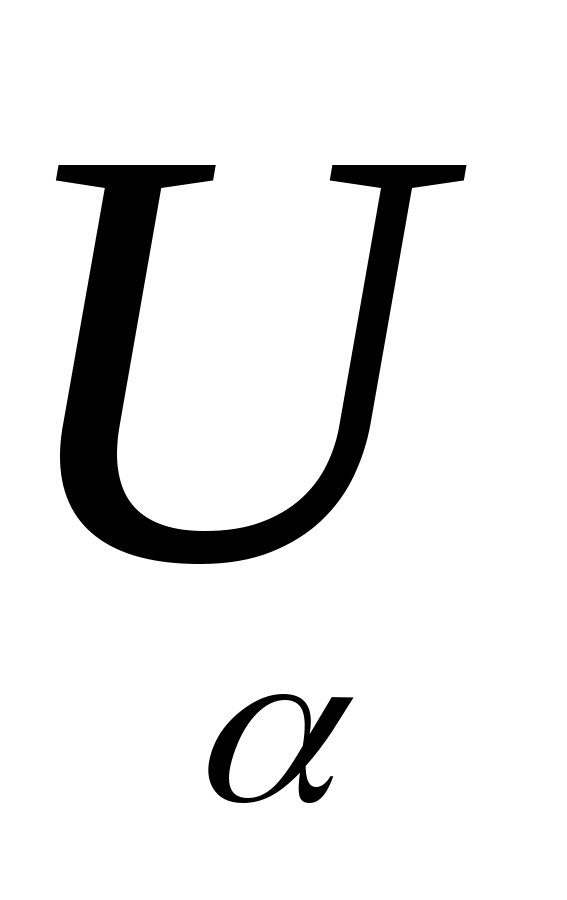 G
G )
У
.
)
У
.
3.
S
S
S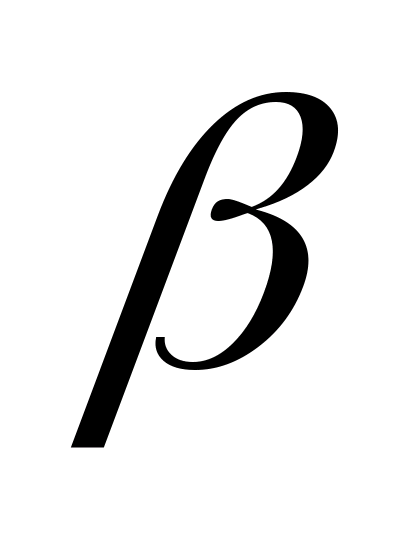 = (G
= (G
У)
(G
У)
(G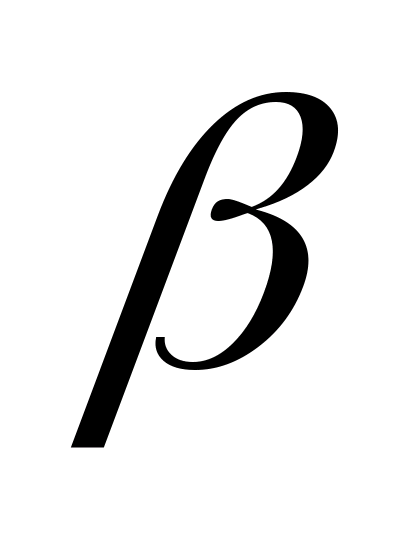
У) = (G
У) = (G G
G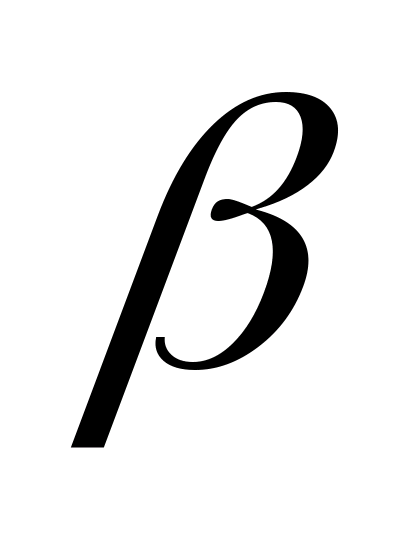 )
У
.
)
У
.
(У, ) – называют топологическим подпространством пространства (Х, Ф), а – топологией, индуцированной топологией Ф.
Пример. Пусть Х = Е3. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусами r, а также все множество Х и пустое множество. Известно, что набор открытых множеств задает топологию Ф>к >на Х, то есть (Х, Ф>к>) топологическое пространство.
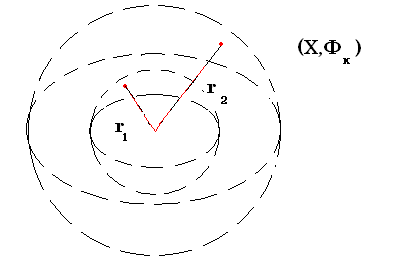
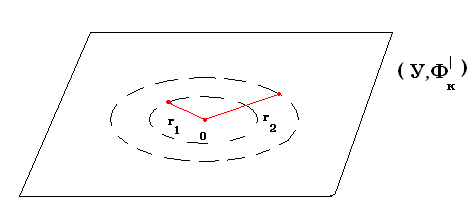
Рассмотрим плоскость, проходящую через точку О и обозначим ее У. Тогда У – подмножество Х и на У индуцируется следующая топология: открытыми множествами будут У, и открытые круги с общим центром О и радиусами r.
1.2.2 Замкнутые множества. Внутренние, внешние и граничные точки
Определение 1. Подмножество А топологического пространства
(Х, Ф) называется замкнутым, если его дополнение Х \ А открытое множество.
Так как дополнение к дополнению множества А есть снова А, то получаем: множество А открыто в том и только в том случае, когда дополнение к нему замкнуто.
Если (Х, Ф) – антидискретное топологическое пространство, то дополнения к Х и к являются единственными замкнутыми множествами, но учитывая, что
Х / Х = , Х / = Х,
получаем: и Х – являются также и замкнутыми множествами.
Х и замкнуты (и одновременно открыты) в любом топологическом пространстве (Х, Ф).
Если Ф – дискретная топология, то любое множество замкнуто и открыто.
Если Х – множество действительных чисел и Ф обычная топология, то есть индуцированная естественной метрикой, то множество
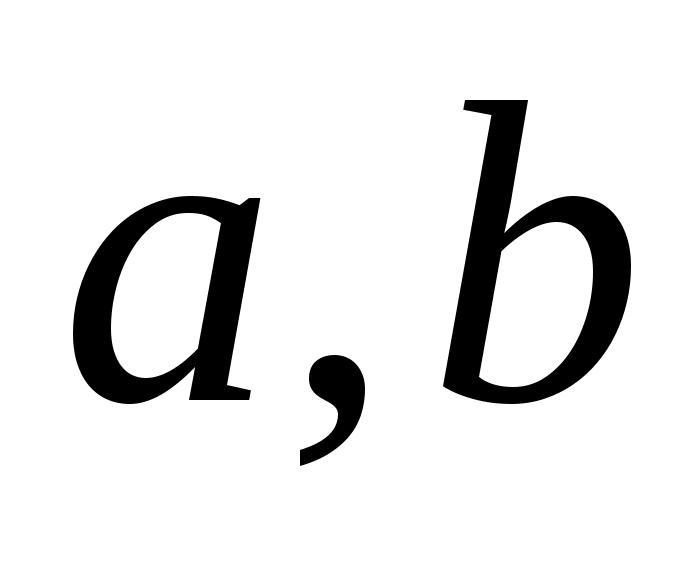 =
х
=
х

х
х
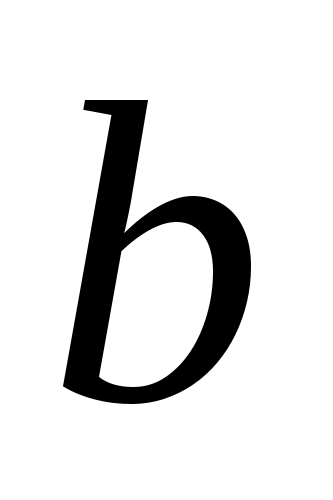
= Х \ ((– ,
= Х \ ((– ,
 )
(
)
(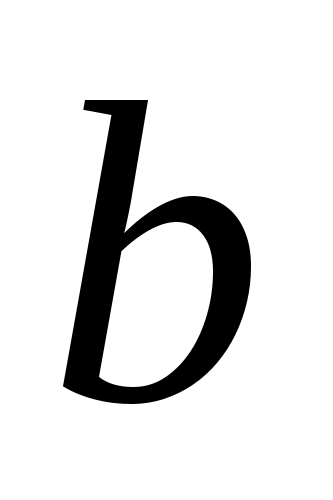 ,
+ ))
,
+ ))
замкнуто.
Используя формулы де Моргана
Х
\
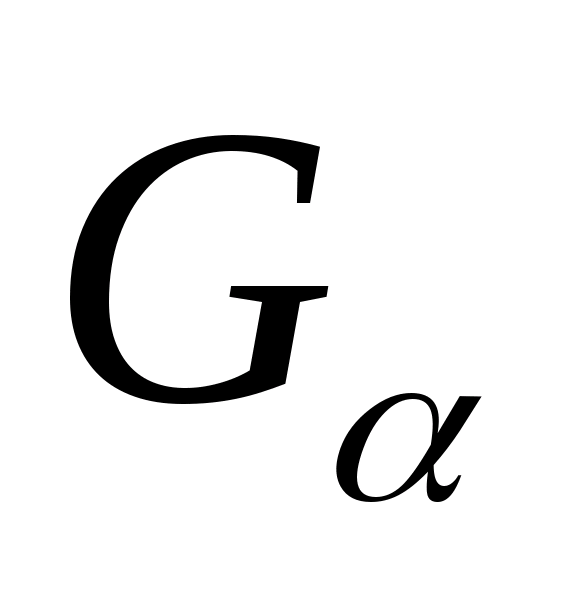 =
(X
\
=
(X
\
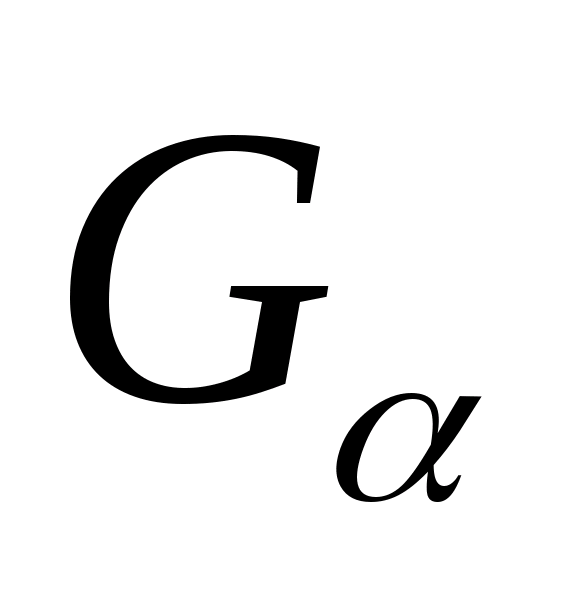 ),
),
Х
\
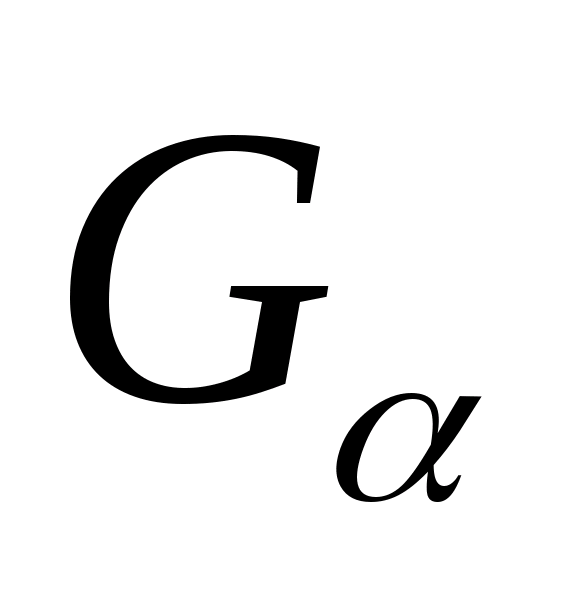 =
(X
\
=
(X
\
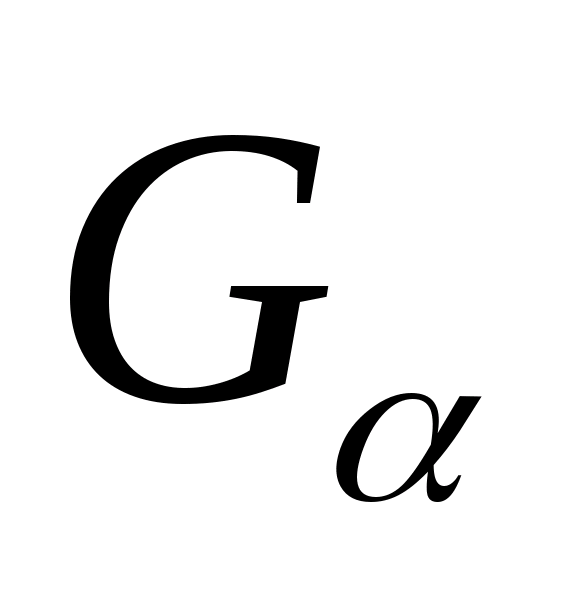 ),
),
несложно доказывается следующая теорема.
Теорема 1. (Свойства замкнутых множеств)
1. Пересечение любой совокупности замкнутых множеств есть замкнутое множество.
2. Объединение любых двух замкнутых множеств есть замкнутое множество.
Доказательство. Пусть для любого определено множество
F = X
\
= X
\
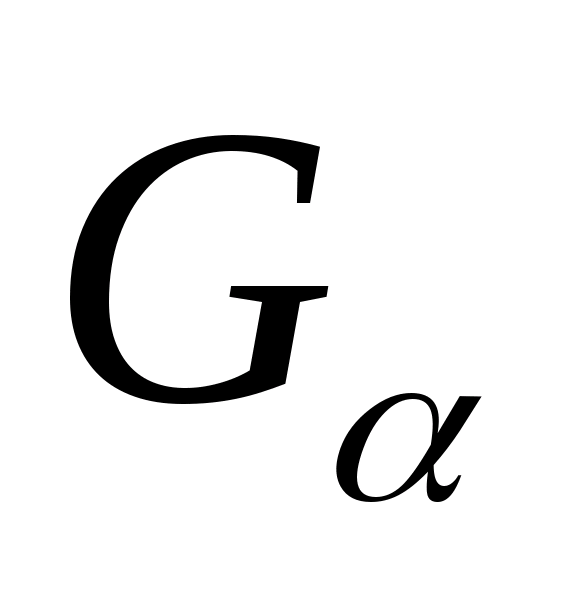 ,
,
где
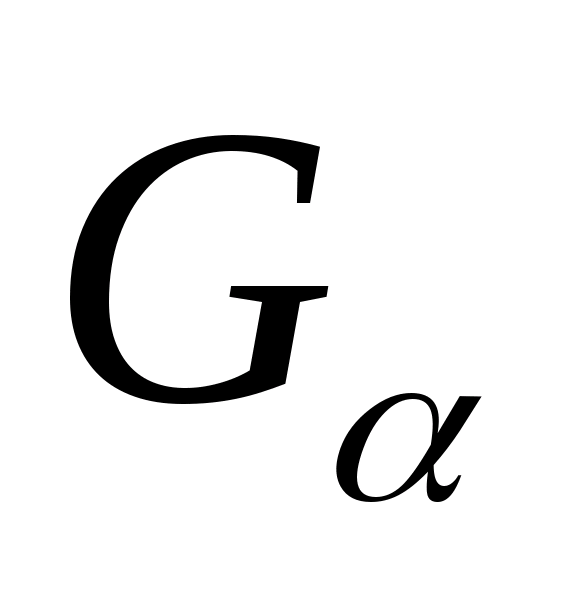 -
открытое множество в (Х, Ф).
-
открытое множество в (Х, Ф).
F>0>
=
F = (X
\
= (X
\
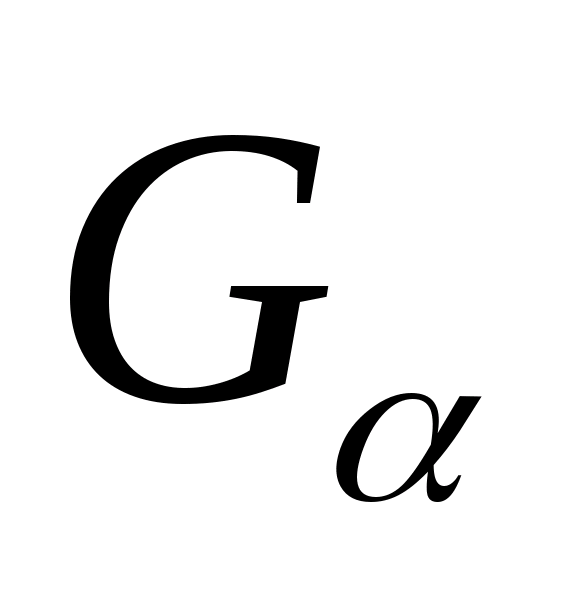 )
= X
\(
)
= X
\(
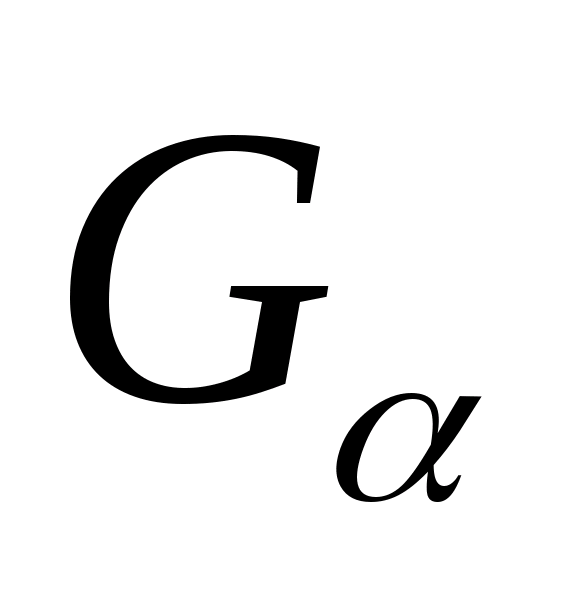 ).
).
Так
как
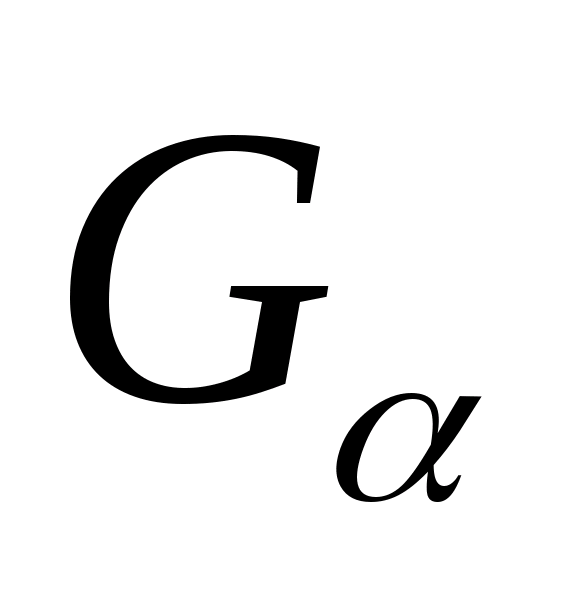 = G>0>
,
то F>0>
– замкнуто.
= G>0>
,
то F>0>
– замкнуто.
F = F>1> F>2> = (X \ G>1>) (X \ G>2>) = X \ (G>1> G>2>).
Так как G>1> G>2> = G , то F – замкнуто.
Теорема 2. Пересечение любого конечного числа открытых множеств является открытым множеством; объединение любого конечного числа замкнутых множеств является замкнутым множеством.
Однако, если в R с обычной топологией рассмотреть множества
G>n>>
>=
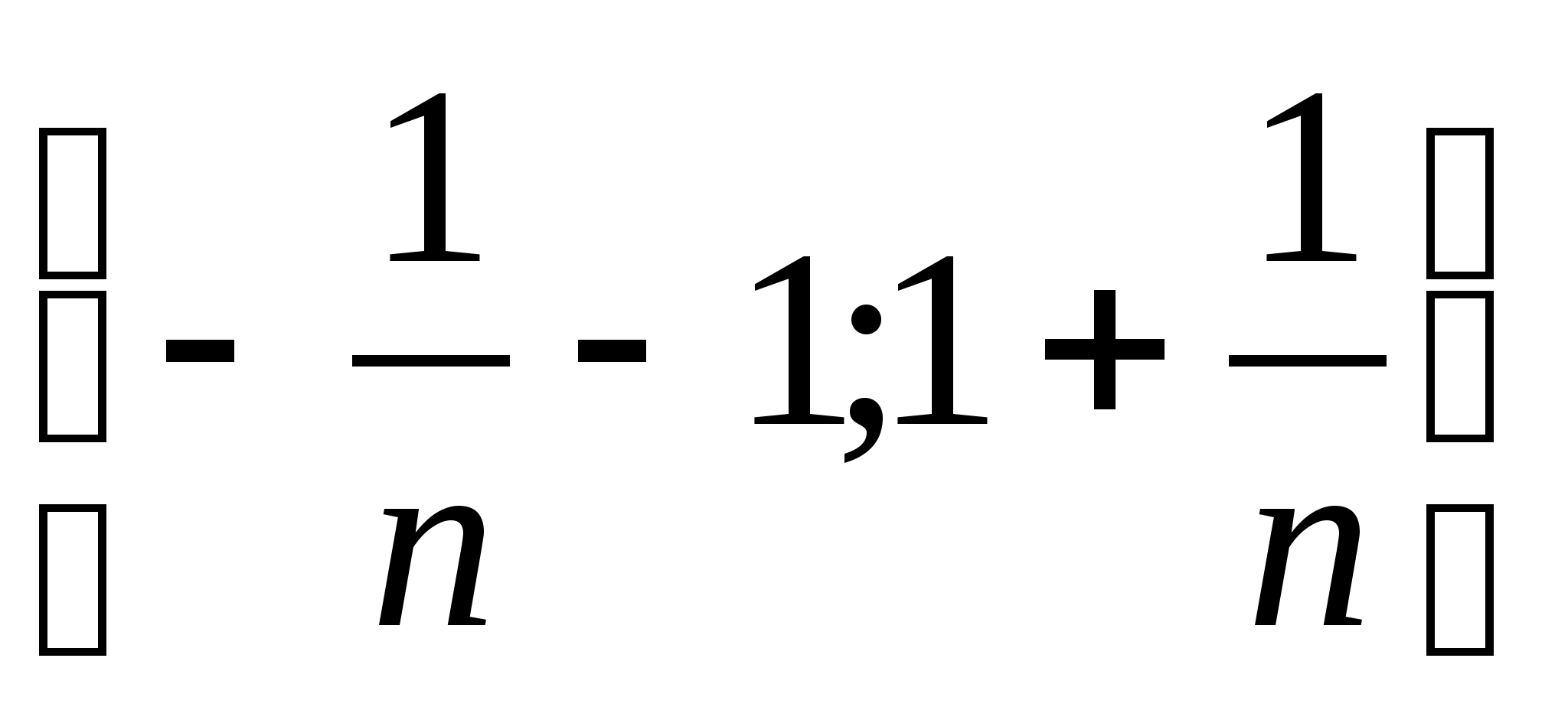 ,
,
то
 G>n>
= –1,
1,
G>n>
= –1,
1,
то есть мы указали пример, когда пересечение бесконечного множества открытых множеств оказалось замкнутым.
Пусть (Х, Ф) – топологическое пространство. Открытое множество U называется окрестностью точки х если х U (х X и U Ф).
Определение
2.
Точка
 называется внутренней точкой некоторого
множества H
(H
X),
если существует такая окрестность U
точки
называется внутренней точкой некоторого
множества H
(H
X),
если существует такая окрестность U
точки
 ,
что U
H.
Множество всех внутренних точек множества
H
обозначается через int
H
и называется внутренней областью H
или внутренностью H.
,
что U
H.
Множество всех внутренних точек множества
H
обозначается через int
H
и называется внутренней областью H
или внутренностью H.
Определение
3.
Точка
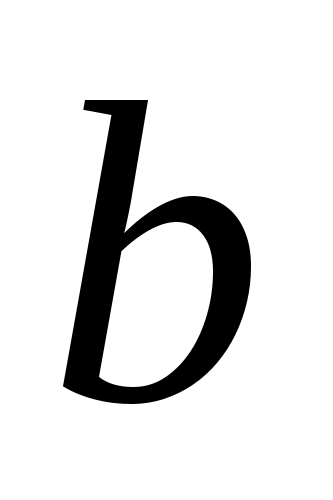 называется внешней точкой множества
H,
если существует такая окрестность V
точки
называется внешней точкой множества
H,
если существует такая окрестность V
точки
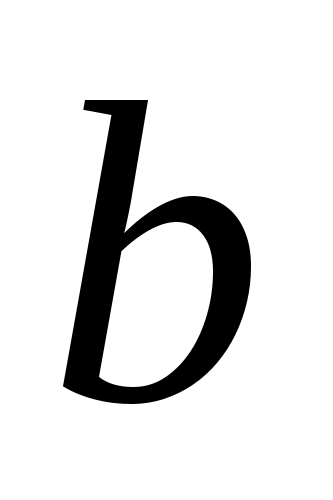 ,
в которой нет точек из H,
т.е. V
С>х>
H=Х
\ H.
Множество всех внешних точек множества
H
обозначается через ext
H
и называется внешней областью H.
,
в которой нет точек из H,
т.е. V
С>х>
H=Х
\ H.
Множество всех внешних точек множества
H
обозначается через ext
H
и называется внешней областью H.
Определение 4. Точка с называется граничной для множеств H, если в любой окрестности точки с имеются как точки множества H, так и точки не принадлежащие H.
Множество
всех граничных точек множества H
обозначается через
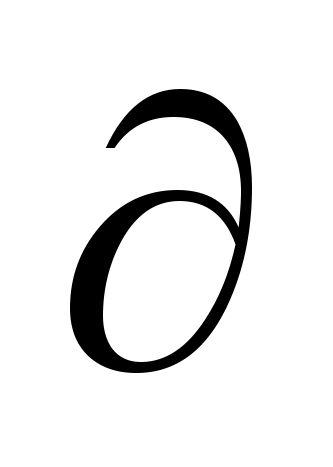 H
и называется границей H.
H
и называется границей H.
Очевидно:
int
H
ext H
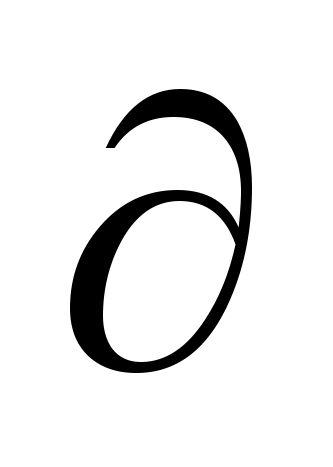 H
= X
H
= X
int
H
ext H = ext H
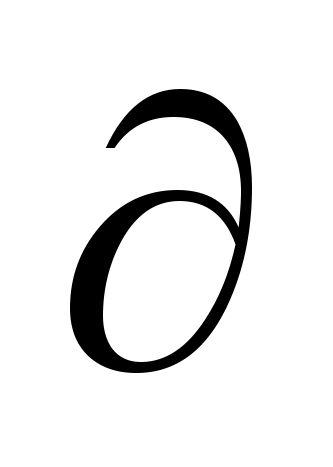 H
= int
H
= int
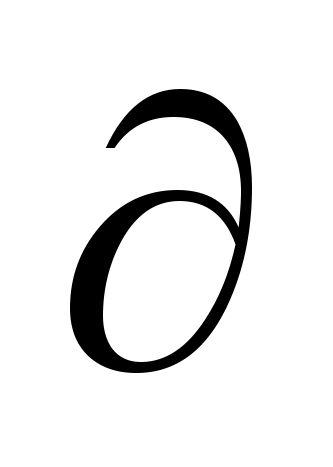 H
=
H
=
int H = ext C>x> H, ext H = int C>x> H
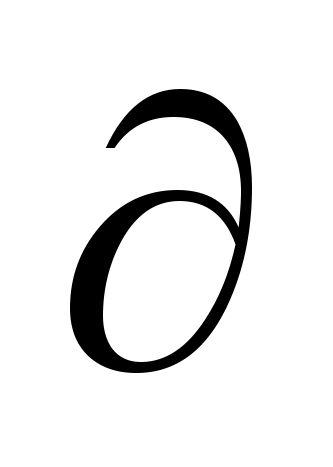 H
=
H
=
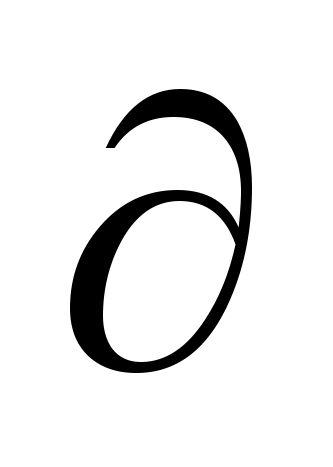 C>x>
H
C>x>
H
Определение
5.
Точка
 называется точкой прикосновения
множества H,
если каждая окрестность точки
называется точкой прикосновения
множества H,
если каждая окрестность точки
 имеет с H
хотя бы одну общую точку.
имеет с H
хотя бы одну общую точку.
Множество
всех точек прикосновения множества H
называется замыканием множества H
и обозначается
 .
Ясно, что
.
Ясно, что
 = int
H
= int
H
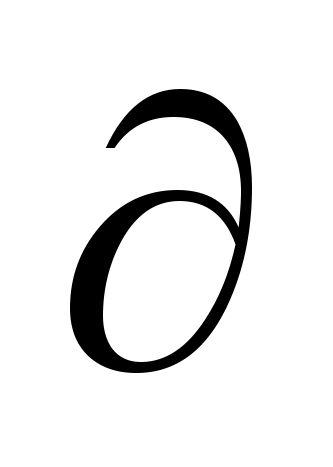 H
и является замкнутым множеством.
H
и является замкнутым множеством.
Определение
6.
Точка

H
называется изолированной точкой
множества H,
если существует окрестность U
точки
H
называется изолированной точкой
множества H,
если существует окрестность U
точки
 ,
такая, что
,
такая, что
U H =
Определение
7.
Если

 и не является изолированной для H,
то она называется предельной точкой
множества H.
и не является изолированной для H,
то она называется предельной точкой
множества H.
Ясно,
что в каждой окрестности предельной
точки

H
существуют точки множества H,
отличные от
H
существуют точки множества H,
отличные от
 .
.
Поскольку замыкание распадается на множество изолированных и предельных точек, а первое всегда содержится в H, то приходим к следующему утверждению:
Теорема 3. Множество H замкнуто тогда и только тогда, когда оно содержит все свои предельные точки, то есть, если
H
=
Действительно, если H – замкнуто, то C H = X \ H открыто. Поэтому C H = ext H.
Отсюда получаем
H
= int
H
∂ H
=
 .
.
Теорема
4.
Если замкнутое множество F
содержит множество H,
то F
содержит и
 .
.
Доказательство. Так как H F, то все предельные точки H будут являться предельными и для F, а поэтому они принадлежат F, следовательно
 F.
F.
Следствие. Замыкание множеств H есть пересечение всех замкнутых множеств, содержащих H.
Действительно,
согласно теореме 5
 принадлежит любому замкнутому множеству,
содержащему H,
а по теореме 3
принадлежит любому замкнутому множеству,
содержащему H,
а по теореме 3
 -
замкнутое множество.
-
замкнутое множество.
Определение
8.
Множество H
называется всюду плотным в топологическом
пространстве (Х, Ф), если
 = X.
= X.
Множество
А называется нигде не плотным в
пространстве (Х, Ф), если дополнение к
замыканию А всюду плотно в Х, то есть
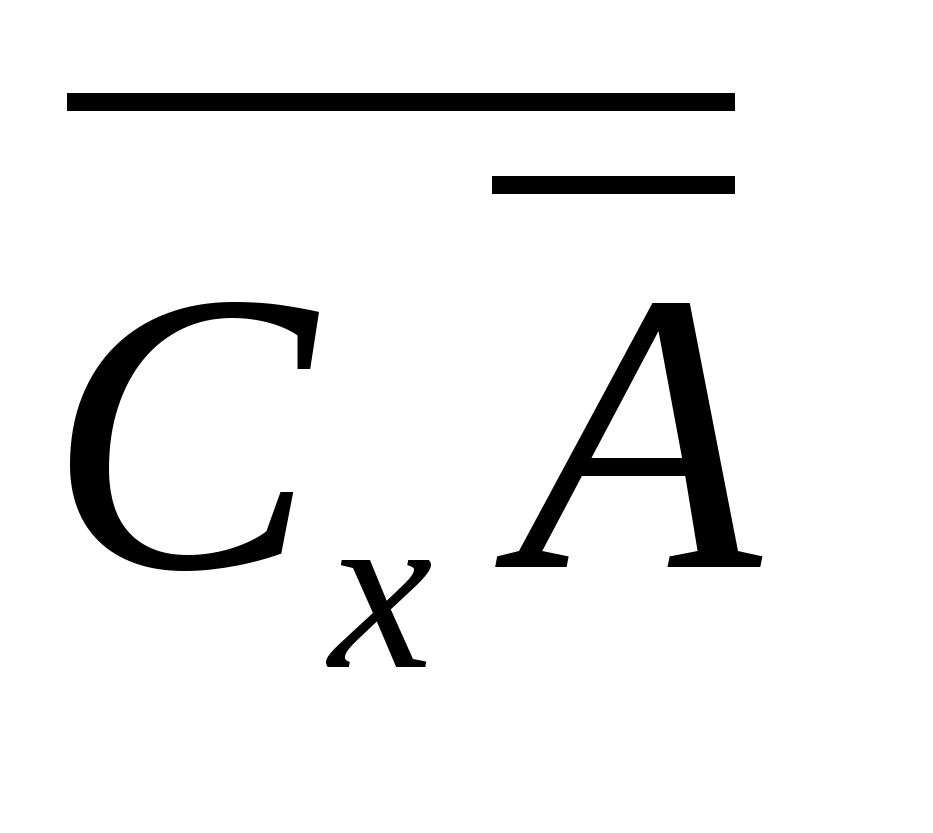 =
Х
=
Х
1.2.3 Базис и отделимость топологического пространства
Определение
1.
Пусть (Х, Ф) – топологическое пространство,
и пусть G*
=G
– некоторое семейство открытых множеств
в этом пространстве. Если любое открытое
множество в (Х, Ф) представимо в виде
объединения некоторых множеств G*,
то G*
называется базисом топологического
пространства (Х, Ф) или базой.
– некоторое семейство открытых множеств
в этом пространстве. Если любое открытое
множество в (Х, Ф) представимо в виде
объединения некоторых множеств G*,
то G*
называется базисом топологического
пространства (Х, Ф) или базой.
Теорема
1.
Для того, чтобы семейство G*
=G
было базисом топологического пространства
(Х, Ф) необходимо и достаточно, чтобы для
любой точки
было базисом топологического пространства
(Х, Ф) необходимо и достаточно, чтобы для
любой точки

Х и любой её окрестности U>a>
существовало множество G>>>
Х и любой её окрестности U>a>
существовало множество G>>>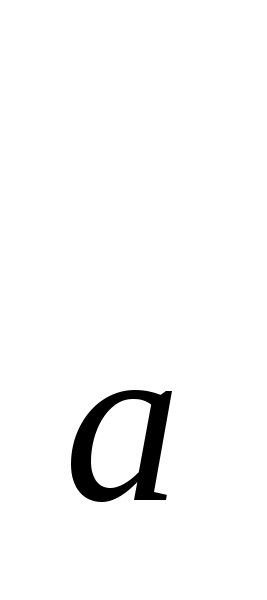 >
G*
такое, что
>
G*
такое, что

G>>>
G>>>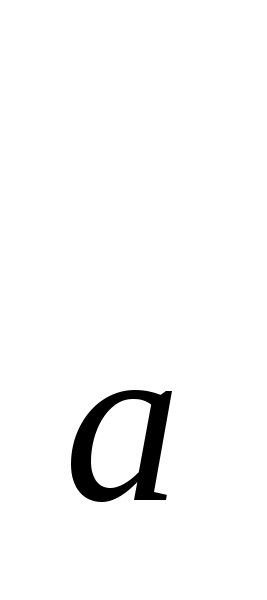 >
и G>>>
>
и G>>>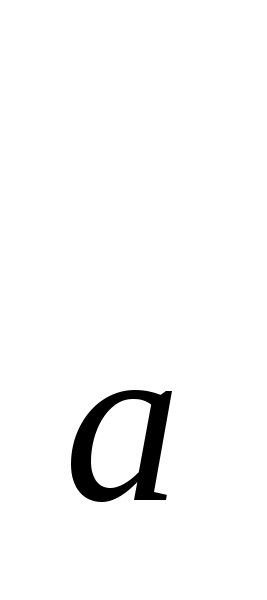 >
U>a>>.>
>
U>a>>.>
Теорема
2.
Для того, чтобы семейство подмножеств
G*
= G
было базисом некоторого топологического
пространства Х необходимо и достаточно,
чтобы для любых двух элементов U>,>
V
G*
и каждой точки х
U
V
существовал такой элемент W
G*,
что х
W
и W
U
V.
При этом
G*
и
было базисом некоторого топологического
пространства Х необходимо и достаточно,
чтобы для любых двух элементов U>,>
V
G*
и каждой точки х
U
V
существовал такой элемент W
G*,
что х
W
и W
U
V.
При этом
G*
и
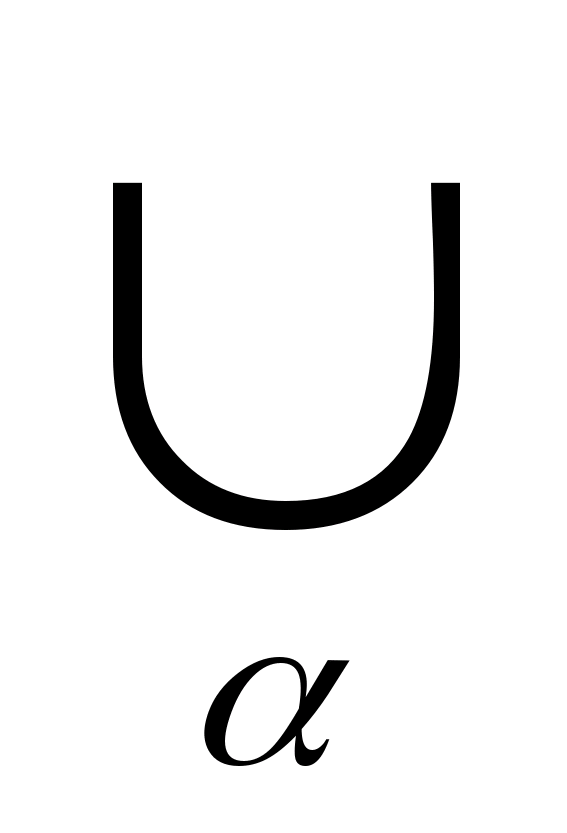 G
G = X.
= X.
Доказательство. 1. Пусть G* – база. Тогда, так как U V – открытое множество, то согласно теореме 1 существует W такое, что W G* и х W U V.
2. Докажем обратное утверждение. Пусть G* – семейство с выделенными нами специальными свойствами. В-семейство всевозможных объединений элементов из G*. Покажем, что В-топология. Ясно, что объединение любой совокупности элементов из В является объединением элементов из G*, а, следовательно, принадлежит В.
Пересечение любых двух элементов U и V из В также принадлежит В.
Действительно, если х>0> U V, то существует U G* и V G* такие, что U U, V V и х>0> U V. Тогда по условию существует
W G*, для которого
х>0> W U V U V.
Но, тогда
U
V
=

В.
В.
Кроме того,
Х
=
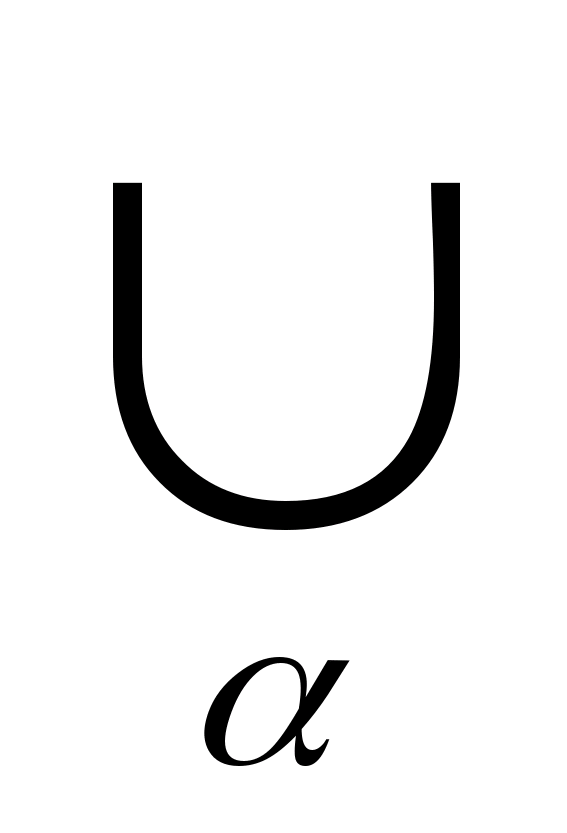 G
G
В.
В.
Итак, В-топология, а G* её базис.
Теорема доказана.
Из предыдущих теорем следует, что не всякое семейство G* может служить базой топологии. Возникает вопрос: можно ли по произвольному семейству G>i> множеств определить некоторую топологию? Эта топология должна быть определена на множестве Х, являющимся объединением всех элементов G>i>, каждый элемент из G>i> должен быть открыт в этой топологии.
Кроме того, возникает вопрос: существует ли наименьшая топология на Х, содержащая G>i>? На этот вопрос отвечает следующая теорема.
Теорема
3.
Пусть G*
= G>i>
– произвольное непустое семейство
множеств. Тогда семейство всевозможных
конечных пересечений элементов из G*
образует базу некоторой топологии на
множестве Х =
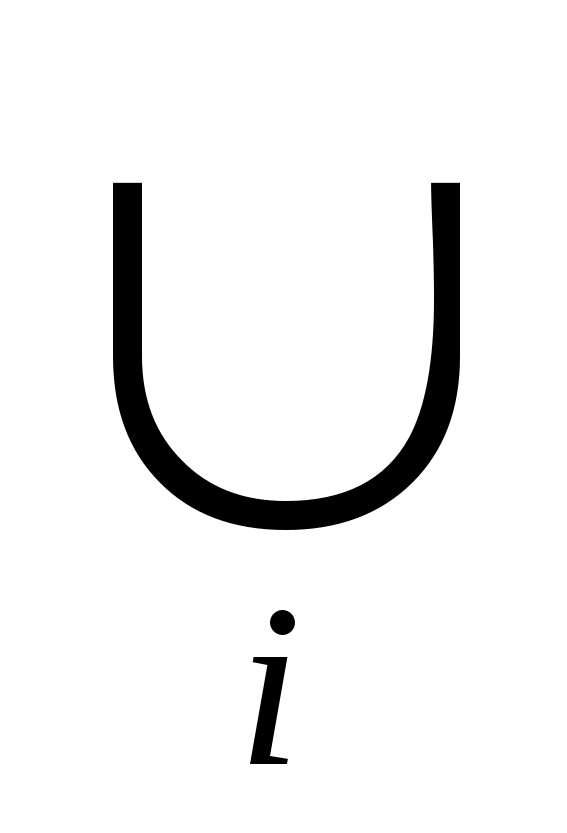 G>i>.
G>i>.
Доказательство. Обозначим В-семейство всевозможных конечных пересечений элементов из G*. Тогда пересечение любых двух элементов из В снова является элементом В. В силу теоремы 2 получим, что В-база некоторой топологии.
Теорема доказана.
У пространств, топология которых обладает счетной базой, есть много хороших свойств.
Примеры. 1. В любом топологическом пространстве (Х, Ф) множество Ф – база (очевидно).
2.
(R,
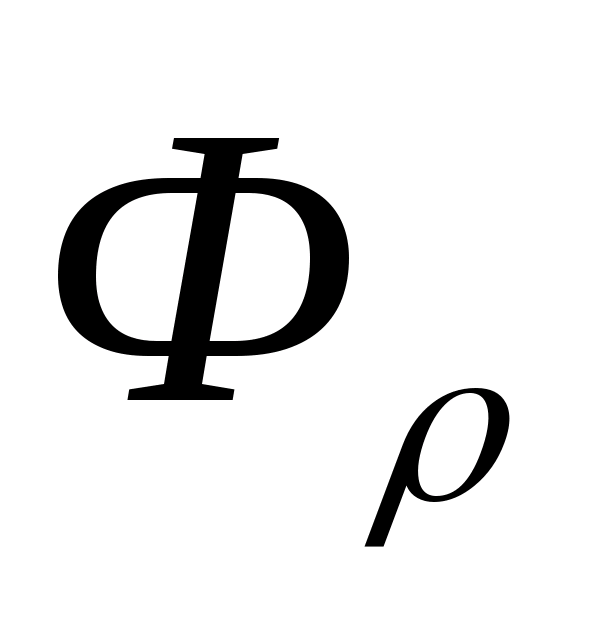 ),
),
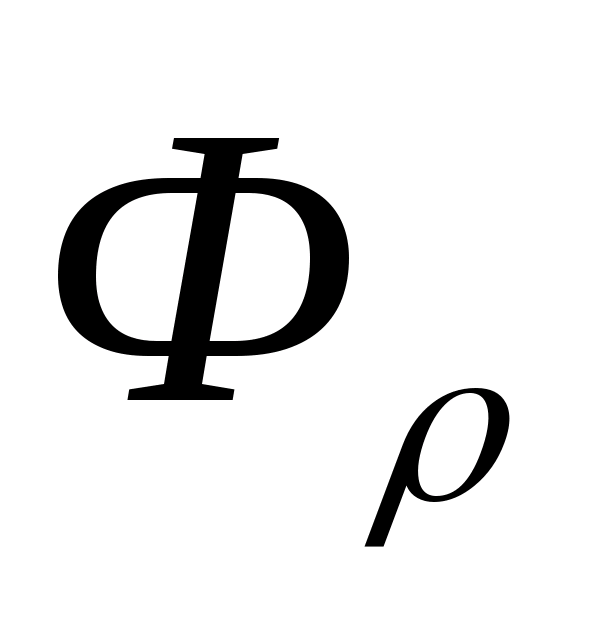 – топология, заданная метрикой.
– топология, заданная метрикой.
G* = , всевозможные интервалы – база.
3. (Х. Ф) дискретная топология.
G* = } {х| х Х – база.
Аксиома отделимости
Наличие хороших свойств пространства зависит от возможности отделить одну точку от другой с помощью окрестностей этих точек.
Поэтому, обычно, рассматривают такие топологические пространства, которые удовлетворяют дополнительным условиям, например, так называемым аксиомам отделимости.
Аксиома Хаусдорфа
Для любых двух различных точек пространства существуют их непересекающиеся окрестности.
Топологические пространства, в которых выполняется аксиома Хаусдорфа, называют хаусдорфовыми пространствами.
Нетрудно доказать, что любое подпространство хаусдорфова пространства, содержащее не менее двух различных точек, также является хаусдорфовым пространством.
В любом топологическом пространстве можно рассмотреть сходящуюся последовательность точек.
Однако, понятие предела удобно лишь там, где сходящаяся последовательность имеет единственный предел.
Оказывается, аксиома 2 является необходимым и достаточным условием единственности предела сходящейся последовательности.
Пусть в топологическом пространстве (Х, Ф) дана последовательность точек х>1>, х>2>, …, х>n>, … точка х>0> называется пределом этой последовательности, если для любой окрестности U>x>>0> точки х>0> найдётся такой номер n>0>, что для всех n n>0> точки х>n> U>x>>0>.
При этом последовательность точек х>n> называется сходящейся к точке х>0>.
Теорема 4. В хаусдорфовом пространстве (Х, Ф) сходящаяся последовательность точек х>n> имеет единственный предел.
Пример 1. В силу теоремы 2 § 1 любое топологическое пространство, топология которого порождена метрикой, является хаусдорфовым пространством.
Пример 2. Двуточечное топологическое пространство
Х
=
 ,
Ф = {,
Х,
,
Ф = {,
Х,
 }
}
не является хаусдорфовым пространством.
Действительно,
рассмотрим точки
 и
и
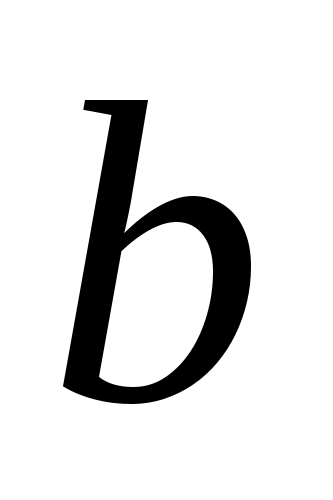 .
Для них нет непересекающихся окрестностей,
так как окрестностью точки
.
Для них нет непересекающихся окрестностей,
так как окрестностью точки
 является сама точка
является сама точка
 или все Х, а окрестностью точки
или все Х, а окрестностью точки
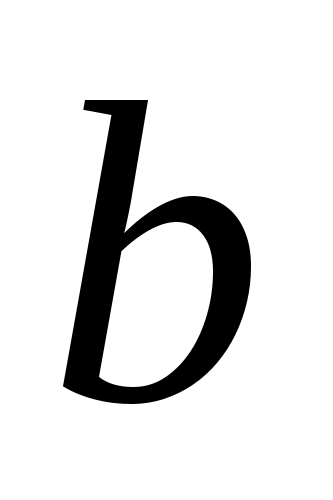 будет только Х.
будет только Х.
Очевидно,

Х =
Х =
 и предложение доказано.
и предложение доказано.
1.2.4 Компактность топологических пространств
Определение 1. Пусть (Х, Ф) – топологическое пространство и множество Н Х. Семейство U = А>> открытых множеств А>> называется открытым покрытием множества Н, если
Н
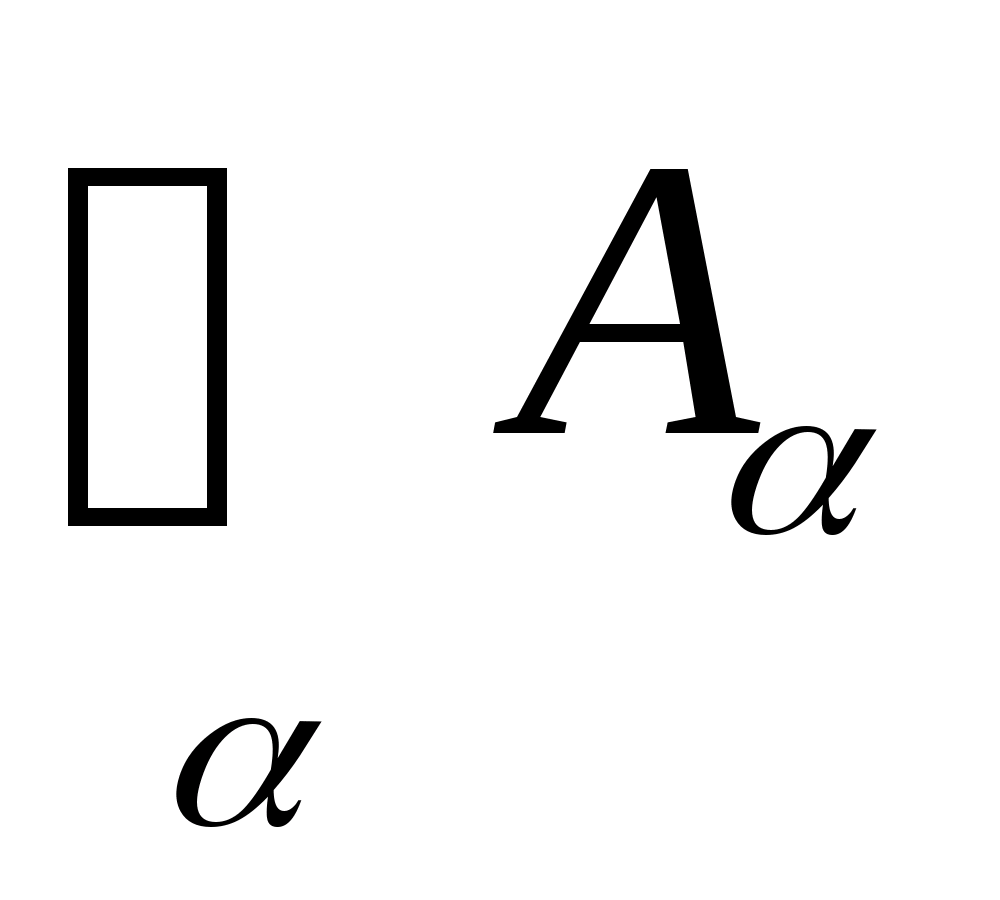 .
.
Подпокрытие покрытия U – это такое подсемейство семейства U, которое само является покрытием для Н.
Определение 2. Топологическое пространство Х называется компактным или компактом, если из любого его открытого покрытия можно выбрать конечное подпокрытие.
Определение 3. Множество М в топологическом пространстве Х называется компактным, если оно является компактным топологическим пространством относительно индуцированной топологии (как подпространство).
Пользоваться этим определением компактности множества не очень удобно, так как оно требует построения в множестве с индуцированной топологией. Следующая теорема дает нам возможность обходиться без этих дополнительных построений.
Теорема 1. Для того, чтобы множество М в топологическом пространстве Х было компактно, необходимо и достаточно, чтобы из любого открытого покрытия множества М в Х можно было выделить конечное подпокрытие.
Теорема 2. Если топологическое пространство (Х, Ф) компактно, а множество F X – замкнуто, то F – компактно.
Доказательство. Пусть U – произвольное открытое покрытие F. Добавим к U открытое множество (Х \ F).
Тогда система U, (X \ F) – открытое покрытие Х.
Так как Х – компактно, то из полученного выше покрытия выбираем конечное покрытие Х.
Обозначим его U>1>. Если U>1> содержит X \ F, то удалив из U>1> множество X \ F, получим покрытие, причём конечное, для F. Если U>1> не содержит X \ F, то U>1> и является конечным покрытием F.
В силу теоремы 1 множество F – компактно.
Теорема доказана.
Теорема 3. В хаусдорфовом пространстве (Х, Ф) у любых двух компактных непересекающихся множеств имеются непересекающиеся окрестности.
В общем случае мы рассматриваем для каждой точки х В непересекающиеся окрестности множества А – U >x> и точки х – V >x> и выделяем из полученного покрытия множества В окрестностями V >x> конечное покрытие
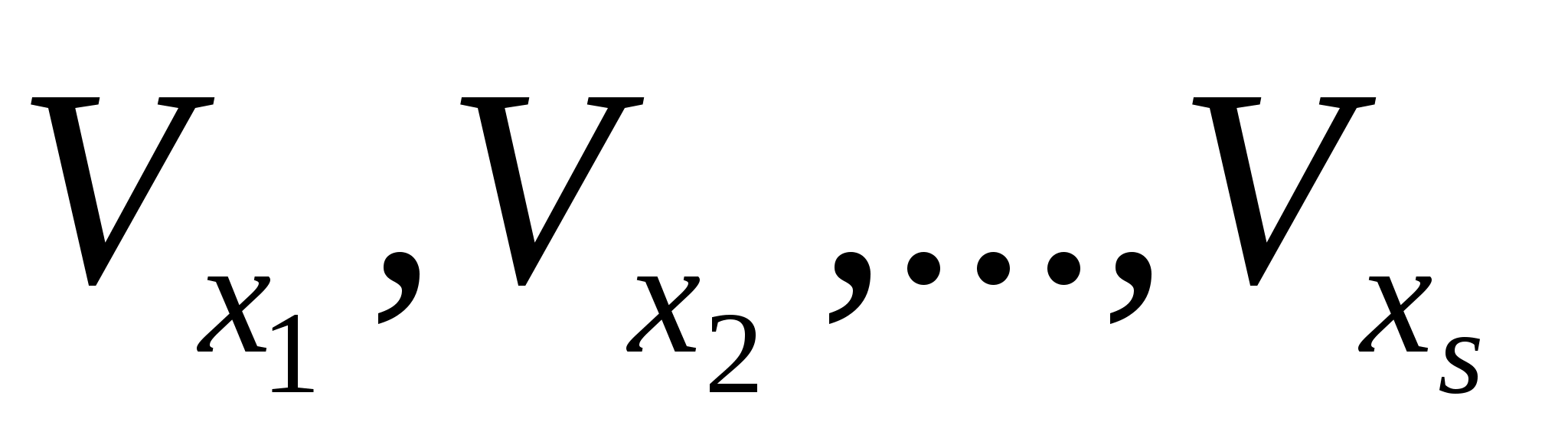 .
.
Множества
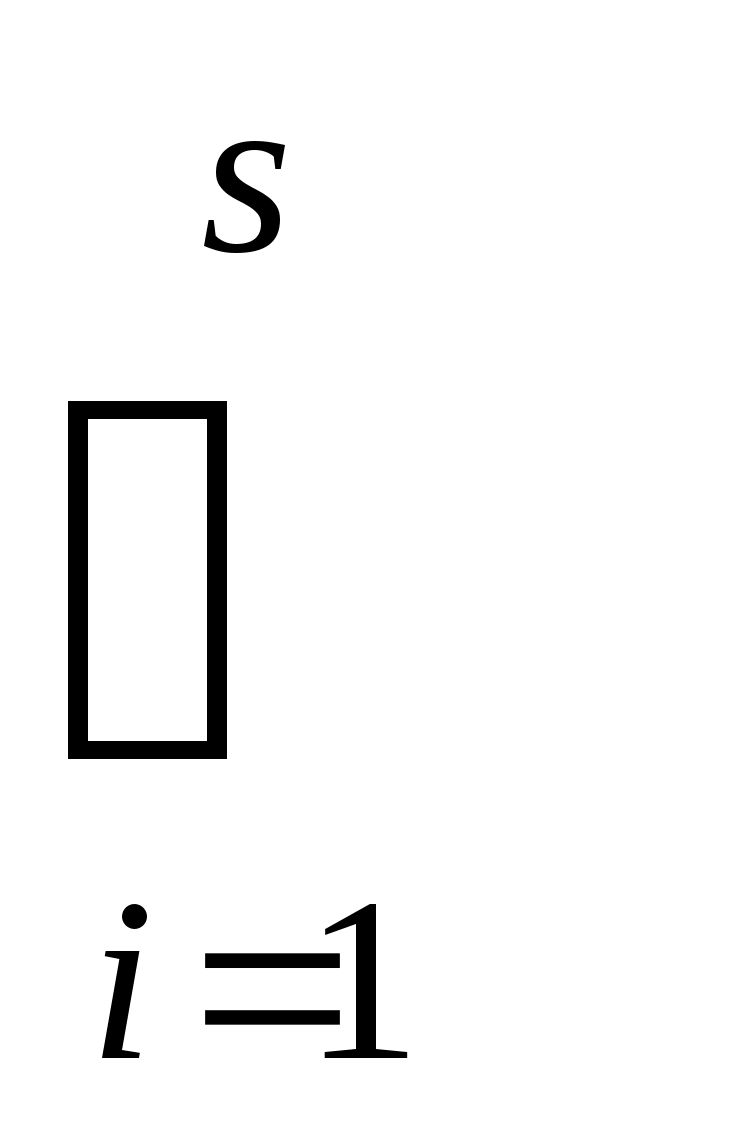
 и
и
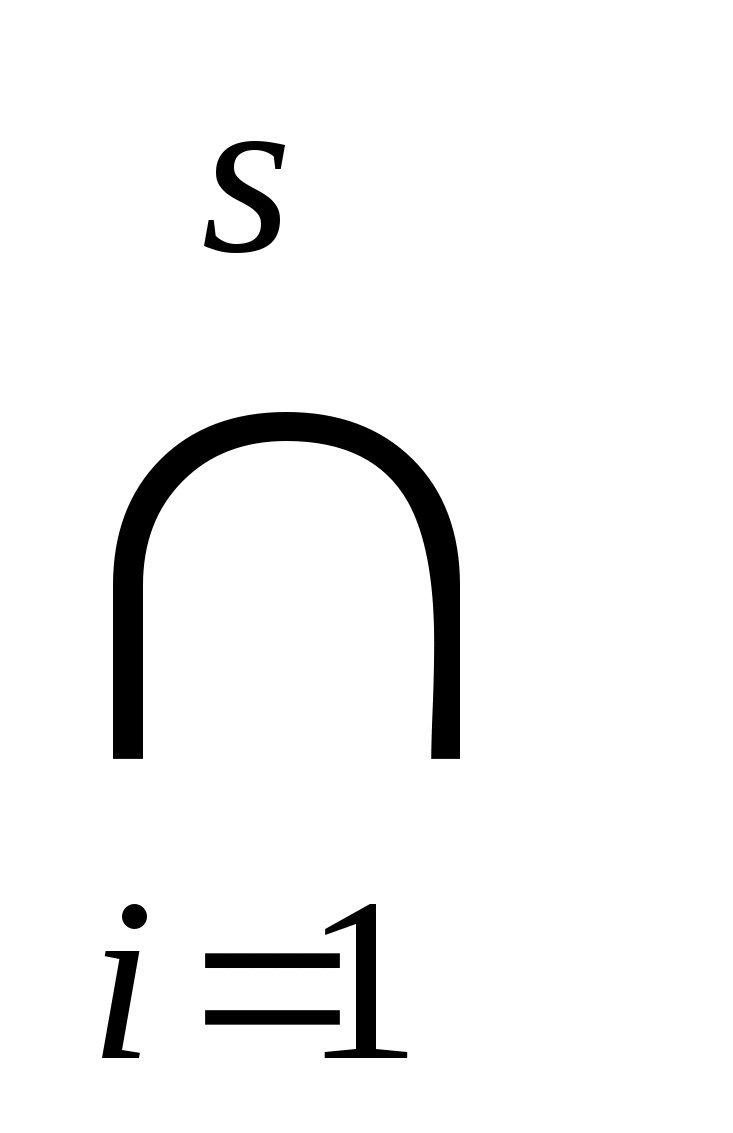
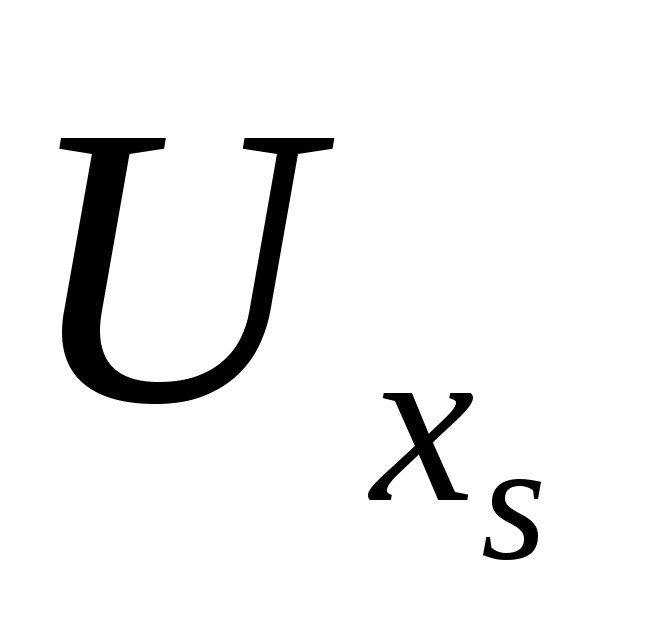
будут непересекающимися окрестностями множеств А и В.
Теорема 4. Компактное подмножество М хаусдорфова пространства (Х, Ф) замкнуто.
Теорема 5. Подмножество в пространстве R3 компактно в том и только том случае, если оно ограничено и замкнуто.
Пример. Доказать, что в евклидовом пространстве с естественной топологией (Е3, Ф>>>)> множество Н состоящее из конечного числа точек компактно.
Доказательство. Пусть Н = {х>1>, х>2>, …, х>n>} и {G>>}>>>А> – произвольное открытое покрытие множества Н. По определению покрытия каждая точка х>i> принадлежит хотя бы одному из множеств G>>. Обозначим G>1> одно из множеств множества {G>>}>>>А> содержащее х>1>. Затем обозначим G>2> одно из множеств множества {G>>}>>>А> содержащее х>2 >и так далее, для точки х>n>> >обозначим G>n> одно из множеств множества {G>>}>>>А> содержащее х>n>.
Получили конечный набор открытых множеств G>1>, G>2>, …, G>n> являющийся покрытием множества Н. Согласно теореме 1 множество Н будет компактным множеством.
1.2.5 Связность топологических пространств
Определение 1. Топологическое пространство (Х, Ф) называется несвязным, если существуют два непустых открытых множества U и V таких, что U V = Х и U V = .
Другими словами топологическое пространство (Х, Ф) может быть разбито на два непустых открытых множества, не имеющих между собой общих точек.
Топологическое пространство (Х, Ф) называется связным, если не существует такого разбиения.
Пример.
Х= ( ,
b),
(X,
Ф) – связное топологическое пространство,
если Ф = ,
Х,
,
b),
(X,
Ф) – связное топологическое пространство,
если Ф = ,
Х,

и, если Ф = ,
Х,
и, если Ф = ,
Х,
 ,
b
– то это пример несвязного топологического
пространства.
,
b
– то это пример несвязного топологического
пространства.
Заметим, что если несвязное пространство Х разбито на два непустых открытых множества U и V, U V = , то U = C>x> V и V = C>x> U.
Поэтому U и V – замкнутые множества.
Отсюда получаем необходимые и достаточные условия.
Теорема 1. Топологическое пространство (X, Ф) будет связным тогда и только тогда, когда в нем одновременно открытым и замкнутым множеством являются лишь само пространство или пустое множество.
Определение 2. Множество М в топологическом пространстве называется связным, если оно является связным пространством относительно индуцированной топологии, то есть связно определяемое им подпространство.
Другими словами, множество М в топологическом пространстве Х называется связным, если нельзя найти двух открытых в Х множеств G>1> и G>2> таких, что
(G>1> М) (G>2> М) = М.
(G>1> М) (G>2> М) = .
G>1> М , G>2> М .
Теорема 2. В топологическом пространстве (Х, Ф) замыкание связного множества – связно.
Теорема 3. Если А и В два открытых множества в (Х, Ф), причем
А В =
и непустое связное множество
H A B,
то H A, или H В.
Теорема
4.
Пусть 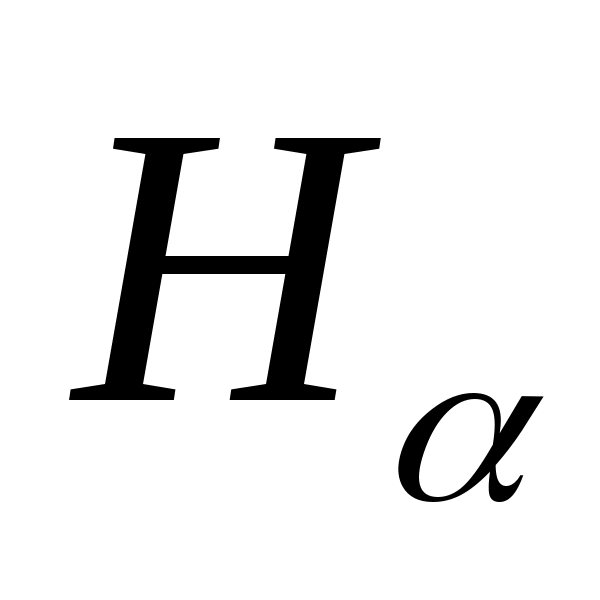
– совокупность связных подмножеств в
пространстве (Х, Ф), имеющих общую точку.
Тогда множество H
=
– совокупность связных подмножеств в
пространстве (Х, Ф), имеющих общую точку.
Тогда множество H
=
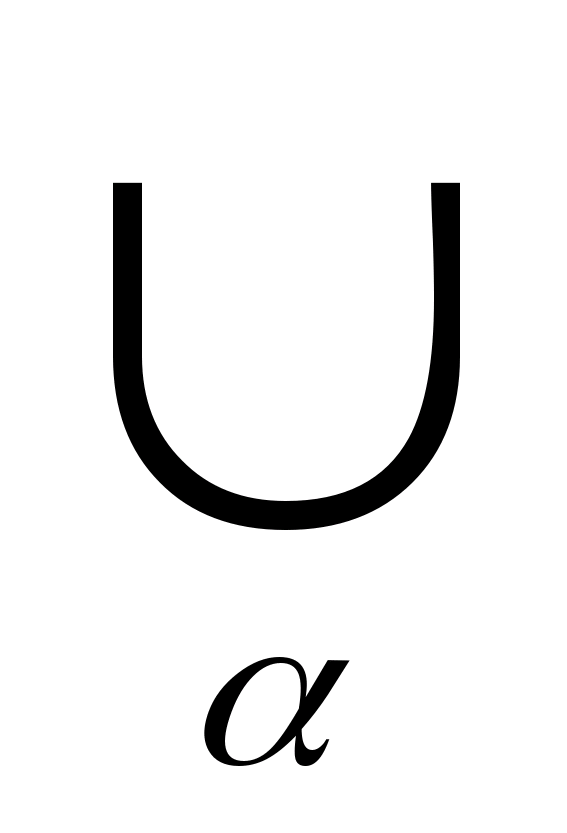
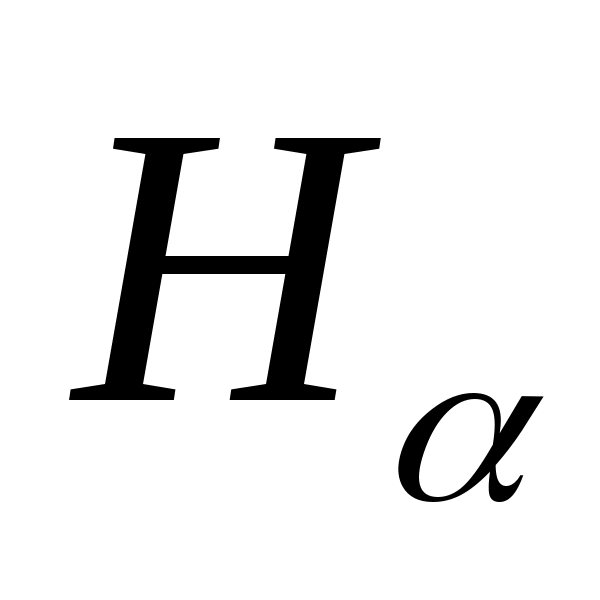 также будет связным в (Х, Ф).
также будет связным в (Х, Ф).
Теорема 5. Компоненты двух различных точек либо не пересекаются, либо совпадают.
Теперь мы можем говорить просто о компонентах пространства, на которые они распадаются.
Теорема 6. Компонента топологического пространства (Х, Ф) является замкнутым множеством.
Доказательство.
Пусть Н – компонента топологического
пространства (Х, Ф), и
 – некоторая ее точка.
– некоторая ее точка.
Очевидно
Н
 ,
,
В
силу теоремы 2 множество
 – связно и так как
– связно и так как

 ,
то
,
то
 Н.
Н.
Поэтому
 =
Н.
=
Н.
Замечание. Пусть топологическое пространство (Х, Ф) – несвязное, то есть существуют два непустых открытых множества U и V таких, что
U V = Х
и
U V = .
Если при этом различные точки х и у принадлежат одной компоненте, то {x, y} U или {x, y} V.
Это утверждение вытекает из теоремы 3.
Определение 3. Областью называется непустое связное открытое множество топологического пространства.
Замкнутой областью называется такое замкнутое множество, которое является замыканием области.
Пример.
Пусть Х – множество действительных
чисел с топологией
 .
Доказать, что любое подмножество
.
Доказать, что любое подмножество
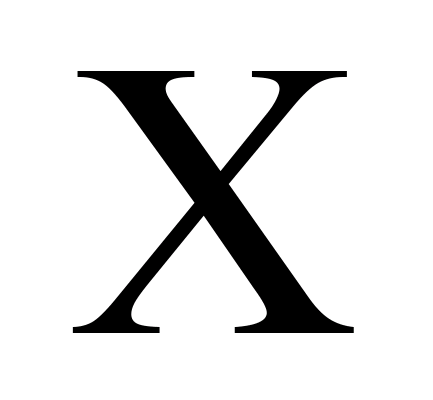 связно.
связно.
Доказательство.
Рассмотрим произвольное подмножество
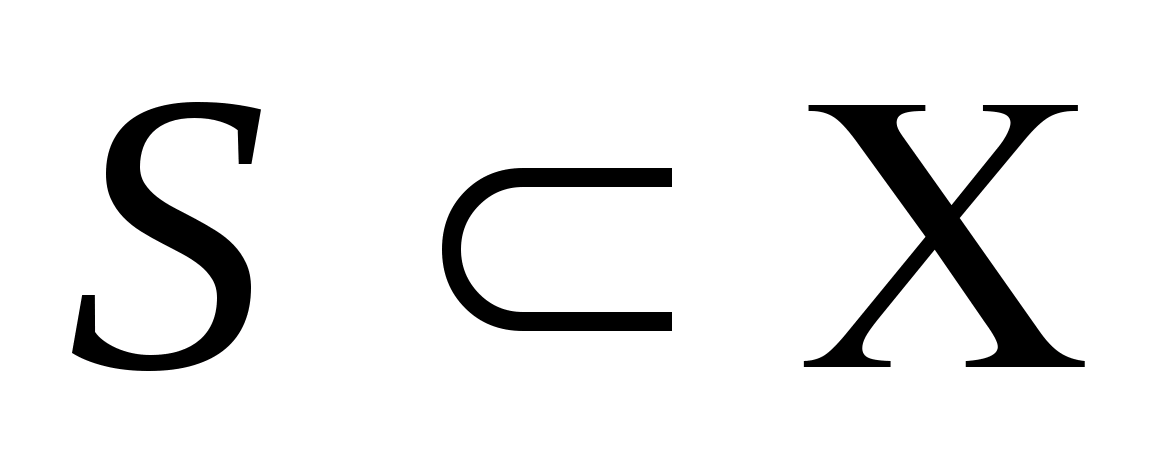 .
Пусть
.
Пусть
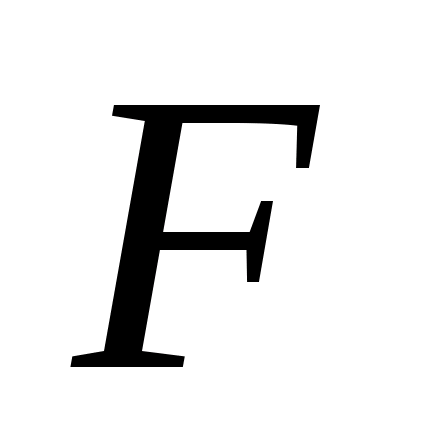 –
непустое подмножество
–
непустое подмножество
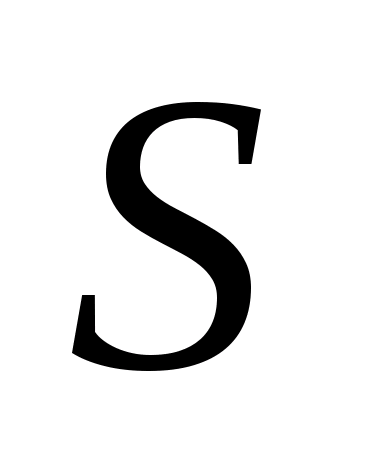 ,
открытое и замкнутое в
,
открытое и замкнутое в
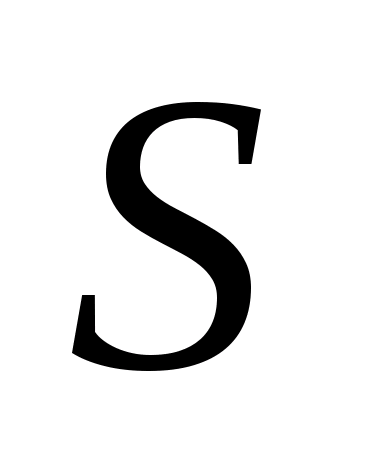 .
Тогда
.
Тогда
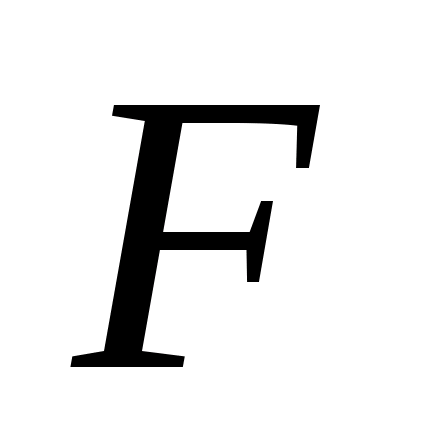 =
=
 ,
,
где
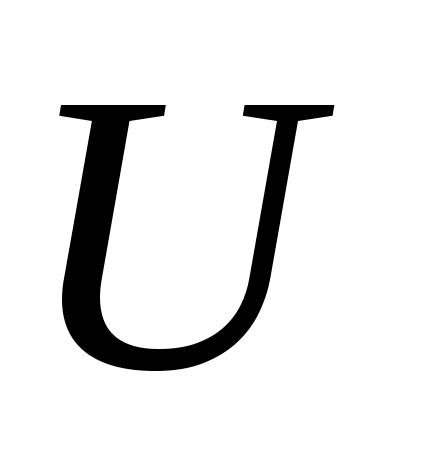 открыто в
открыто в
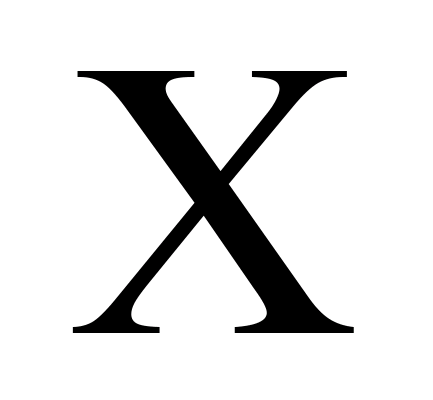 ,
а
,
а
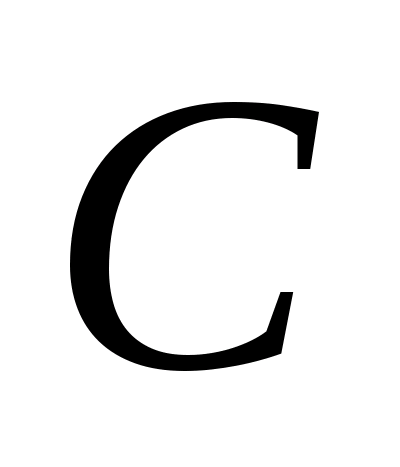 замкнуто в Х, т.е.
замкнуто в Х, т.е.
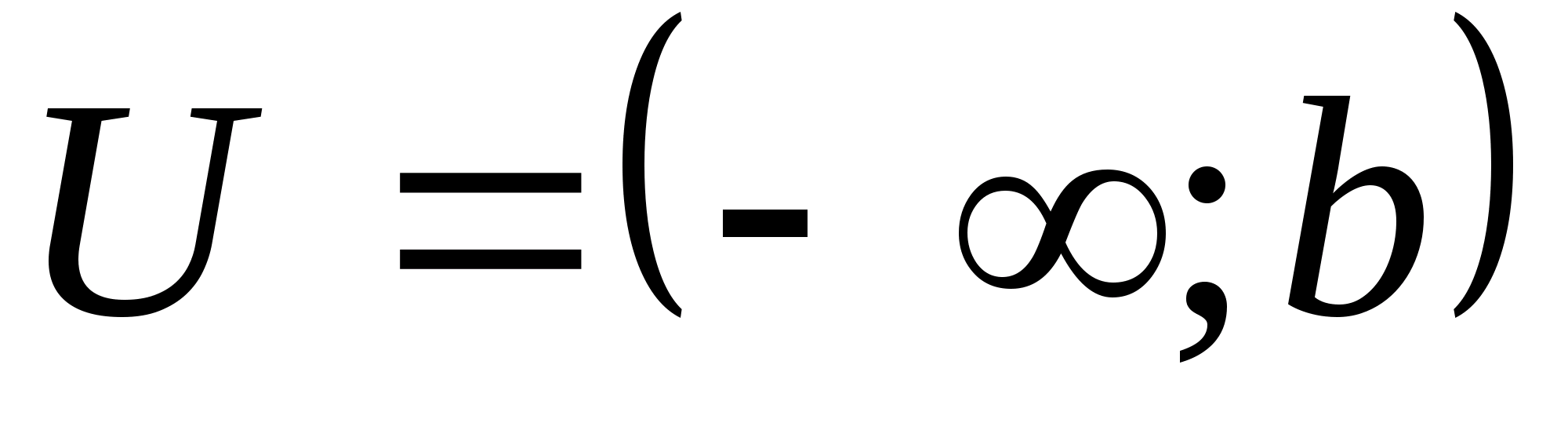 для некоторого
для некоторого
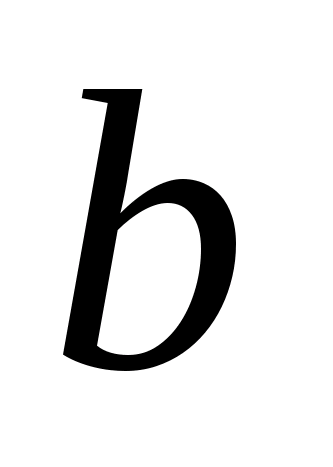 ,
а
,
а
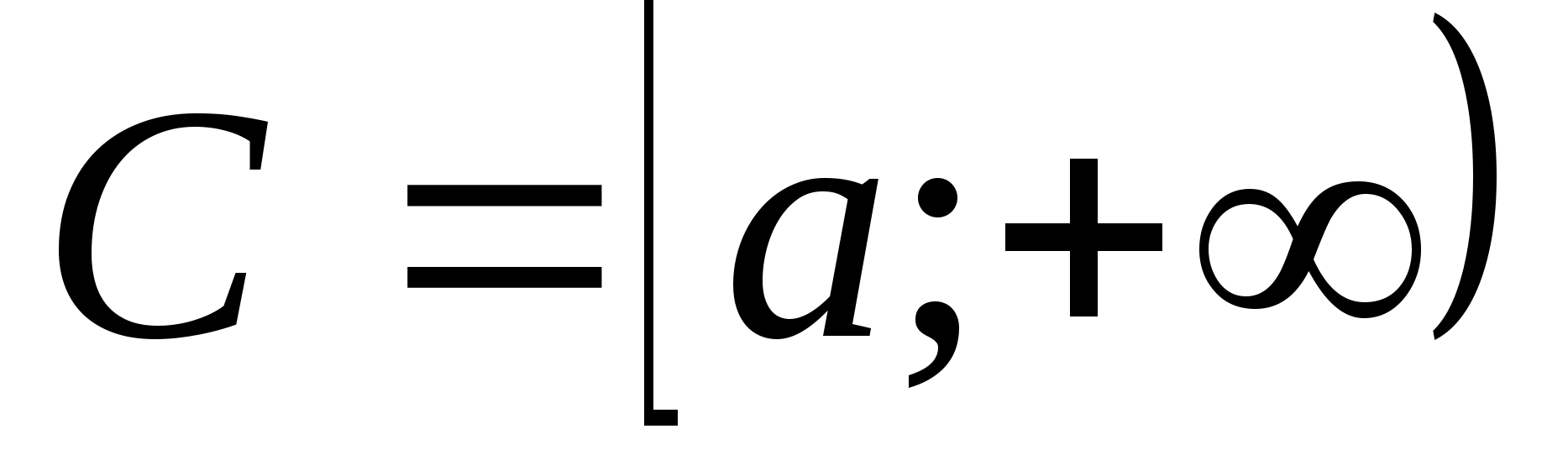 для некоторого
для некоторого
 .
Так как
.
Так как
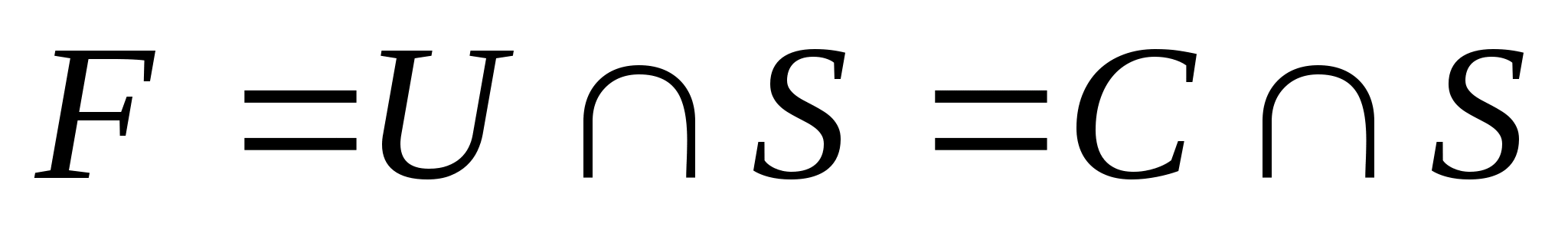 ,
,
то
для любого
 выполнены неравенства
выполнены неравенства
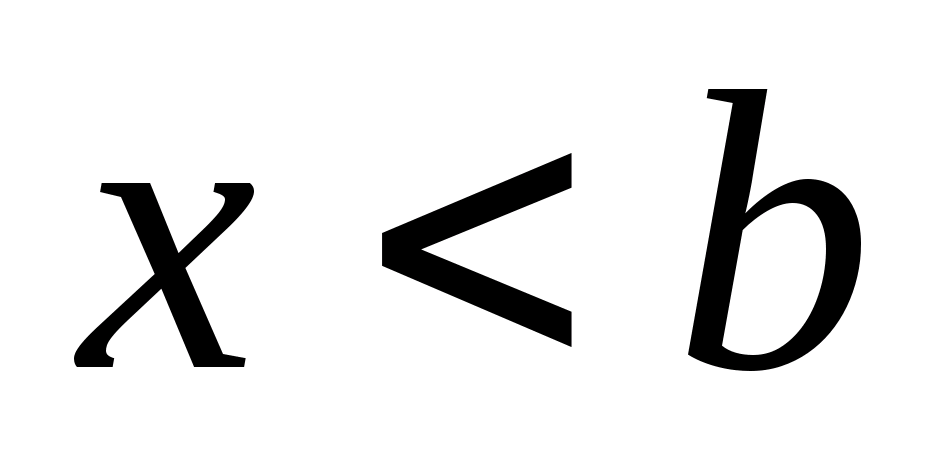 и
и
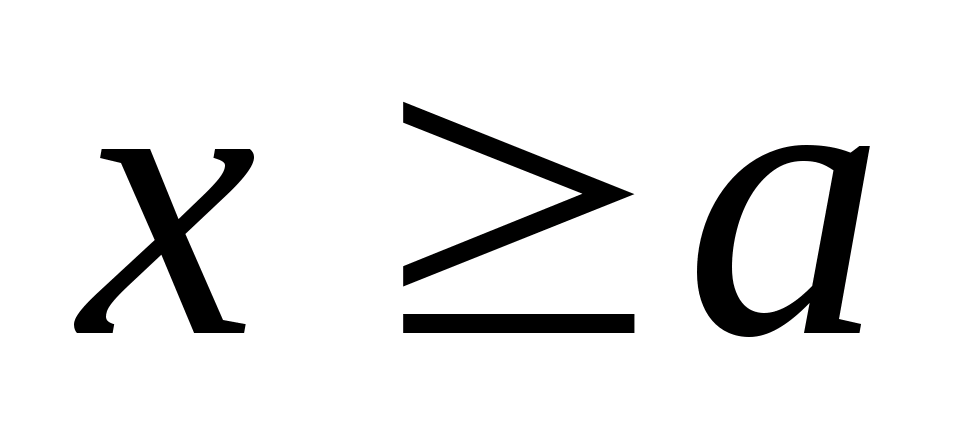 .
.
Действительно,
если найдется значение
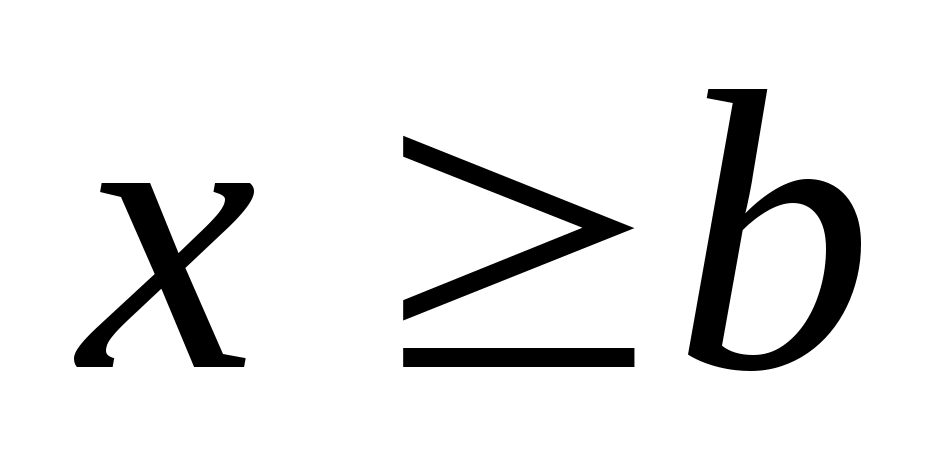 ,
то
,
то
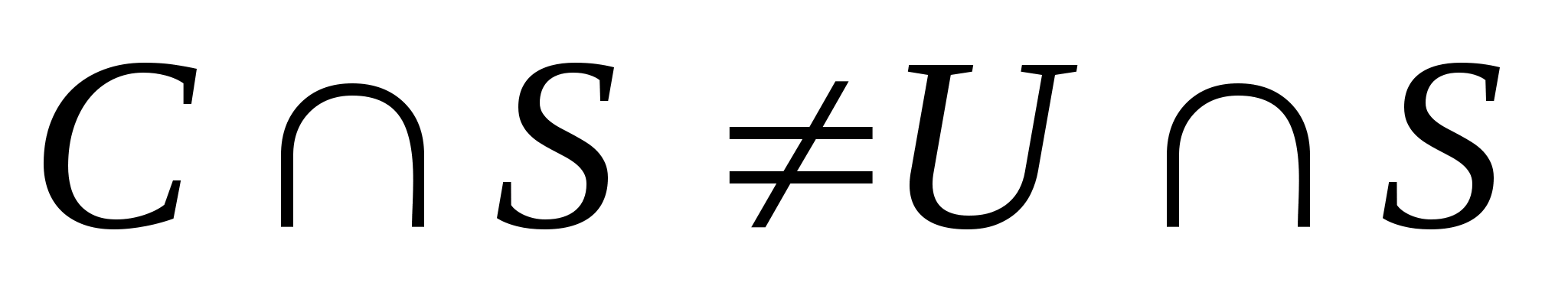 .
Аналогично, если найдется значение
.
Аналогично, если найдется значение
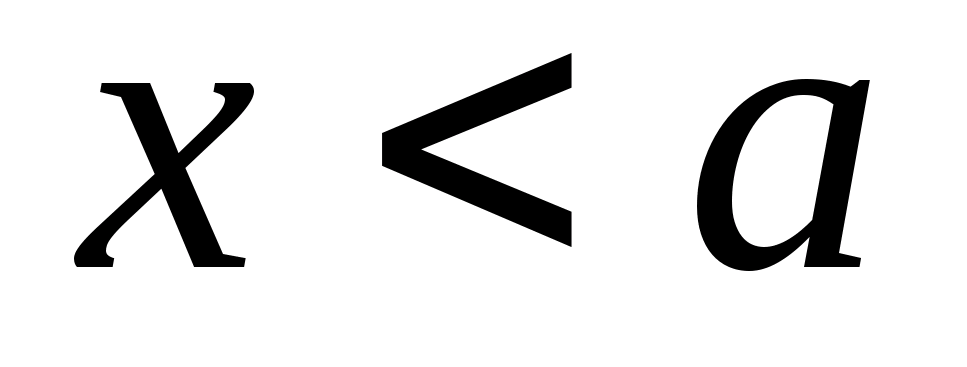 ,
то
,
то
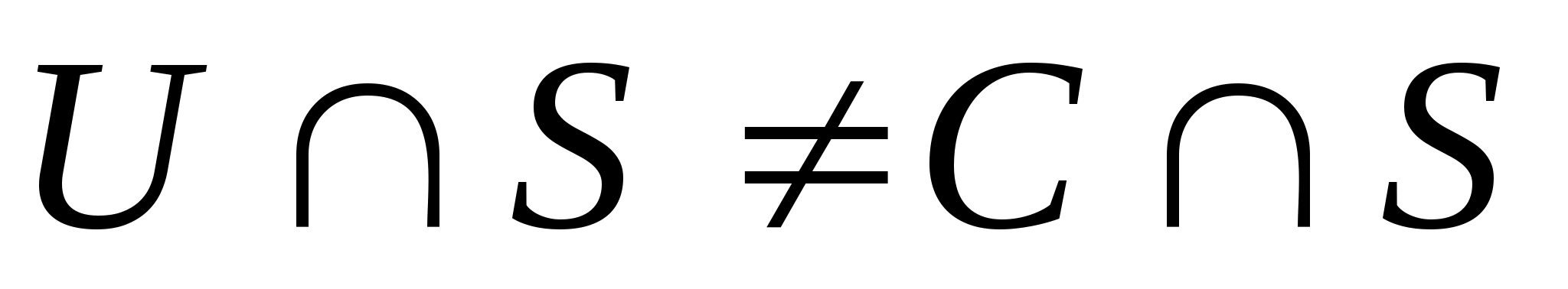 .
.
Итак,
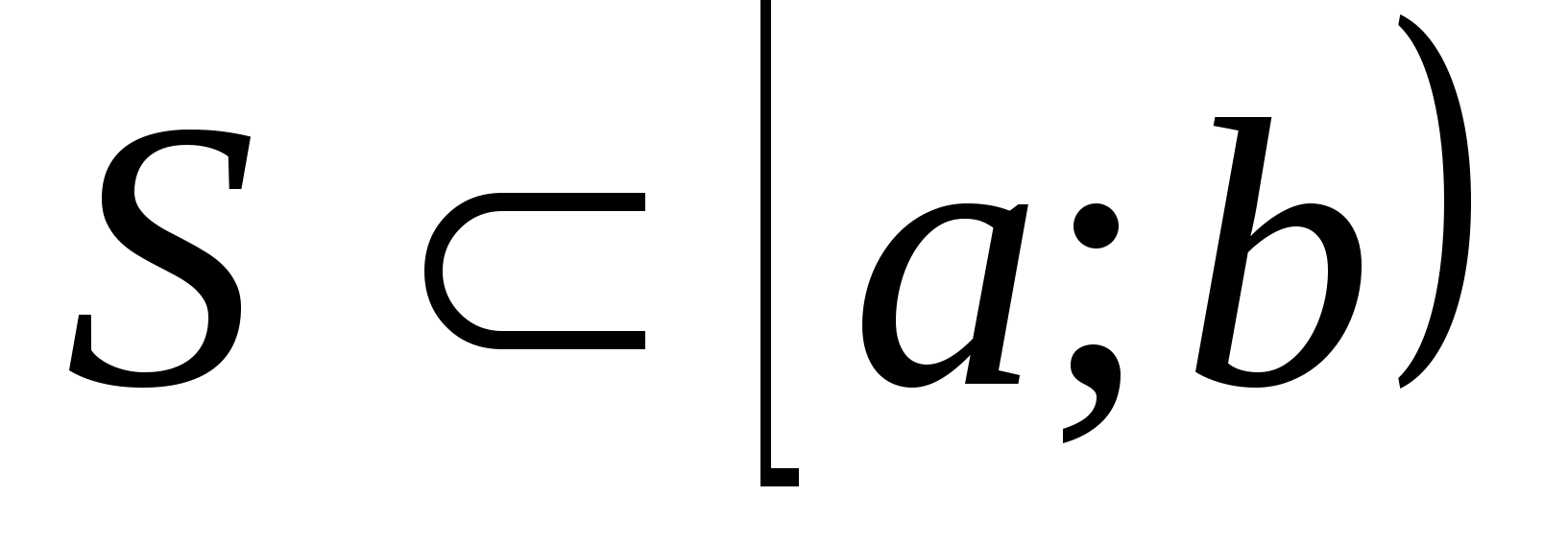 и
и
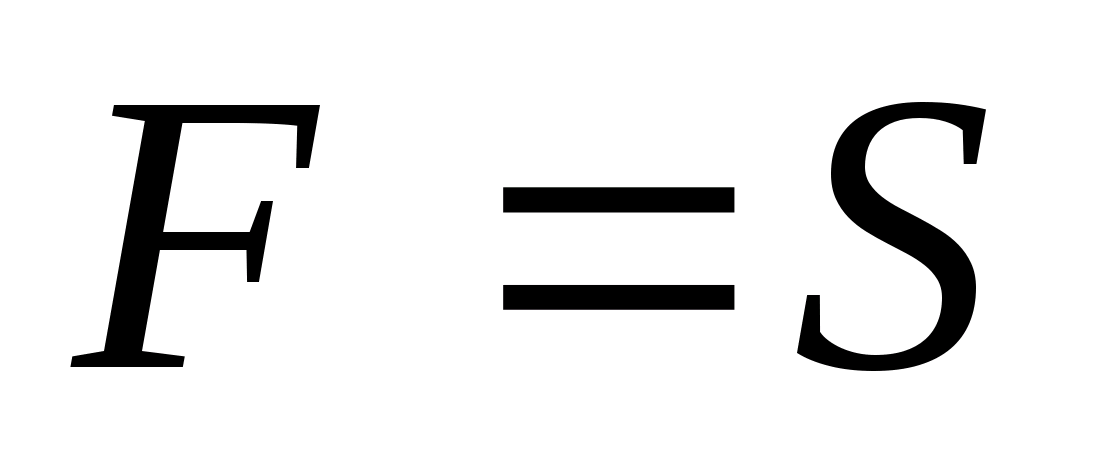 ,
откуда следует, что
,
откуда следует, что
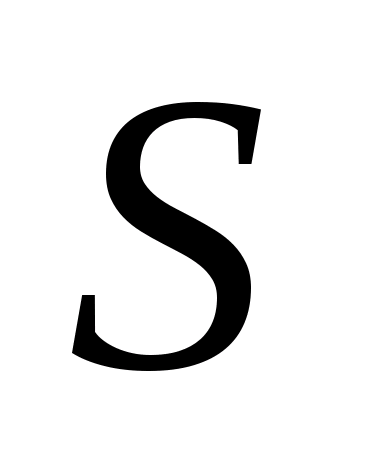 связно.
связно.
1.3 Топологические преобразования топологических пространств
1.3.1 Непрерывные отображения
Пусть даны топологические пространства (Х, Ф), (У, W) и отображение
 :
X
У.
:
X
У.
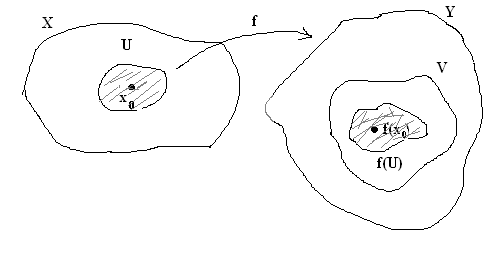
Определение
1.
Отображение
 :
X
У называется непрерывным в точке х>0
>
Х, если для каждой окрестности V
точки f(x>0>)
существует такая окрестность U
точки х>0>,
что
:
X
У называется непрерывным в точке х>0
>
Х, если для каждой окрестности V
точки f(x>0>)
существует такая окрестность U
точки х>0>,
что
 (U)
V.
(U)
V.
Определение
2.
Отображение
 :
X
У называется непрерывным на множестве
Н
Х, если
:
X
У называется непрерывным на множестве
Н
Х, если
 непрерывно в каждой его точке.
непрерывно в каждой его точке.
Если
Н = Х, то говорят, что
 непрерывно на Х.
непрерывно на Х.
Определение
3.
Если
 :
X
У, В
У, то множество всех точек х>0
>
Х, для каждой из которых имеем
:
X
У, В
У, то множество всех точек х>0
>
Х, для каждой из которых имеем
 (x>0>)
В называется прообразом множества В, и
обозначается
(x>0>)
В называется прообразом множества В, и
обозначается
 -1(B),
причем имеет место
-1(B),
причем имеет место
 (
( -1(B))
B.
-1(B))
B.
Теорема
1.
Для того, чтобы отображение
 :
X
У было непрерывным на Х, необходимо и
достаточно, чтобы прообраз любого
открытого (замкнутого) множества был
открытым (замкнутым) множеством.
:
X
У было непрерывным на Х, необходимо и
достаточно, чтобы прообраз любого
открытого (замкнутого) множества был
открытым (замкнутым) множеством.
Доказательство. 1. Необходимость.
Пусть
 :
Х
У непрерывно, V
открытое множество в У, а
:
Х
У непрерывно, V
открытое множество в У, а
U
=
 -1(V).
-1(V).
Докажем,
что U
– открытое множество в Х. Пусть
 – любая точка из U
и b
=
– любая точка из U
и b
=
 (
( ).
Множество V
является окрестностью точки b.
Так как
).
Множество V
является окрестностью точки b.
Так как
 – непрерывно, то найдётся окрестностью
U
– непрерывно, то найдётся окрестностью
U точки
точки
 ,
что
,
что
 (U
(U )
V.
)
V.
Очевидно,
U
 -1(V)
= U.
-1(V)
= U.
Так
как U
=
 U
U ,
то U
– открытое множество.
,
то U
– открытое множество.
Достаточность.
Возьмём любую точку

Х и пусть b
=
Х и пусть b
=
 (
( ).
Если V
– произвольная окрестность точки b,
то U
=
).
Если V
– произвольная окрестность точки b,
то U
=
 -1(V)
открытое множество и является окрестностью
точки
-1(V)
открытое множество и является окрестностью
точки
 .
Поскольку
.
Поскольку
 (U)
V,
то
(U)
V,
то
 – непрерывно в точке
– непрерывно в точке
 ,
что требовалось доказать.
,
что требовалось доказать.
Для замкнутых множеств теорема доказывается переходом к дополнительным множествам.
Замечание. При непрерывном отображении образ замкнутого
(открытого) множества может быть не замкнутым (не открытым) множеством.
Теорема 2. Пусть X, Y, Z – топологические пространства.
Если
отображения f
 и g
и g
 непрерывны,
то непрерывна и их композиция:
непрерывны,
то непрерывна и их композиция:
g f: Х Z.
Доказательство. Пусть W открытое множество пространства Z. Так как g – непрерывно, то по предыдущей теореме
G -1(W) = V – открыто в У.
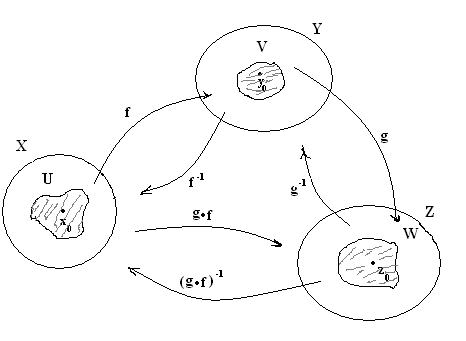
Тогда аналогично, U = f-1(V) – открыто в Х.
Но U = f -1 (g -1(W)) = (gf) -1(W) – прообраз W.
Теорема доказана.
Пример непрерывного отображения
Рассмотрим
плоскость П и прямую ℓ
П с естественными топологиями. Докажем,
что ортогональное проектирование
 :
П
ℓ является непрерывным отображением.
:
П
ℓ является непрерывным отображением.
Действительно, пусть для произвольной точки А П
 (А)
= А>0.>
(А)
= А>0.>
Пусть
V– -окрестность
точки А>0>,
то есть V
– интервал.
-окрестность
точки А>0>,
то есть V
– интервал.
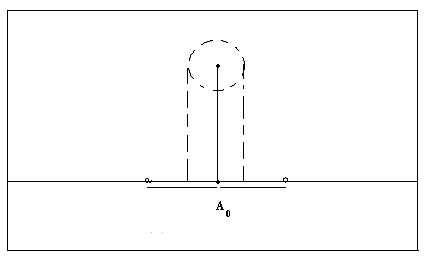
В
точке А рассмотрим открытый круг радиуса
=
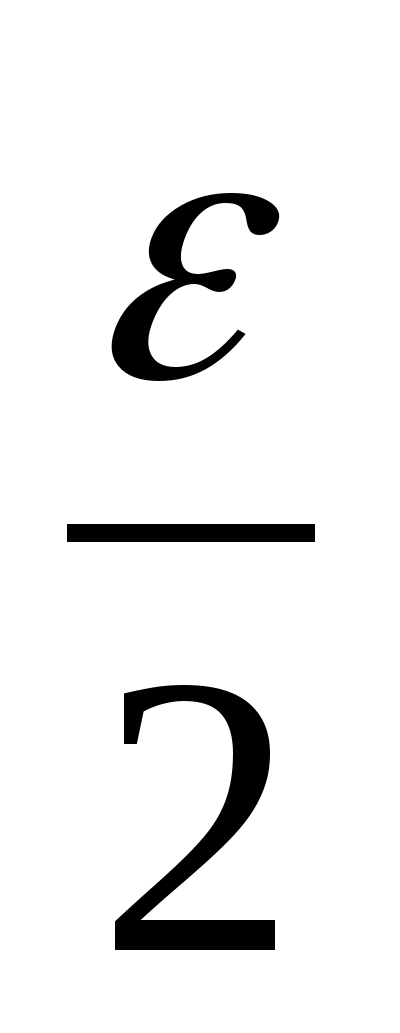 ,
то есть окрестность U
точки А. Очевидно,
,
то есть окрестность U
точки А. Очевидно,
 (U)
V
и, следовательно,
(U)
V
и, следовательно,
 –
является
непрерывным отображением в точке А.
–
является
непрерывным отображением в точке А.
Так
как А – произвольная точка плоскости
П, то
 – непрерывное отображение.
– непрерывное отображение.
1.3.2 Топологические отображения
Определение
1.
Пусть даны топологические пространства
Х и У. Отображение
 :
Х
У называется топологическим
(гомеоморфизмом), если
:
Х
У называется топологическим
(гомеоморфизмом), если
 – биекция и, при этом, отображения
– биекция и, при этом, отображения
 и
и
 -1
– непрерывные.
-1
– непрерывные.
Свойство 1. Всякое тождественное отображение е: Х Х является гомеоморфизмом.
Доказательство непосредственно вытекает из определения.
Свойство 2. Если X, У, Z – топологические пространства, а отображения
 :
Х
У,
:
Х
У,
g: У Z
являются
топологическими, то и их композиция g
 :
Х
Z
– также топологическое отображение.
:
Х
Z
– также топологическое отображение.
Действительно,
композиция биекций является биекцией.
Произведение непрерывных отображений
является непрерывным отображением.
Обратным к g
 :
ХZ
отображением является отображение
:
ХZ
отображением является отображение
(g
 )
-1
=
)
-1
=
 -1
g
-1.
-1
g
-1.
Так как отображения
 :
Х
У,
:
Х
У,
g: У Z
являются топологическими, то обратные к ним отображения
 -1:
У
Х,
-1:
У
Х,
g -1: Z У
являются непрерывными.
Поэтому
и их композиция
 -1
g
-1
–
непрерывное отображение, а следовательно,
и отображение (g
-1
g
-1
–
непрерывное отображение, а следовательно,
и отображение (g
 )-1
непрерывное.
)-1
непрерывное.
Свойство доказано.
Свойство
3.
Если
 :
Х
У – гомеоморфизм, то и
:
Х
У – гомеоморфизм, то и
 -1:
У
Х – гомеоморфизм.
-1:
У
Х – гомеоморфизм.
Доказательство.
Действительно, так как
 :
Х
У – гомеоморфизм, то
:
Х
У – гомеоморфизм, то
 – биекция. Поэтому обратное к нему
отображение
– биекция. Поэтому обратное к нему
отображение
 -1
также биекция. При этом, согласно условию
-1
также биекция. При этом, согласно условию
 -1
–
непрерывно. Учитывая, что
-1
–
непрерывно. Учитывая, что
( -1)
-1
=
-1)
-1
=
 ,
,
имеем:
отображение
 --1
–
гомеоморфизм.
--1
–
гомеоморфизм.
Свойство доказано.
Определение
2.
Говорят, что топологическое пространство
Х гомеоморфно топологическому пространству
У, если существует гомеоморфизм
 :
Х
У.
:
Х
У.
Учитывая выполнимость перечисленных выше свойств гомеоморфизма, получим, что отношение гомеоморфности топологических пространств является отношением эквивалентности.
Про гомеоморфные пространства также говорят, что они топологически эквивалентны. Обозначаем:
Х
 У.
У.
Кроме того, мы одновременно показали, что (с учётом ассоциативности произведения топологических отображений) множество всех гомеоморфизмов пространства на себя по умножению есть группа.
В связи с этим свойства фигур, сохраняющиеся при гомеоморфизмах, называются топологическими, а топология изучает свойства фигур, инвариантные относительно гомеоморфных отображений топологических пространств.
Таким образом, топология изучает геометрию группы всех гомеоморфизмов пространства на себя.
1.3.3 Примеры гомеоморфных пространств и гомеоморфизмов
Пример
1.
Задана числовая прямая с естественной
топологией. Доказать, что любые два
интервала ( ,
b)
и (c,
d)
гомеоморфные.
,
b)
и (c,
d)
гомеоморфные.
Действительно, гомеоморфизм между ними устанавливается, например, линейной функцией
у
=
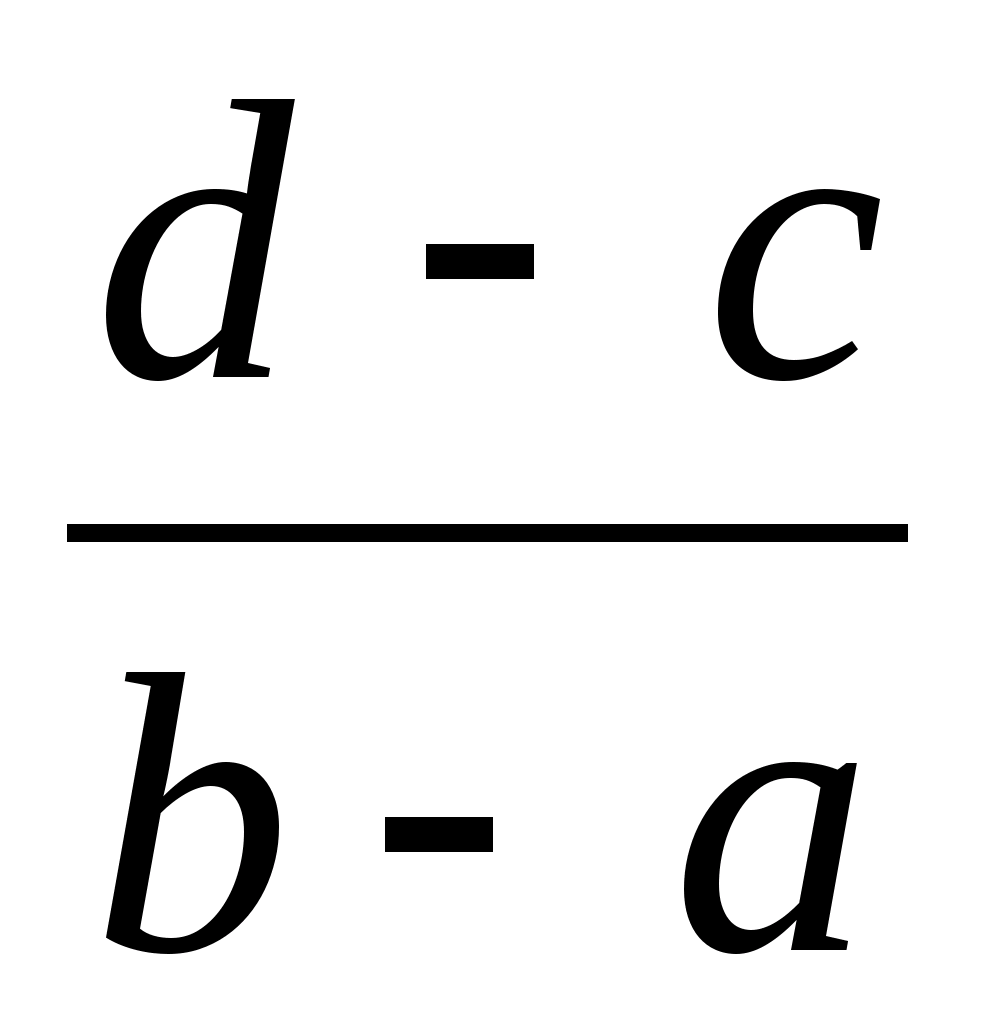 (х –
(х –
 )
+ с,
)
+ с,
где
х
( ,
b),
а у
(с, d).
,
b),
а у
(с, d).
Пример 2. Задано трехмерное евклидово пространство с топологией, порожденной метрикой. Доказать, что сфера гомеоморфна поверхности куба.
Для того, чтобы установить гомеоморфизм между ними, достаточно поместить их центры в одну точку и произвести из неё центральное проектирование.

Пример 3. Задана числовая прямая с естественной топологией. Доказать, что интервал и прямая гомеоморфные. Гомеоморфизм между ними можно установить следующей функцией:
у
= tg
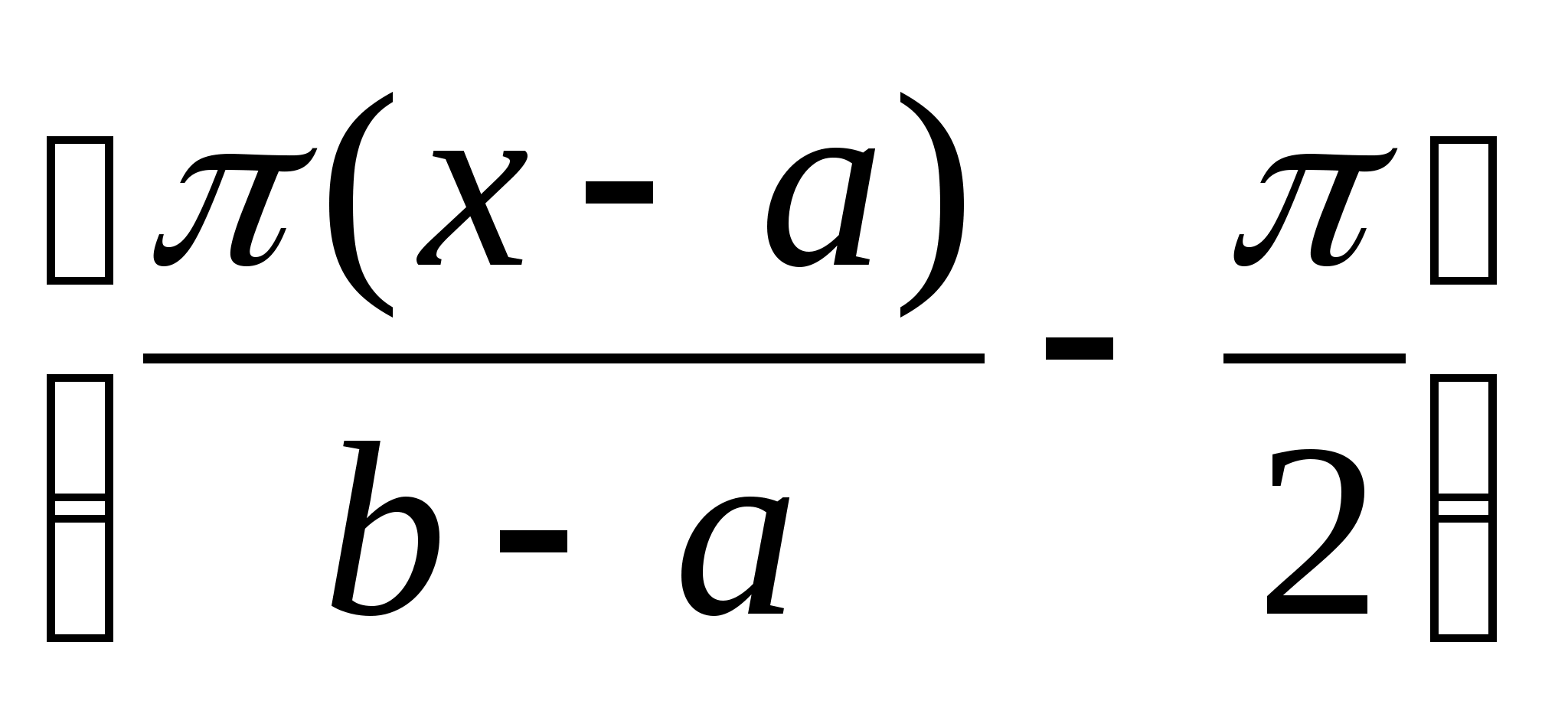
х Х = (а, b),
у У = R.
Теорема.
Пусть
 :
Х
У – непрерывное взаимно – однозначное
отображение и
:
Х
У – непрерывное взаимно – однозначное
отображение и
 (Х)
= У. Тогда, если Х – компактно, а У –
хаусдорфово пространство, то
(Х)
= У. Тогда, если Х – компактно, а У –
хаусдорфово пространство, то
 – гомеоморфизм.
– гомеоморфизм.
2. Топологические свойства поверхностей
2.1 Понятие двумерного многообразия
2.1.1 Определение двумерного многообразия
Важнейшим для геометрии классом топологических пространств являются двумерные многообразия.
Определение 1. Двумерным многообразием называется хаусдорфово топологическое пространство со счетной базой, каждая точка которого имеет окрестность, гомеоморфную открытому кругу.
Локально у двумерных многообразий те же топологические свойства, что и у евклидовой плоскости.
В топологии под термином «поверхность» понимают именно двумерное многообразие. Поэтому в дальнейшее мы не будем различать эти два понятия.
Примерами поверхностей являются любая область на евклидовой плоскости, сфера, эллипсоид, гиперболоиды, параболоиды в евклидовом пространстве с естественной топологией.
В дальнейшем мы часто будем встречать поверхность, которую называют тором. Поэтому определим ее следующим образом.
Определение 2. Тором в пространстве Е3 называется множество точек, образованное вращением окружности вокруг оси, лежащей в плоскости окружности и не пересекающейся с этой окружностью.
Компактные поверхности называют замкнутыми поверхностями. Например, сфера, тор – замкнутые поверхности, а параболоиды и гиперболоиды не являются замкнутыми поверхностями.
Определение 3. Двумерным многообразием с краем или поверхностью с краем называется хаусдорфово топологическое пространство со счетной базой, каждая точка которого имеет окрестность, гомеоморфную открытому кругу или полукругу вместе с диаметром.
Те точки поверхности с краем, у которых есть окрестность гомеоморфная открытому кругу, называются внутренними точками поверхности, а те ее точки, которые имеют окрестности, гомеоморфные полукругу вместе с диаметром, называются краевыми точками.
В дальнейшем будем считать, что для данной поверхности внутренняя ее точка одновременно не может быть ее краевой точкой.
Множество внутренних точек любой поверхности F с краем открыто в F и само является поверхностью. Поэтому множество точек края в F замкнуто и его обозначают F. Отметим, что F является границей в F множества внутренних точек. Каждая поверхность является частным случаем поверхности с краем, край которой пуст.
Если край F поверхности с краем F не пуст, то он имеет простое строение: каждая его компонента гомеоморфна либо окружности, либо прямой. В частности, когда F компактна, то ее край состоит из конечного числа компонент, каждая из которых гомеоморфна окружности. Так, край кольца – это две окружности, край боковой поверхности цилиндра – также две окружности.

В дальнейшем мы будем часто сталкиваться с процессом построения новых поверхностей, который называют операцией склеивания. Эта операция заключается в следующем. Берутся две поверхности с краем F и F, и на их краях F и F выделяются некоторые гомеоморфные между собой части и .
Соответствующие при данном гомеоморфизме точки Х и
X отождествляются, т.е. считаются за одну точку Х. Одновременно склеиваются и их окрестности. При этом получается новая поверхность с краем, склеенная из поверхностей F и F.
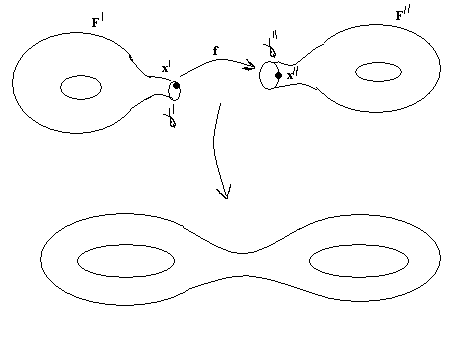
Например, многогранную поверхность можно считать склеенной из ее граней, а поверхность цилиндра вращения – склеенной из ее боковой поверхности и двух оснований. Склеивать можно и отдельные части края одной и той же поверхности с краем. Например, таким склеиванием получается поверхность, которую называют листом Мебиуса.
2.1.2 Примеры поверхностей, полученных склеиванием
Пример 1. Лист Мебиуса, как пример поверхности с краем был описан в 1862 1865 годах в работах немецких математиков Мебиуса и Листинга. Поверхность получается следующим образом. Лента прямоугольной формы один раз перекручивается, и затем ее концы склеиваются.
Полученная поверхность с краем имеет лишь одну сторону. Например, перемещая кисточку по ленте Мебиуса, мы придем к тому же месту, с которого начинали закрашивание, но с обратной стороны. Перемещая кисточку дальше, мы закрасим всю ленту Мебиуса и убедимся, что у нее нет «второй стороны».
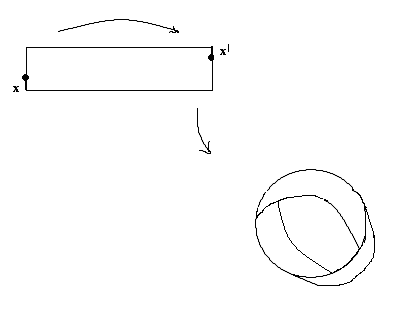
Край листа Мебиуса гомеоморфен окружности, поэтому Лист Мебиуса не гомеоморфен кольцу, у которого край состоит из двух окружностей.
Пример 2. Если на торе вырезать круглую дыру, то мы получим поверхность с краем, которая называется ручкой. Край полученной поверхности состоит из одной кривой, гомеоморфной окружности.

Пример 3. Рассмотрим сферу, в которой вырезано p круглых дыр, и заклеим каждую из дыр ручкой.
Полученная поверхность называется сферой с p ручками. Сфера с одной ручкой гомеоморфна тору, а сфера с двумя ручками поверхности «кренделя» (получающейся склеиванием двух ручек).

2.2 Эйлерова характеристика поверхности
2.2.1 Правильные многогранники. Теорема Эйлера
Рассмотрим известные в евклидовой геометрии правильные многогранники. В следующей таблице указано название, число вершин, ребер и граней этих пяти правильных многогранников.
|
Название многогранников |
Число вершин |
Число ребер |
Число граней |
|
Тетраэдр |
4 |
6 |
4 |
|
Куб |
8 |
12 |
6 |
|
Октаэдр |
6 |
12 |
8 |
|
Додекаэдр |
20 |
30 |
12 |
|
Икосаэдр |
12 |
30 |
20 |
Из рассмотрения этой таблицы видно, что для каждого правильного многогранника имеет место соотношение:
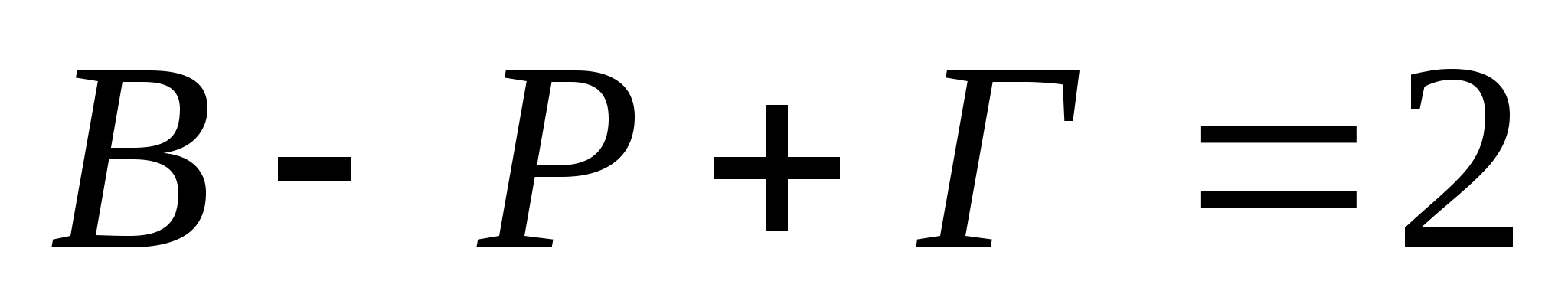 , (1)
, (1)
где В число вершин многогранника, Г число граней, Р число ребер. Соотношение (1) легко проверить также для пирамид, призм и других многогранников. Эйлер впервые подметил и доказал это замечательное свойство многогранников.
Уточним формулировку теоремы Эйлера. Прежде всего заметим, что любая грань каждого из рассмотренных многогранников гомеоморфна кругу. Далее, поверхность каждого из рассмотренных многогранников (или, вообще, любого выпуклого многогранника) гомеоморфна сфере: если О произвольная внутренняя точка многогранника, а S сфера с центром О, содержащая внутри себя этом многогранник, то проекция поверхности на сферу S из центра О представляет собой искомый гомеоморфизм.
Теорема Эйлера. Для всякого многогранника, поверхность которого гомеоморфна сфере, а каждая грань гомеоморфна кругу справедливо соотношение (1).
Можно придать этой теореме чисто топологическую формулировку. Для этого заметим, что все вершины и ребра многогранника образуют связный граф, который разбивает поверхность многогранника на отдельные грани (т.е. куски, гомеоморфные кругу). Мы получаем следующее (более общее, чем теорема Эйлера) утверждение:
Пусть на сфере (или гомеоморфной ей поверхности) начерчен связанный граф G, имеющий В вершин и Р ребер и разбивающий сферу на Г областей (граней), тогда справедливо соотношение:
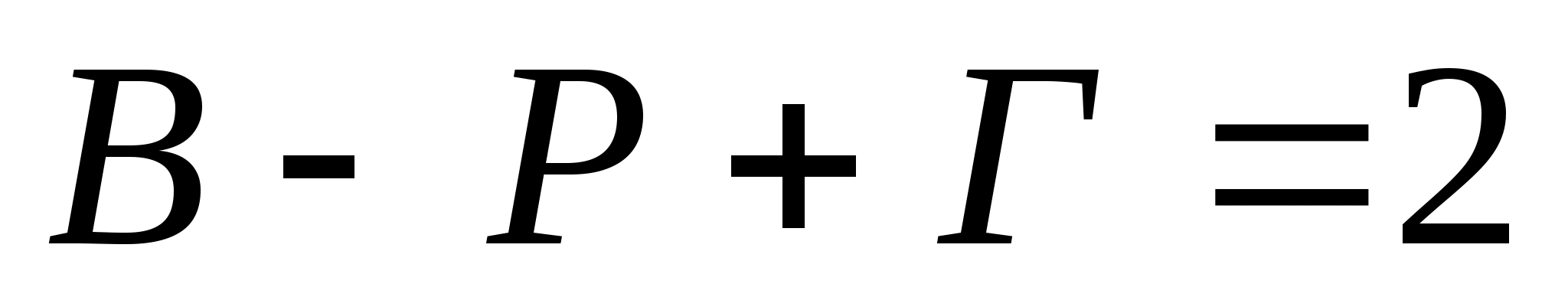 . (2)
. (2)
В дальнейшем простой дугой будем называть гомеоморфный образ отрезка, а простой замкнутой кривой или циклом – гомеоморфный образ окружности.
2.2.2 Понятие сети
Определение 1. Пусть Q – компактная поверхность с краем. Сетью на Q назовем любой набор конечного числа точек А>1>, А>2>, …, А>m> и конечного числа простых дуг >1>, >2>,,>n>, которые имеют концы в точках А>1>, А>2>, …, А>m> и не пересекаются друг с другом во внутренних точках.
Точки А>1>, А>2>, …, А>m> называются вершинами сети, дуги >1>, >2>,,>n>> >– ребрами сети. Областями сети назовем компоненты множества
Q
\ ((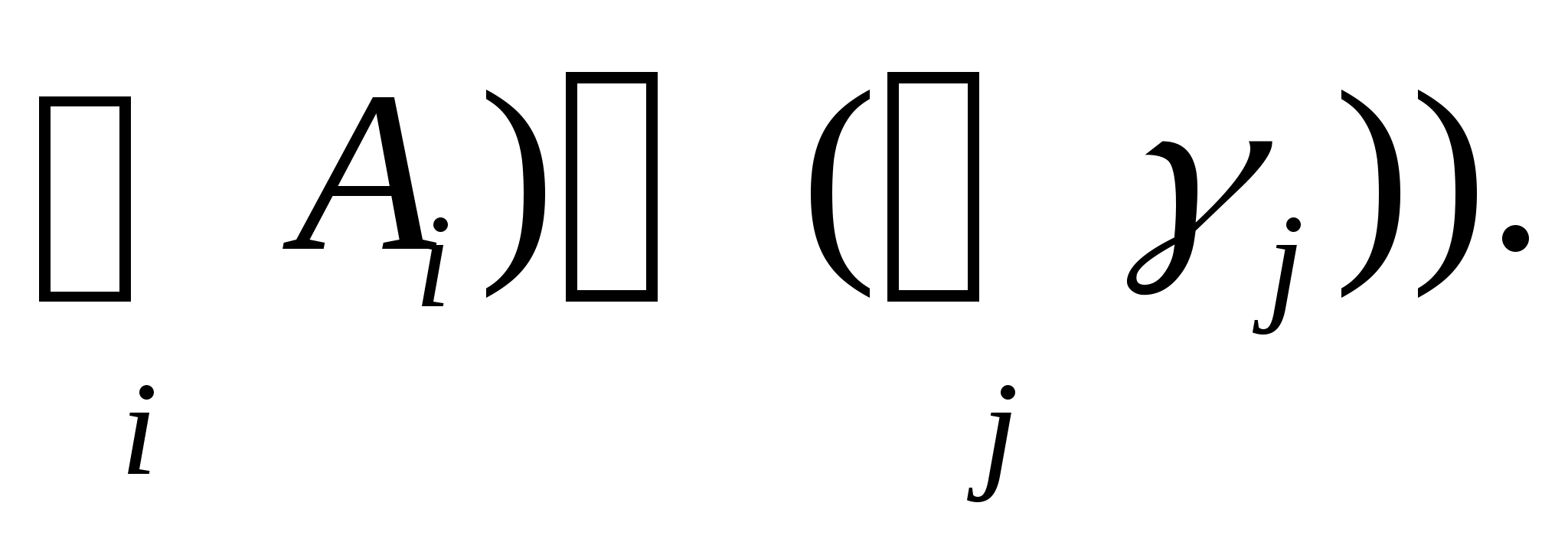
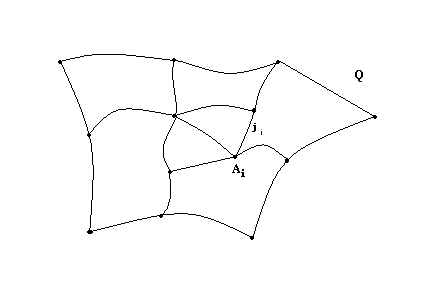
Определение 2. Если каждая область сети гомеоморфна открытому кругу, то говорят, что сеть задает клеточное разбиение поверхности с краем Q. В этом случае вершины сети называем вершинами клеточного разбиения, ребра сети – ребрами клеточного разбиения, а области сети – областями клеточного разбиения.
Пусть Q поверхность (с краем или без края, двусторонняя или односторонняя), которая допускает разбиение на многоугольники. Это означает, что на поверхности можно задать клеточное разбиение, разбивающее ее на конечное число областей, гомеоморфных кругу. Обозначим число вершин и ребер сети через В и Р, а число многоугольников, на которые Q разбивается этой сетью через Г. Число
(Q) = В Р + Г (3)
называется эйлеровой характеристикой поверхности Q.
Строго говоря, число (2) определяется не самой поверхностью Q, а выбором ее разбиения на многоугольники. Однако теорема Эйлера показывает, что для поверхности Q, гомеоморфной сфере, эйлерова характеристика не зависит от выбора разбиения на многоугольники:
(Q) = 2.
Теорема 1. Для любой поверхности Q ее эйлерова характеристика (Q) не зависит от выбора разбиения на многоугольники, а определяется самой поверхностью, т.е. является ее топологическим инвариантом.
Теорема 2. Эйлерова характеристика поверхности является ее топологическим инвариантом, т.е., если поверхности Q>1> и Q>2> гомеоморфны, то (Q>1>) = (Q>2>).
Доказательство. В самом деле, при гомеоморфизме
f: Q>1>Q>2>
сеть G>1>, заданная на поверхности Q>1>, переходит в сеть G>2 >= f(G>1>) на поверхности Q>2>, причем число вершин, ребер и граней на поверхности Q>2> будет столько же, сколько и на поверхности Q>1>.
Определение 3. Будем говорить, что двумерное многообразие Ẽ получено из Е и Е’ склеиванием по совокупности гомеоморфизмов
f>i>: >I>> > >I>, i=1,2,…, k, если мы имеем склеивание по каждому гомеоморфизму f>i>: >I>> > >I> отдельно и при этом компоненты края все попарно различны.
Теорема 3. Если двумерное многообразие Ẽ получено из Е и Е склеиванием по совокупности гомеоморфизмов f>i>: >I>> > >I>, i=1,2,…, k, то эйлерова характеристика многообразия Ẽ равна сумме эйлеровых характеристик многообразий Е и Е.
Доказательство.
Пусть Е
Е,
К и К
их клеточные разбиения. Очевидно, всегда
можно выбрать клеточные разбиения
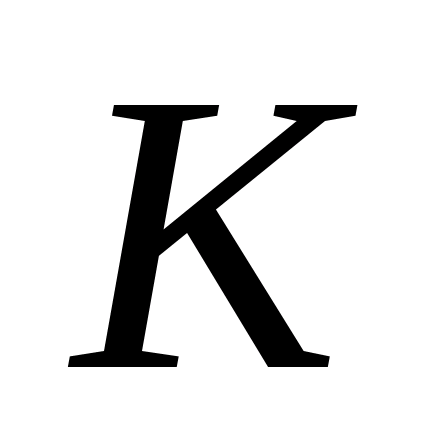 и К
такими, что гомеоморфизм f>i>:
>I>>
>>I>
отображает вершину из К на вершину из
К
и, наоборот. Обозначим >0>,
>1>,
>2>,
(>0>,
>1>,
>2>)
– число вершин, сторон и клеток в К (К),
р>0
>(р>0>)
– число вершин расположенных на
отождествляемых компонентах края. При
этом р>0
>=
р>0>.
Объединяя все клетки К и К
мы получим новое клеточное разбиение
и К
такими, что гомеоморфизм f>i>:
>I>>
>>I>
отображает вершину из К на вершину из
К
и, наоборот. Обозначим >0>,
>1>,
>2>,
(>0>,
>1>,
>2>)
– число вершин, сторон и клеток в К (К),
р>0
>(р>0>)
– число вершин расположенных на
отождествляемых компонентах края. При
этом р>0
>=
р>0>.
Объединяя все клетки К и К
мы получим новое клеточное разбиение
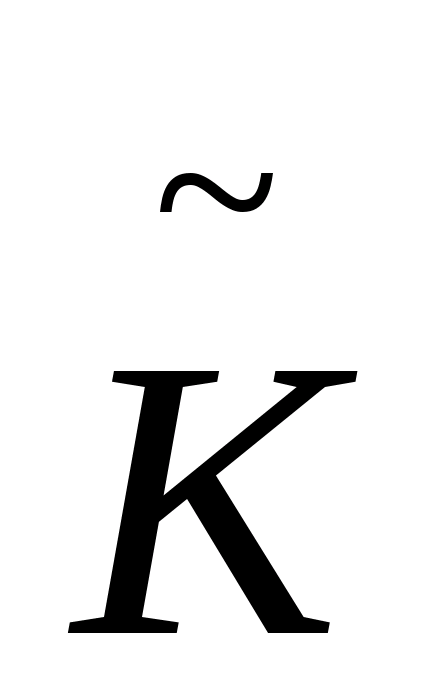 для многообразия Ẽ. При этом
для многообразия Ẽ. При этом
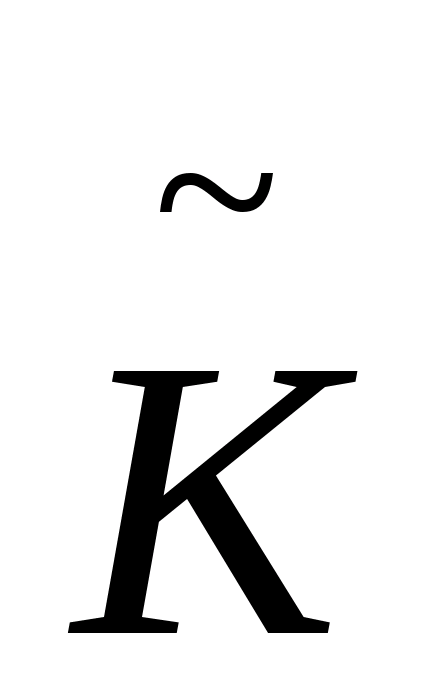 имеет: вершин
имеет: вершин
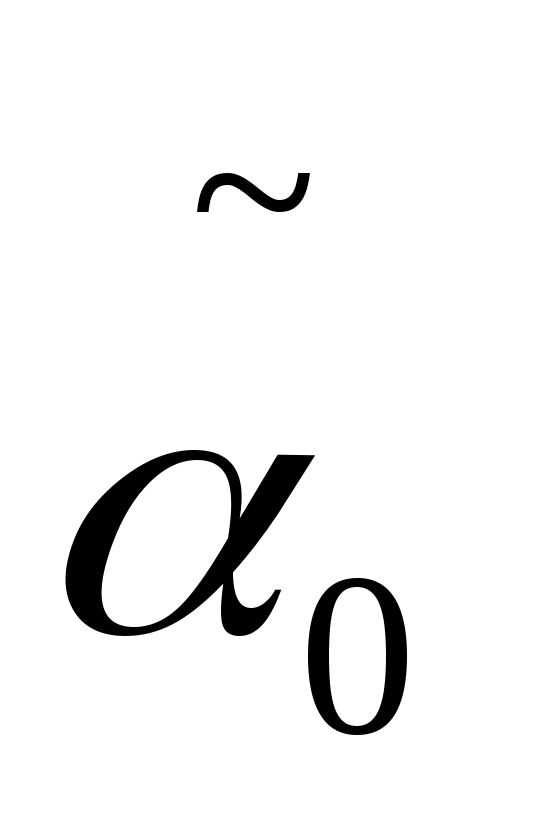 =
>0
>+
>0>
– р>0>,
сторон
=
>0
>+
>0>
– р>0>,
сторон
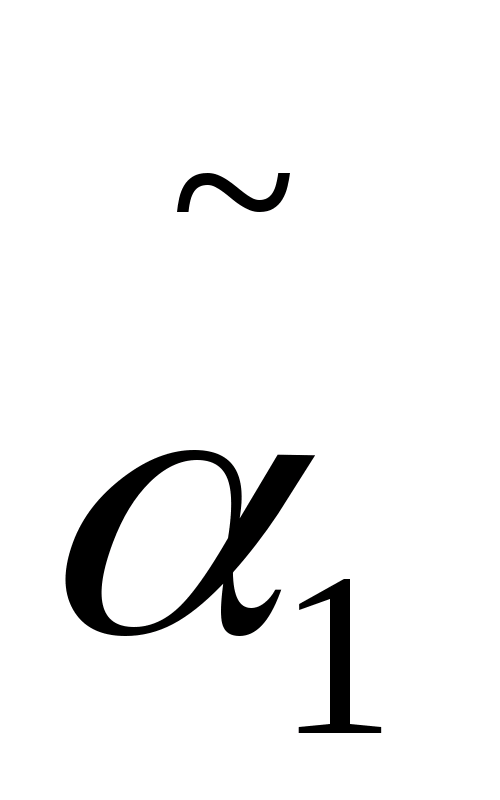 =
>1>+
>1>
– р>0,>
клеток
=
>1>+
>1>
– р>0,>
клеток
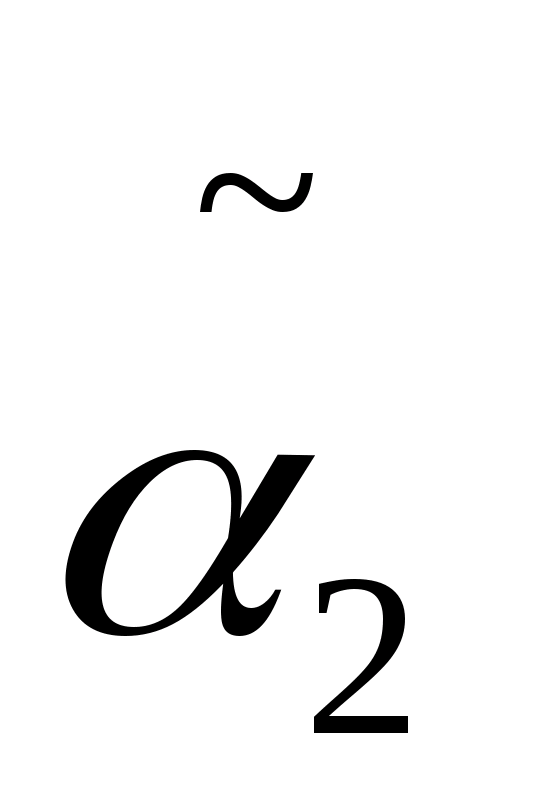 =
>2
>+
>2>.
=
>2
>+
>2>.
Следовательно,
(Ẽ)
=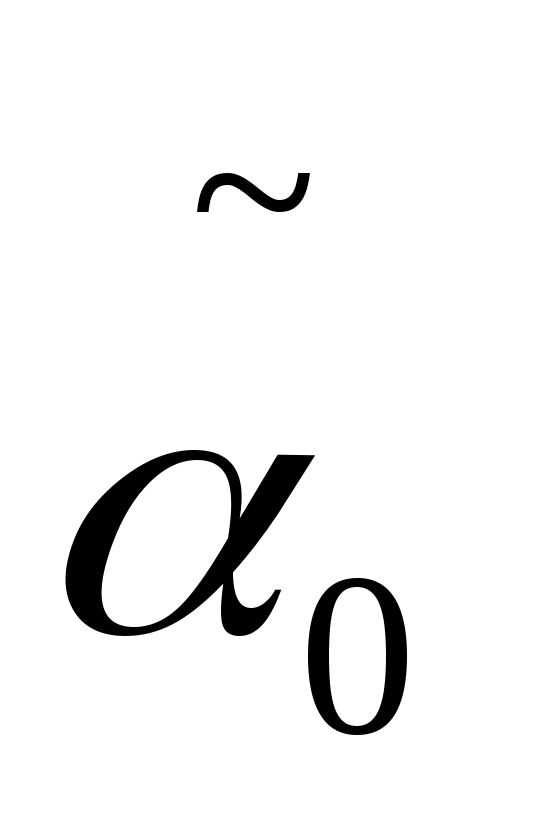 –
–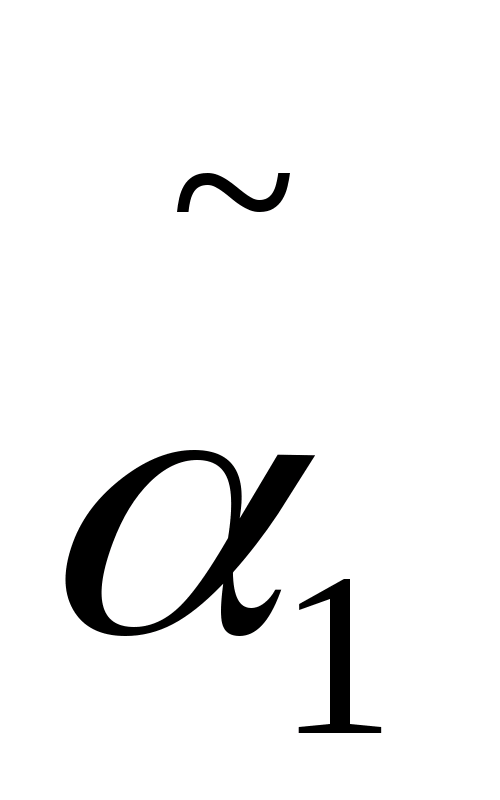 +
+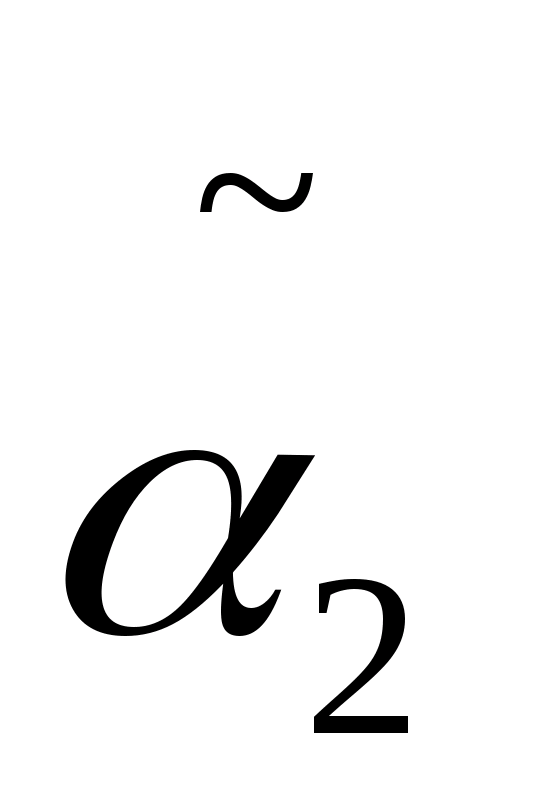 =(>0
>+
>0>
– р>0>)
– (>1>+
>1>
– р>0>)
+ (>2
>+
>2>)
=
(Е) +
(Е’).
=(>0
>+
>0>
– р>0>)
– (>1>+
>1>
– р>0>)
+ (>2
>+
>2>)
=
(Е) +
(Е’).
Теорема доказана.
Определение 4. Многогранник нулевого рода называется топологически правильным, если все его грани имеют одно и то же число вершин, а к каждой вершине подходит одно и то же число ребер.
Найдем все топологически правильные многогранники. Пусть Р один из них, n – число вершин каждой из его грани, m – число ребер, подходящих к каждой вершине. Так как каждое ребро является общей стороной двух его граней, то
n>2> = 2 >1. >(4)
Так как каждое ребро подходит к двум вершинам, то
m>0> = 2 >1. >(5)
Из (1) и (2) получим:
>2>
=
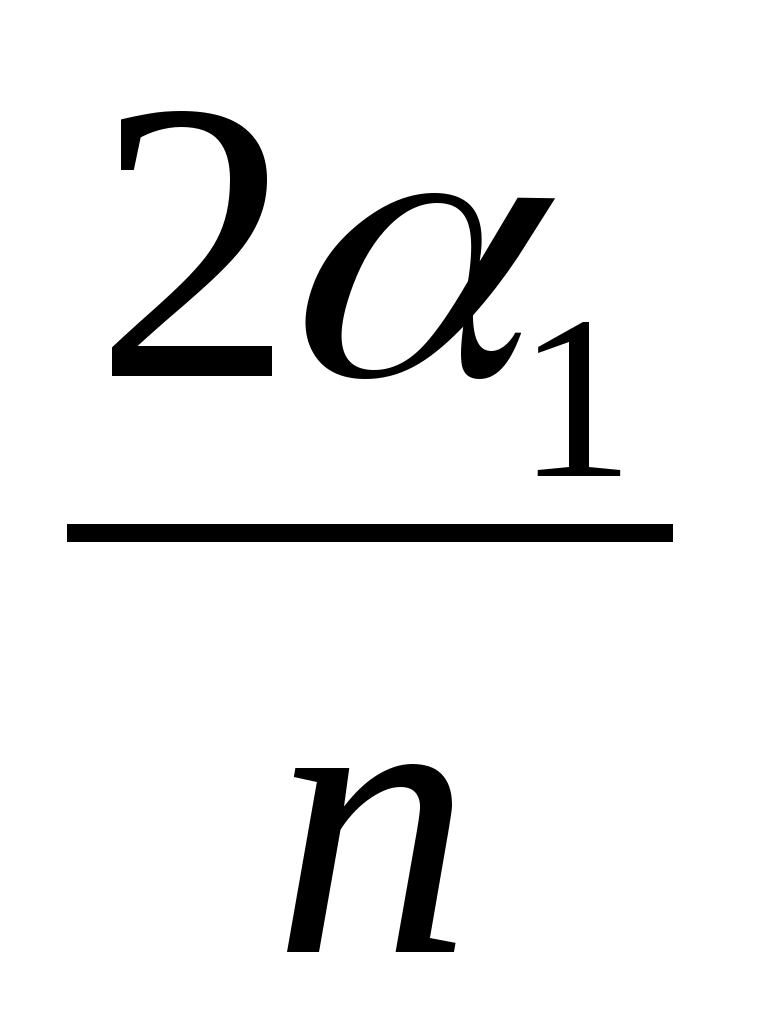 ,
>0>
=
,
>0>
=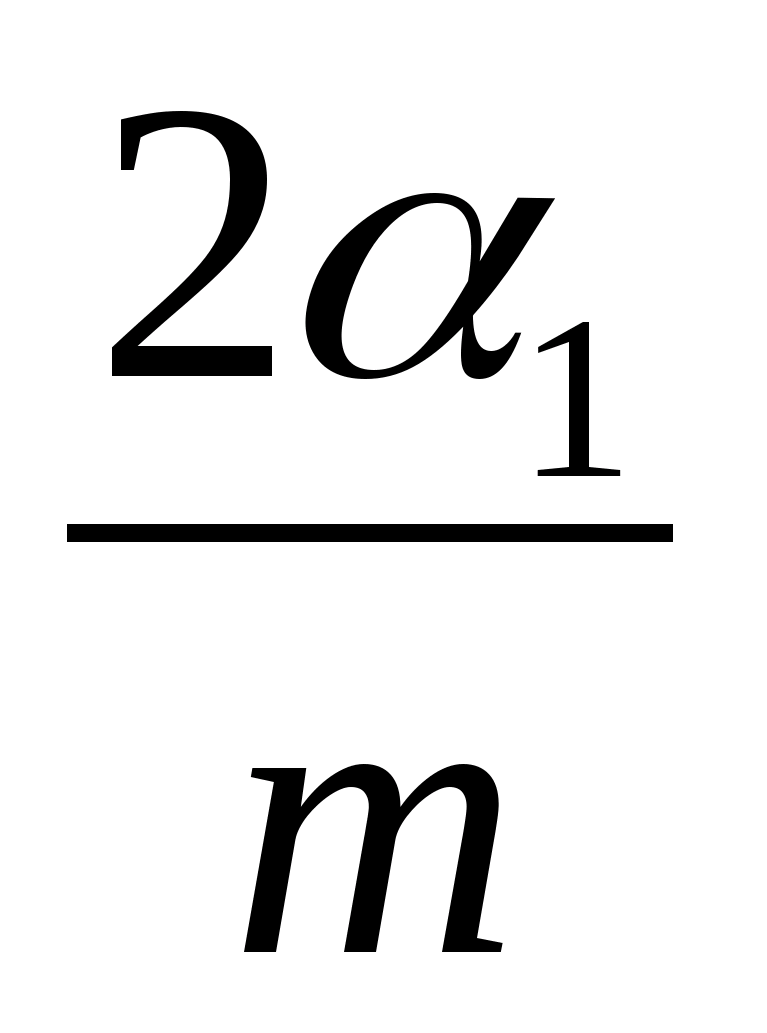 .
.
Подставляя эти равенства в формулу Эйлера, получим
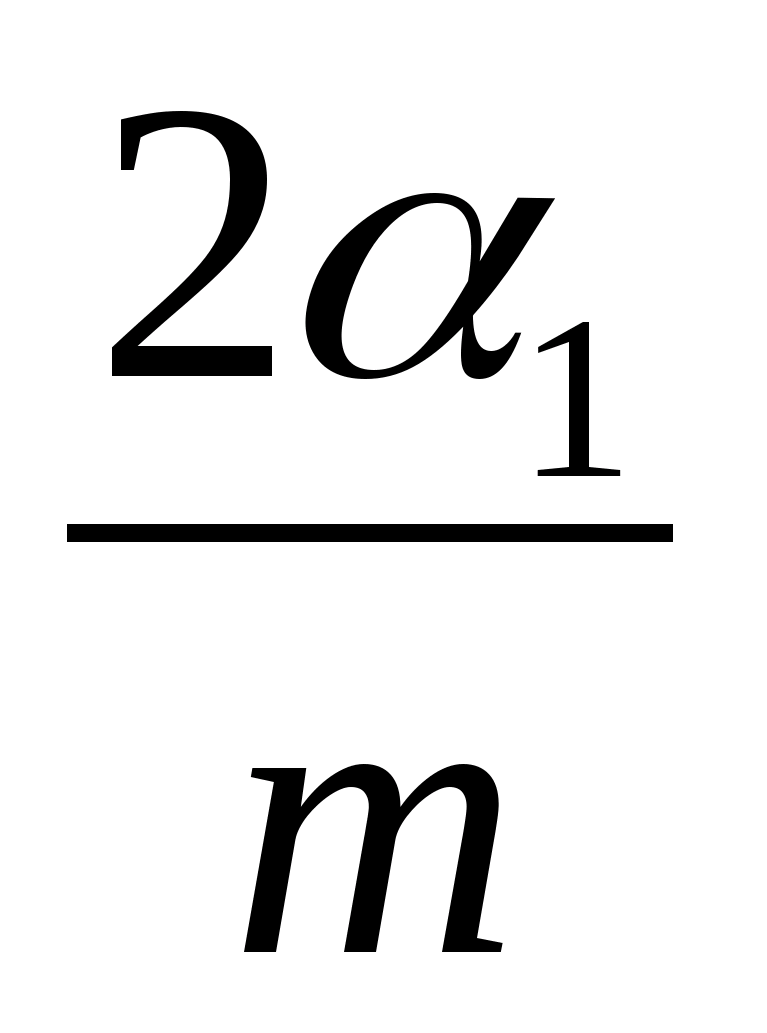 – >1
>+
– >1
>+
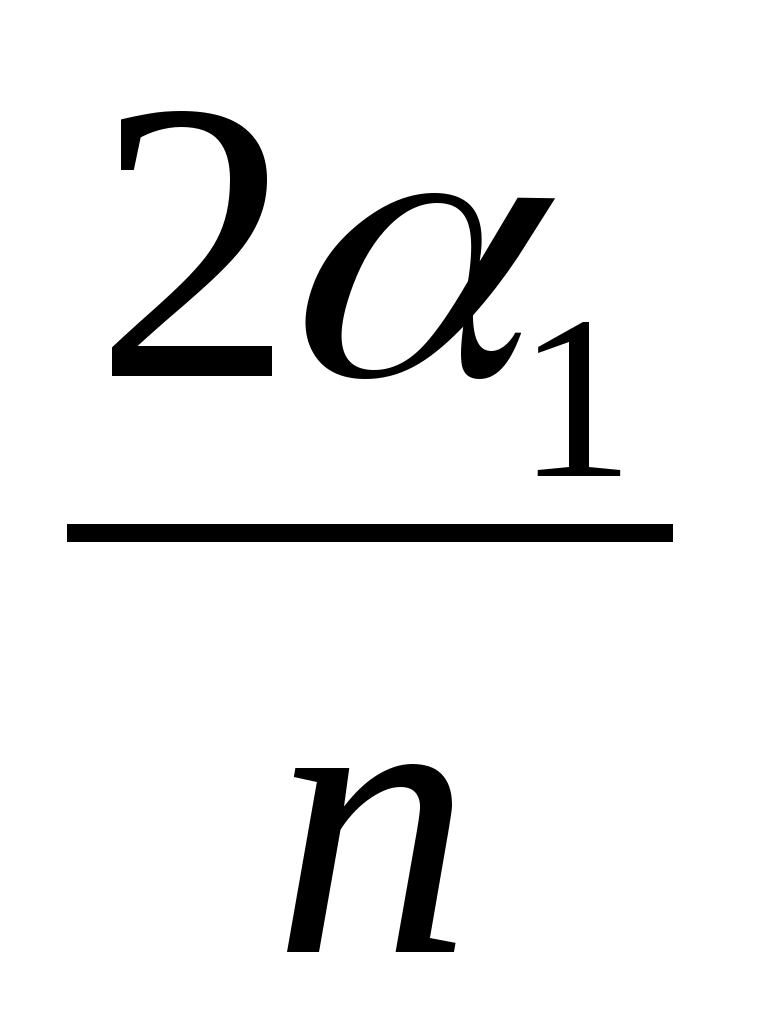 = 2.
= 2.
Преобразовав это равенство, получим
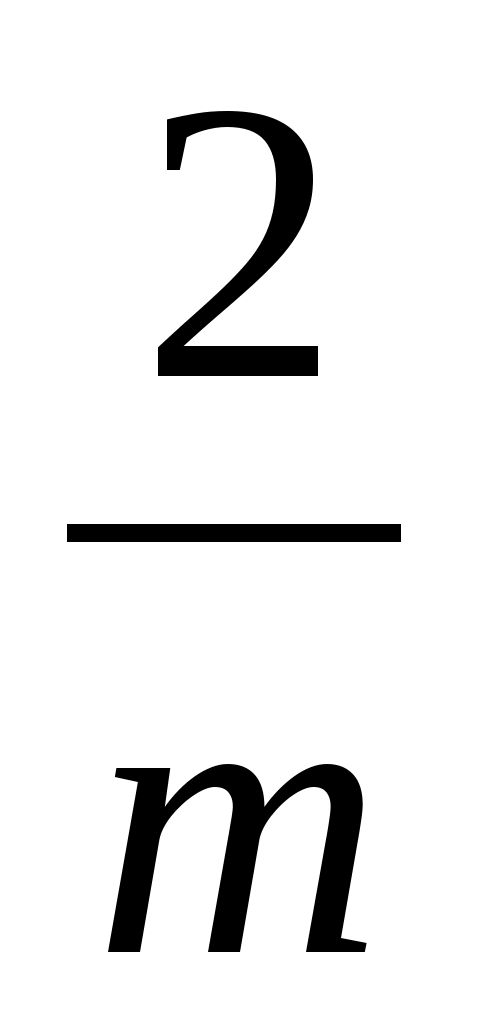 +
+
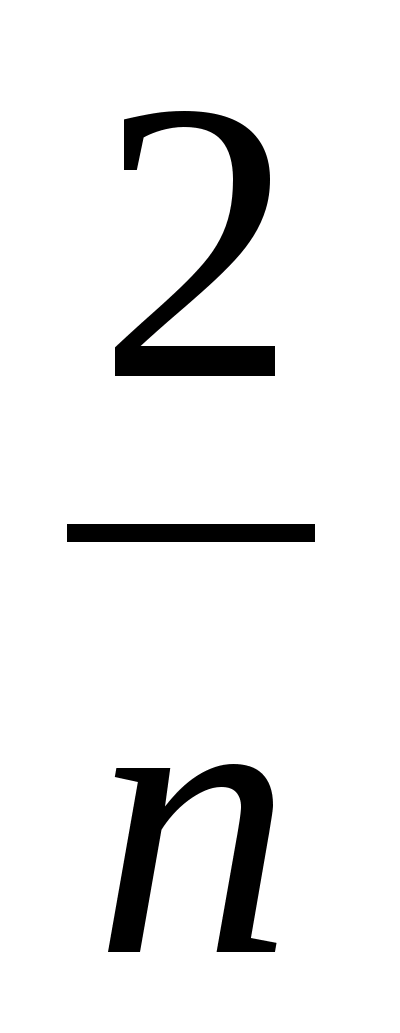 =
=
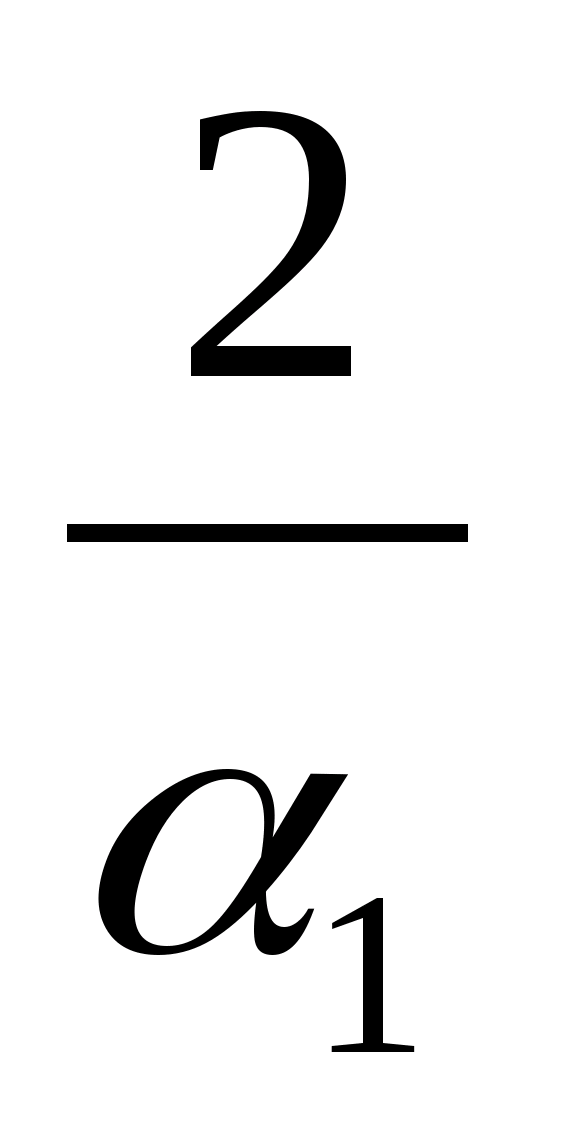 + 1,
+ 1,
что приводит нас к неравенству
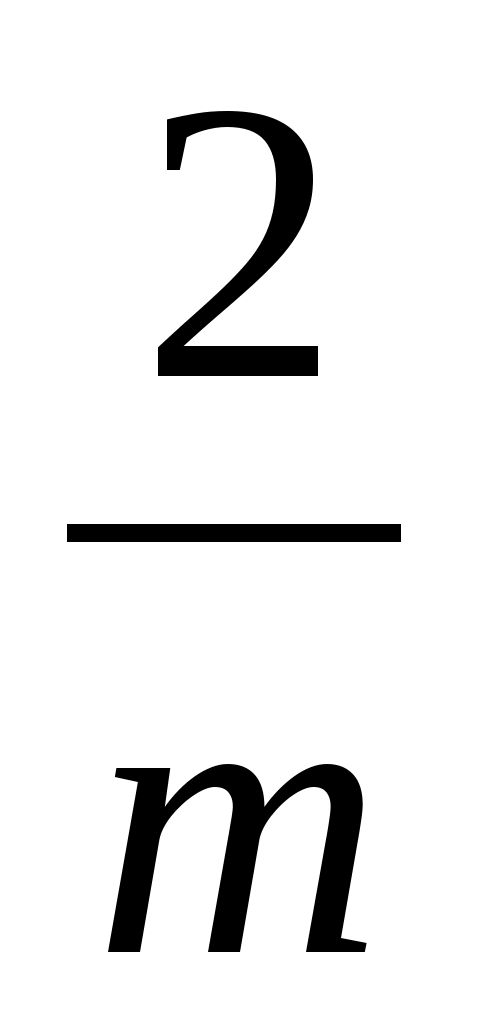 +
+
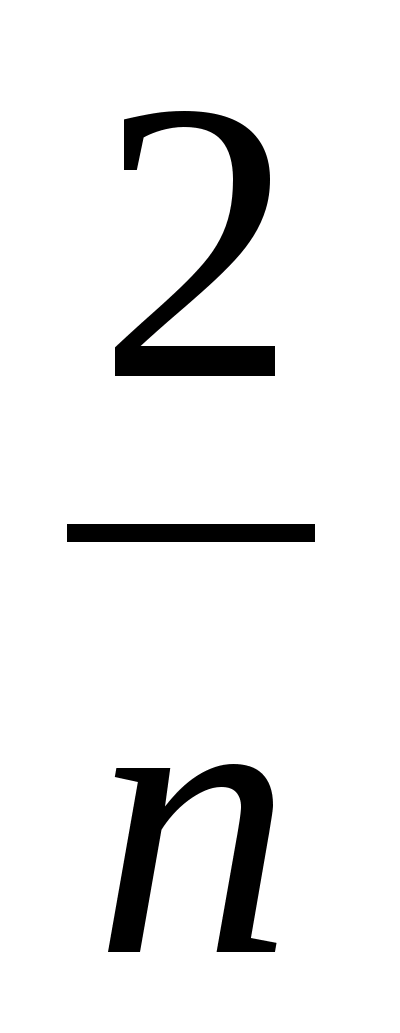 > 1. (6)
> 1. (6)
Так как n 3, m 3, то
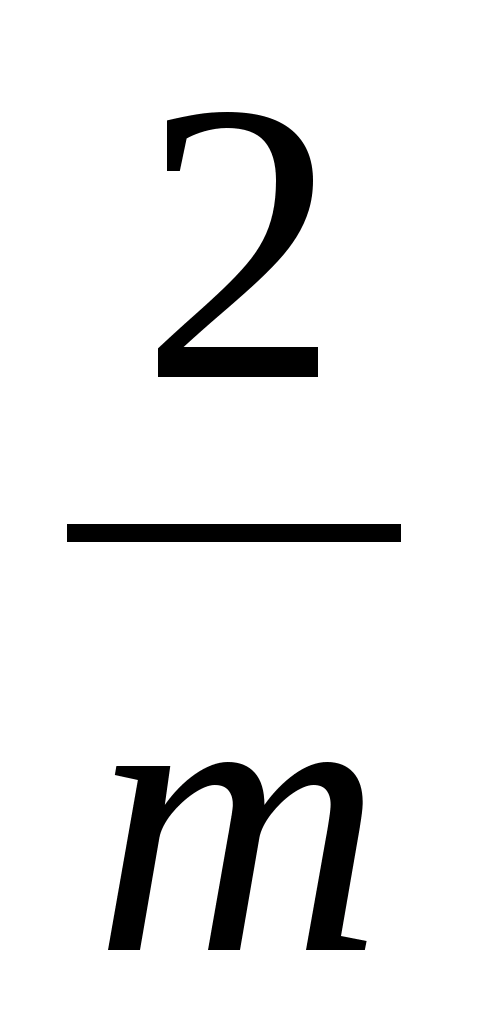 >
1 –
>
1 –
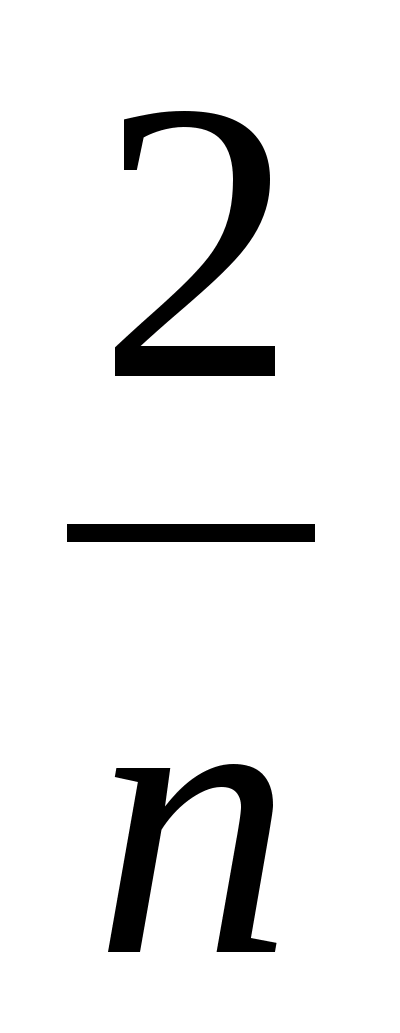
1 –
1 –
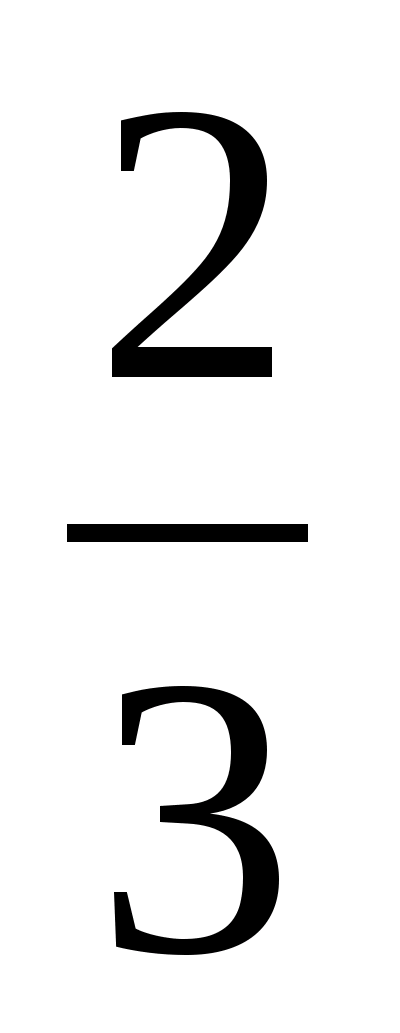 =
=
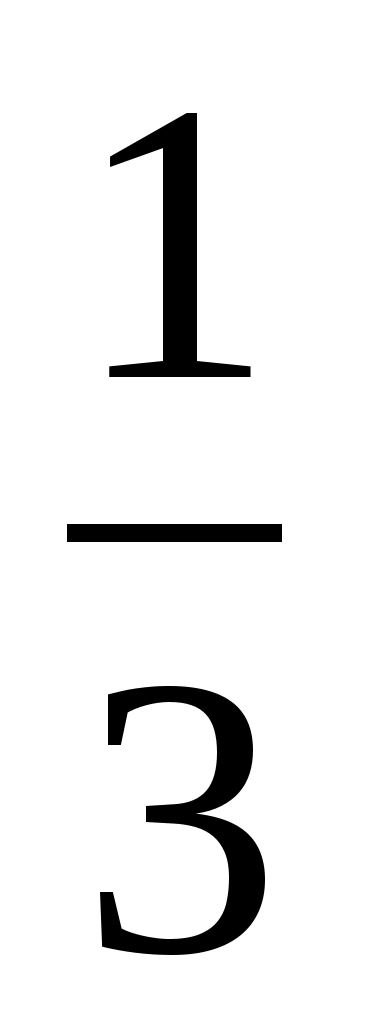 ,
,
что дает нам интервал значений для m
3 m < 6.
Аналогично получаем интервал значений для n
3 n < 6.
Рассматривая всевозможные комбинации значений n и m и, учитывая равенства (4), (5) и (6), получим все топологически правильные многогранники. Набор таких многогранников соответствует, по названию, набору правильных многогранников евклидова пространства.
2.3 Ориентируемые и неориентируемые поверхности
2.3.1 Определение ориентируемых и неориентируемых поверхностей
Обобщим понятие триангуляции поверхности многоугольниками на поверхность с краем. Клеточное разбиение Т поверхности F с краем F называется триангуляцией F, если в Т граница каждой двумерной клетки t>i> T состоит из трёх различных одномерных клеток разбиения Т. При этом концы каждой одномерной клетки лежат в двух различных одномерных клетках разбиения Т. В этом случае, нульмерные клетки триангуляции Т называются её вершинами, одномерные клетки – рёбрами, а двумерные клетки с границами – топологическими треугольниками (ниже термин «топологический» часто опускается).
То, что каждая поверхность с краем может быть триангулирована, доказал Тибор Радо. Отметим, что доказательство этого результата существенно опирается на наличие счётного базиса на поверхности. Без этого условия триангулируемости может и не быть – построены соответствующие примеры.
Пусть – ребро триангуляции Т поверхности с краем F с концами в точках А и В. Ориентацией ребра называется порядок в паре его вершин. Ребро имеет две ориентации (А, В) и (В, А). Их называют противоположными. Ребро называется ориентированным, если выбрана одна из двух его ориентаций.
Рассмотрим теперь топологический треугольник t Т с вершинами А, В и С. Ориентацией (или обходом) треугольника t называется порядок в тройке его вершин, причём ориентации считаются одинаковыми (эквивалентными), если они получаются друг из друга в результате циклической перестановки:
(А, В, С) (В, С, А) (С, А, В) и (С, В, А) (В, А, С) (А, С, В). Итак, треугольник t имеет две ориентации.
Определение 1. Треугольник называется ориентированным, если выбрана его ориентация.
Ориентация треугольника t порождает (индуцирует) ориентацию каждой из его сторон следующим образом: надо взять тот порядок его вершин из эквивалентных друг другу порядков, где обе вершины выбранной стороны стоят на первых двух местах, и отбросить третью вершину – оставшиеся две упорядоченные точки определяют ориентацию стороны, индуцированную ориентацией треугольника.
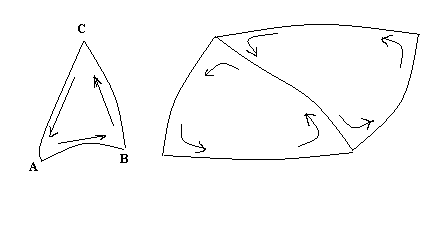
Определение 2. Говорят, что два ориентированных соседних треугольника в Т имеют согласованные ориентации, если на общей стороне они индуцируют противоположные ориентации.
метрический пространство топологический замкнутый
Определение 3. Поверхность с краем F называется ориентируемой, если существует такая ее триангуляция Т, все треугольники которой можно ориентировать так, что ориентации любых двух соседних треугольников согласованы.
Если такой ориентации не существует, то поверхность с краем называется неориентируемой.
Замечание. Можно доказать, что понятие ориентируемости поверхности не зависит от выбранной конкретной триангуляции и является топологическим инвариантом.
К числу поверхностей F с краем мы причисляем и поверхности без края, считая F = .
Пример 1. Евклидова плоскость Е2 и сфера S2 ориентируемы.
Действительно, это легко показать, непосредственно выполнив триангуляцию и выбрав согласованные ориентации.
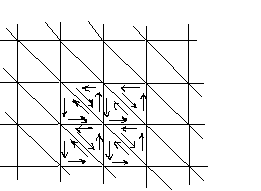
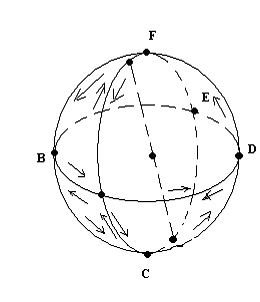
Пример 2. Лист Мёбиуса – неориентирован.
Разобьем прямоугольник АВСД на три треугольника и непосредственно убеждаемся в несогласованности этих треугольников разбиения.
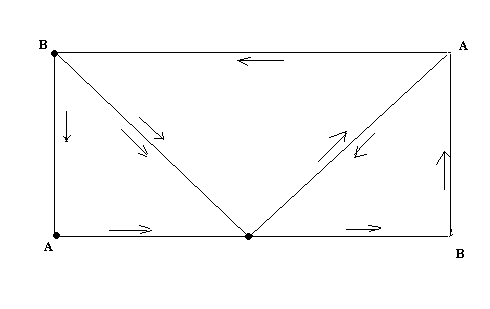
Пример 3. Бутылка Клейна – неориентирована.
Если в квадрате U2 = {(x, y)| 0 x 1, 0 y 1} считать эквивалентными точки вида (х, 0) и (1-х, 1), а также точки (0, у) и (1, у), то поверхность, склеенная из U2 по этому отношению эквивалентности, является неориентируемой замкнутой поверхностью, которая называется «бутылкой Клейна».
Мы отмечали ранее, что лист Мёбиуса дает нам, разумеется, наглядное описание односторонней поверхности с помощью «окрашивания». Однако, такое возможно лишь для «толстой поверхности», изготовленной из некоторого материала. Математическая поверхность не имеет толщины.
Поэтому подойдем к этому вопросу несколько иначе. В каждой точке a листа Мебиуса проведем два противоположных вектора, перпендикулярные к нему в этой точке. Эти векторы называются нормалями к листу Мебиуса в точке a.
Выберем одну из них и начнем перемещать точку a вместе с нормалью по ленте Мебиуса. Когда точка a обойдет всю ленту Мебиуса, то перемещающаяся нормаль при этом перейдет не в свое первоначальное положение, а в противоположное.
Итак, на ленте Мебиуса существует такой замкнутый путь (обход), что при прохождении этого пути нормаль к поверхности приходит в положение, противоположное первоначальному. Поверхности, обладающие такими обходами, и называются односторонними.
Однако, говоря о нормалях, мы изучаем не только саму поверхность, но и ее расположение в пространстве. Поэтому приведем «внутреннее» определение односторонних поверхностей. Условимся вокруг точки a, из которой проведена нормаль, описывать небольшую окружность и на ней отмечать стрелкой направление, которое из конца проведенной нормали наблюдается как направление против часовой стрелки. Если точка a перемещается, то вместе с ней перемещается и нормаль, а также окружность с имеющимся на ней направлением. Когда мы обведем окружность по всей ленте Мебиуса, направление изменится на противоположное (так как нормаль изменит свое направление).
Итак, на ленте Мебиуса имеется такой замкнутый путь (обход), что при перемещении окружности вдоль этого пути направление на окружности меняется на противоположное. Такие обходы называют обращающими ориентацию.
Если на поверхности нет обращающих ориентацию обходов, то она называется ориентируемой (или двусторонней), если есть неориентируемой (или односторонней). С наглядной точки зрения ориентируемость означает, что всю поверхность можно покрыть маленькими окружностями и выбрать на них такие направления, что близкие окружности будут ориентированы одинаково.
2.3.2 Классификация замкнутых поверхностей
Мы подходим к формулировке замечательной теоремы о топологической классификации поверхностей, полученной немецким математиком Мебиусом и французским математиком Жорданом.
Условимся рассматривать только замкнутые поверхности (которые не имеют края и допускают разбиение на конечное число многоугольников). Плоскость, например, не является замкнутой поверхностью: конечный граф, начерченный на плоскости, не разбивает ее на области, которые все гомеоморфны кругу.
Задача топологической классификации поверхностей заключается в том, чтобы указать такие попарно не гомеоморфные замкнутые поверхности, что любая замкнутая поверхность гомеоморфна одной из них. Иначе говоря, нужно перечислить все топологически различные замкнутые поверхности.
Теорема 1. Обозначим через P>0> сферу, а через P>k> сферу с k ручками. Тогда поверхности
P>0>, P>1>, P>2>, …, P>k>,… (1)
дают полную топологическую классификацию замкнутых ориентируемых поверхностей, т.е. здесь перечислены все различные типы таких поверхностей.
Замкнутую неориентируемую поверхность можно расположить в пространстве лишь с самопересечениями. Так как край ленты Мебиуса гомеоморфен окружности, то можно попытаться приклеить ленту Мебиуса своим краем к краю дыры, вырезанной в некоторой поверхности, например в сфере. Если на одной окружности кольца склеить между собой каждые две диаметрально противоположные точки, то мы получим ленту Мебиуса.
Пусть теперь ℓ контур круглой дыры на некоторой поверхности Q. Вырежем из поверхности узкую полоску (кольцо) вокруг дыры ℓ и обозначим через ℓ′ наружный контур этого кольца.
Тогда получится поверхность, гомеоморфная Q (только с несколько большей дырой ℓ′), и отдельно кольцо. Склеим теперь на контуре ℓ отрезанного кольца каждые диаметрально противоположные точки; тогда кольцо превратится в ленту Мебиуса. Эту ленту Мебиуса мы и вклеим в дыру ℓ′. В результате мы вклеим в поверхность Q (точнее, в поверхность, гомеоморфную ей) ленту Мебиуса. Но разрезание поверхности по контуру ℓ′ и обратное склеивание этого разреза можно было и не делать: достаточно было просто склеить на контуре ℓ каждые две диаметрально противоположные точки. Итак, склеивание каждых двух диаметрально противоположных точек на контуре круглой дыры равносильно вклеиванию в эту дыру ленту Мебиуса.
Теперь мы можем сформулировать вторую половину теоремы МебиусаЖордана о классификации поверхностей, а именно, дать перечисление всех топологически различных типов замкнутых неориентируемых поверхностей.
Теорема 2. Обозначим через N>q> поверхность, получающуюся из сферы вырезанием в ней q дыр и заклеиванием их всех лентами Мебиуса. Тогда поверхности
N>1>, N>2>, …, N>q>, … (2)
дают полную топологическую классификацию замкнутых неориентируемых поверхностей.
Заключение
Ответить на вопрос о том, что такое топология, весьма непросто. Известный французский математик Андре Вейль сказал, что за душу каждого математика борются ангел топологии и дьявол абстрактной алгебры, выразив этим, во-первых, необычное изящество и красоту топологии и, во-вторых, то, что вся современная математика представляет собой причудливое переплетение идей топологии и алгебры. А за последнее время топология все более проникает в физику, химию, биологию. Однако проникновение в волшебный мир топологи затруднительно. Подобно тому, как строительные леса, окружающие недостроенное здание, мешают охватить взглядом красоту архитектурного замысла, так многочисленные и утомительные детали построения, заполняющие книги по топологии, затрудняют охватить мысленным взором красивое здание этой математической науки. Даже многие специалисты – математики нередко отступают перед трудностями на пути овладения топологией. Для того чтобы в полной мере оценить задачи, которые решаются этой научной дисциплиной, необходимо серьезное изучение многих весьма сложных вопросов математики.
В ходе данной работы были рассмотрены основные элементы общей топологии.
Список использованной литературы
Александров А.Д., Нецветаев Н.Ю. Геометрия. – М.: Наука, 1990. –672 с.
Аминов Ю.А. Дифференциальная геометрия и топология кривых. – М.: Наука, 1987. –160 с.
Атанасян Л.С., Базылев В.Т. Геометрия. Ч. 2. – М.: Просвещение, 1987. – 351 с.
Болтянский В.Г., Ефремович В.А. Наглядная топология. – М.: Наука, 1982. – 148 с.
Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учеб. пособие. – М.: Высшая школа, 2005.
Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциаль-
ной геометрии. – М.: Просвещение, 1985. – 113 с.
Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: Наука, 1981. – 352 с.
Долженков В.А., Соловьева Е.Г., Горчинский И.В. Элементы общей топологии: Учеб.-метод. пособие − Курск: Курск. гос. ун-т, 2006. – 63 с.
Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. – М., 2004. – 464 с.
Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии: Учебник для университетов. – М.: Наука, 1987. – 432 с.
Рохлин В.А., Фукс Д.Б. Начальный курс топологии. М.: Наука, 1977. – 488 с.
Погорелов А.В. Геометрия. – М.: Наука, 1983. – 288 с.
13. Шварц Дж. Дифференциальная геометрия и топология. Новокузнецк: НФМИ, 2000.
14. Шашкин Ю.А. Эйлерова характеристика. М.: Наука, 1984. – 96 с.
15. Фоменко А.Т. Дифференциальная геометрия и топология. Дополнительные главы. – М.: Изд-во Моск. ун-та, 1983. – 216 с.
16. Энгелькинг Р. Общая топология. – М.: Мир, 1986.