Зависимость потребления бензина от количества автомобилей
Кафедра высшей математики
Курсовая работа
по теории вероятностей и математической статистике
на тему:
« Зависимость потребления бензина от количества автомобилей »
Дубна, 2003
Оглавление
ВВЕДЕНИЕ
ПОСТАНОВКА ЗАДАЧИ
ДИАГРАММА РАССЕИВАНИЯ
ПОСТРОЕНИЕ ПРЯМОЙ Y=AX+B, НАИМЕНЕЕ ОТКЛОНЯЮЩЕЙСЯ ОТ ТОЧЕК (XI;YI)В СРЕДНЕМ КВАДРАТИЧНОМ
ПОСТРОЕНИЕ КРИВОЙ Y=PX2+QX+R, НАИМЕНЕЕ ОТКЛОНЯЮЩЕЙСЯ ОТ ТОЧЕК (XI;YI) В СРЕДНЕМ КВАДРАТИЧНОМ
АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ И ВЫВОД О ЗАВИСИМОСТИ XI И YI
ВЫВОД
СПИСОК ЛИТЕРАТУРЫ
Введение
В данной работе исследуется зависимость потребления бензина в городе от количества автомобилей с помощью методов математической статистики.
Бензин – смесь легких углеводородов с t>кип> 30-205 °C; прозрачная жидкость, плотность 0,70-0,78 г/см3. Получают главным образом перегонкой или крекингом нефти. Топливо для карбюраторных авто- и авиадвигателей; экстрагент и растворитель для жиров, смол, каучуков.
Автомобиль – транспортная безрельсовая машина главным образом на колесном ходу, приводимая в движение собственным двигателем (внутреннего сгорания, электрическим или паровым). Различают автомобили пассажирские (легковые и автобусы), грузовые, специальные (пожарные, санитарные и др.) и гоночные. Скорость легковых автомобилей до 300 км/ч, гоночных до 1020 км/ч (1993), грузоподъемность грузовых автомобилей до 180 т.
Обычно в любой области науки при изучении двух величин проводятся эксперименты, и задача состоит в том, чтобы на основании экспериментальных точек выявить функциональную зависимость.
Если мы рассматриваем слабо формализованные системы, которые трудно поддаются однозначным и точным описаниям, связь между величинами X и Y изначально корреляционная. Это связано, что Y зависит не только от X, но и от других параметров.
В этом случае, задача состоит в том, чтобы приближённо свести корреляционную связь к функциональной с помощью подбора такой функции, которая максимально возможным способом была бы близка к экспериментальным точкам. Такая функция называется функцией регрессии.
Обычно вид самой функции угадывается, но она зависит от некоторых параметров. Задача статистического и корреляционного анализа состоит в нахождении этих параметров. Для этого и используется метод наименьших квадратов.
Постановка задачи
Даны выборки
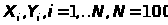
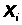 – количество автомобилей,
– количество автомобилей,
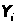 – потребление бензина.
– потребление бензина.
Задача состоит в изучении
характера зависимости
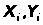
1. Изобразить точки (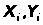 )
на плоскости (на миллиметровой бумаге
и в виде точечного графика на компьютере)
)
на плоскости (на миллиметровой бумаге
и в виде точечного графика на компьютере)
2. Методом наименьших
квадратов определить числа
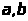 такие, что прямая
такие, что прямая
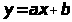 наименее уклоняется от точек (
наименее уклоняется от точек (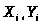 )
в среднем квадратичном.
)
в среднем квадратичном.
3. Методом наименьших
квадратов определить числа
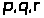 такие, что парабола
такие, что парабола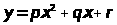 наименее уклоняется от точек (
наименее уклоняется от точек (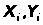 )
в среднем квадратичном.
)
в среднем квадратичном.
4. Сравнить между собой результаты пунктов 2. и 3.
5. С помощью сравнения
статистик
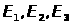
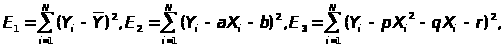
где
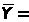
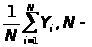 объем выборки, ответить на вопросы:
объем выборки, ответить на вопросы:
1) Подтвердилась ли гипотеза
о том, что зависимость между
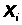 и
и
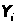 близка к линейной ?
близка к линейной ?
2) Подтвердилась ли гипотеза
о том, что зависимость между
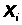 и
и
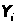
близка к квадратичной?
3) Какая из двух кривых -
прямая или парабола - меньше отклоняется
от точек выборки (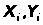 )
?
)
?
Диаграмма рассеивания
Даны
выборки
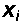 и
и
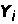 ,
которые можно интерпретировать следующим
образом:
,
которые можно интерпретировать следующим
образом:
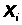 —
потребление бензина,
—
потребление бензина,
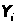 — количество автомобилей. Задача состоит
в изучении характера зависимости между
— количество автомобилей. Задача состоит
в изучении характера зависимости между
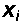 и
и
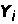 .
Исходные выборки представлены в таблице:
.
Исходные выборки представлены в таблице:
-
X
Y
X
Y
X
Y
X
Y
8,64558
116,76
22,2483
112,8
35,3723
113,328
48,6586
125,396
9,30954
115,72
22,38
114,03
35,8685
119,397
49,2468
126,783
9,54538
109,996
22,743
114,952
36,0494
124,624
49,0515
125,652
9,91695
126,634
23,0127
117,027
36,5302
118,734
49,7645
119,88
10,3459
112,28
23,9216
110,664
36,7256
126,531
50,6983
129,604
11,1794
115,564
24,7213
120,474
37,2568
125,601
50,4538
125,877
12,0403
116,048
25,2151
120,749
38,6184
121,974
51,7368
124,935
12,4383
114,524
25,5633
125,365
38,669
123,196
52,3859
121,572
12,8887
114,716
26,5224
117,494
39,2617
119,925
52,932
127,416
13,3673
107,328
26,654
112,982
40,1783
122,293
53,1557
123,507
13,5643
114,422
26,7975
112,34
40,239
120,465
54,0261
128,29
14,4435
118,925
27,6272
127,172
41,1804
122,419
54,4972
136,727
14,4909
123,297
28,2653
121,229
40,8874
127,014
54,3892
125,732
15,3408
119,606
28,6799
119,246
42,0704
133,402
55,475
124,107
15,5866
116,443
28,9424
113,728
42,7372
136,142
55,7691
128,79
16,9966
119,384
29,8652
124,189
42,8423
123,36
55,912
139,417
17,4323
116,428
30,2303
131,775
43,6994
128,363
56,6281
127,151
17,2341
123,058
30,6092
113,164
44,4041
118,225
57,6097
130,697
17,7988
116,349
31,6162
122,517
45,0372
126,604
57,3441
142,839
18,5831
116,665
32,1788
117,256
45,1258
127,831
58,699
134,079
19,4722
118,844
32,7243
114,794
45,4427
122,39
59,0407
130,316
19,8208
123,205
32,7933
130,624
46,3461
129,182
59,3109
129,148
20,6594
109,789
33,1236
133,529
46,5863
127,344
59,8175
135,398
20,8651
118,634
34,0453
123,582
47,3429
124,694
60,3217
131,061
21,0348
110,347
34,9061
135,169
47,7225
117,103
61,2562
126,388
Изобразим эти точки в
виде точечного графика с соответствующими
координатами (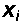 ,
,
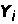 );
для этого надо найти размах выборки по
X
и Y
и выбрать соответствующий масштаб.
Сначала находим
);
для этого надо найти размах выборки по
X
и Y
и выбрать соответствующий масштаб.
Сначала находим
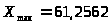 и
и
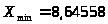 ,
затем размах выборки по X,
которая вычисляется по формуле
,
затем размах выборки по X,
которая вычисляется по формуле
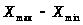 и в результате равна 52,61062. Аналогично
и в результате равна 52,61062. Аналогично
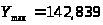 и
и
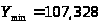 ,
а размах выборки поY
получим равный 35,511. Глядя
на размах выборок по X
и по Y,
выбираем масштаб диаграммы рассеивания
и строим её.
,
а размах выборки поY
получим равный 35,511. Глядя
на размах выборок по X
и по Y,
выбираем масштаб диаграммы рассеивания
и строим её.
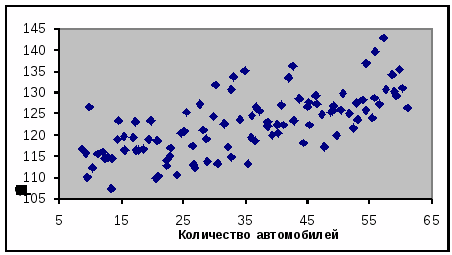
рис.1. Диаграмма рассеивания
По формуле
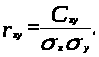 где
где

можно найти коэффициент корреляции:
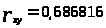
Он не равен нулю, следовательно, зависимость между X и Y существует.
Построение прямой y=ax+b, наименее отклоняющейся от точек (X>i>;Y>i>)в среднем квадратичном
Для построения прямой y
= ax + b, наименее отклоняющейся
от точек
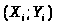 в среднем квадратичном, необходимо
методом наименьших квадратов определить
числа a,
b
такие, что функция двух переменных
в среднем квадратичном, необходимо
методом наименьших квадратов определить
числа a,
b
такие, что функция двух переменных
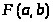 принимает минимальное значение. Данная
функция имеет вид:
принимает минимальное значение. Данная
функция имеет вид:
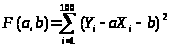 .
.
Зная, что необходимым
условием минимума функции является
равенство нулю ее первых частных
производных, имеем следующую систему
для нахождения значений
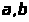 :
:
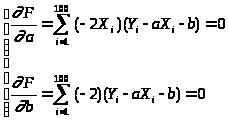 ,
,
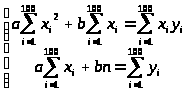
Данная система может быть представлена в виде:
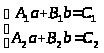 ,
,
где
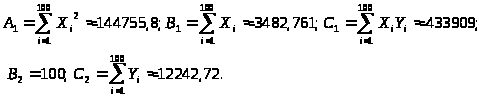
В результате получим что:
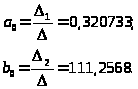
Докажем теперь, что в
точке
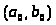 функция
функция
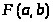 имеет минимум. Достаточным условием
существования экстремума функции двух
переменных является следующее неравенство:
имеет минимум. Достаточным условием
существования экстремума функции двух
переменных является следующее неравенство:
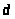
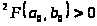 .
.
Для доказательства введем следующие обозначения:
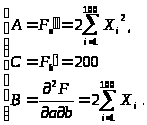
Составим
дискриминант
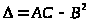 .
Тогда, если
.
Тогда, если
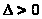 ,
то функция имеет в точке экстремум, а
именно минимум при А>0 (или С>0). Из
системы видно, что эти условия выполняются:
,
то функция имеет в точке экстремум, а
именно минимум при А>0 (или С>0). Из
системы видно, что эти условия выполняются:
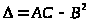 =
=
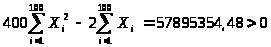 ,
С=200>0.
,
С=200>0.
То есть точка
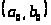 действительно является точкой минимума.
действительно является точкой минимума.
Следовательно, функция
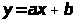 при данных значениях
при данных значениях
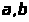 имеет следующий график:
имеет следующий график:
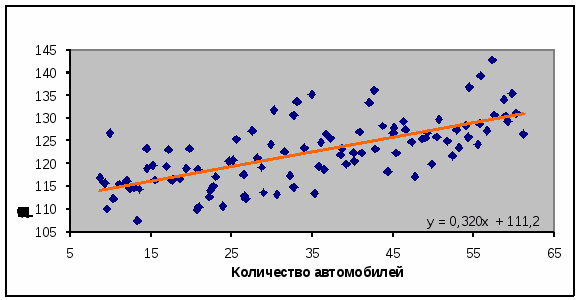
рис.2. График уравнения линейной регрессии
Построение кривой y=px2+qx+r, наименее отклоняющейся от точек (X>i>;Y>i>) в среднем квадратичном
Для построения
кривой
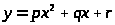 ,
наименее отклоняющейся от точек
,
наименее отклоняющейся от точек
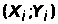 в среднем квадратичном, необходимо
методом наименьших квадратов определить
числа
в среднем квадратичном, необходимо
методом наименьших квадратов определить
числа
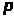 ,
,
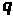 и
и
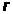 такие, что функция трех переменных
такие, что функция трех переменных
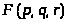 принимает минимальное значение. Данная
функция имеет вид:
принимает минимальное значение. Данная
функция имеет вид:
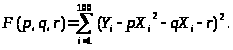
Аналогично
нахождению значений
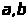 для прямой
для прямой
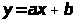 составляем систему трех линейных
уравнений, которая является необходимым
условием минимума функции:
составляем систему трех линейных
уравнений, которая является необходимым
условием минимума функции:
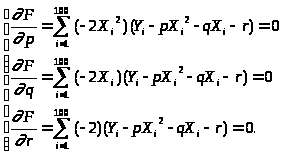
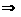
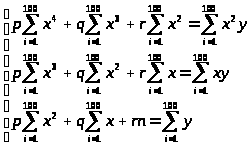
Данная система является системой линейных однородных уравнений. Решая эту систему методом Крамера и зная, что:
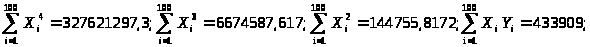
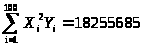
составляем определители,
состоящие из коэффициентов при
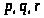 и столбца свободных членов.
и столбца свободных членов.
Значения
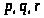 находим делением соответствующих
определителей.
находим делением соответствующих
определителей.
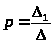 =
=
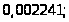
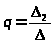 =
=
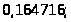
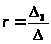 =
=
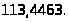
Докажем теперь, что в
точке
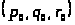 функция
функция
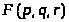 имеет минимум. Достаточным условием
существования минимума функции трех
переменных является следующее неравенство:
имеет минимум. Достаточным условием
существования минимума функции трех
переменных является следующее неравенство:
d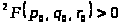 .
.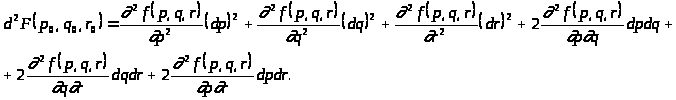
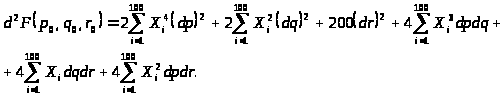
Получаем следующее уравнение:
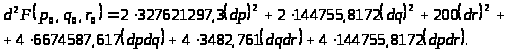
Воспользуемся критерием Сильвестра, т.е. найдем миноры 1-ого, 2-ого и 3-ого порядков и докажем, что они положительные.
 =
=
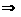
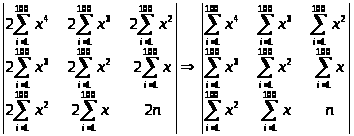 =
=
Найдем миноры первого, второго и третьего порядков для этого определителя:
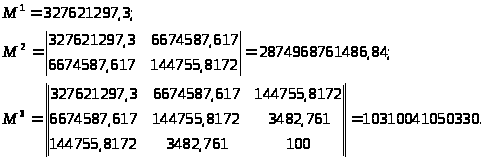
Так как все миноры
положительны, то по критерию Сильвестра
d ,
и функция
,
и функция
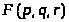 имеет минимум в точке
имеет минимум в точке
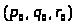 .
.
Таким образом, парабола
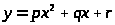 имеет следующий график:
имеет следующий график:
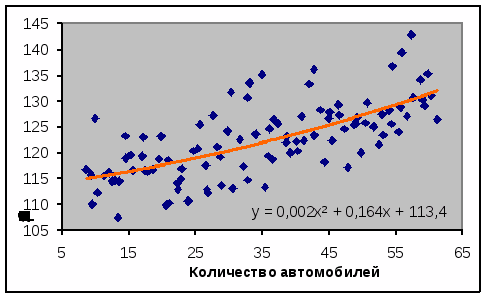
рис.3. График уравнения параболической регрессии
Анализ полученных результатов и вывод о зависимости X>i> и Y>i>
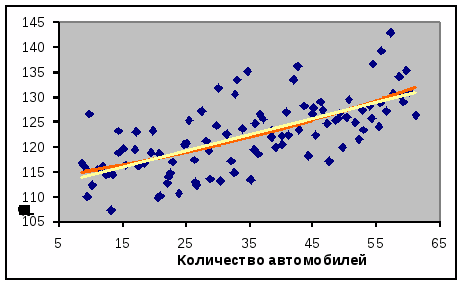
рис.4. Сравнение линейной и параболической регрессий
Для сравнения
полученных результатов построения
кривых
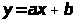 и
и
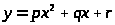 определим значения статистик:
определим значения статистик:
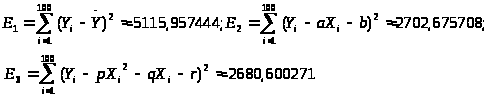
Поскольку
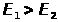 и
и
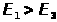 ,
можно говорить о том, что зависимость
между
,
можно говорить о том, что зависимость
между
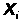 и
и
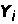 близка и к линейной, и к квадратичной.
При этом парабола
близка и к линейной, и к квадратичной.
При этом парабола
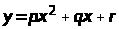 меньше отклоняется от точек
меньше отклоняется от точек
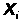 и
и
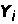 ,
чем прямая
,
чем прямая
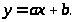
Вывод
Зависимость потребления бензина
от количества автомобилей близка к
линейной и к квадратичной. Однако видно,
что разница между значениями статистик
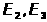 небольшая. Следовательно, с практической
точки зрения удобнее приближать точки
выборки
небольшая. Следовательно, с практической
точки зрения удобнее приближать точки
выборки
 и
и
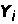 к прямой
к прямой
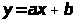 .
Выявление зависимости
между потреблением бензина и количеством
автомобилей пригодится для понимания
ситуации, которая складывается у нас
на дорогах и влияет на природу, поскольку
потребление бензина всегда сопровождается
вредными выбросами.
.
Выявление зависимости
между потреблением бензина и количеством
автомобилей пригодится для понимания
ситуации, которая складывается у нас
на дорогах и влияет на природу, поскольку
потребление бензина всегда сопровождается
вредными выбросами.
Список литературы
Гмурман В.Е. Теория вероятностей и математическая статистика. — М.: Высшая школа 1998.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике — М.: Высшая школа 1998.
Ивашев-Мусатов О. С. Теория вероятностей и математическая статистика — М.: Наука 1979.
Мазный Г.Л., Прогулова Т.Б. Методическое пособие к курсовому проектированию по ВМ и информатике. — Дубна: Кафедра ВМ и САУ, 1996.