Теория управления (работа 1)
1. Общая постановка задачи управляемости.
Для
задачи ОУ характерно наличие динамического
объекта. Динамический объект- объект,
состояние которого меняется со временем.
Состояние любого динамического объекта
в момент времени
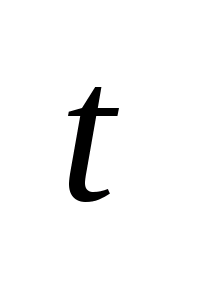 характеризуется
параметрами
характеризуется
параметрами
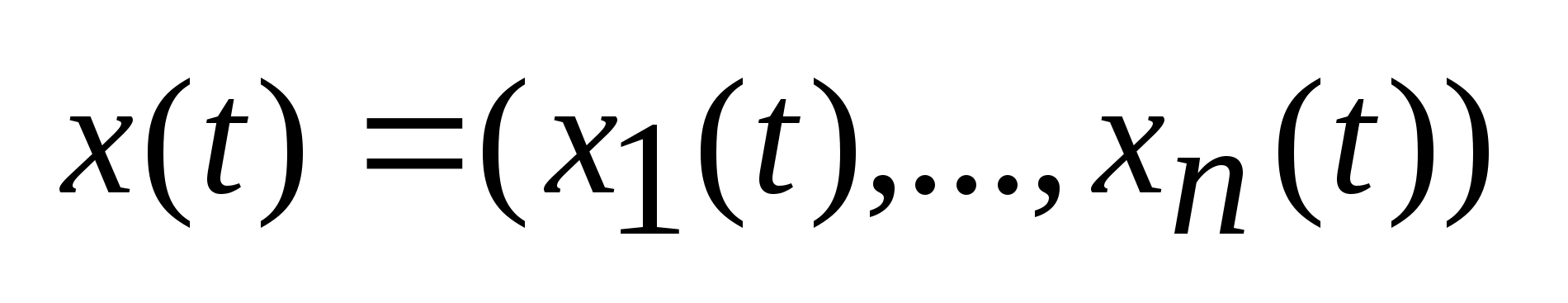 .
Такие параметры наз. Фазовые координаты,
а сам вектор- фазовый вектор.
.
Такие параметры наз. Фазовые координаты,
а сам вектор- фазовый вектор.
Предполагается,
что движением объекта можно управлять.
Набор параметров
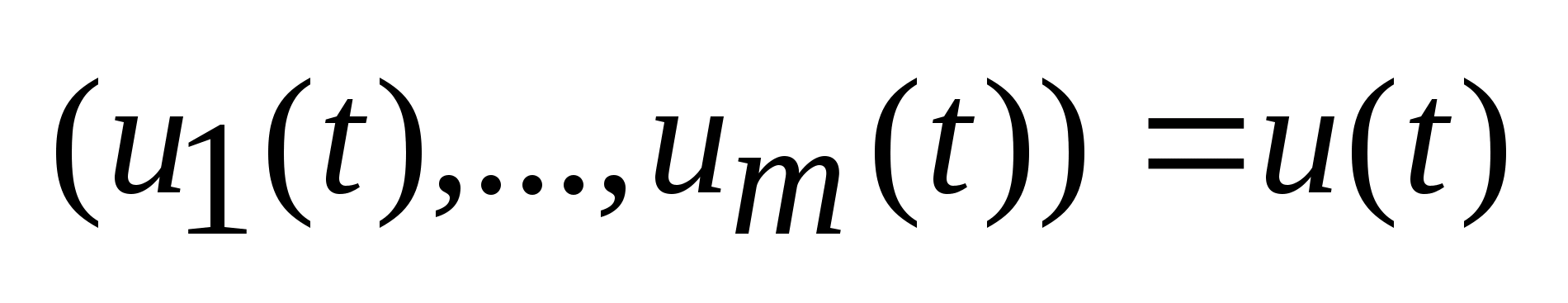 -
параметры управления, u(t)-
вектор управления. Положение объекта
зависит только от того, какое управление
было до момента времени
-
параметры управления, u(t)-
вектор управления. Положение объекта
зависит только от того, какое управление
было до момента времени
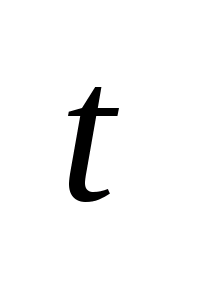 ,
и не зависит от того, какое управление
будет в будущем. В зависимости от описания
дин. Объекта рассматриваются различные
задачи.
,
и не зависит от того, какое управление
будет в будущем. В зависимости от описания
дин. Объекта рассматриваются различные
задачи.
Состояние динамического объекта описывается диф. уравнением
1)
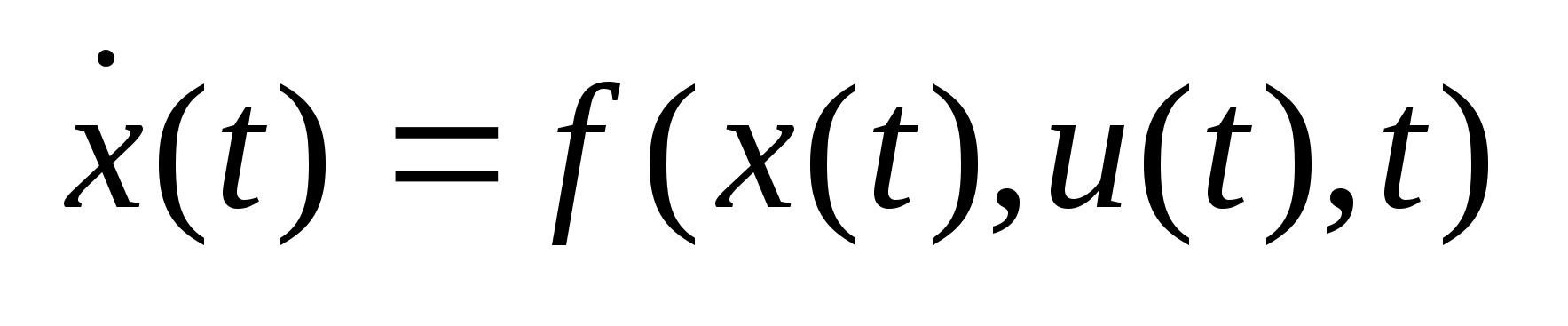 -
эта система решается приближенным
методом.
-
эта система решается приближенным
методом.
2)
x(t)
должны принадлежать
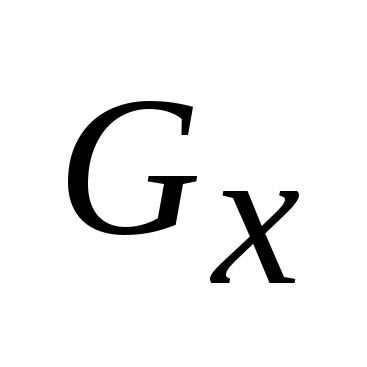 ,
,
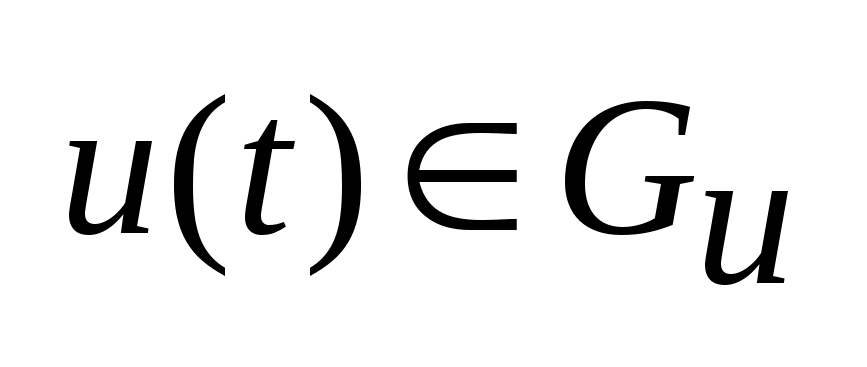 .
Класс допустимых управлений x(t),
.
Класс допустимых управлений x(t),
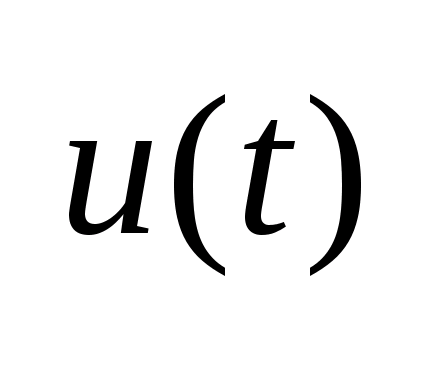 не
можат быть произвольным.
не
можат быть произвольным.
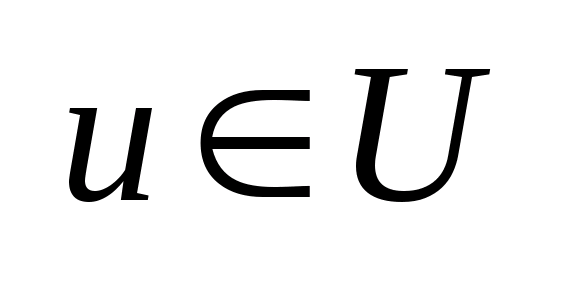 ,
как правило мн-во замкнуто и ограничено,
а это не позволяет применять класс
вариационого исчесления, кроме этого
на
,
как правило мн-во замкнуто и ограничено,
а это не позволяет применять класс
вариационого исчесления, кроме этого
на
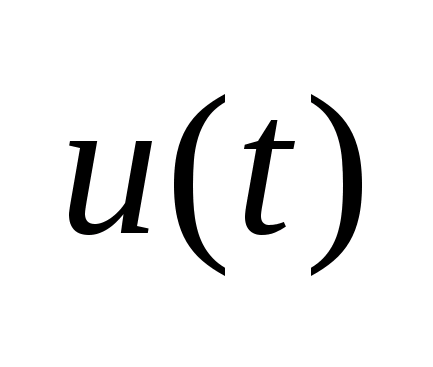 могут
быть наложены ограничения по времени.
могут
быть наложены ограничения по времени.
3)Начальное
и конечное состояние объекта.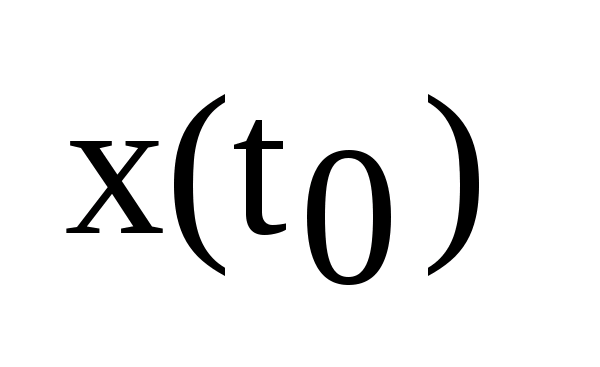 на
интервале
на
интервале
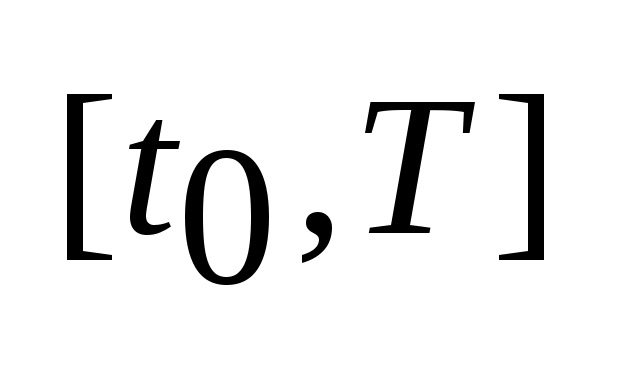 ,
,
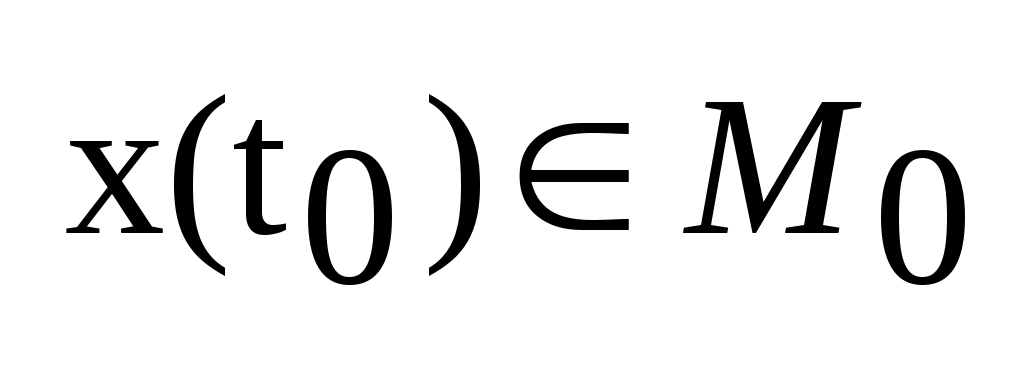 ,
,
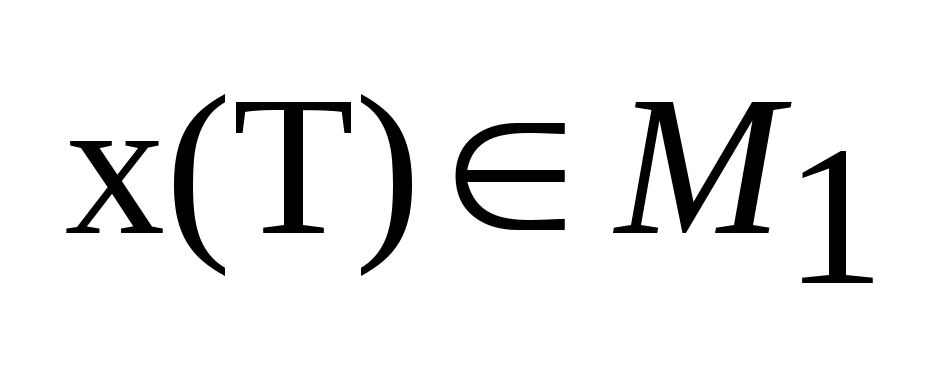 .Задача
управления заключается в том, чтобы
динамический
объект, описываемый системой (1),
удовлетворяющий условиям (2), перенести
за промежуток времени
.Задача
управления заключается в том, чтобы
динамический
объект, описываемый системой (1),
удовлетворяющий условиям (2), перенести
за промежуток времени
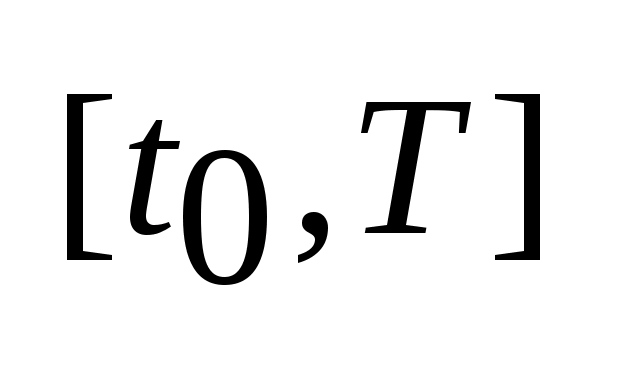 ,
из состояния
,
из состояния
 .Это
может быть достигнуто разными способами.
.Это
может быть достигнуто разными способами.
4)
Критерий управления. Это некоторый
функционал вида
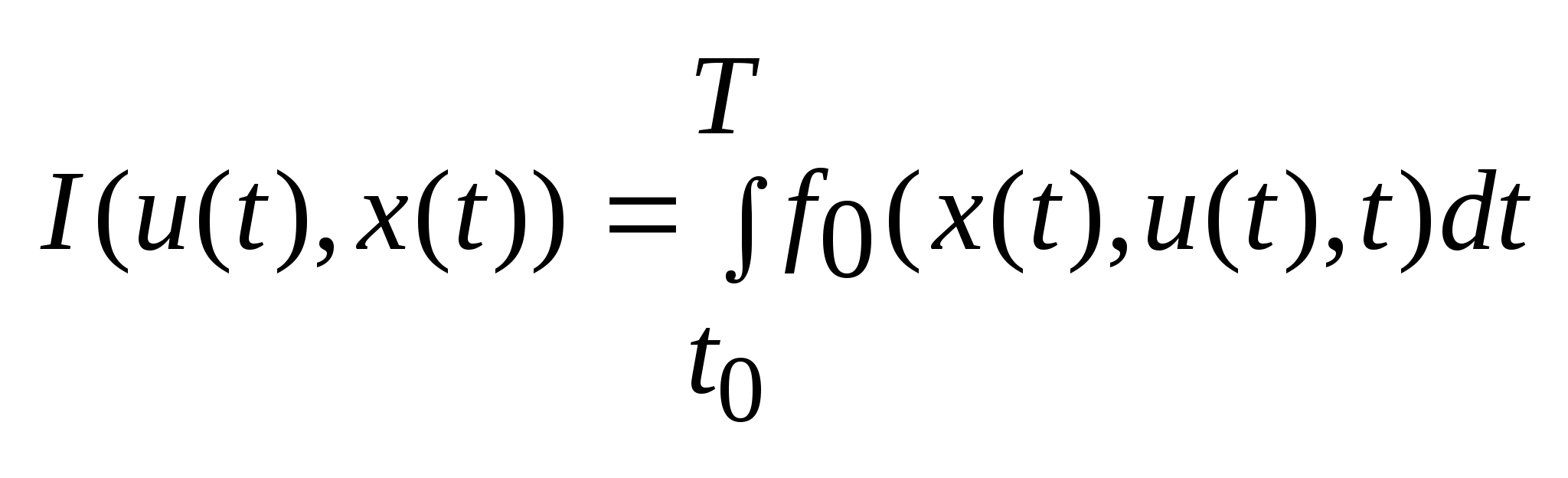 .
Находим такие
.
Находим такие
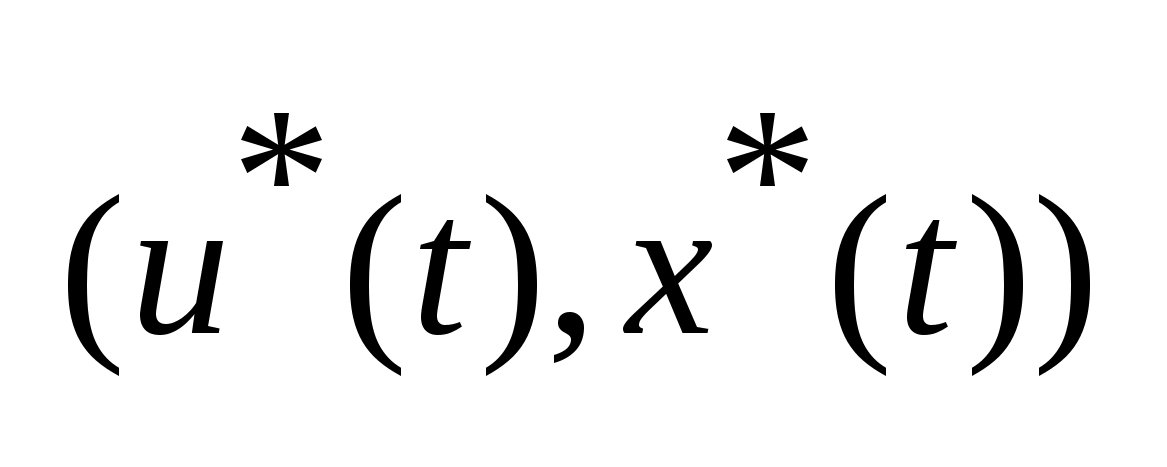 ,
что
,
что
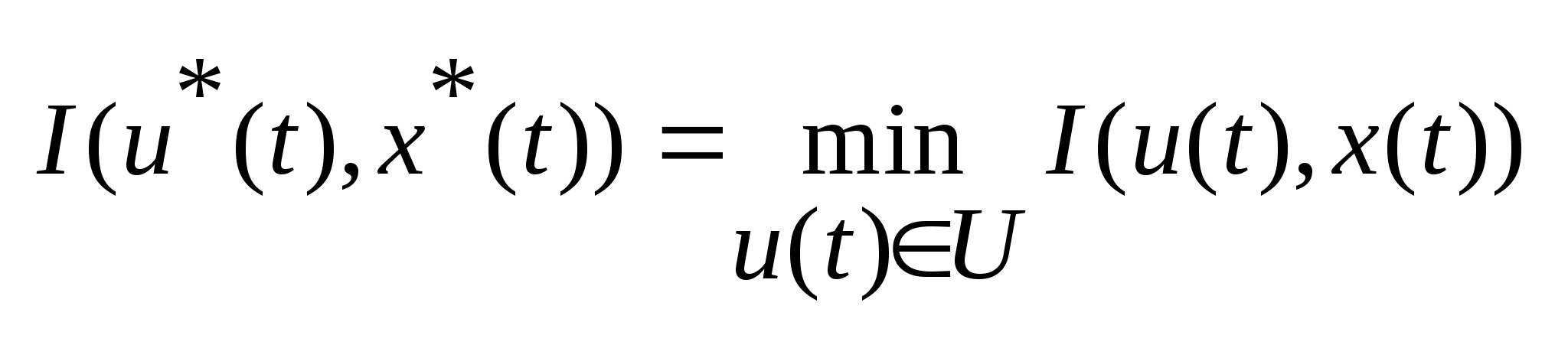
2. Основные вопросы в теории ОУ.
1) Управляемость. Можно ли осуществить перевод динамического объекта из состояния
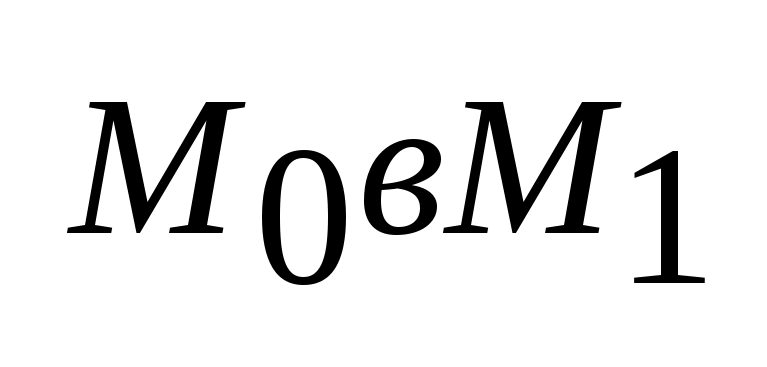 ,
за промежуток времени
,
за промежуток времени
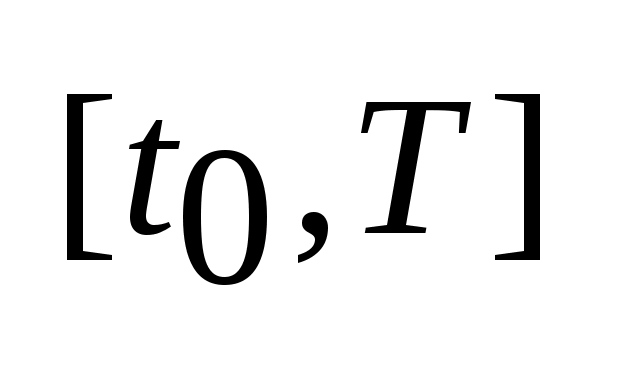 .
.Существует ли ОУ.
3) Необходимые условия оптимальности- принцип максимума Понтрягина.
4) Достаточные условия ОУ.
5) Единственность ОУ.
3. Постановка линейной задачи.
Линейная
задача имеет вид: Рассматриваем
динамический объект, поведение которого
описывается системой (1)
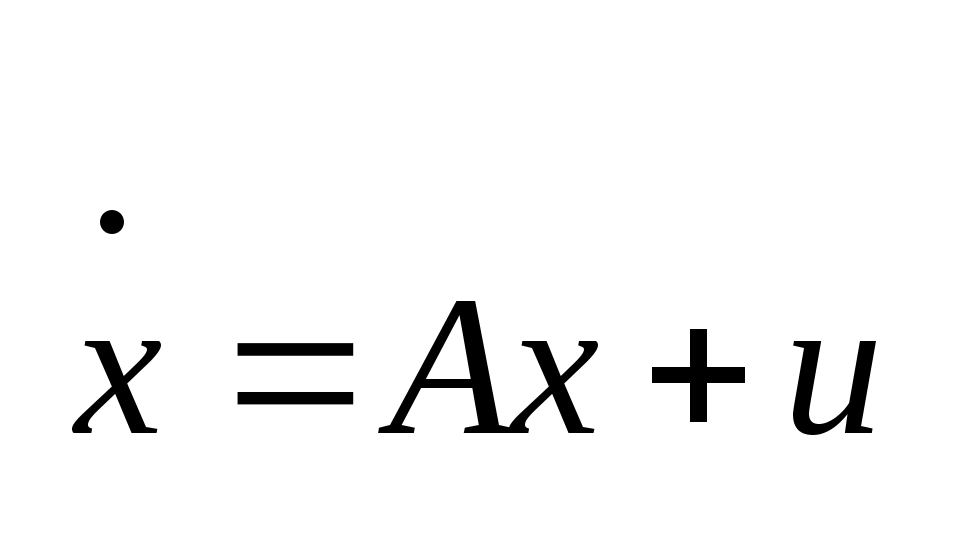 ,
x-
n-мерный
вектор, , A-матрица
nxn,
u
имеет ту же размерность,
что
и
,
x-
n-мерный
вектор, , A-матрица
nxn,
u
имеет ту же размерность,
что
и
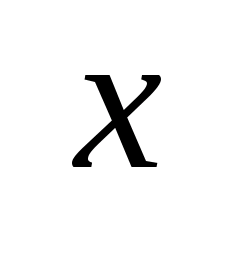 ,
,
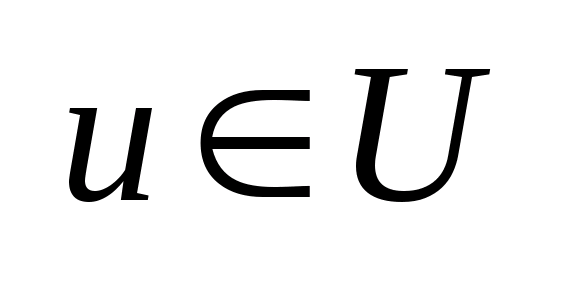 ,
,
 -замкнуто
и ограничено.
Допустимое управление u(t)
на отр.I
осуществляет
переход из начального мн-ва
-замкнуто
и ограничено.
Допустимое управление u(t)
на отр.I
осуществляет
переход из начального мн-ва
 в конечное множество
в конечное множество
 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
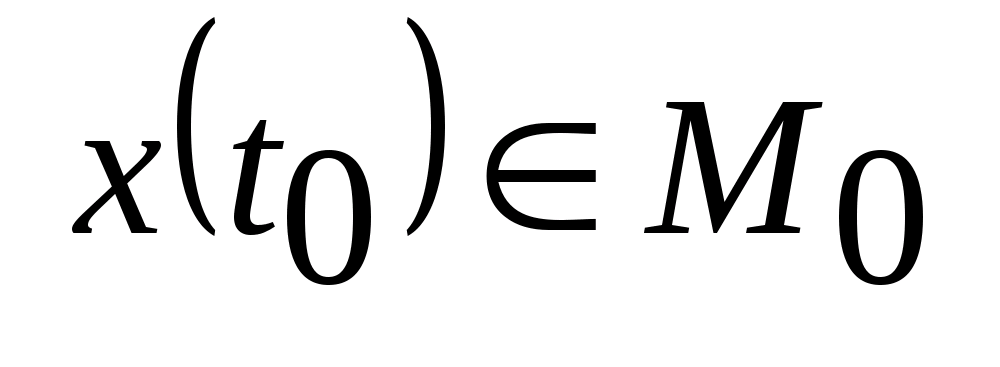 и
и
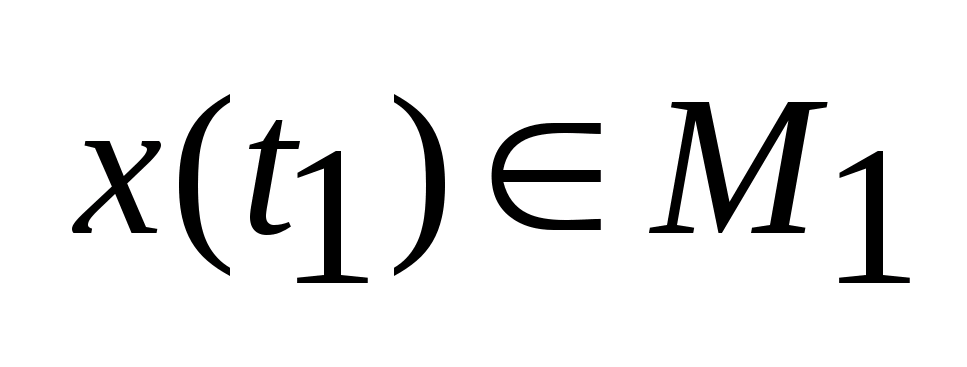 .
Цель управления
-
перевод динамический объекта из
.
Цель управления
-
перевод динамический объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача быстродействия заключается в
нахождении такого допустимого управления,
которое осуществляет переход из множества
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача быстродействия заключается в
нахождении такого допустимого управления,
которое осуществляет переход из множества
 в
в
 за
наименьшее время.
за
наименьшее время.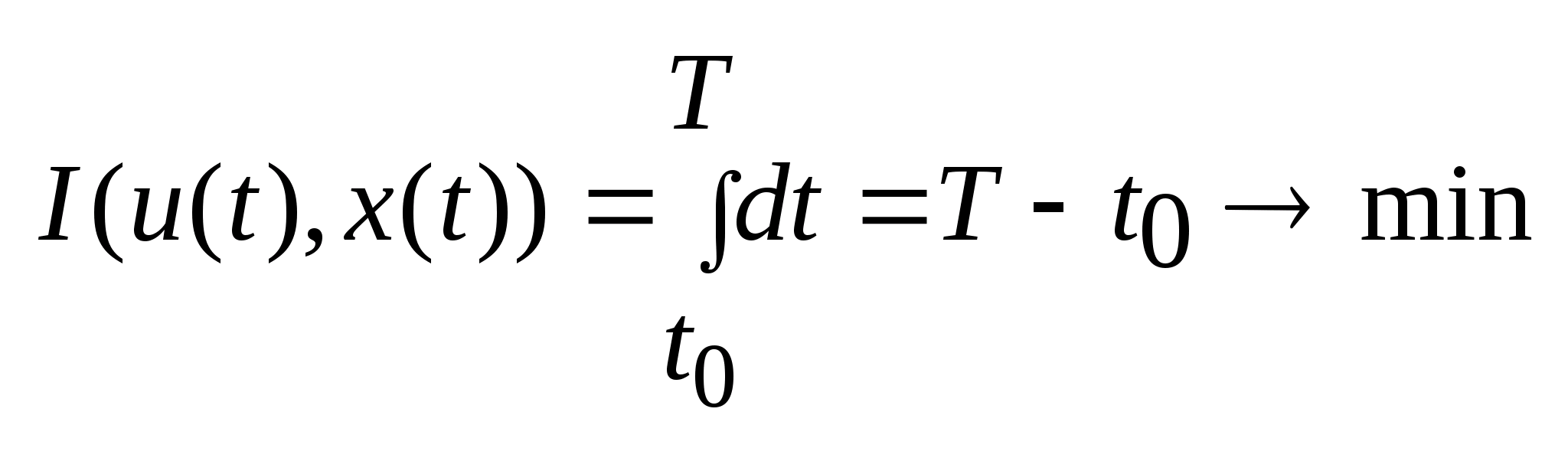
4.
Пространство
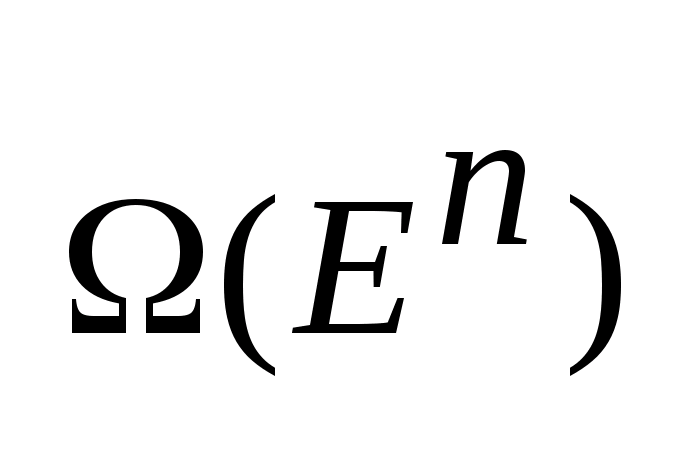 ,
алгебраическая сумма
,
алгебраическая сумма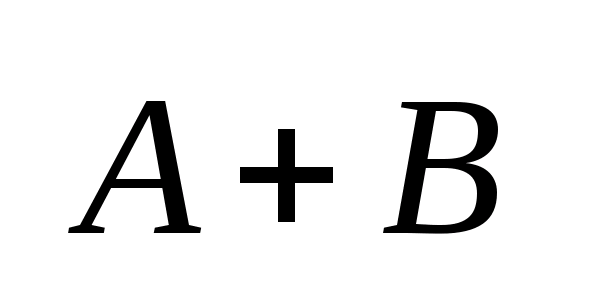 ,
произведение множества на число
,
произведение множества на число
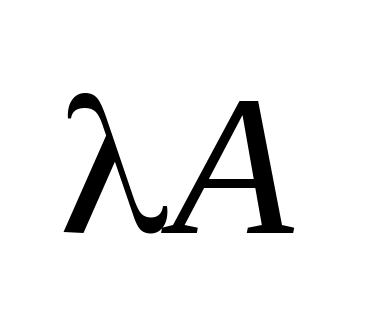 .
.
Пространство
 -пространство
состоящее из всевозможных не пустых
компактных подмножеств пр-ва
-пространство
состоящее из всевозможных не пустых
компактных подмножеств пр-ва
 .
.
Мн-во F компактное, если оно замкнуто и ограничено.
Мн-во F ограничено, если оно содержится в шарк некоторого радиуса.
Мн-во F замкнуто, если оно содержит все свои предельные точки.
Точка f предельная точка F, если в любой ее окрестности содержится хотя бы одна точка мн-ва F отличная от f.
Операции:1)
алгебраической суммой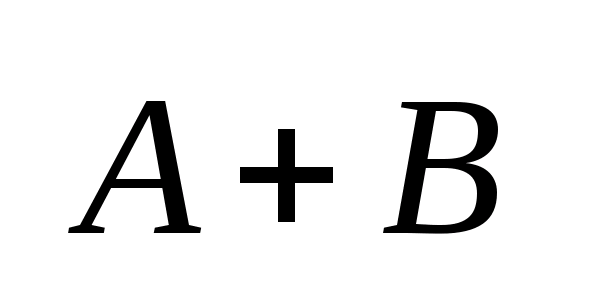 наз.
мн-во C
такое, что любой элемент
наз.
мн-во C
такое, что любой элемент
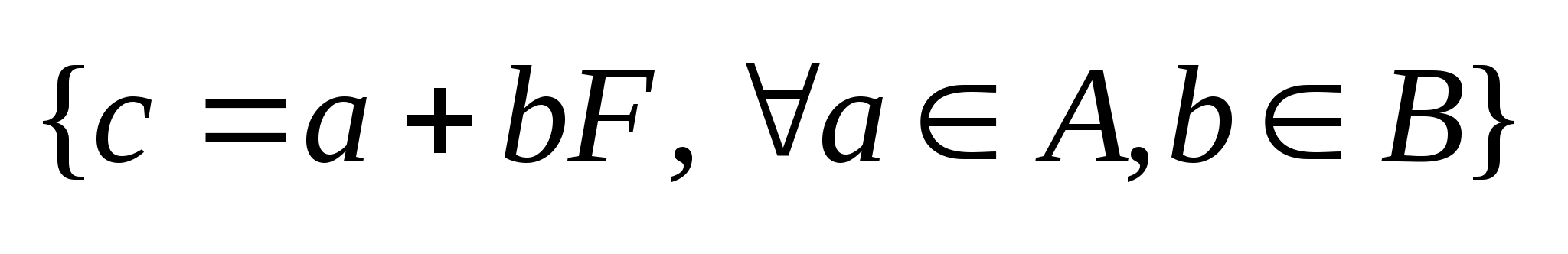 ,
,
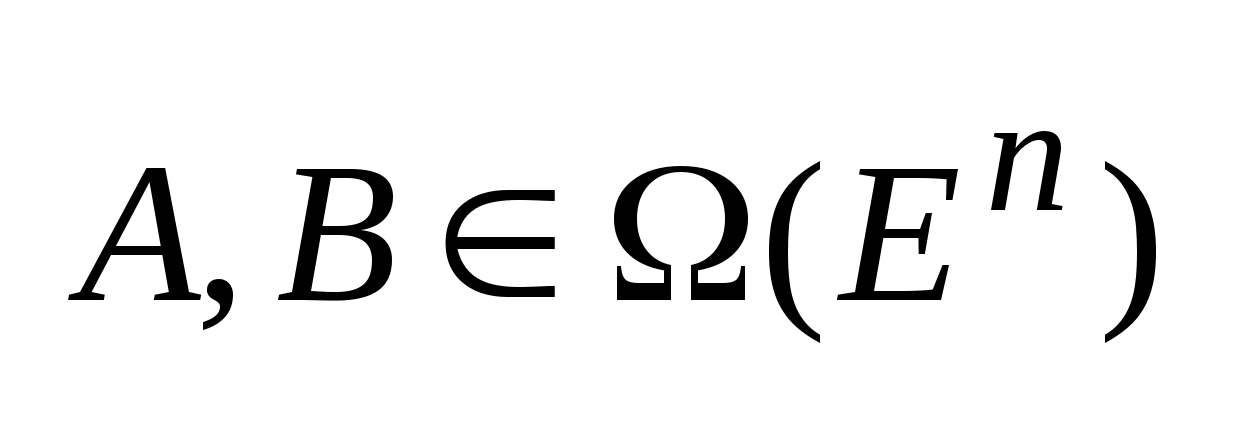
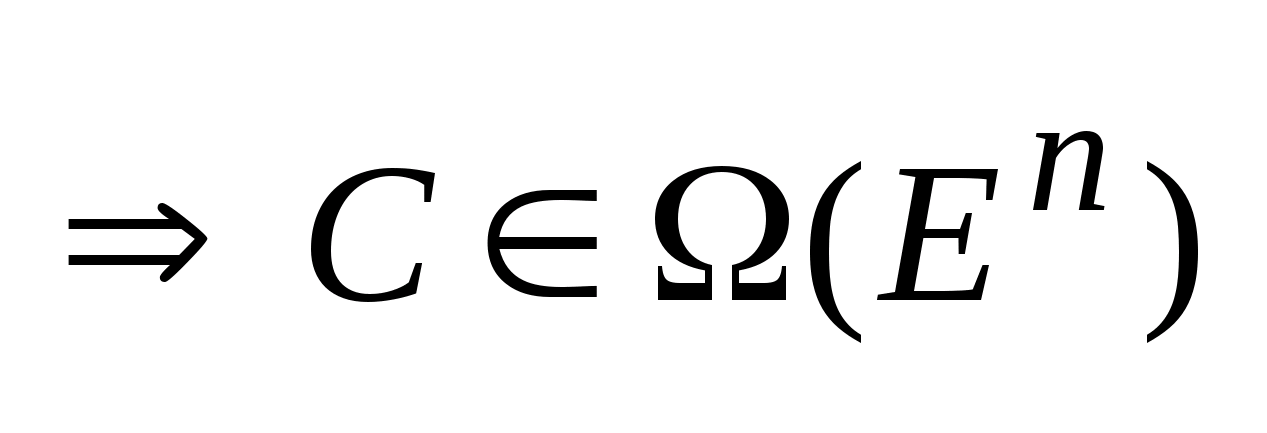 .
.
2)
произведением множества на число
 наз. мн-во C
такое, что любой элемент
наз. мн-во C
такое, что любой элемент
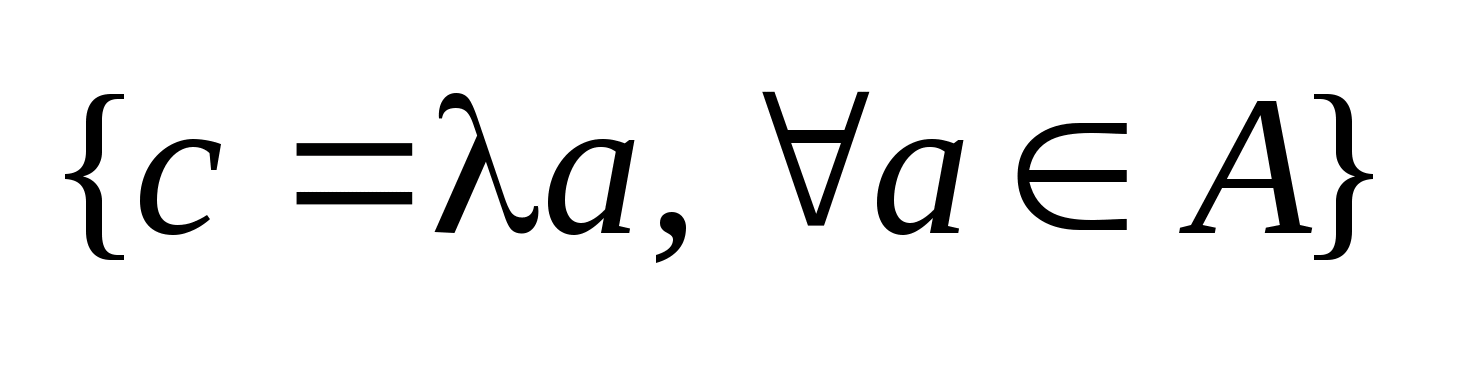 .
.
5.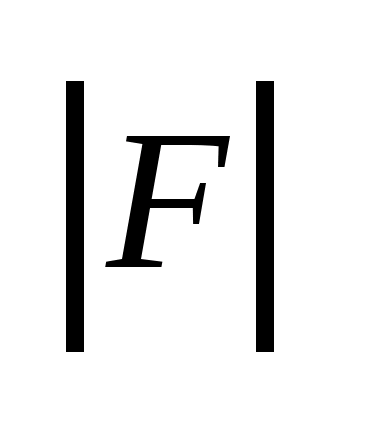 ,
хаусдорффова
норма, лемма про определенность хаус.
нормы.
,
хаусдорффова
норма, лемма про определенность хаус.
нормы.
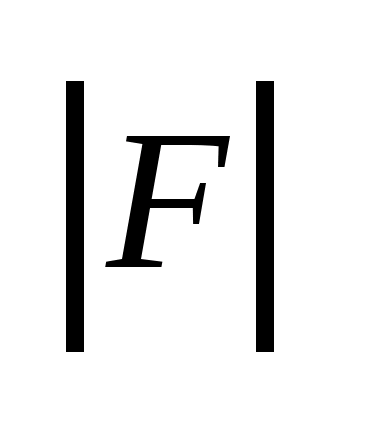 -это
минимальный радиус шара с центром в
начале координат, где
-это
минимальный радиус шара с центром в
начале координат, где
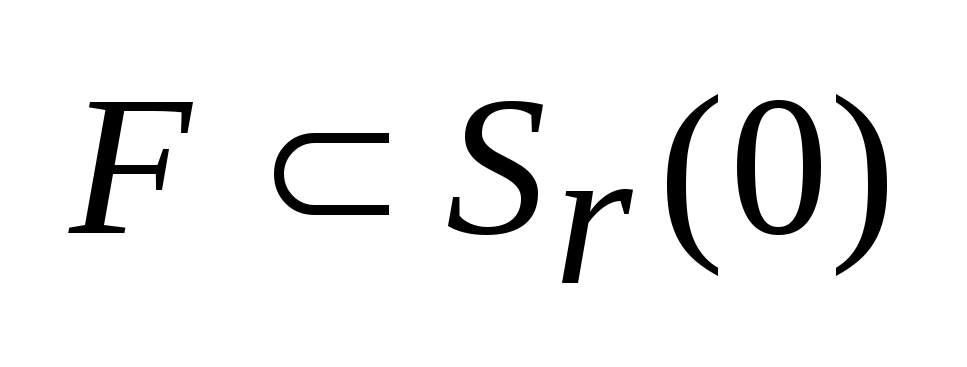 .
.
Хаусдорффова норма- это расстояние между мн-ми A и B:
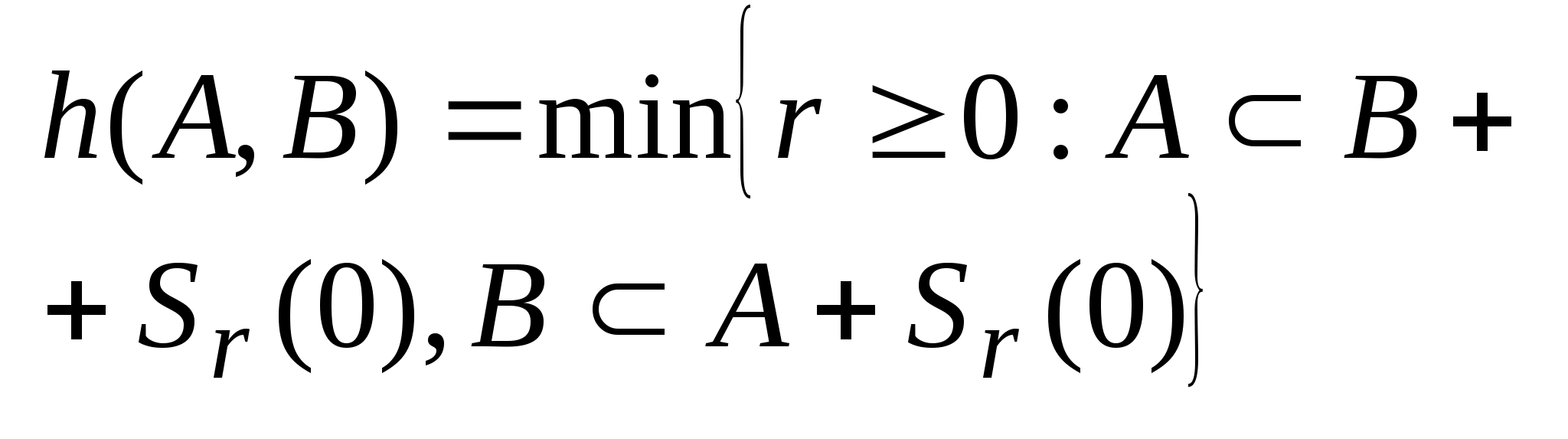 -расстояние
между мн-ми A
и B
(
-расстояние
между мн-ми A
и B
(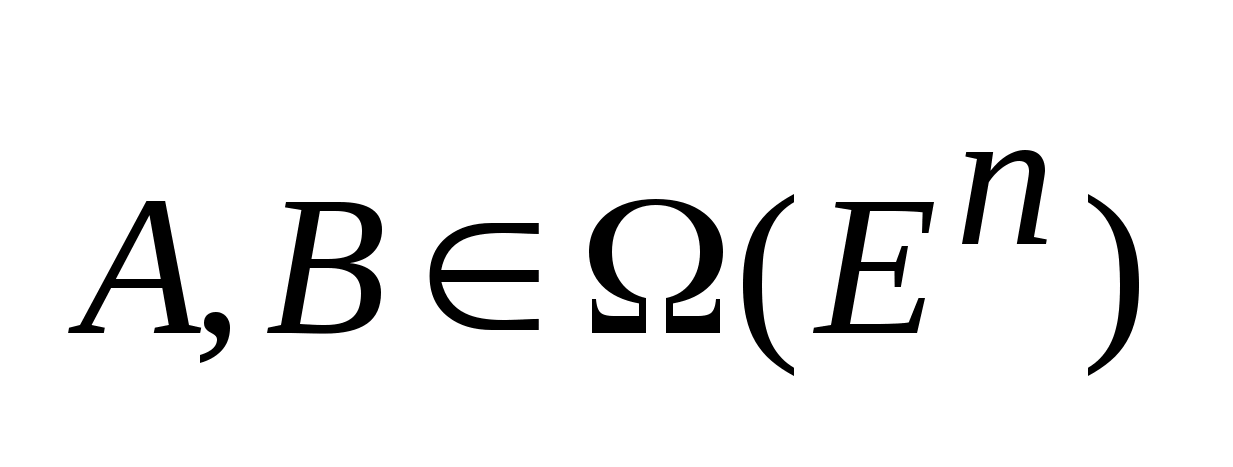 )
явл. наименьшее положительное число r.
)
явл. наименьшее положительное число r.
Лемма:
Пусть
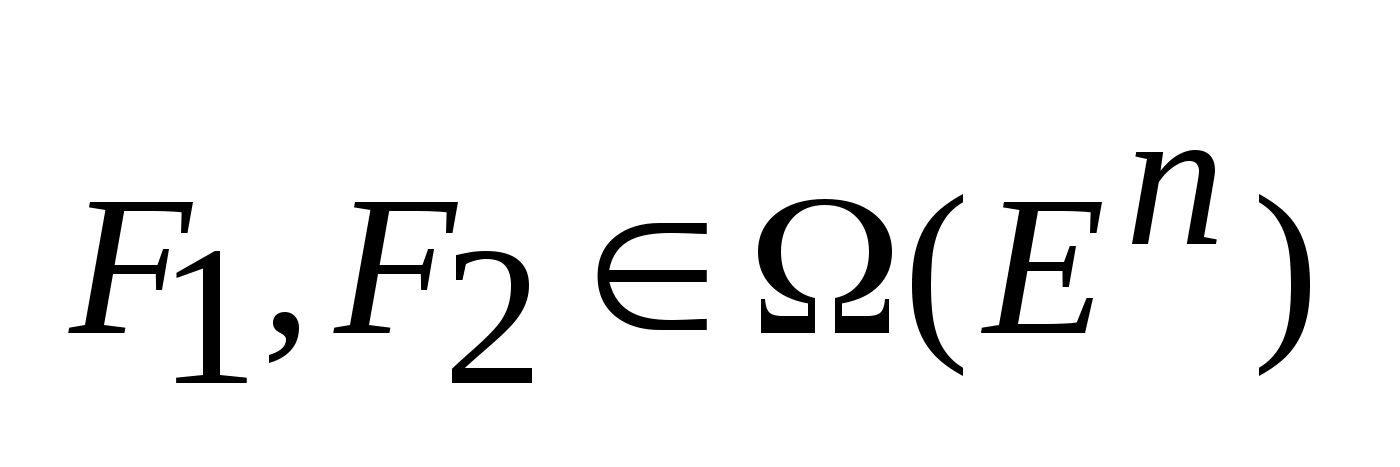 -
выпуклы, тогда хаусдорффова норма
-
выпуклы, тогда хаусдорффова норма
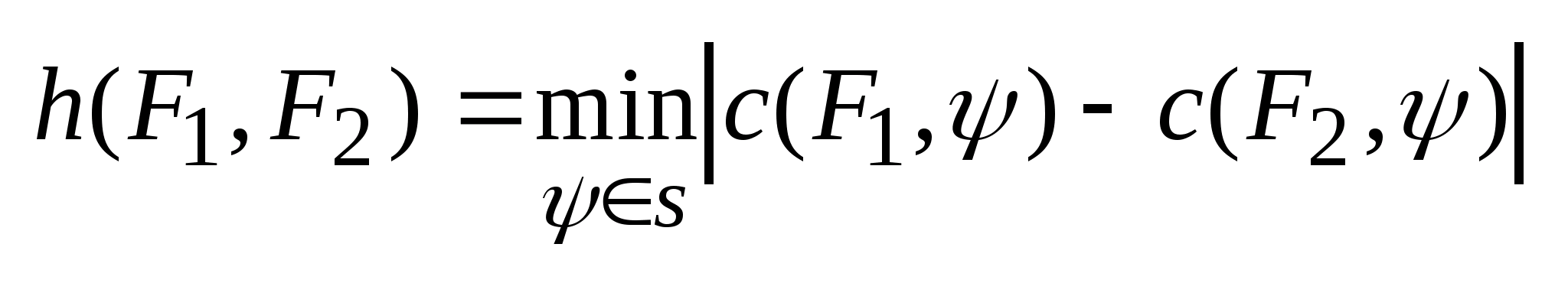
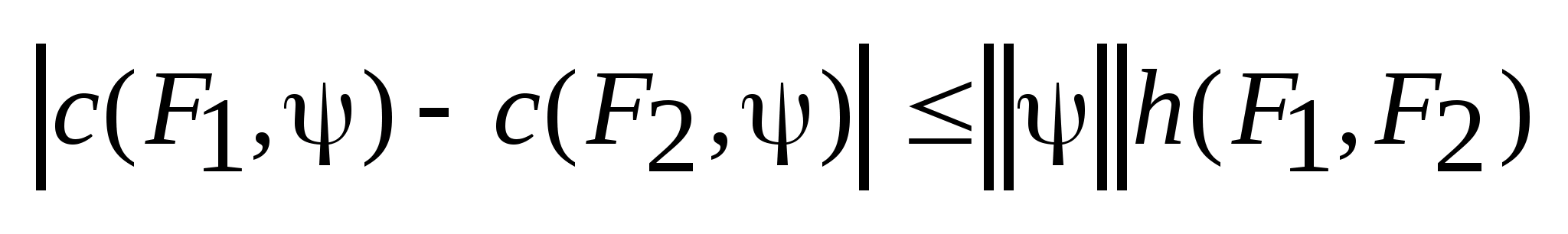
6. Опорные функции.
Задано
множество
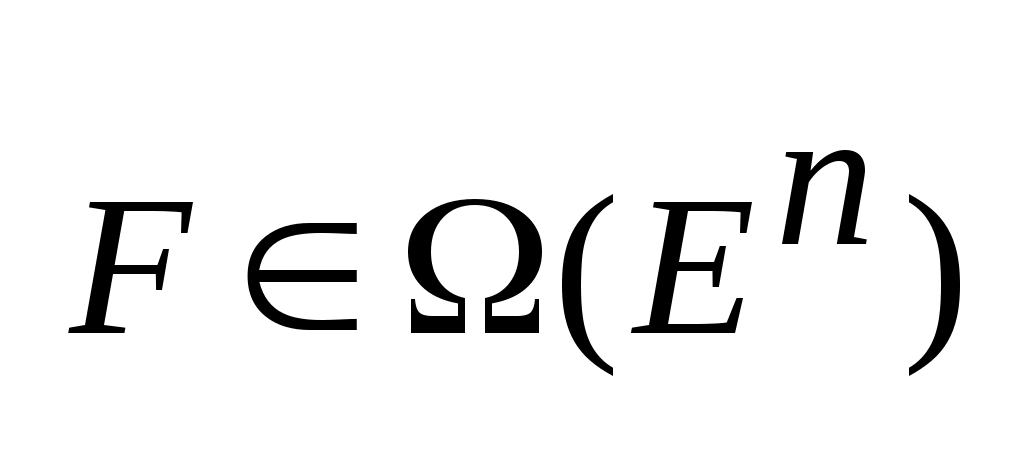 и
вектор
и
вектор
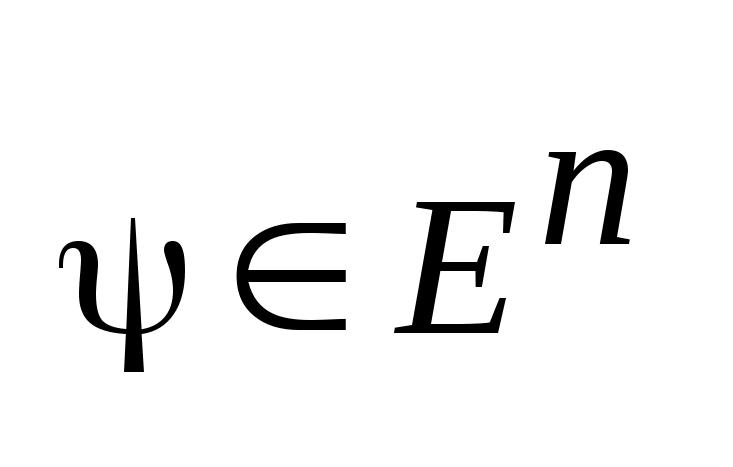 . Для этих двух элементов можно определить
опорную функцию следующим образом
. Для этих двух элементов можно определить
опорную функцию следующим образом
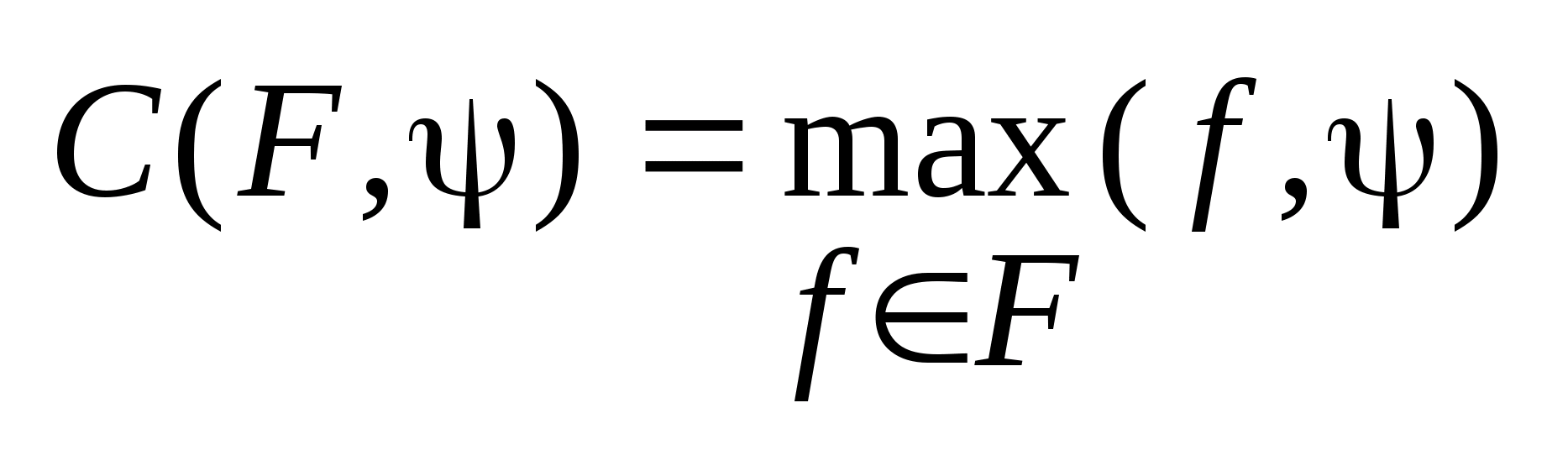 ,
где C
опорная функция.
,
где C
опорная функция.
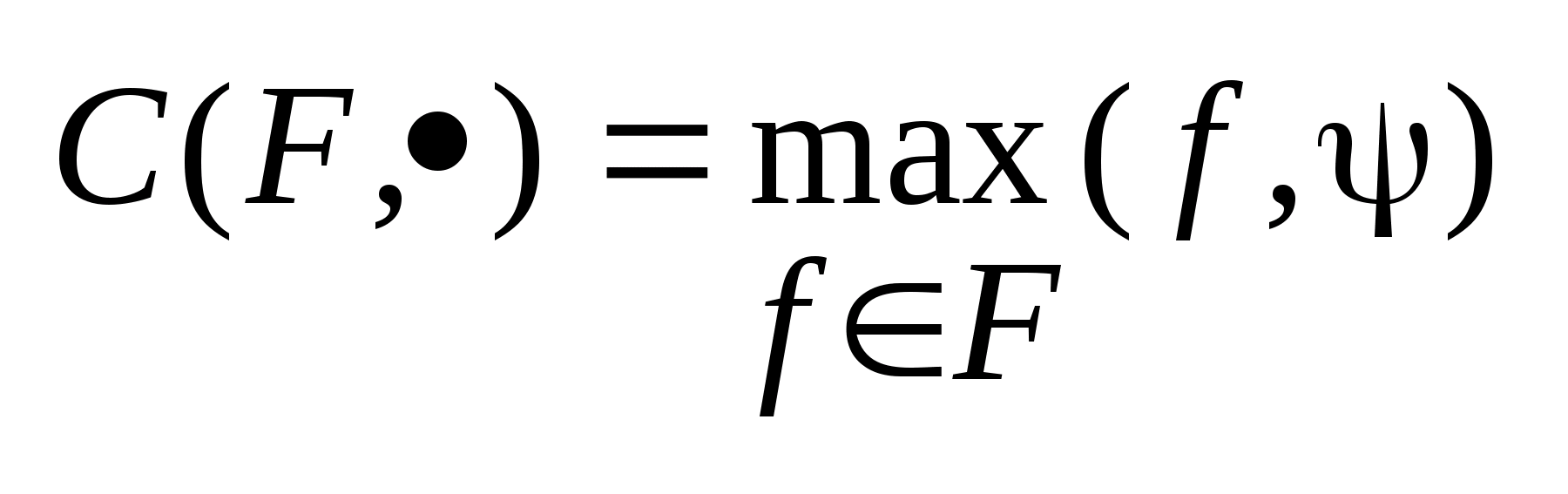 ,
,
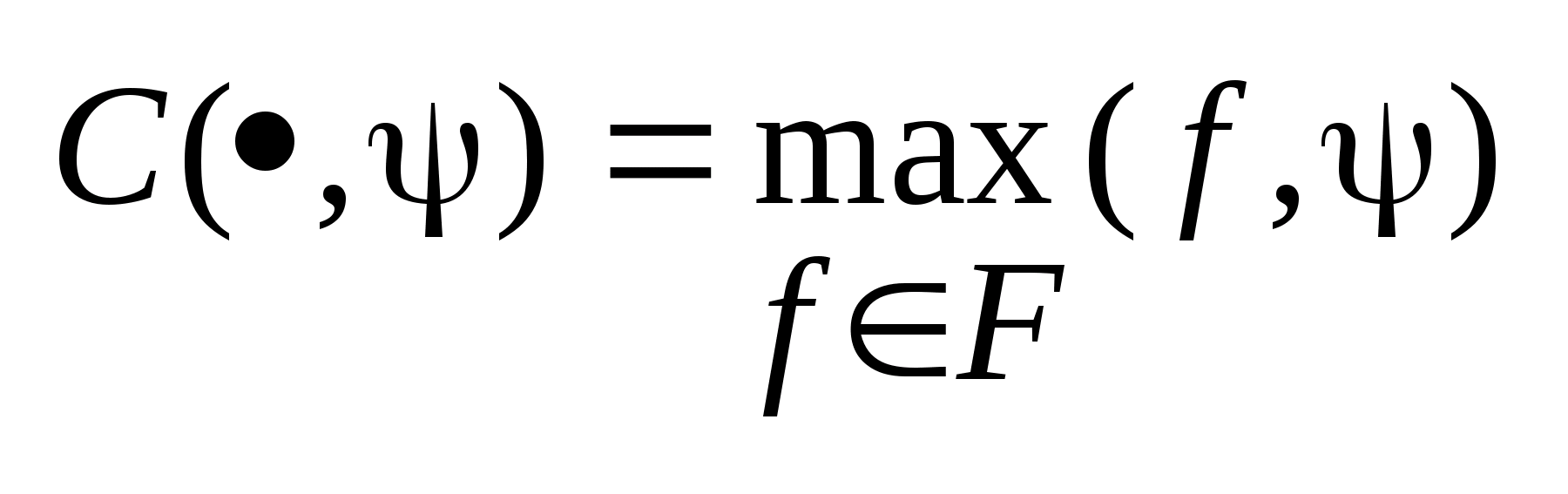
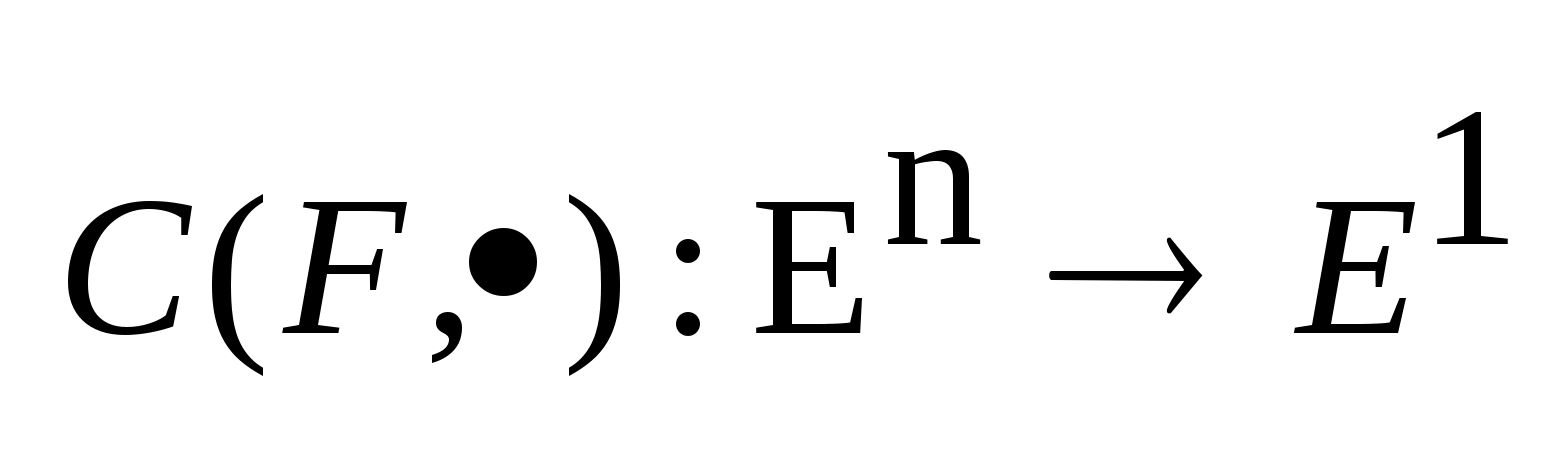 ,
,
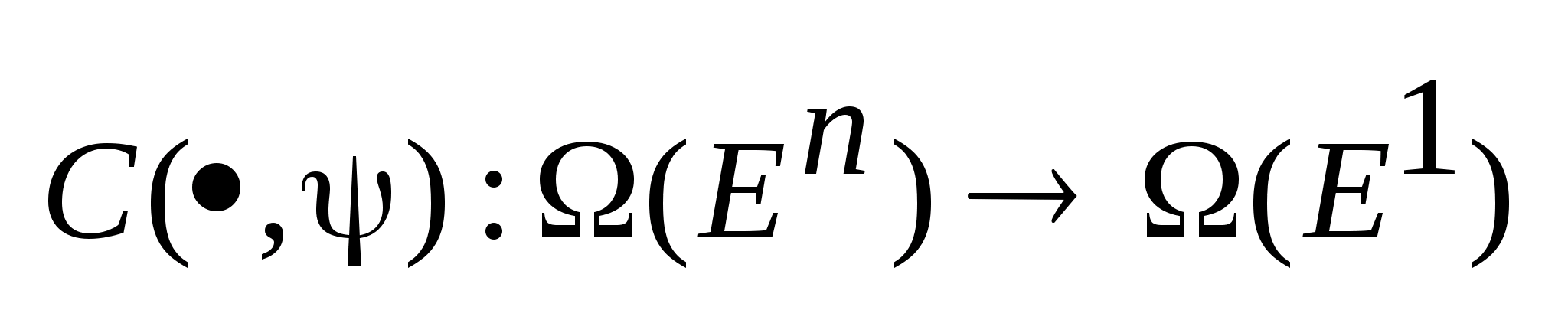 .
.
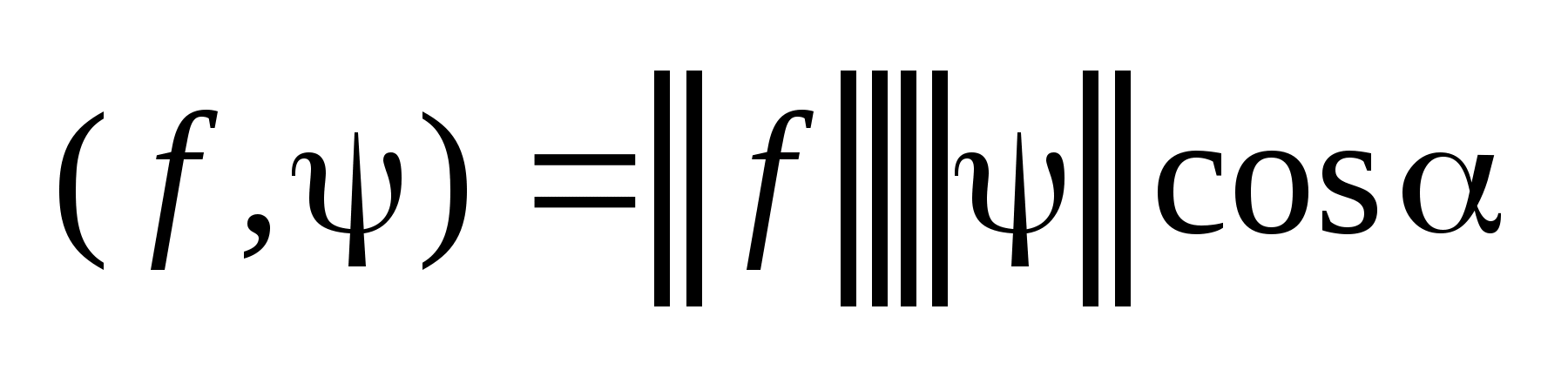 ,
,
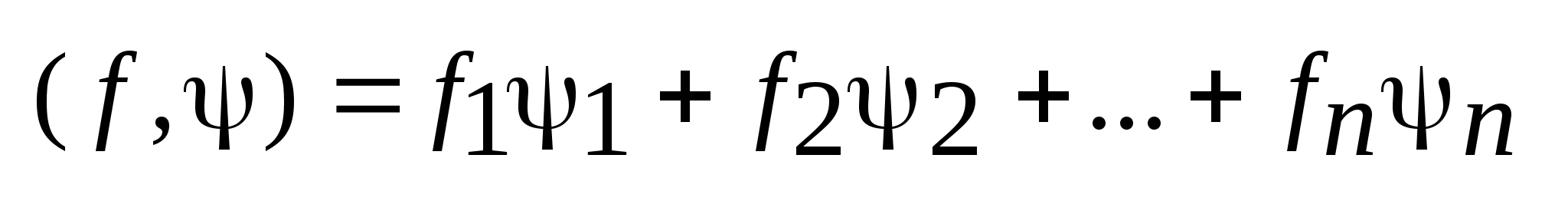
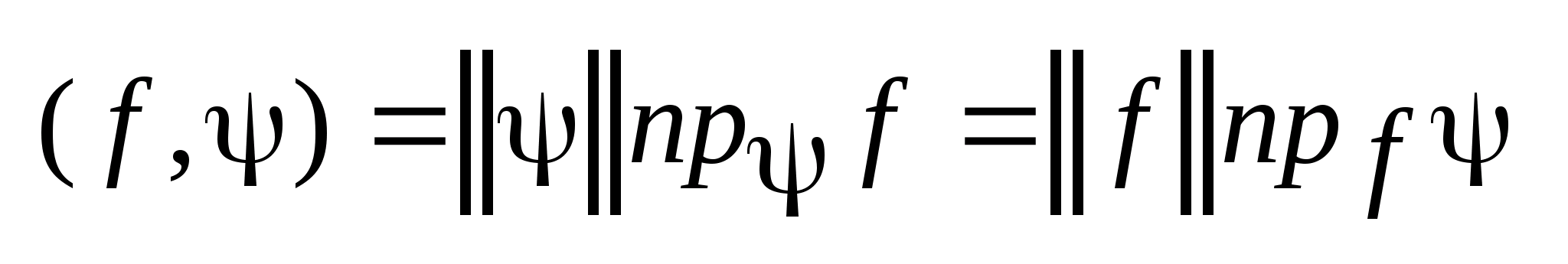 .
.
Пусть
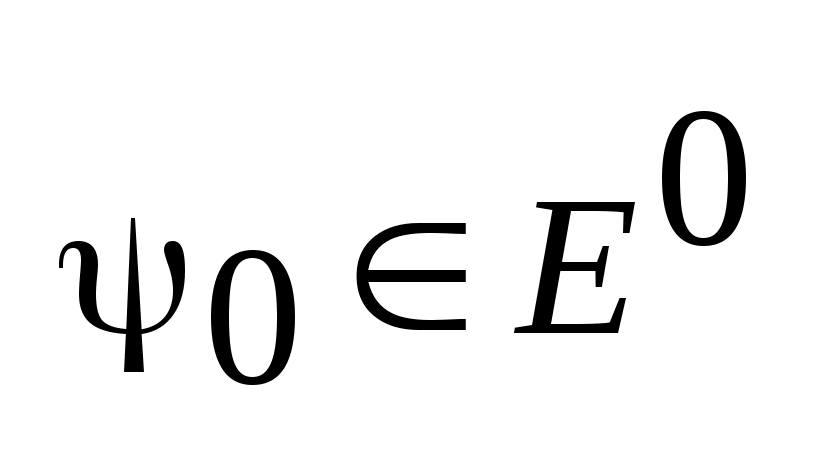 -некоторый
фиксированный вектор, а
-некоторый
фиксированный вектор, а
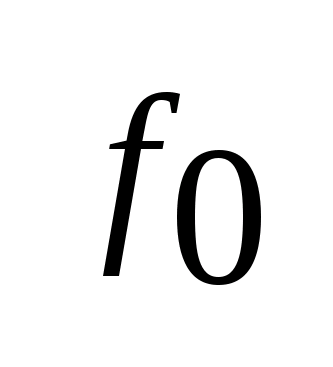 один
из векторов множества F,
на котором опорная функция достигает
максимум:
один
из векторов множества F,
на котором опорная функция достигает
максимум:
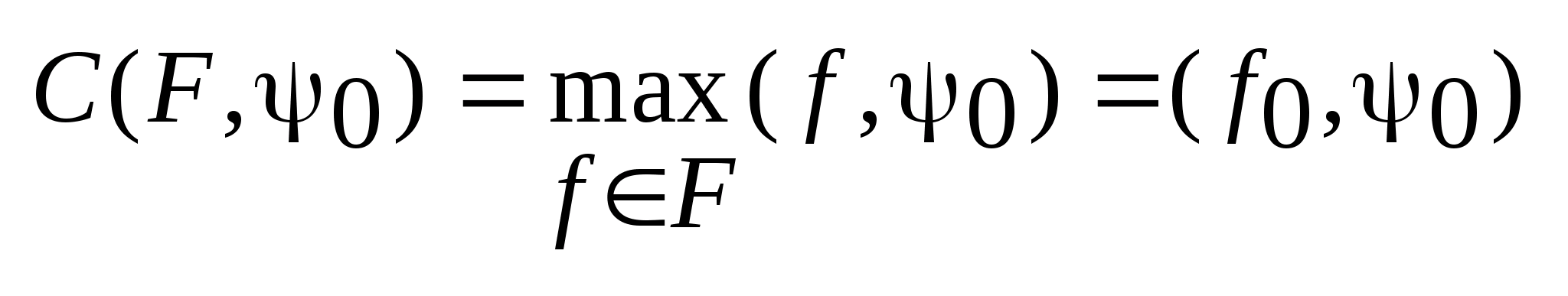 .
В этом случае
.
В этом случае
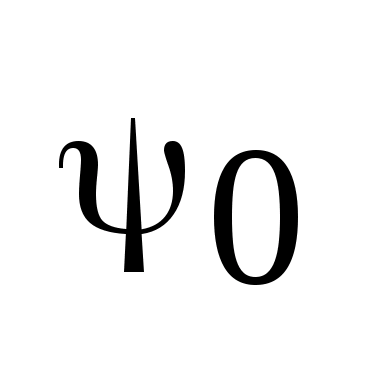 наз.
опорным вектором мн-ва F
в точке
наз.
опорным вектором мн-ва F
в точке
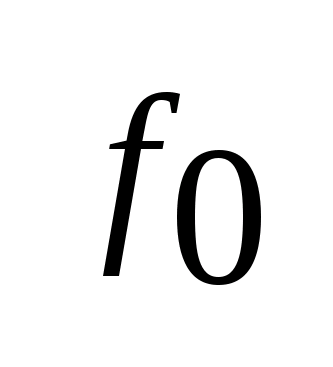 .
А совокупность всех векторов
.
А совокупность всех векторов
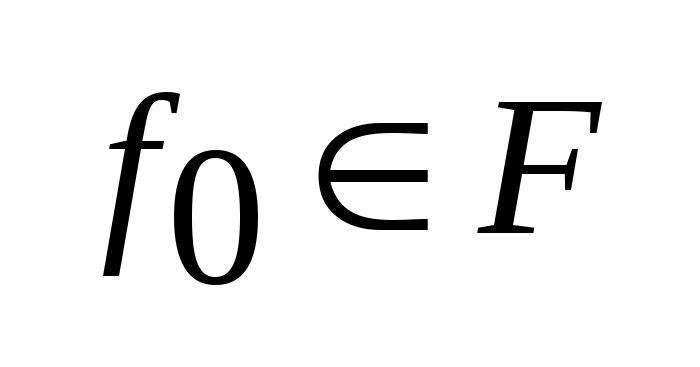 наз.
опорным множеством к множеству F
в
направлении
наз.
опорным множеством к множеству F
в
направлении
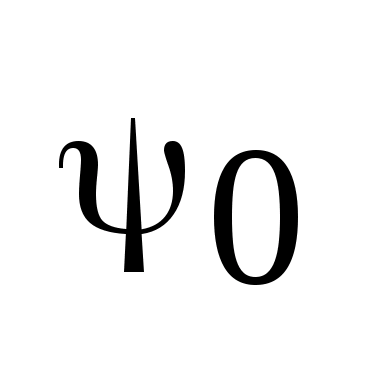 .Гиперплоскость
.Гиперплоскость
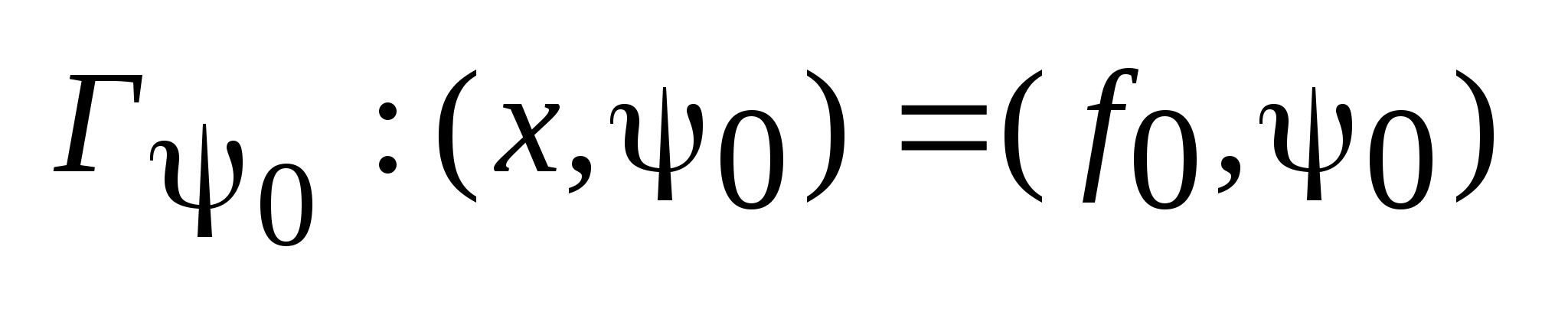 -
наз. опорной гиперплоскостью к множеству
F
в направлении
-
наз. опорной гиперплоскостью к множеству
F
в направлении
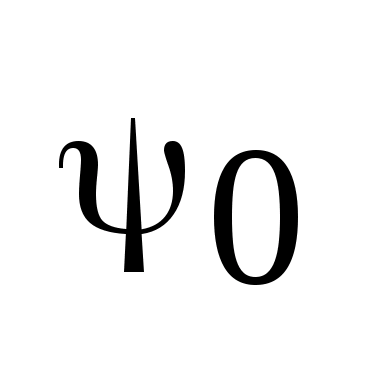 .
Гиперплоскость
.
Гиперплоскость
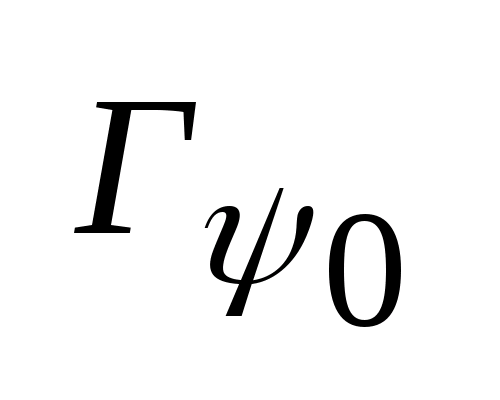 разбивает
разбивает
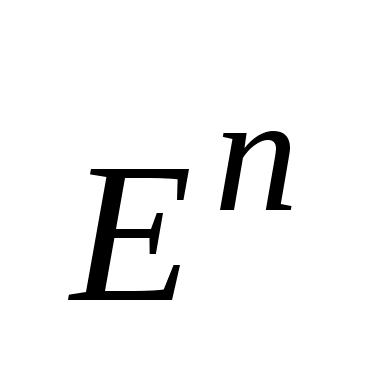 на
два подпространства, при этом множество
F
находится в отрезке получаемый
относительно
на
два подпространства, при этом множество
F
находится в отрезке получаемый
относительно
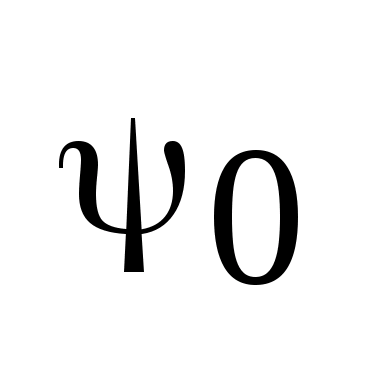 ,
т.к. для всех точек
,
т.к. для всех точек
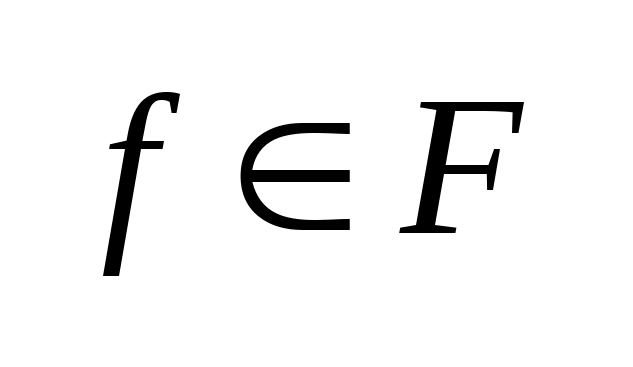 выполняется
неравенство
выполняется
неравенство
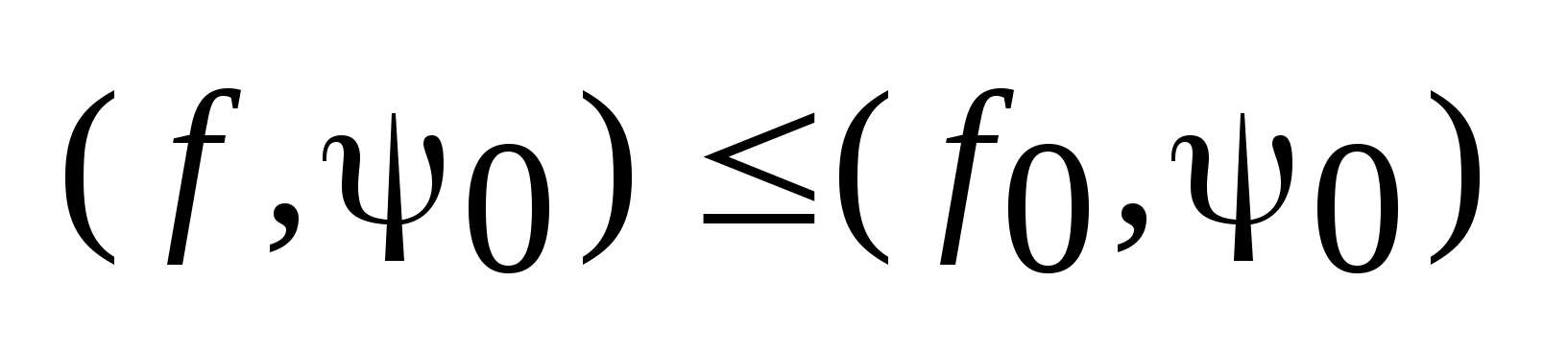 .
Если считать, что
.
Если считать, что
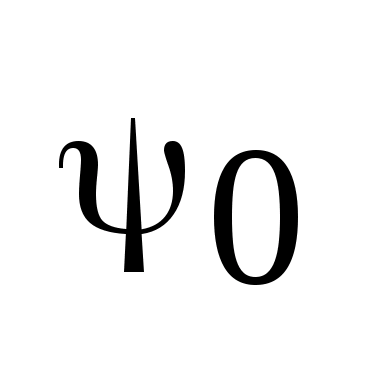 -
единичный вектор,
-
единичный вектор,
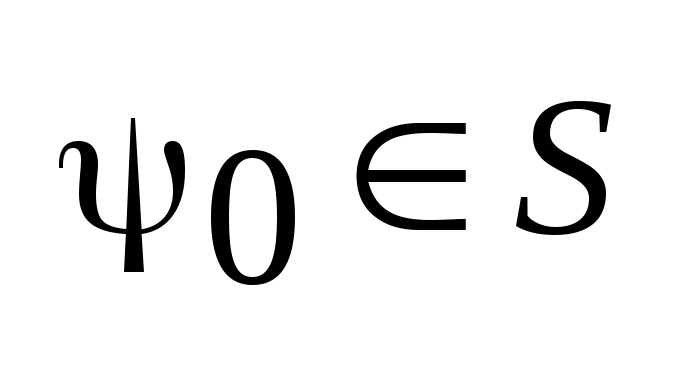 ,
,
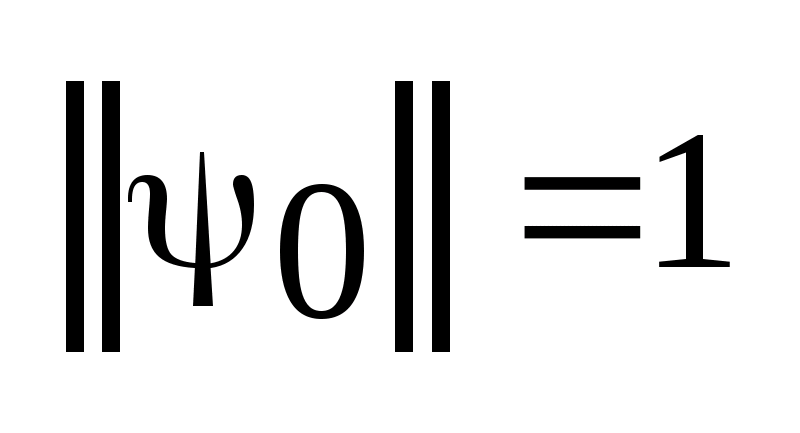 .
опорных
.
опорных
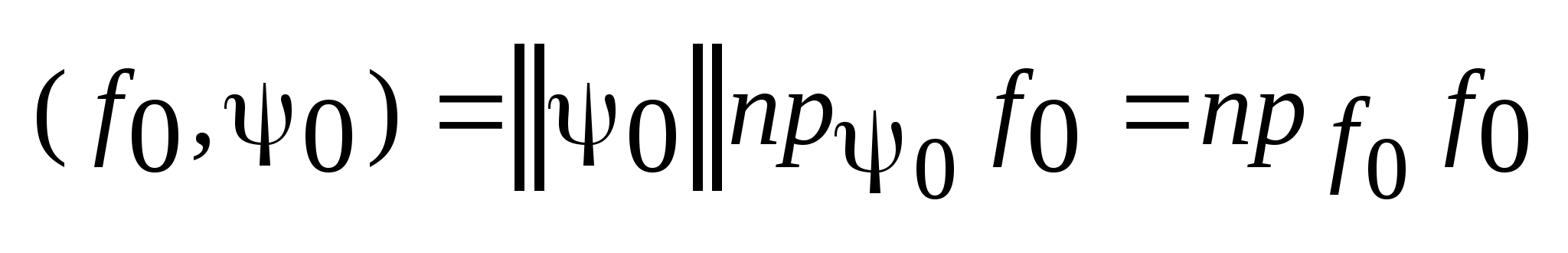
7. Свойства опорной функции.
1.
Опорные
функция- положительно однородная по
переменной
 .
.
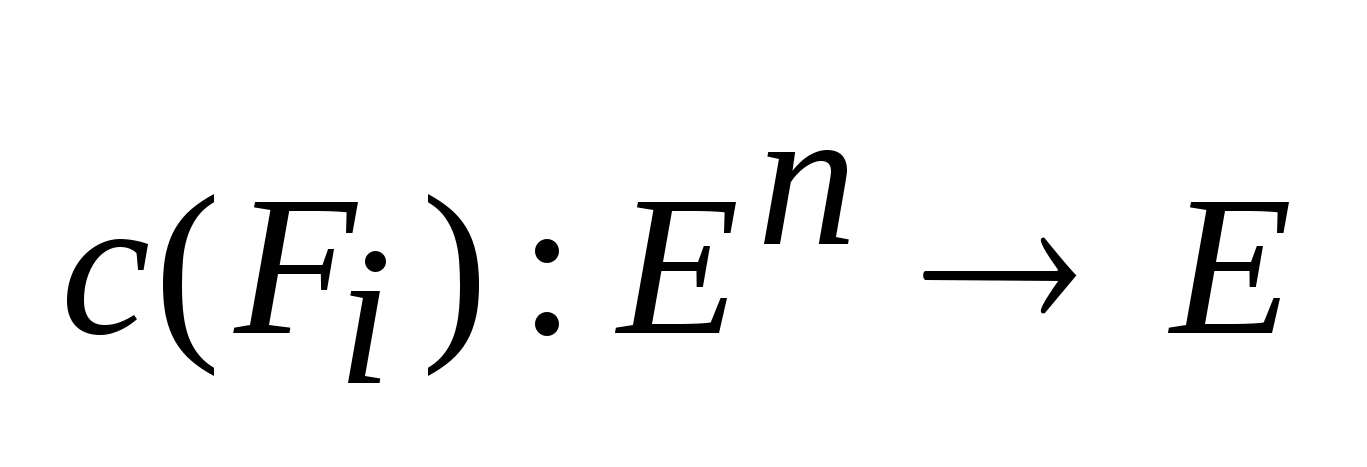 .
Это значит что
.
Это значит что
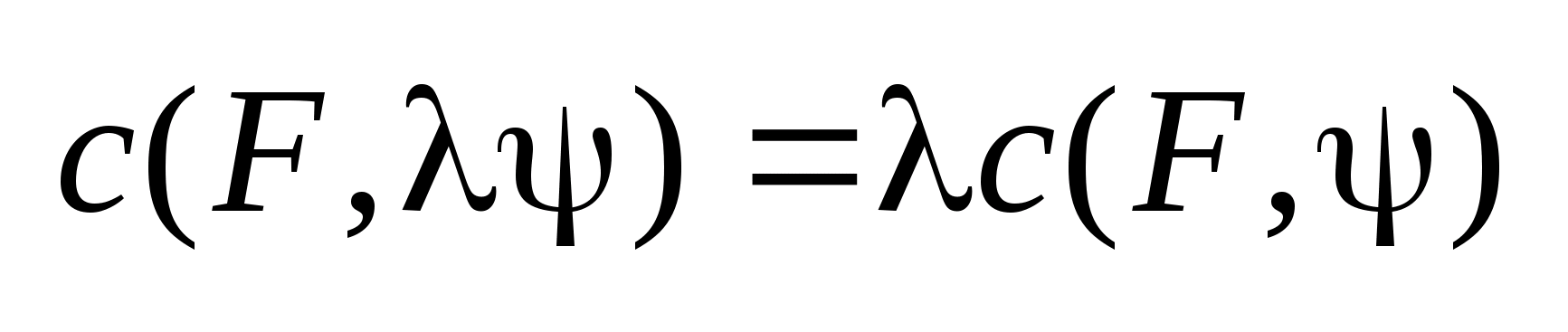
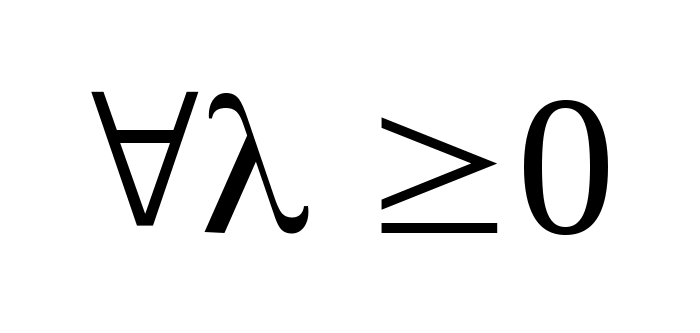 ,
,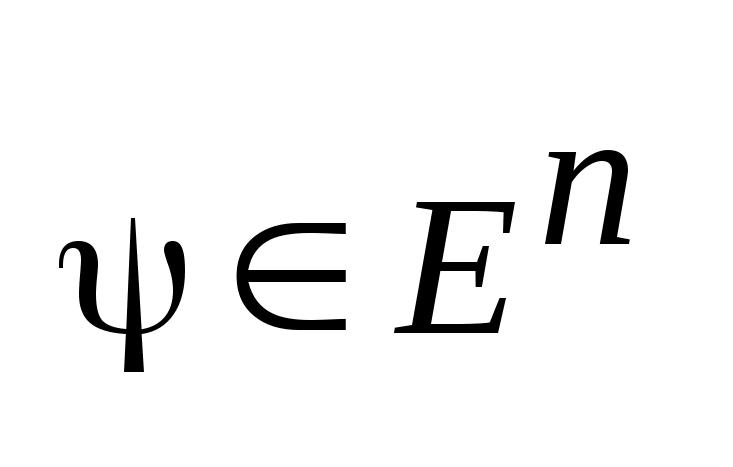 .
.
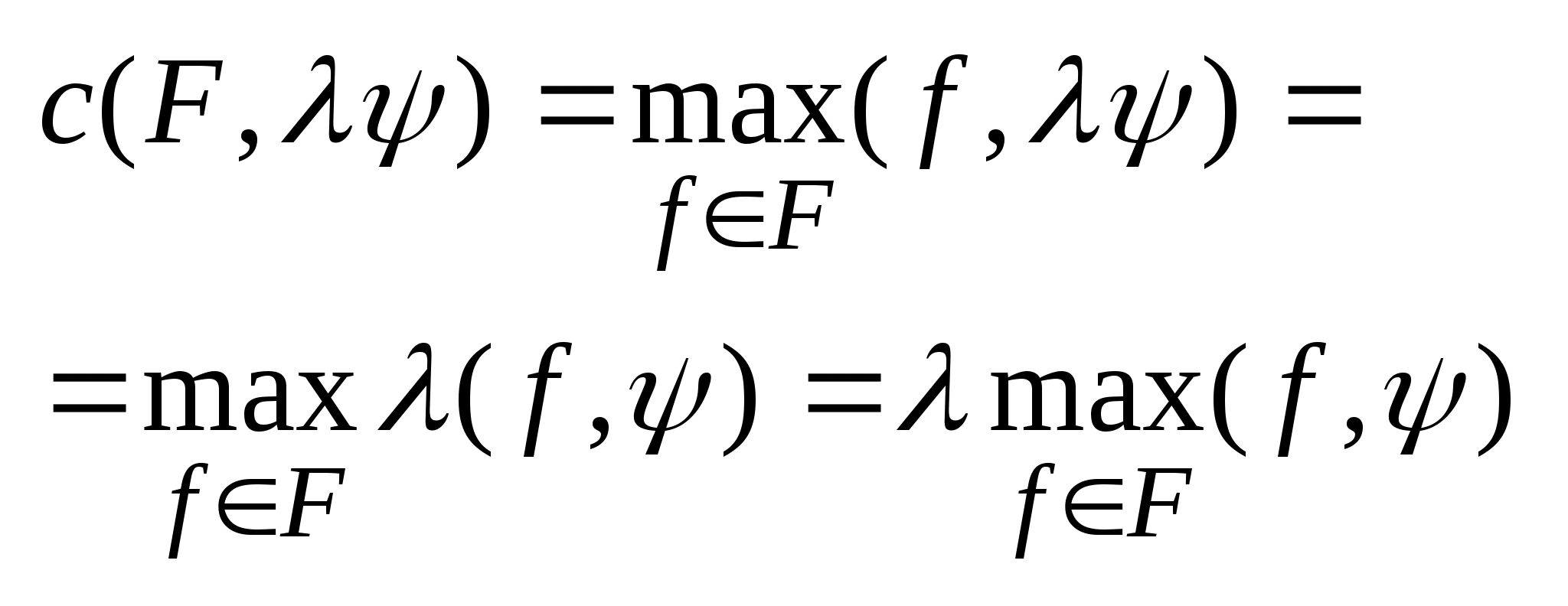
2.
Для
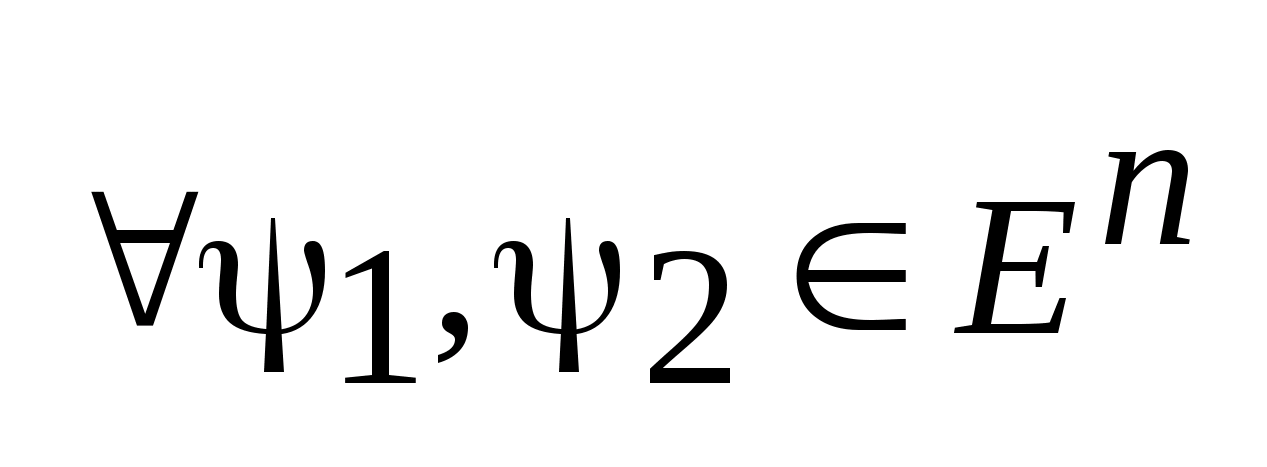 опорные
функции удовлетворяют неравенству:
опорные
функции удовлетворяют неравенству:
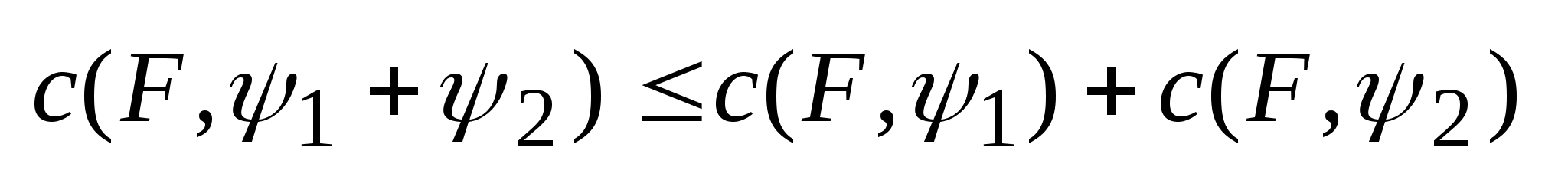 3.
Два
множества
3.
Два
множества
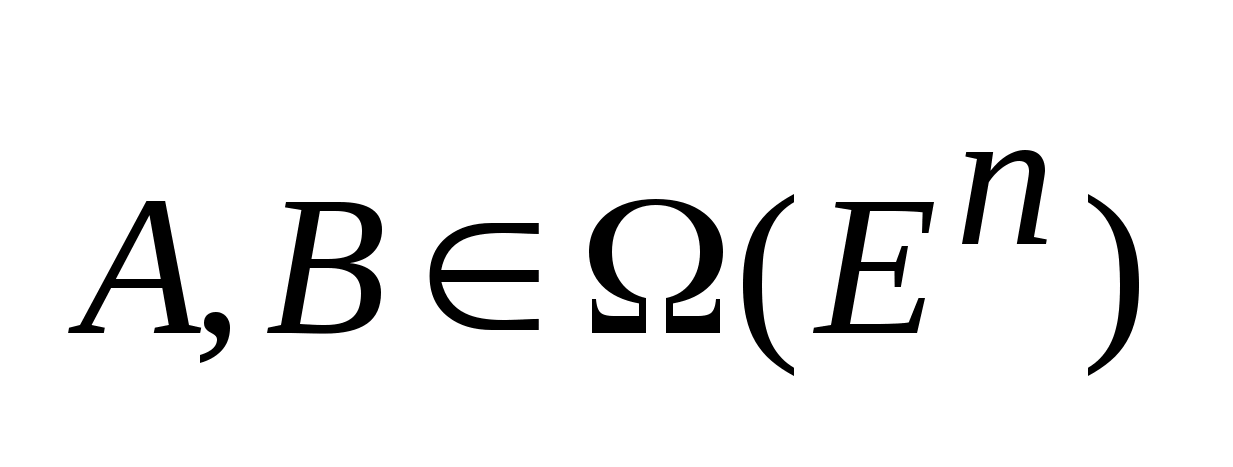 и
и
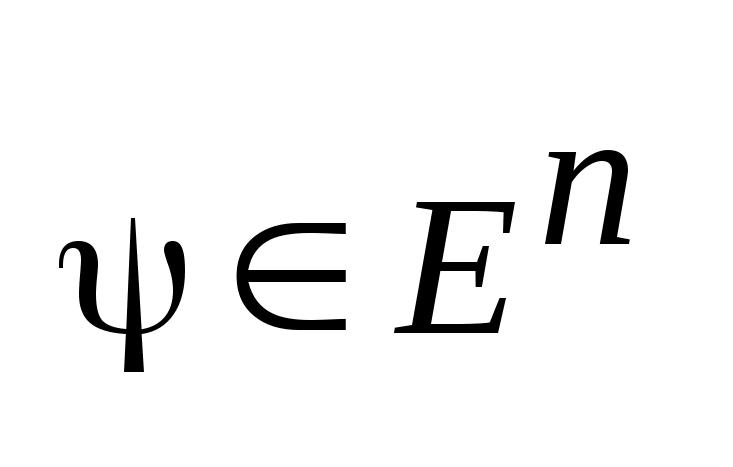 ,
,
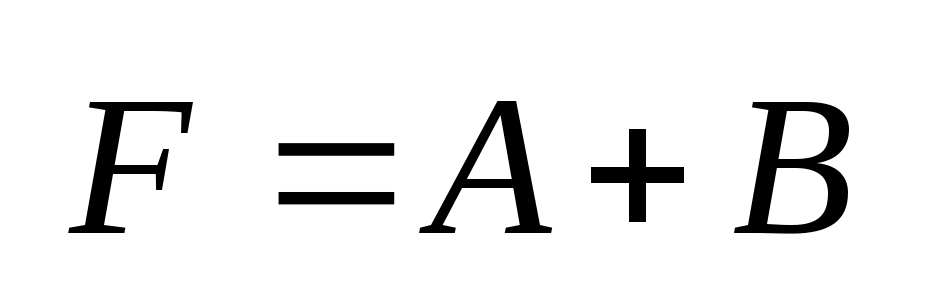 ,
,
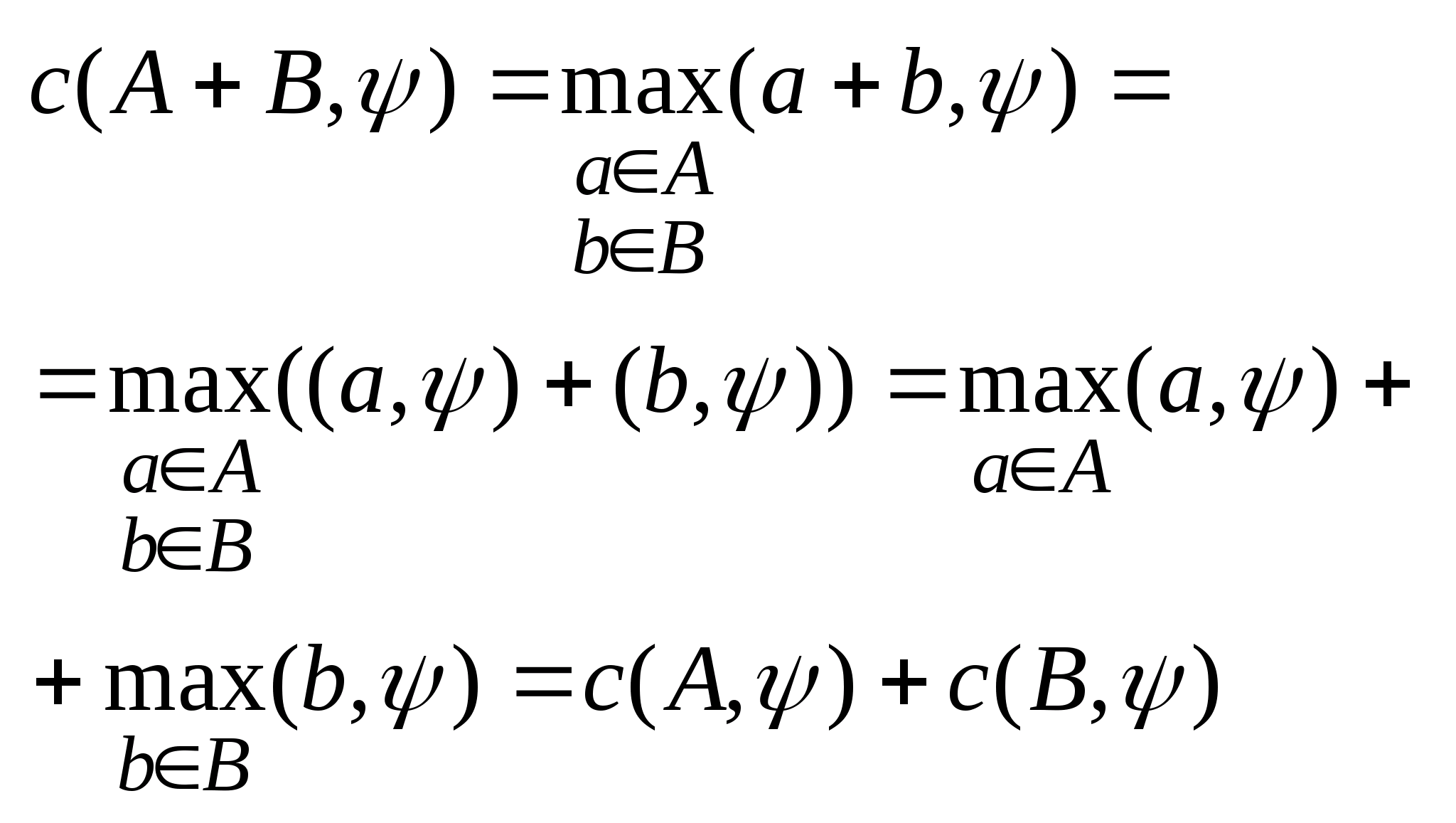 Пусть
матрица A
размера n
на
n,
Пусть
матрица A
размера n
на
n,
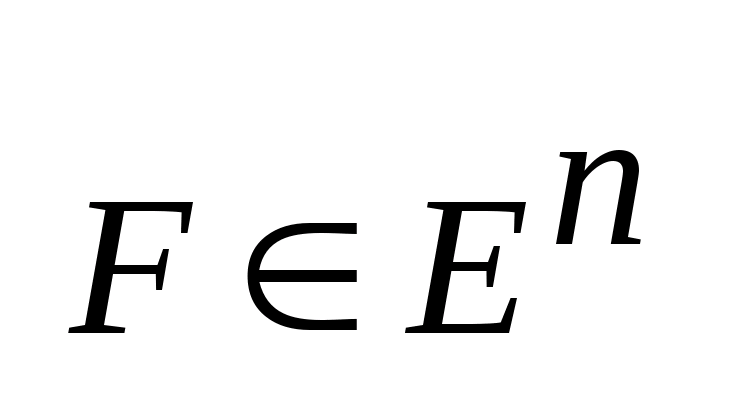 и
рассмотрим лин. образ множества F
при лин. преобразовании A
и
наз.
и
рассмотрим лин. образ множества F
при лин. преобразовании A
и
наз.
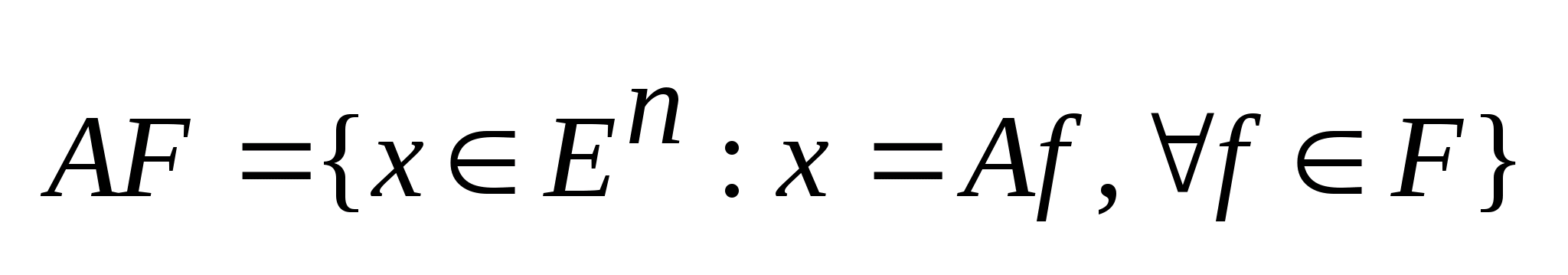 .
.
4.
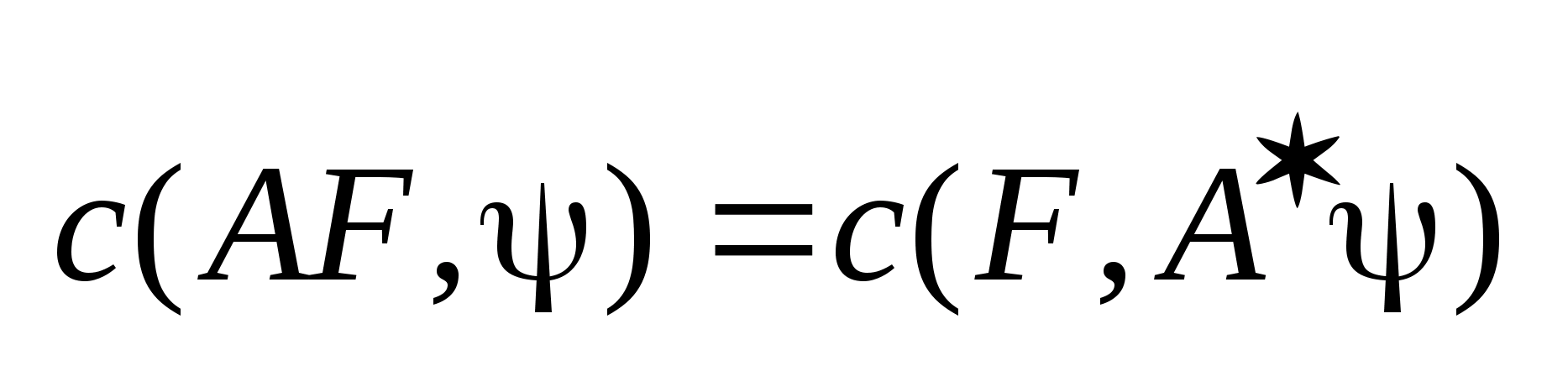 ,где
,где
 -матр.
сопряженная с матр.
-матр.
сопряженная с матр.
 .
.
5.
Опорная
функция положительная и однородная по
первому аргументу.
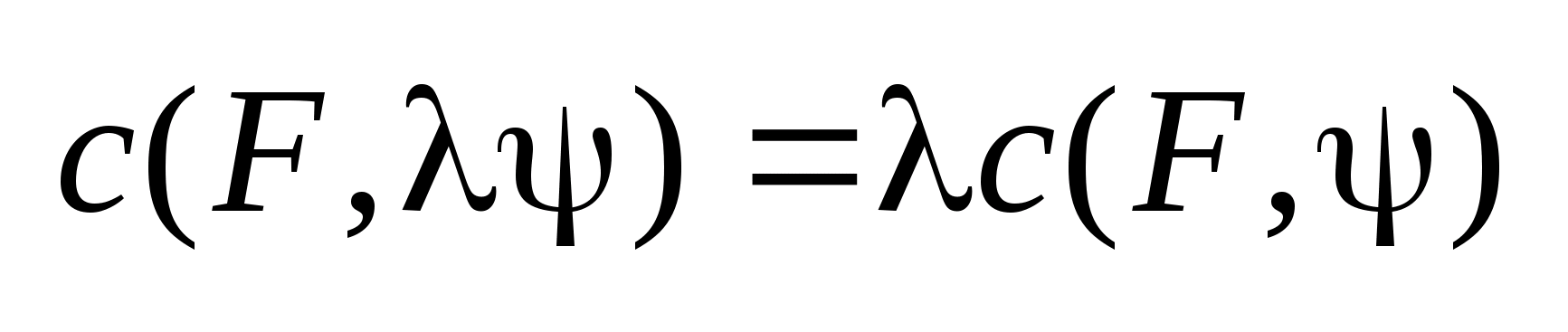 ,
,
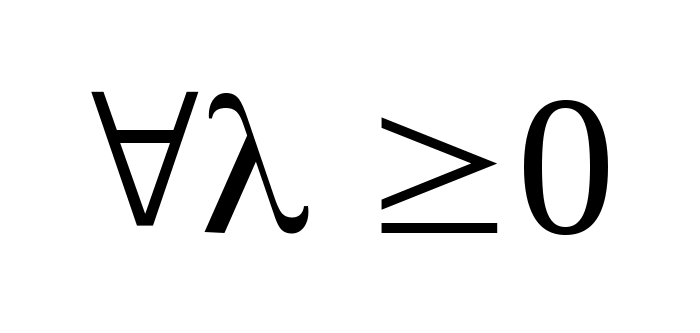 .
Пусть
.
Пусть
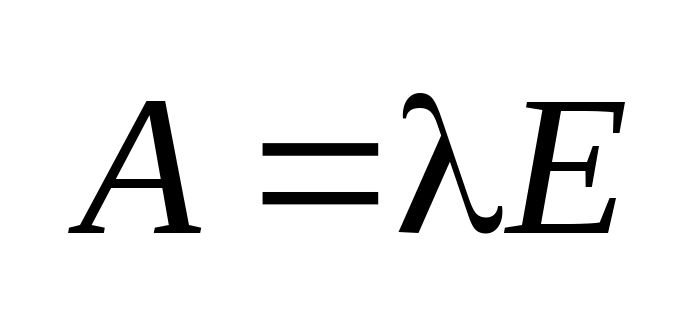 и пользуемся : 1) условием однородности:
и пользуемся : 1) условием однородности:
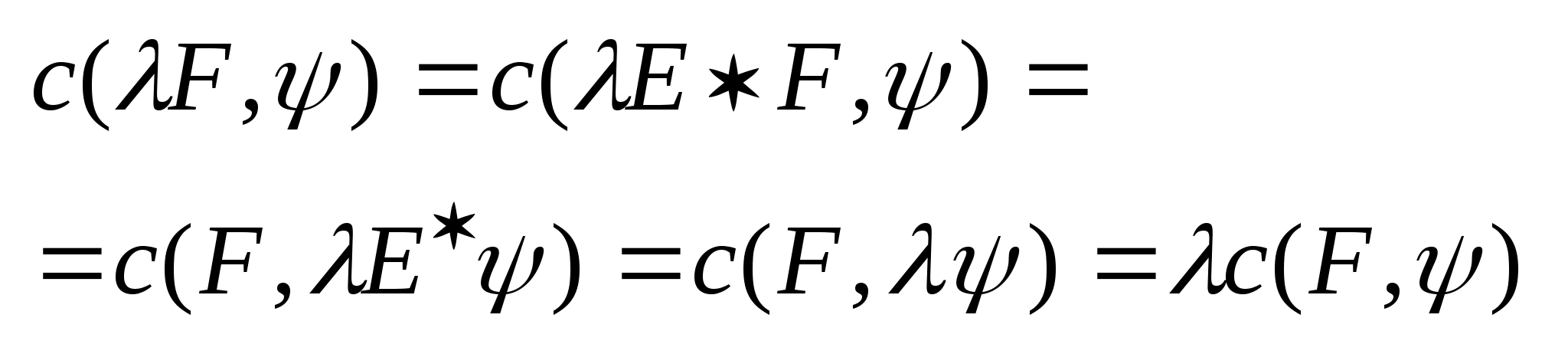 6.
Пусть
задано множество
6.
Пусть
задано множество
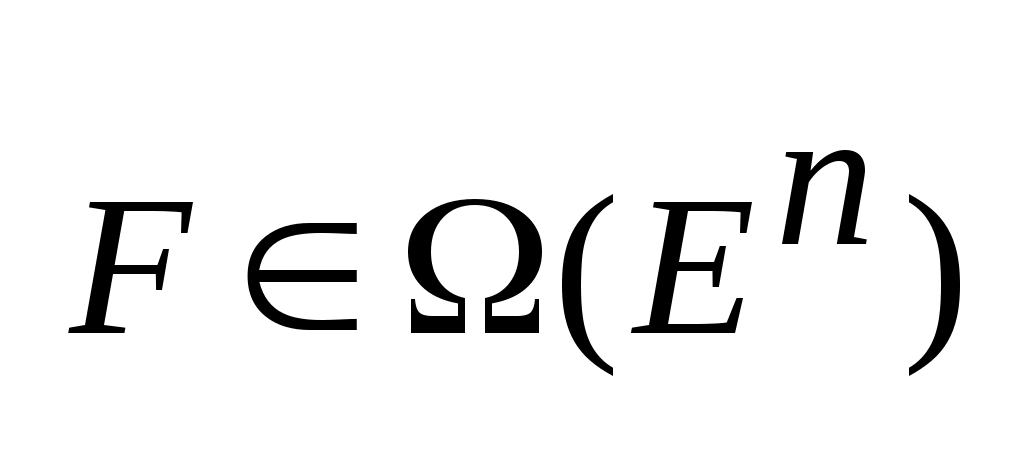 и
его опорная фун.
и
его опорная фун.
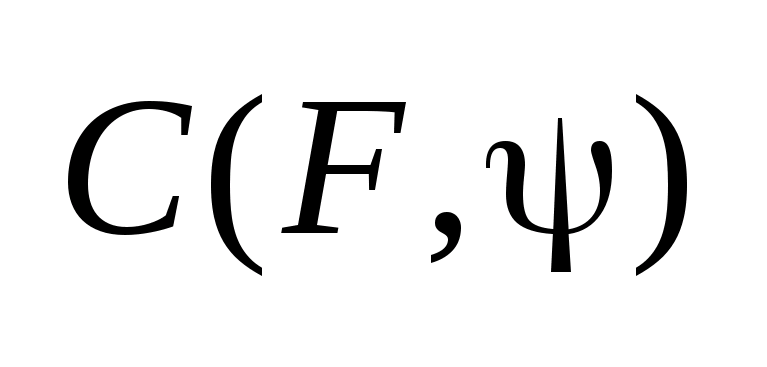 . Выпуклая оболочка мн-ва F
. Выпуклая оболочка мн-ва F
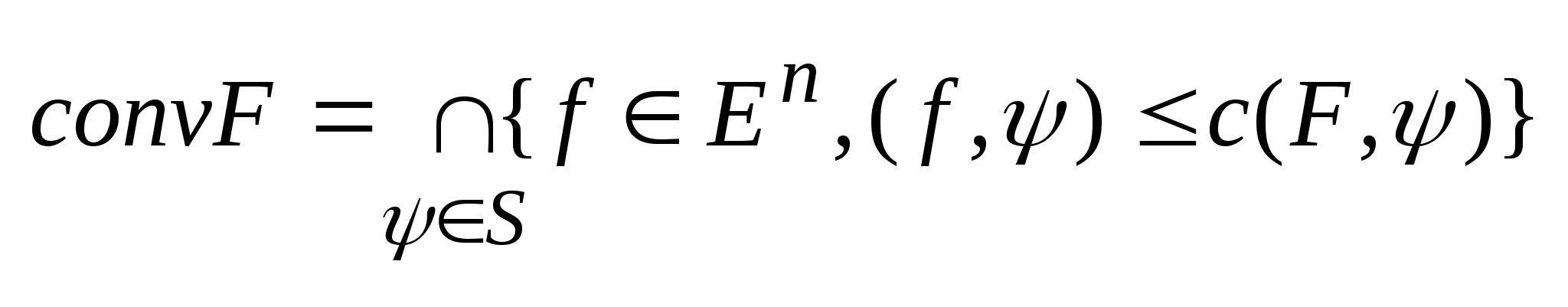 ,
,
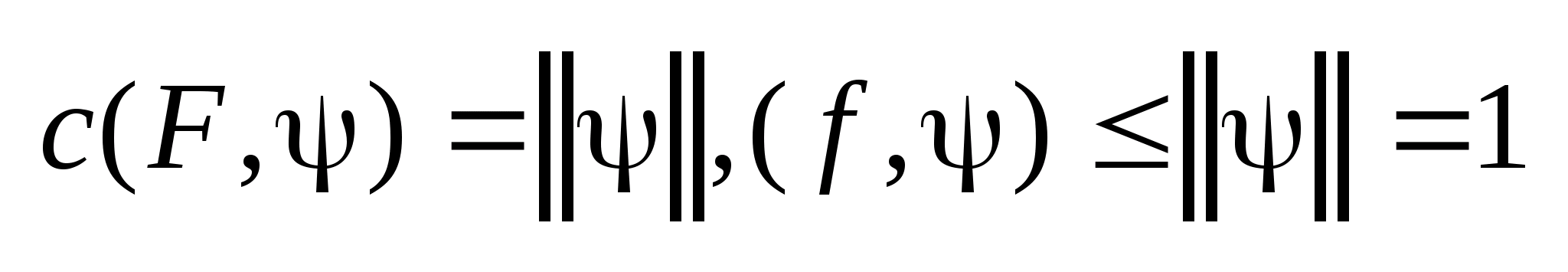 .
.
7.
Если
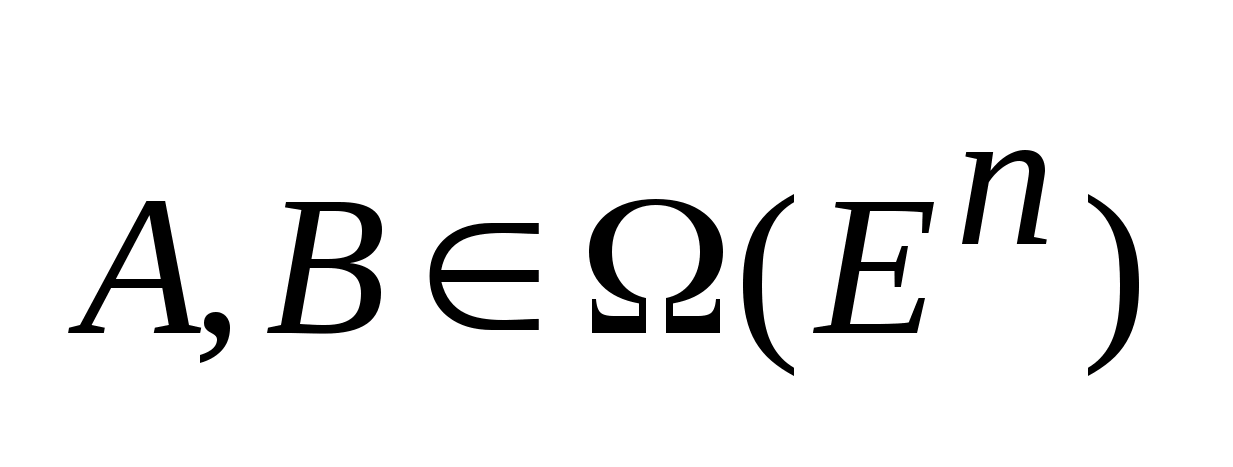 и
A=B,
то опорная фун.
и
A=B,
то опорная фун.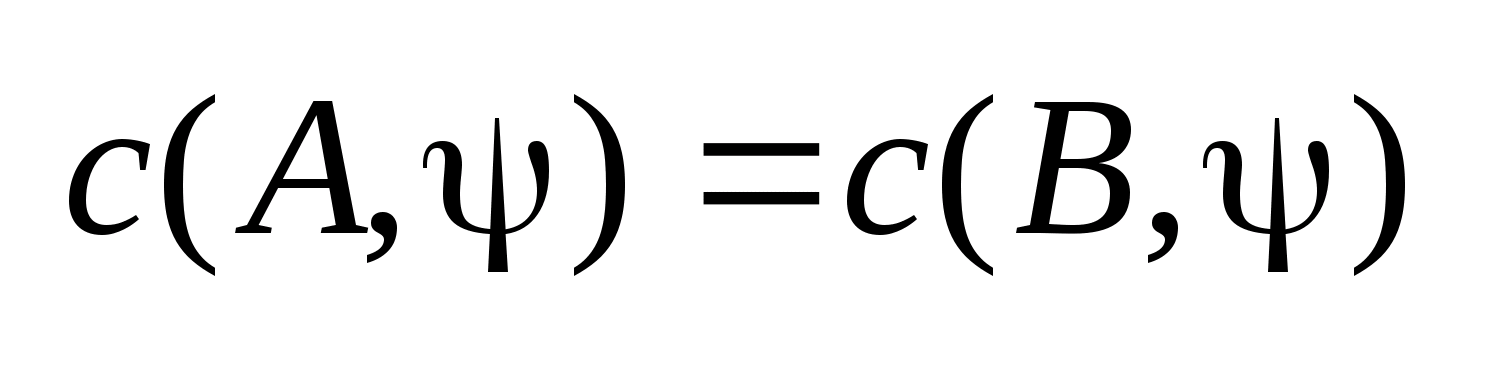 .
И наоборот, если
.
И наоборот, если
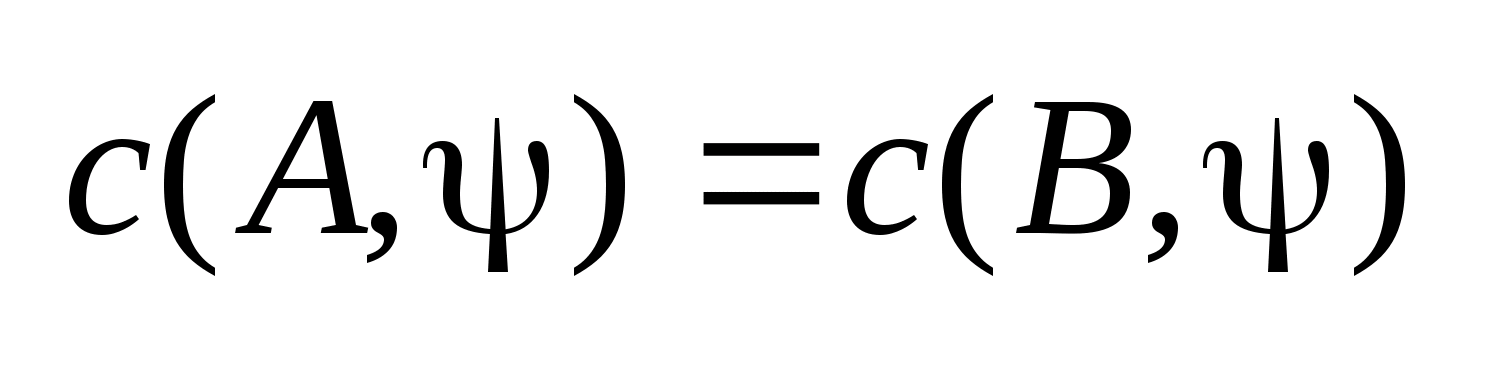 ,то
,то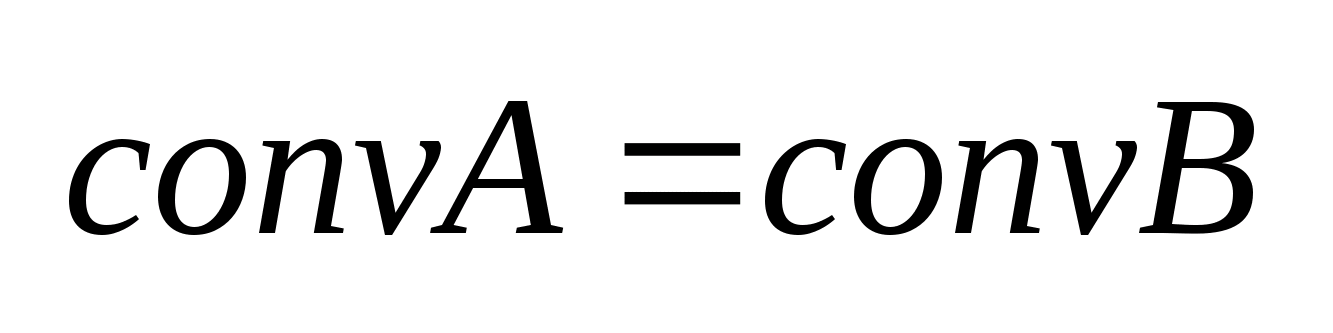 .
Следствие: Выпуклые мн-ва равны тогда
и только тогда, когда равны их опорные
функции.
.
Следствие: Выпуклые мн-ва равны тогда
и только тогда, когда равны их опорные
функции.
8.
Если
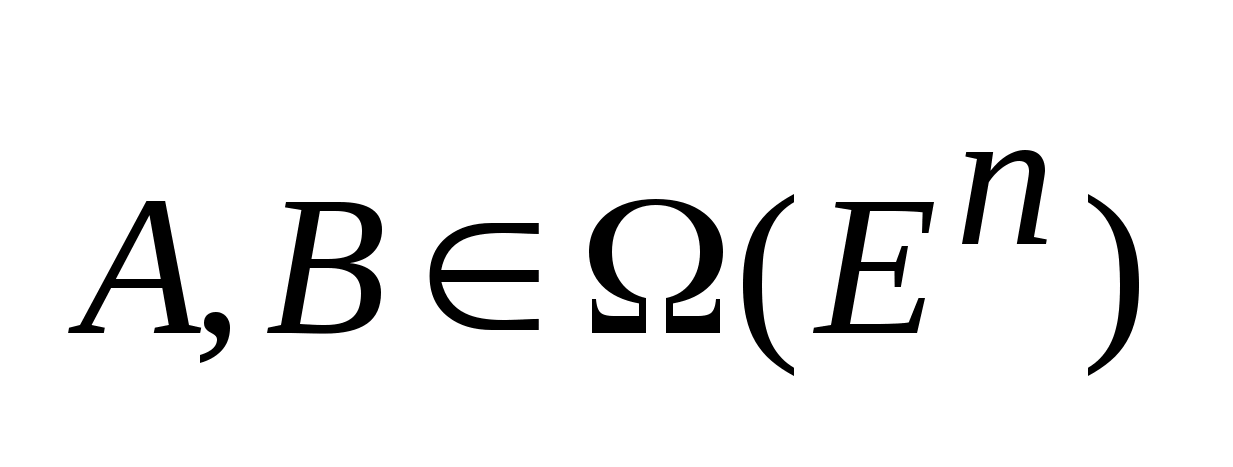 и
и
 .
В этом случае
.
В этом случае
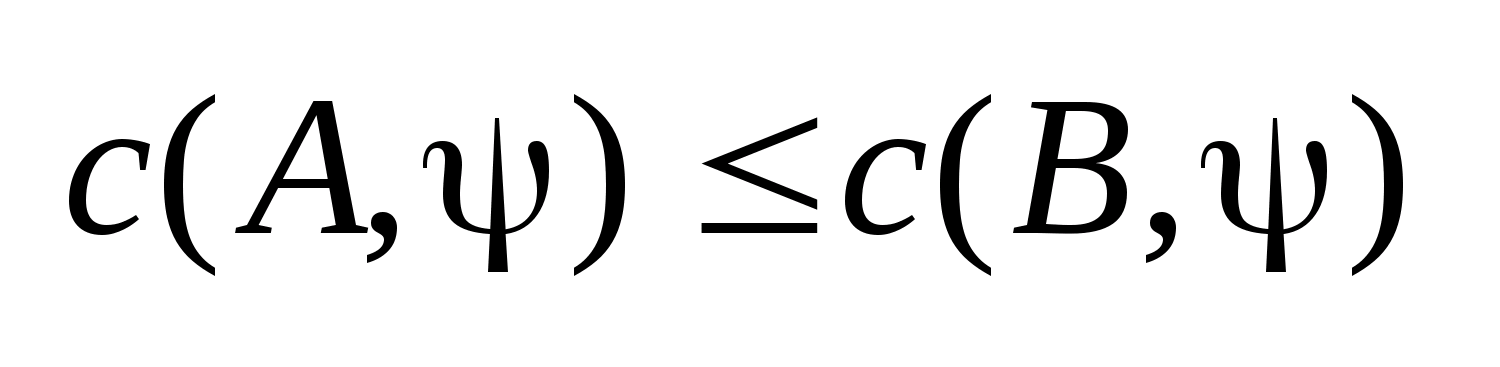 .
Если
.
Если
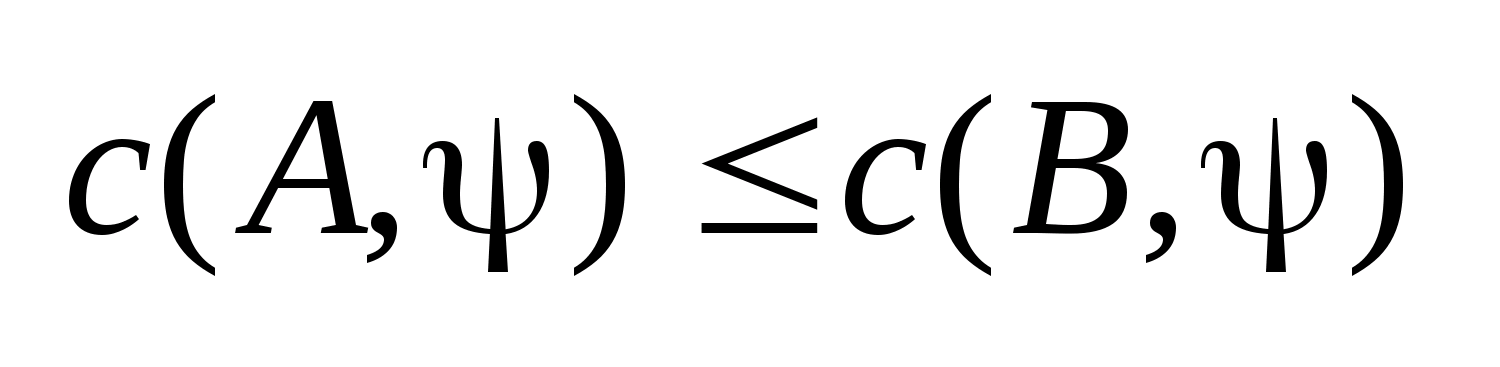 ,то
,то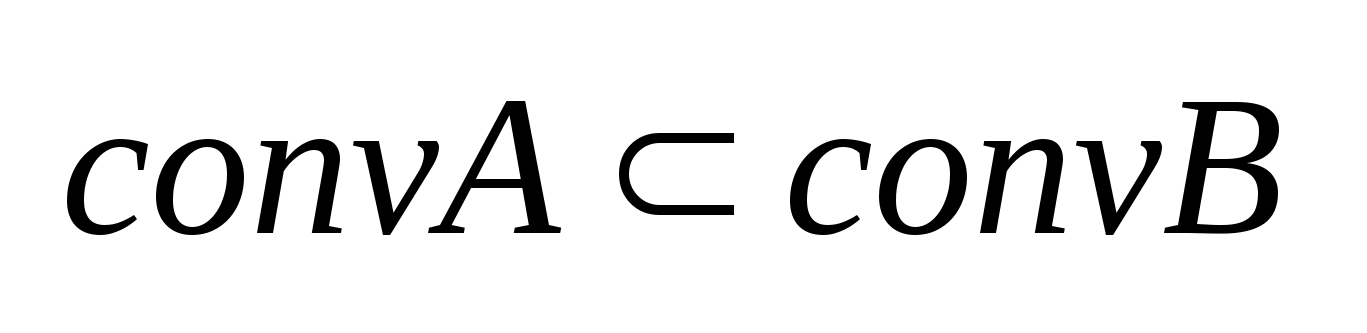 .
Следствие: Выпуклые мн-ва
.
Следствие: Выпуклые мн-ва
 тогда и только тогда, когда равны их
опорные функции
тогда и только тогда, когда равны их
опорные функции
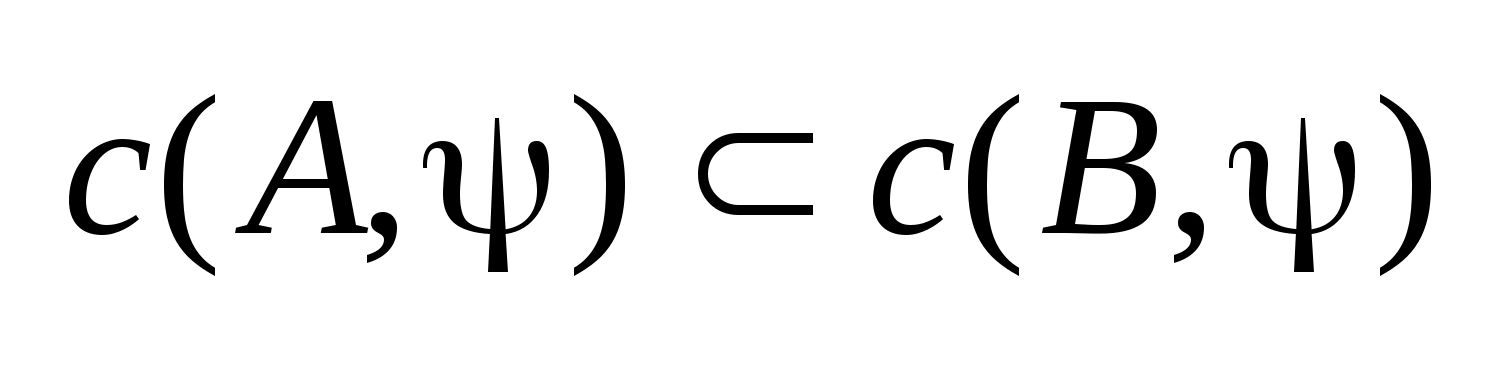 .
.
9.
Пусть
задано множество
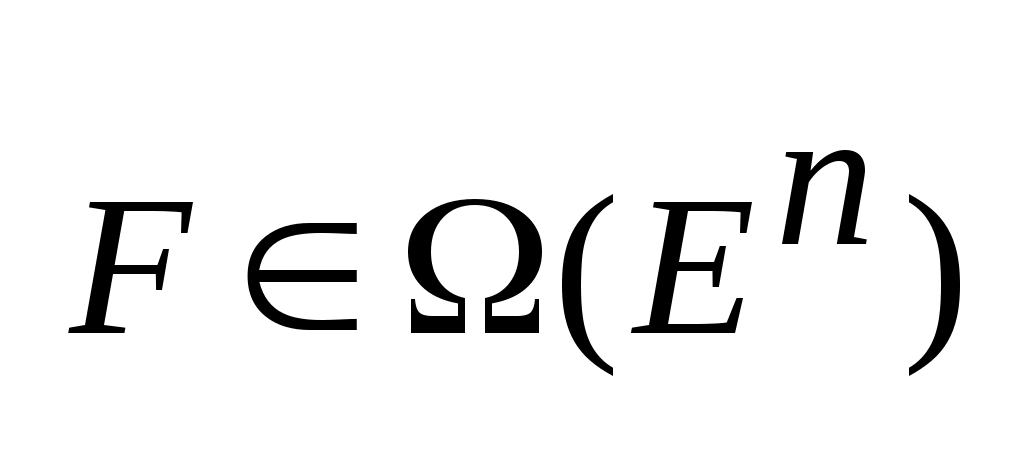 ,
тогда
,
тогда
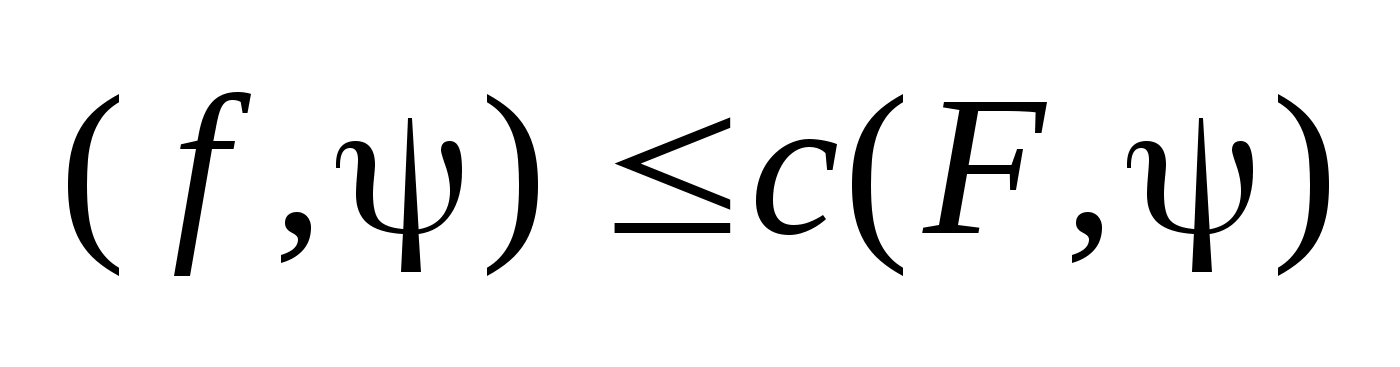 .
В обратную сторону:
.
В обратную сторону:
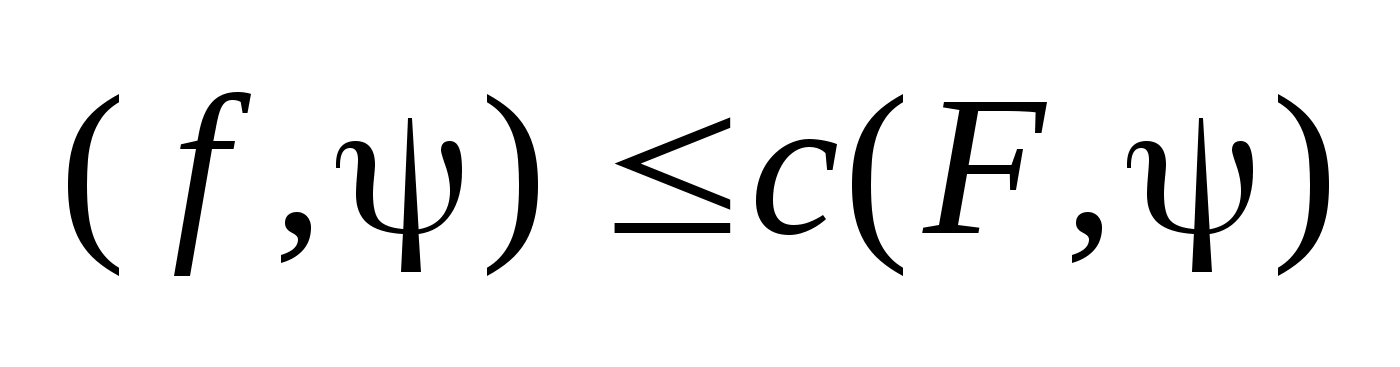 ,
когда
,
когда
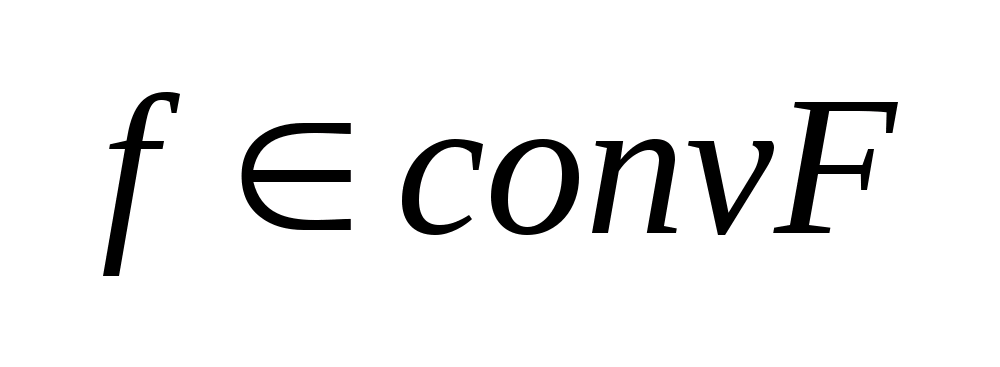 .
Следствие: Точка
.
Следствие: Точка
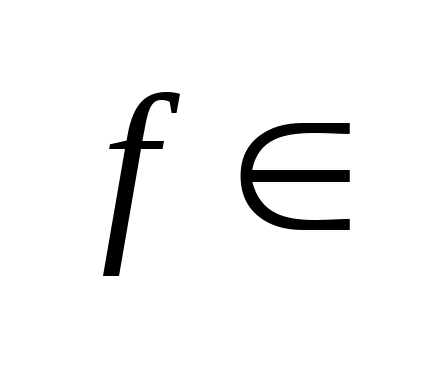 выпуклому мн-ву
выпуклому мн-ву
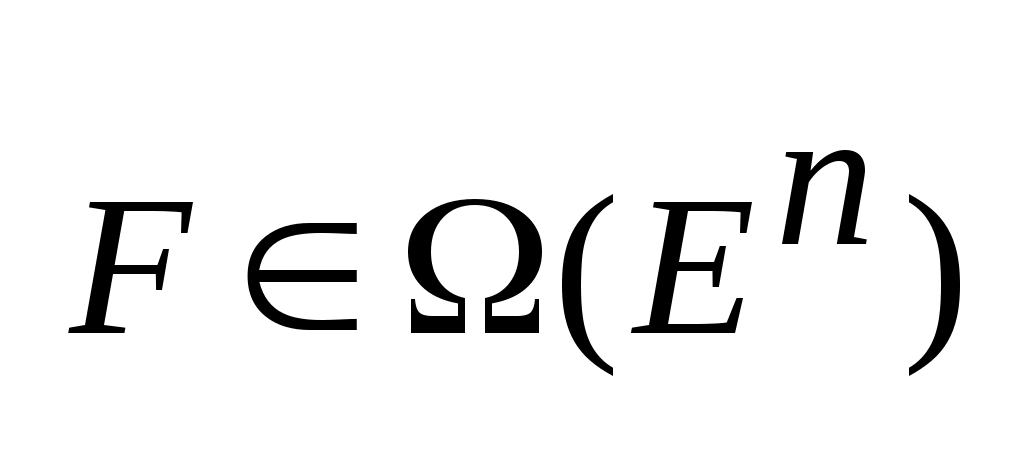 , тогда и только тогда , когда
, тогда и только тогда , когда
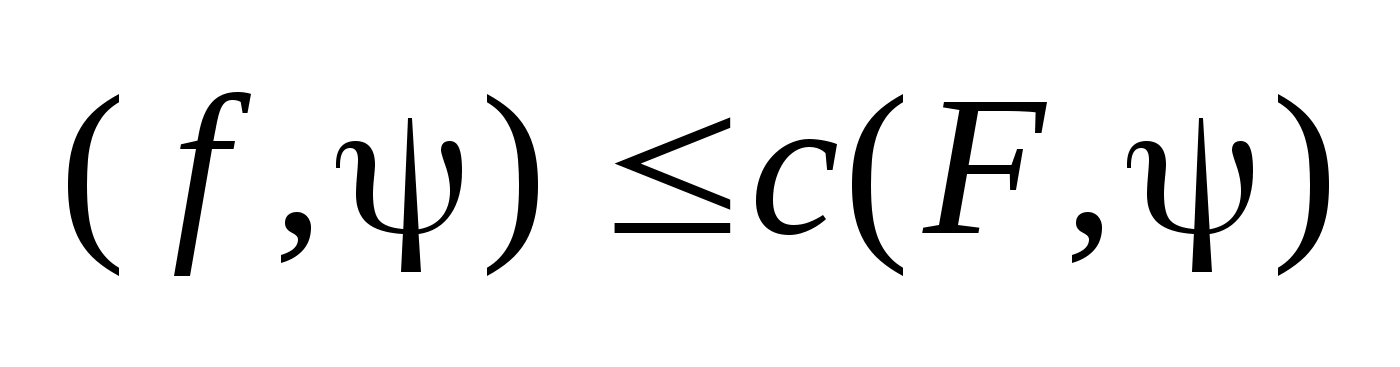 .
.
10.
Пусть
задано множество
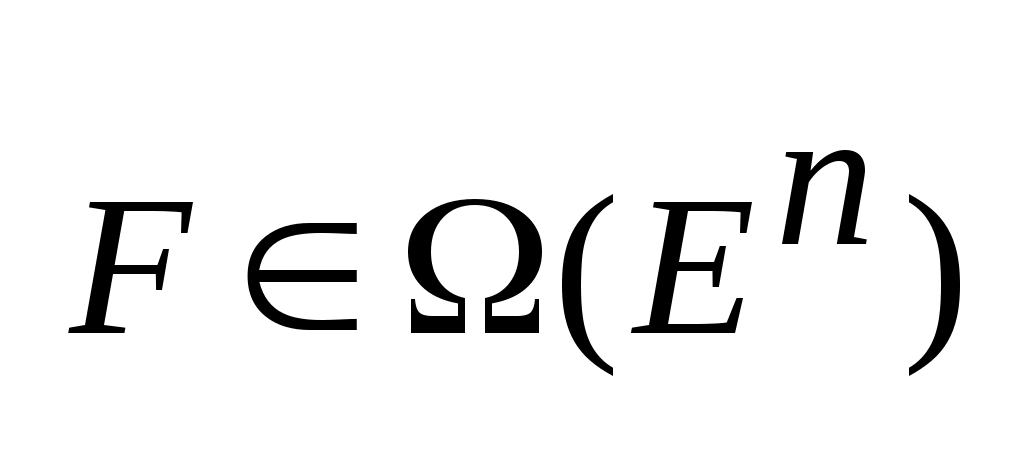 ,
а
,
а
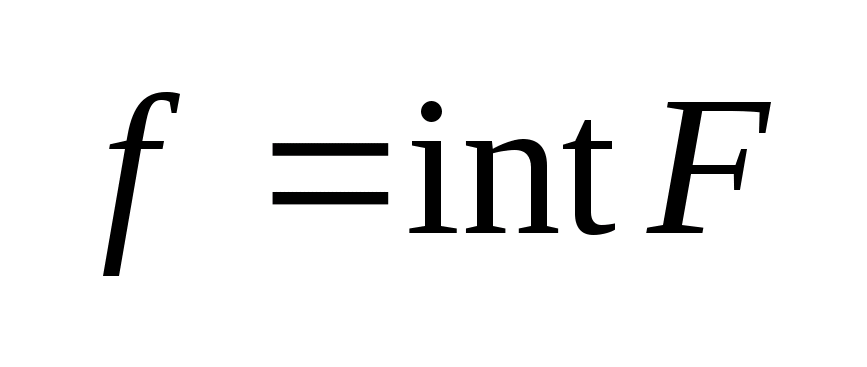 ,
тогда
,
тогда
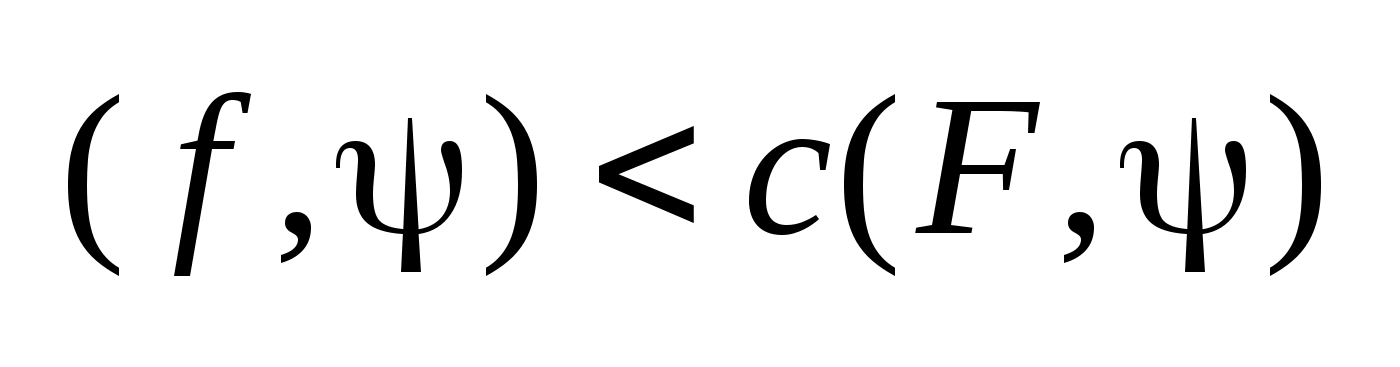 .
.
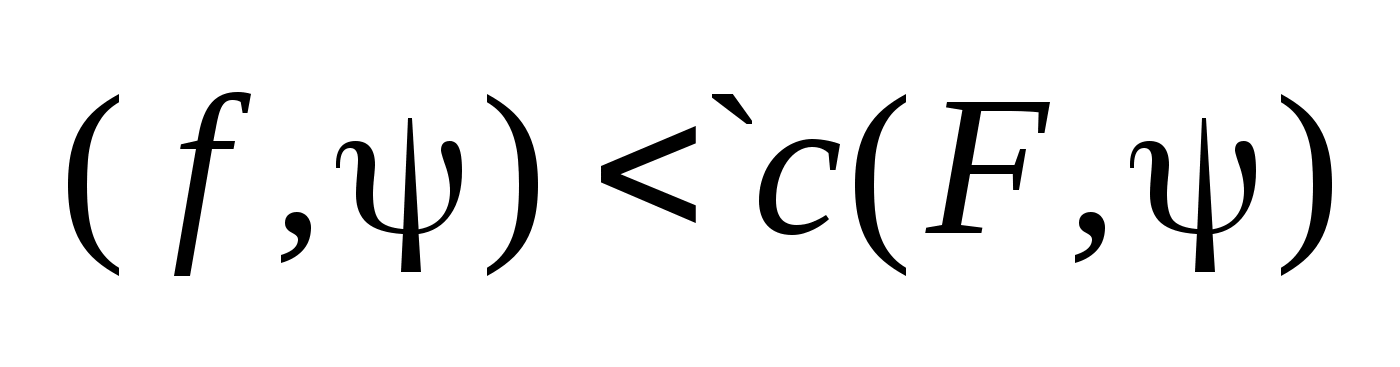
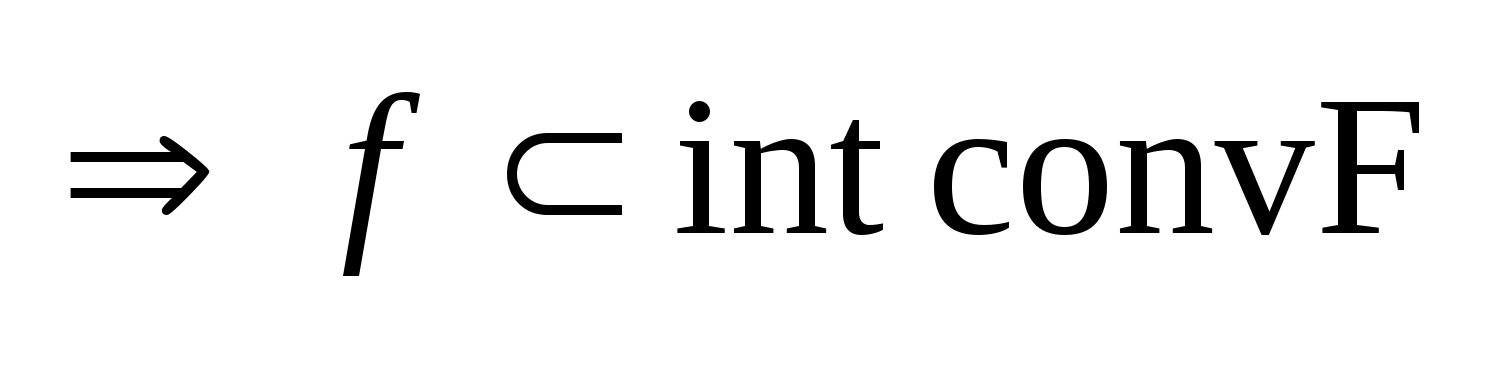 .
Следствие: Пусть задано множество
.
Следствие: Пусть задано множество
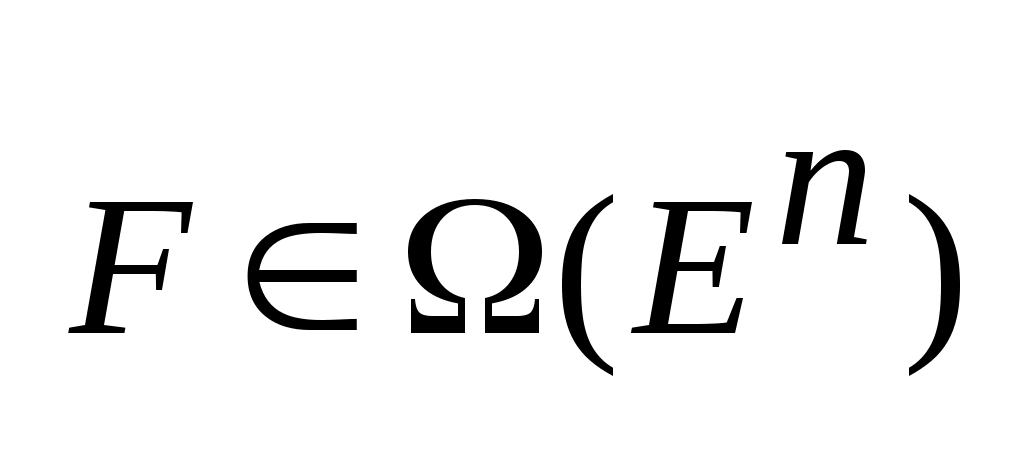 ,
,
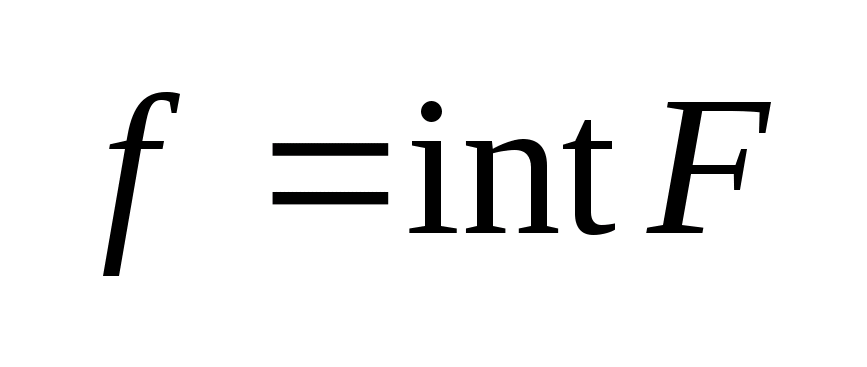 ,
тогда и только тогда, когда
,
тогда и только тогда, когда
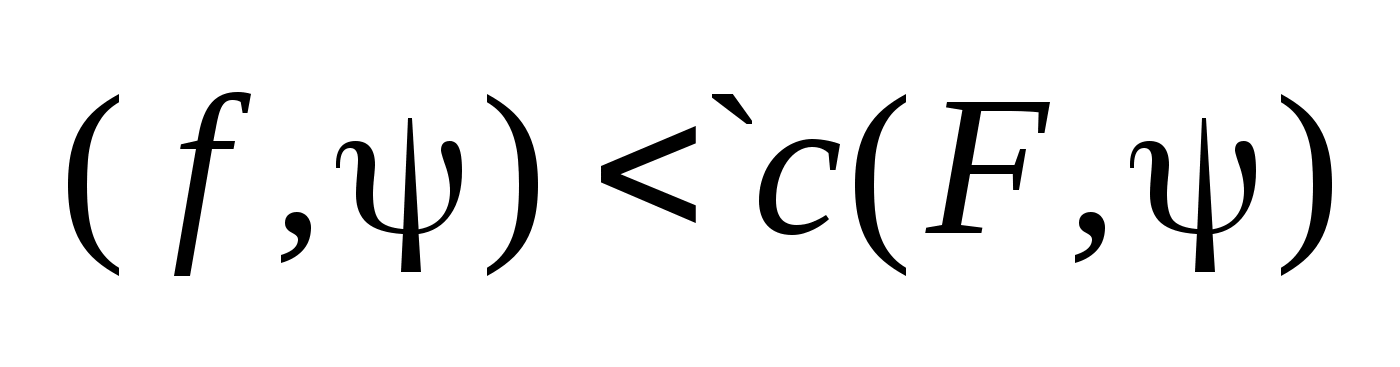 .
.
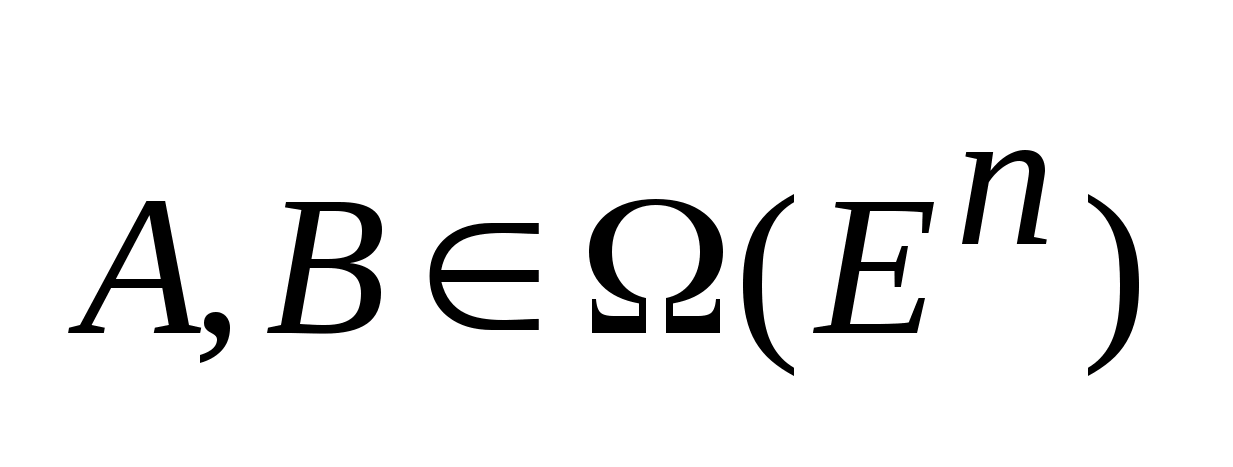 и
если
и
если
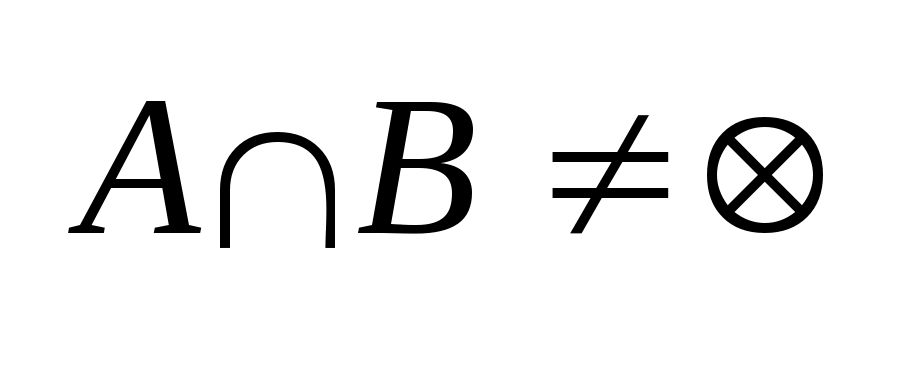 ,
то
,
то
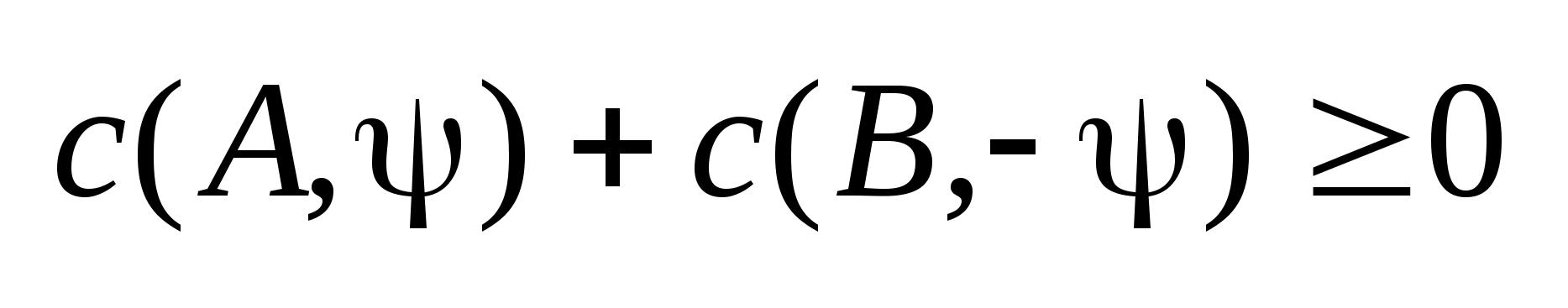 .
И наоборот: Если
.
И наоборот: Если
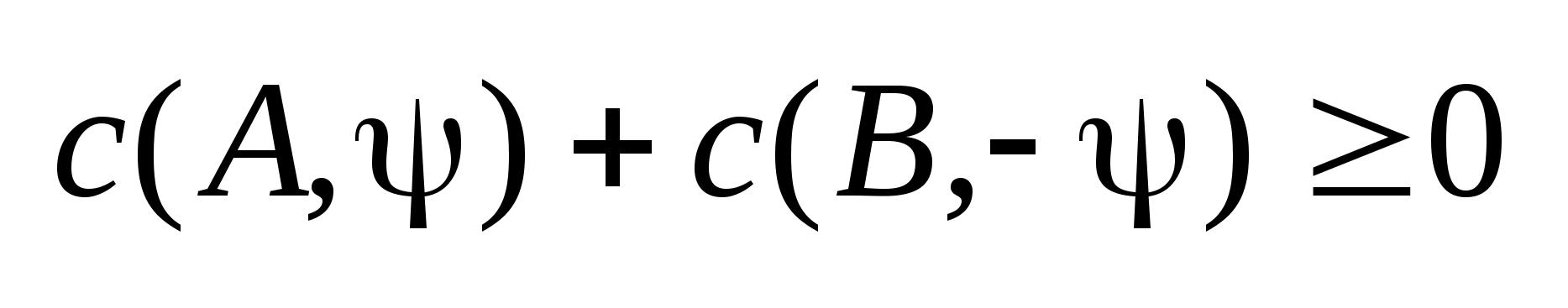 ,то
,то
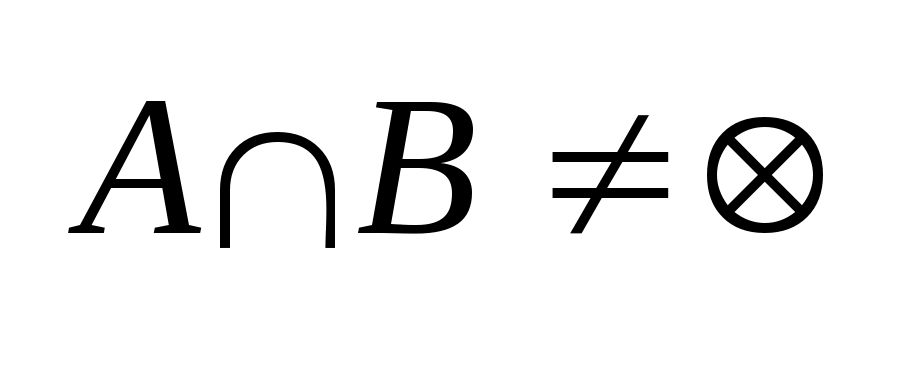 .Следствие:
Два вып. Мн-ва пересекаются тогда и
только тогда, когда
.Следствие:
Два вып. Мн-ва пересекаются тогда и
только тогда, когда
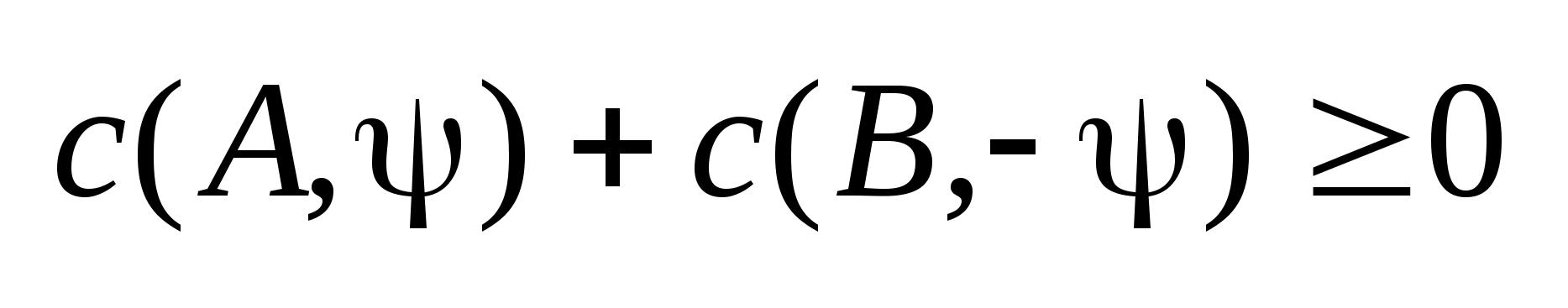 .
.
8. Непрерывные функции. Условия Липшица. Лемма 1,2 об условиях Липшица для опорных функций.
Пусть
 -два
метрических пространства с метриками
-два
метрических пространства с метриками
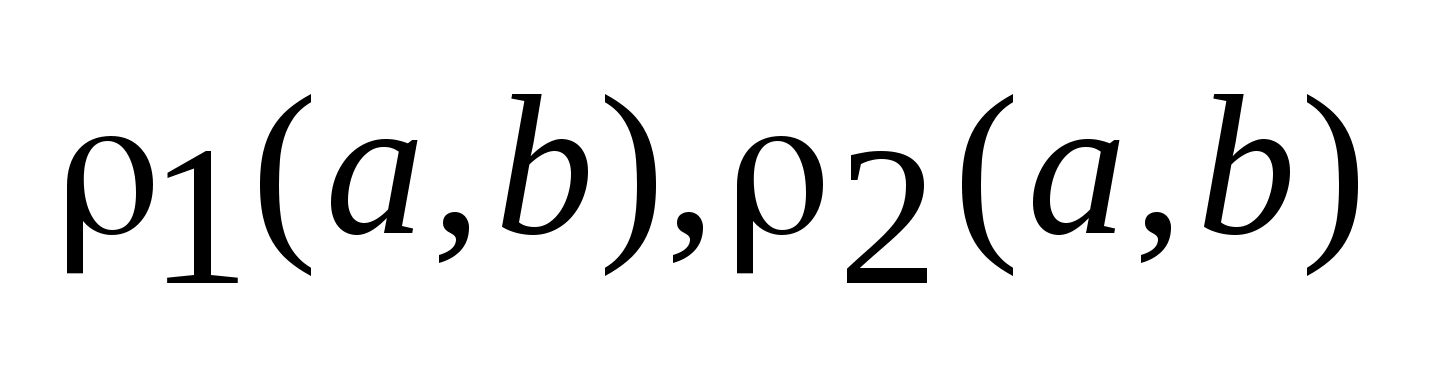 и
пусть f
отображает
и
пусть f
отображает
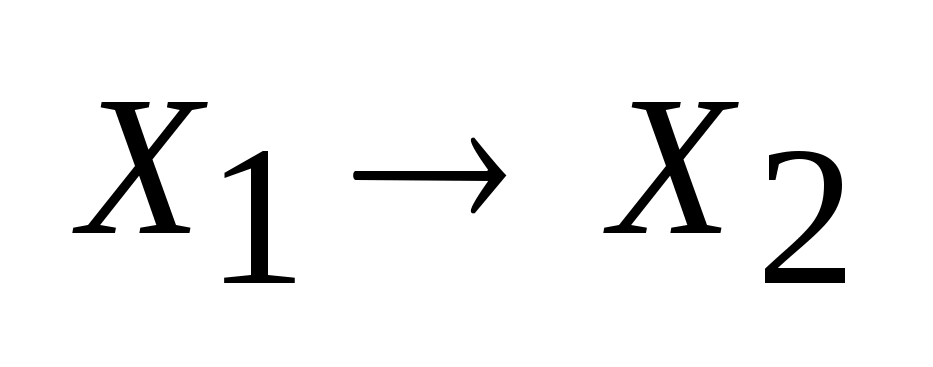 .
f
непрерывна
в точке
.
f
непрерывна
в точке
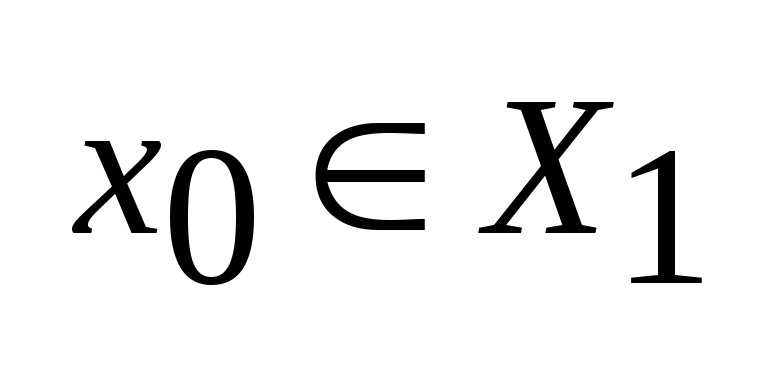 ,
если
,
если
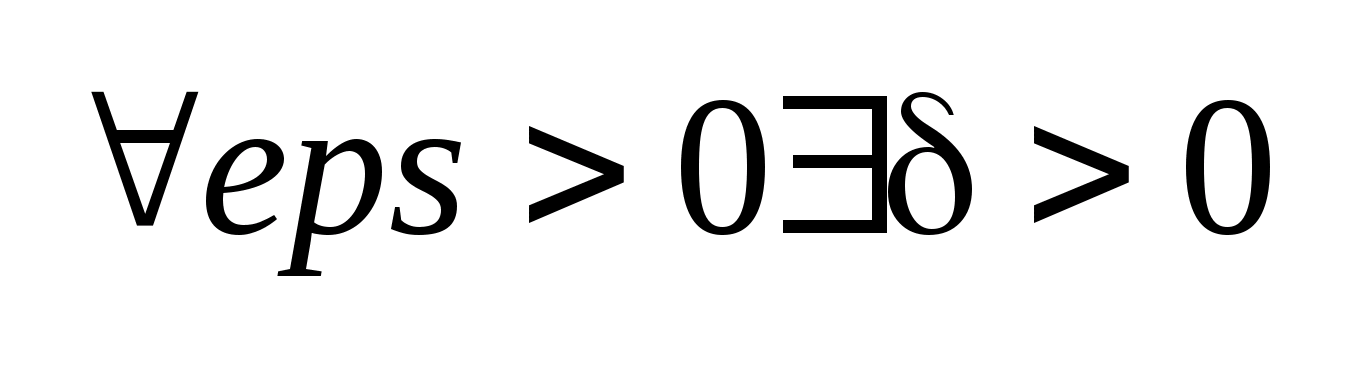 такое
что
такое
что
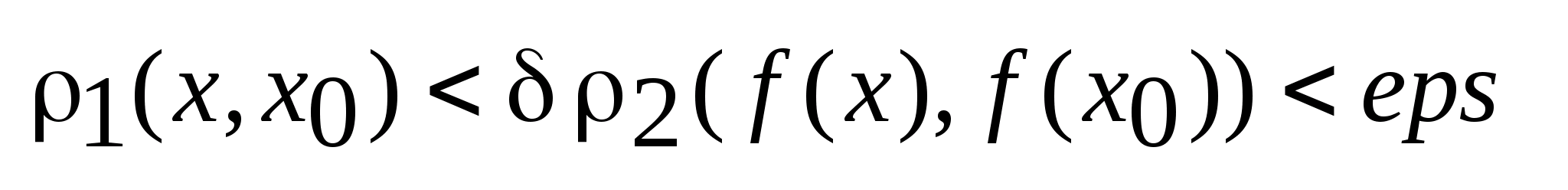 Условие
Липшица:
Функция f,
отображающая
Условие
Липшица:
Функция f,
отображающая
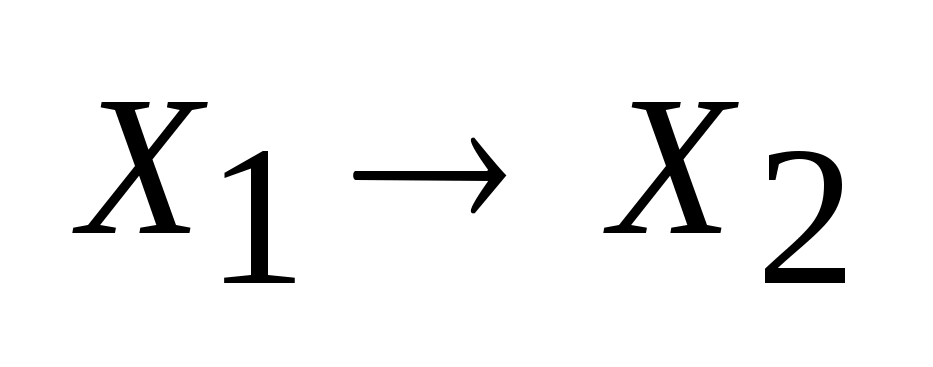 ,
удовлетворяет условию Липшица с const
L
, если для любых двух точек
,
удовлетворяет условию Липшица с const
L
, если для любых двух точек
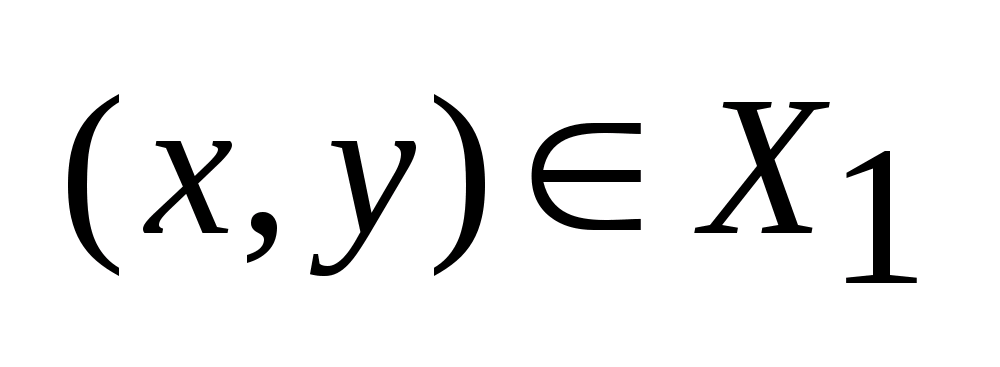 ,
выполняется неравенство
,
выполняется неравенство
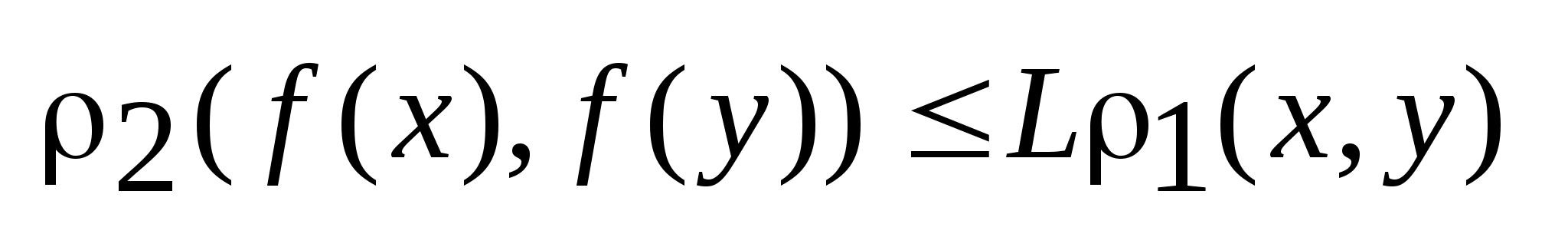 ,для опорных функций
,для опорных функций
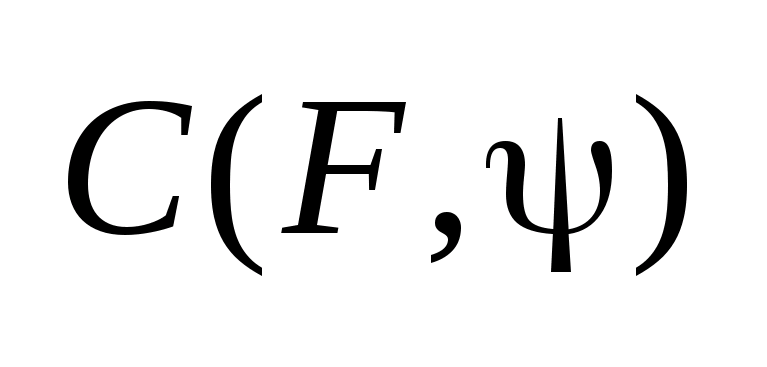 ,
,
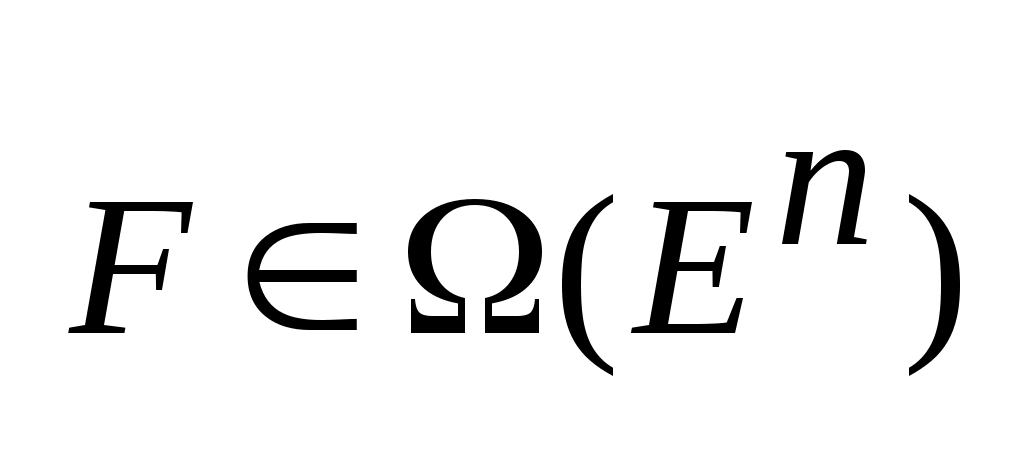 ,
,
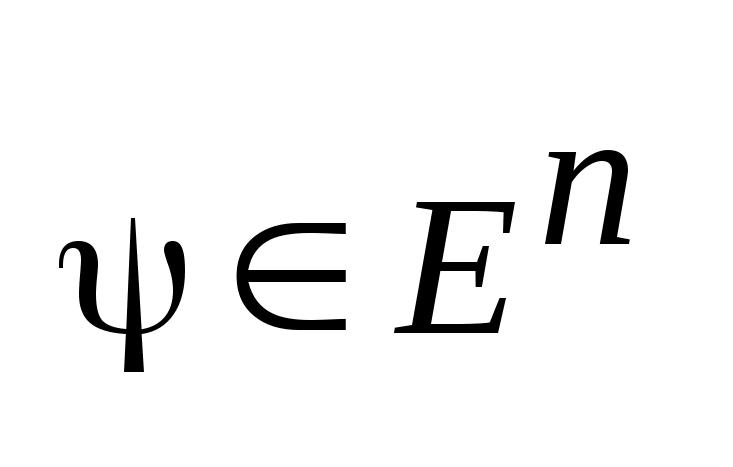 :
: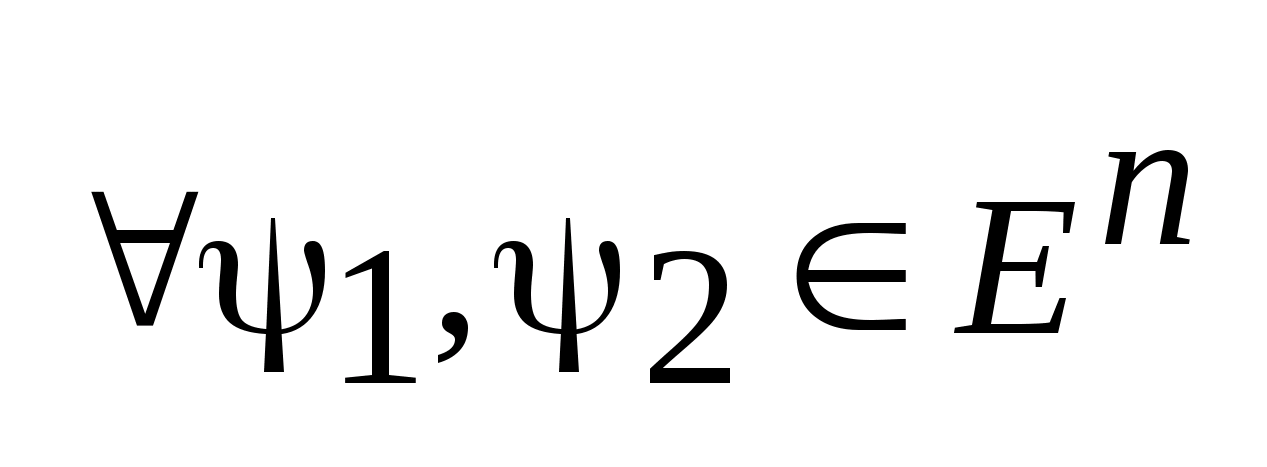
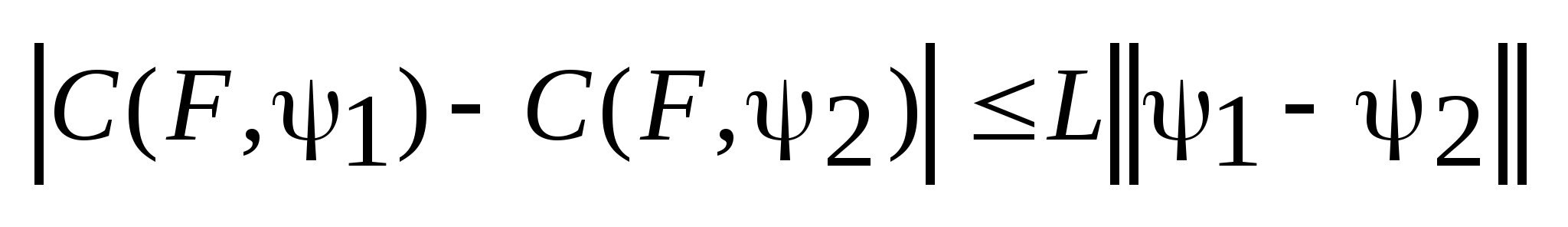
Лемма:
Опорная функция
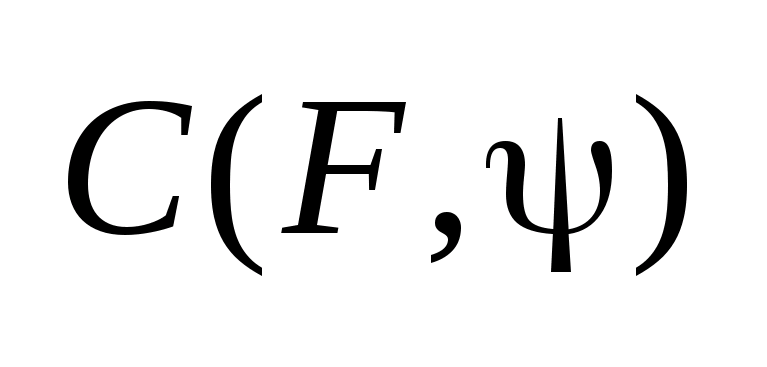 удовлетворяет условию Липшеца по f
с const
L=
удовлетворяет условию Липшеца по f
с const
L= .
.
Лемма:
Пусть
 -
выпуклы, тогда хаусдорффова норма
-
выпуклы, тогда хаусдорффова норма
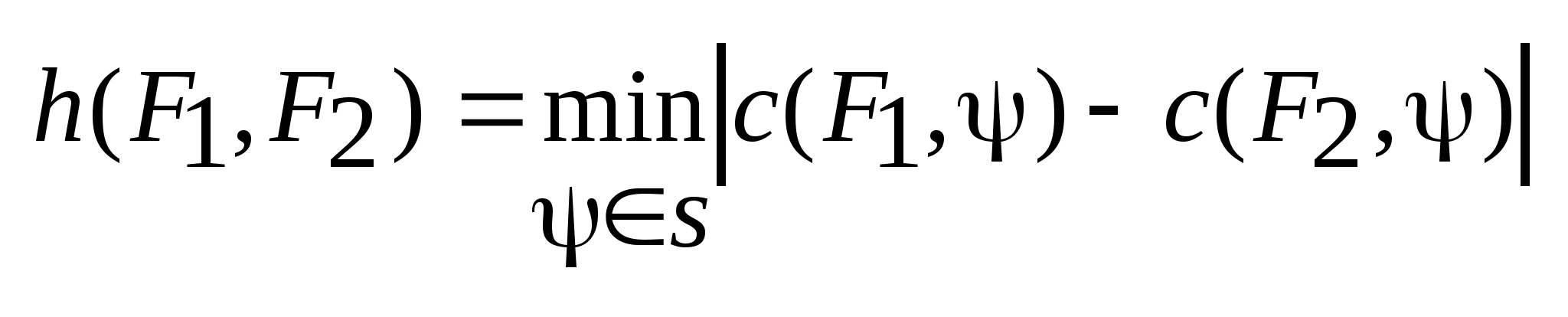
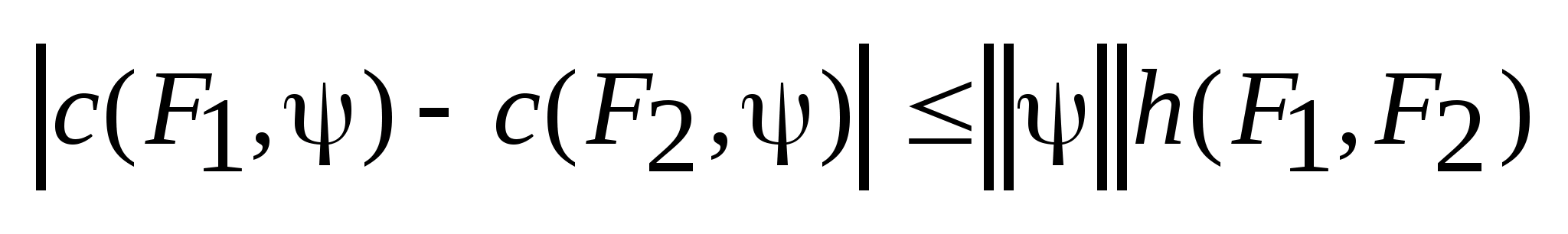
9. Многозначные отображения.
Многозначным
отображением будем называть функцию
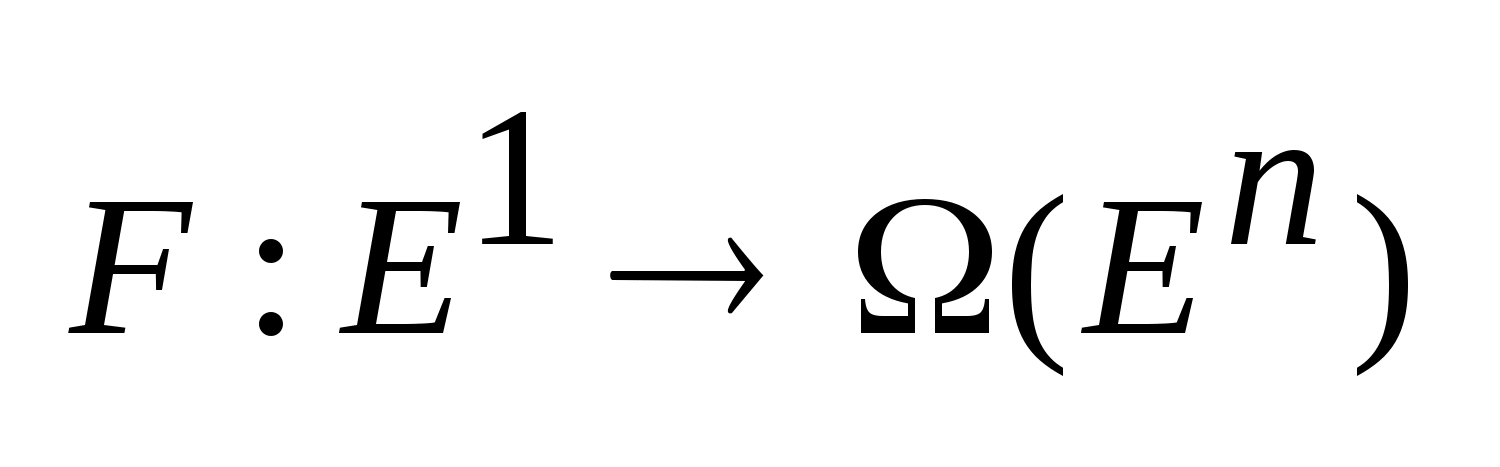 у
которой аргументом является число, а
значением некоторые множества
у
которой аргументом является число, а
значением некоторые множества
10. Непрерывные и равномерно непрерывные многозначные отображения.
Многозначное
отображение
F(t)
непрерывно в точке
 ,
если для
,
если для
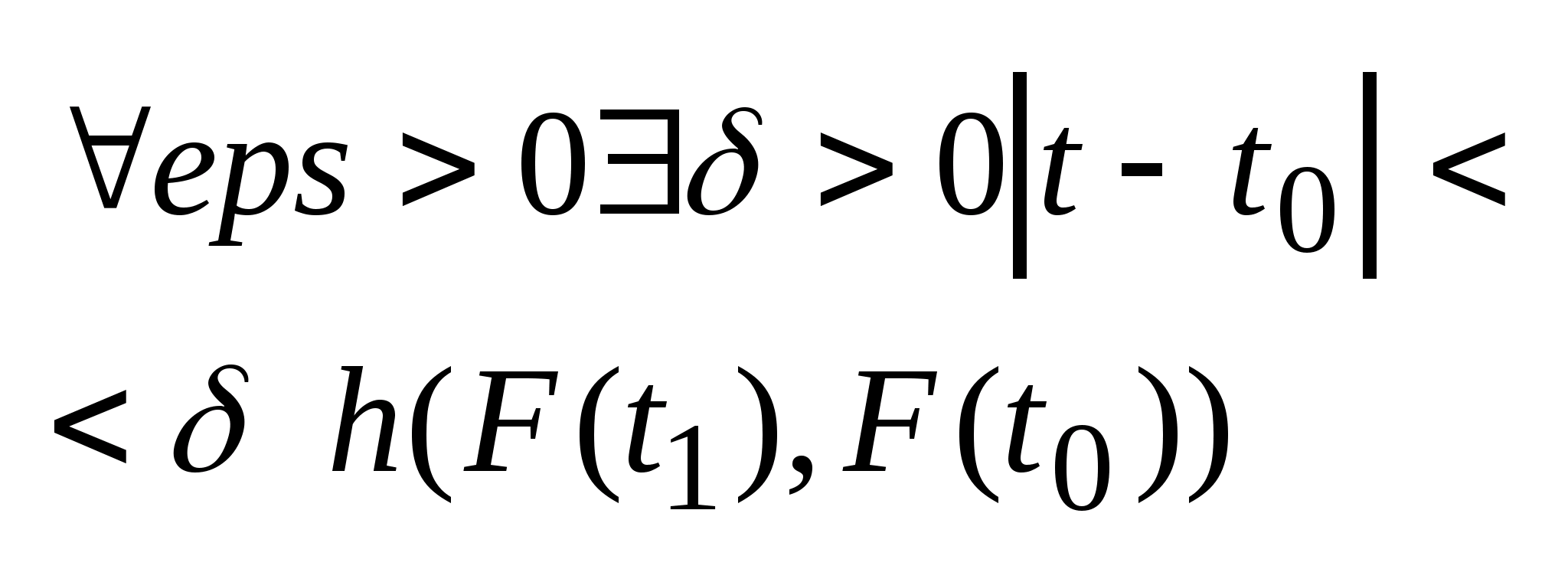 .
.
Лемма:
Пусть
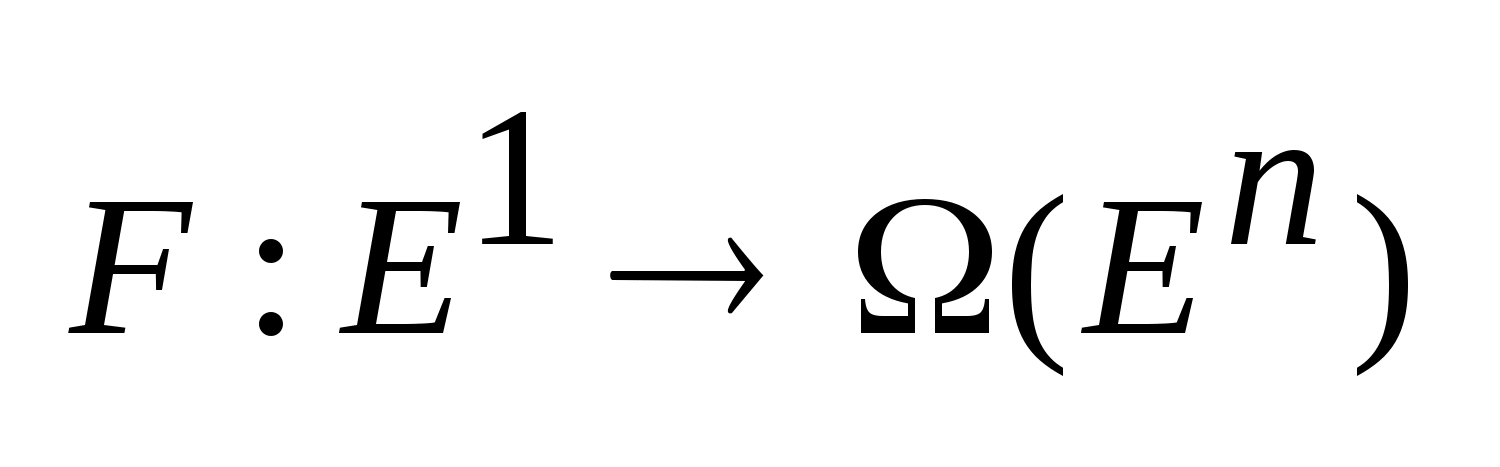 непрерывное
многозначное отображение , когда
непрерывное
многозначное отображение , когда
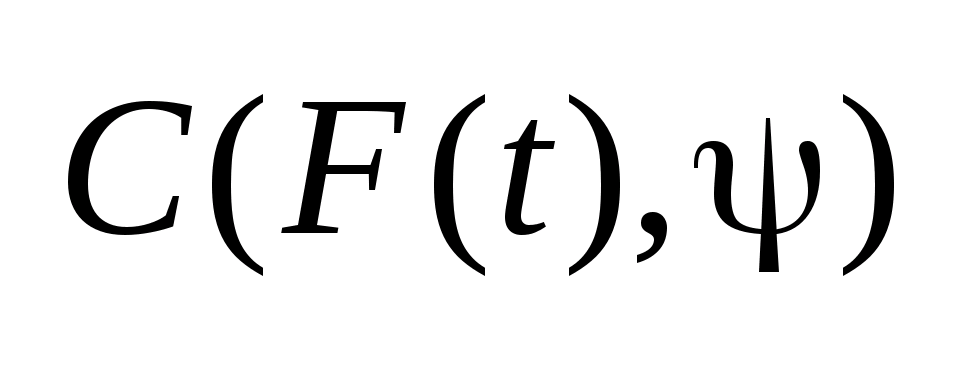 непрерывна
по t
при всяком фиксированном
непрерывна
по t
при всяком фиксированном
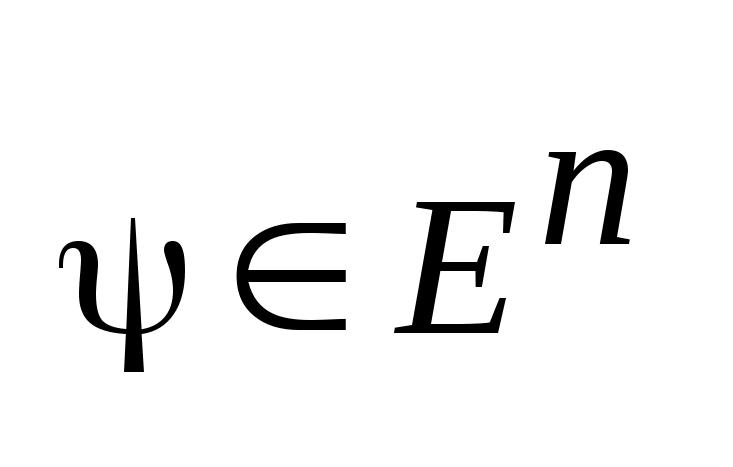 ,
более того
,
более того
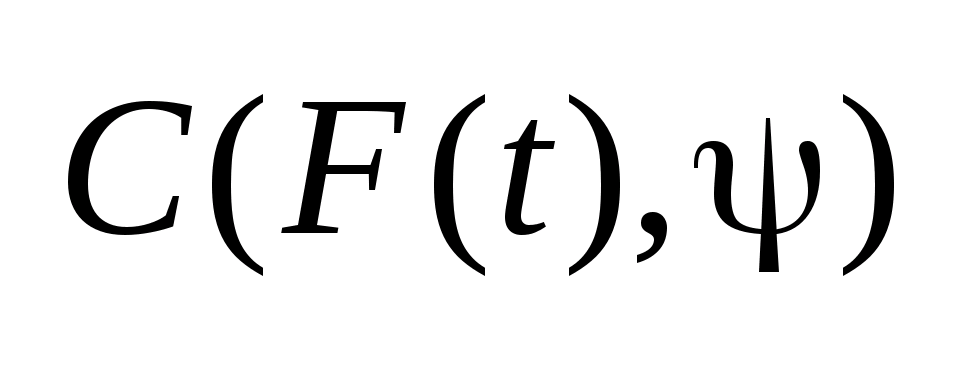 равномерно
непрерывно по t
равномерно
непрерывно по t
 .
.
Если
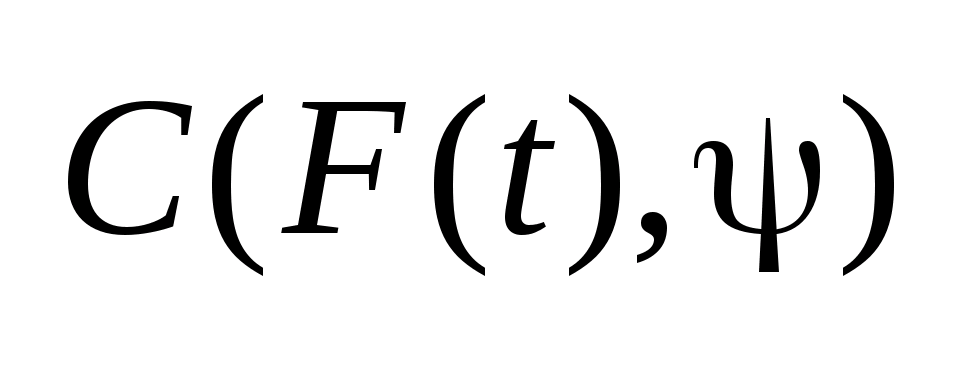 равномерно непрерывно по t
равномерно непрерывно по t
 ,
то многозначное отображение conv
F(t) непрерывно.
,
то многозначное отображение conv
F(t) непрерывно.
11. Измеримые многозначные отображения. Лемма о равномерной непрерывности многозначного отображения.
Функция
f(t)
отображающая
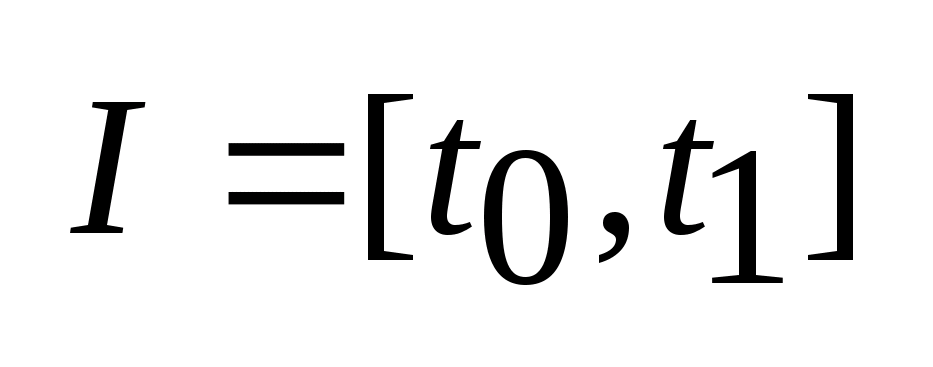 в
некоторое метрическое пр-во
в
некоторое метрическое пр-во
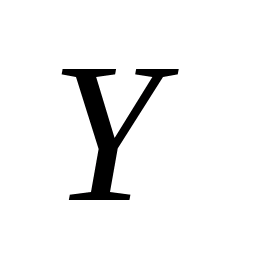 с
метрикой
с
метрикой
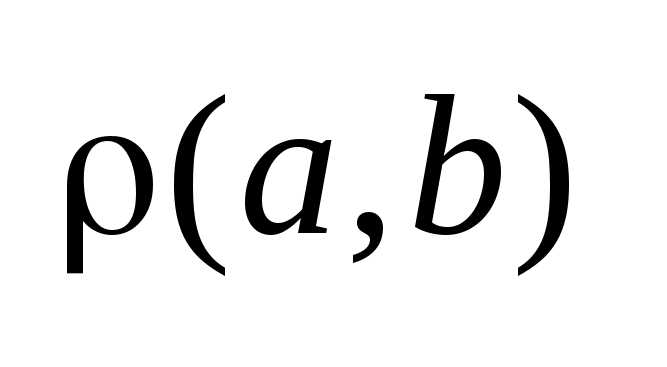 называется
измеримой, если праобраз любого шара
называется
измеримой, если праобраз любого шара
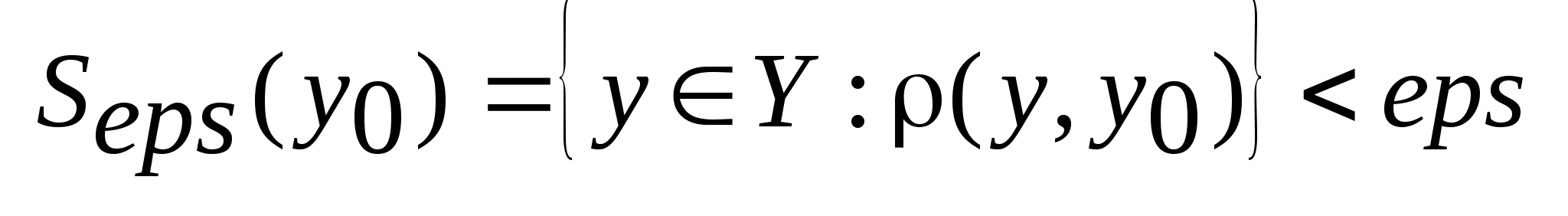 есть
мн-во измеримое.
есть
мн-во измеримое.
12. Интеграл от многозначного отображения. Теорема о непрерывности от многозначного отображения.
F-многозначное
отображение, такое что F:
I
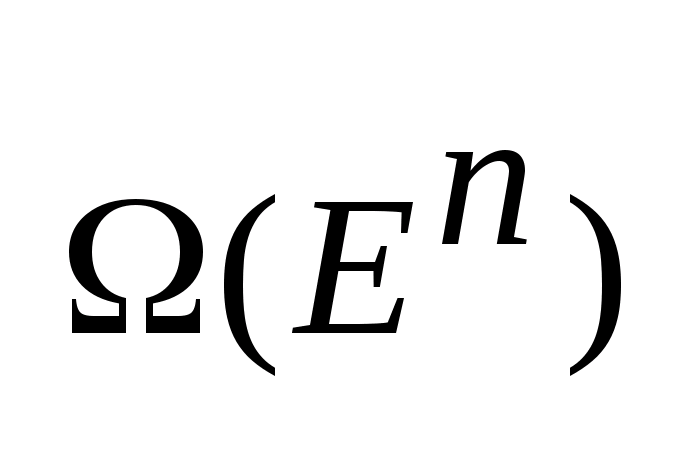 ,
где
,
где
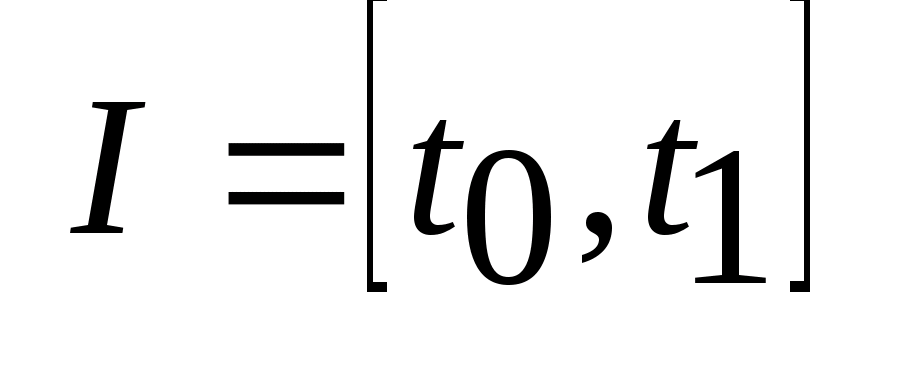 ,
,
 -замкнутое,
ограниченное, не пустое, компактное
множество.
-замкнутое,
ограниченное, не пустое, компактное
множество.
Интегралом
от многозначного отображения на отрезке
I
называется множество G
(G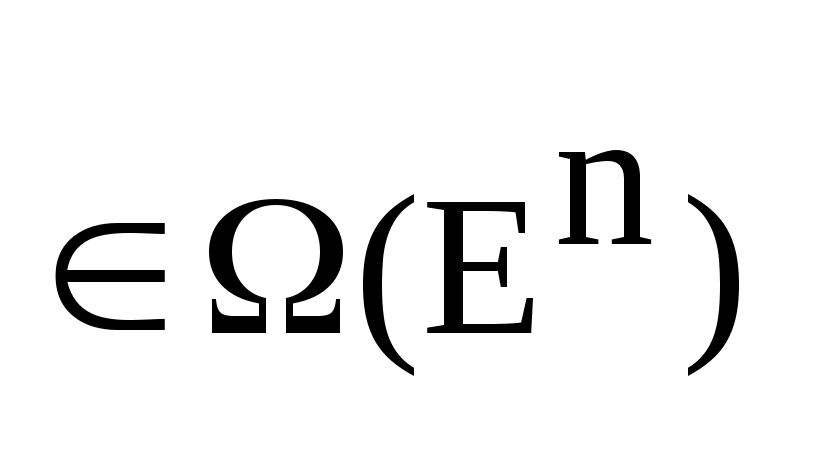 )
вида:
)
вида:
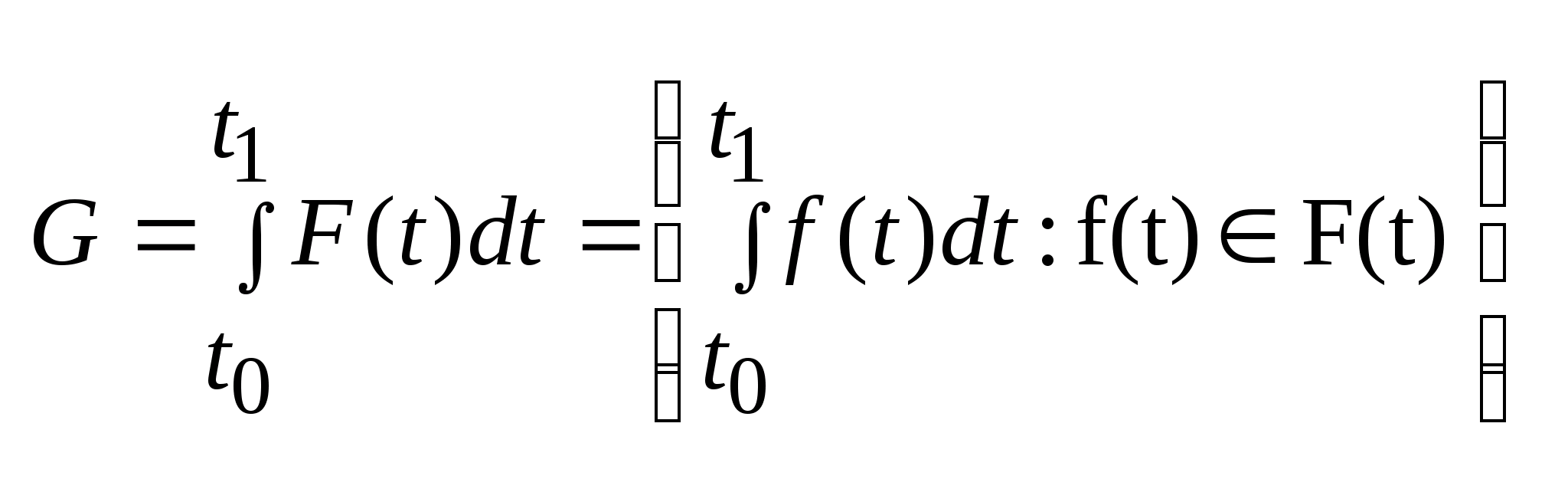 .
Это мн-во значений интеграла по всем
однозначным ветвям отображения
.
Это мн-во значений интеграла по всем
однозначным ветвям отображения
F(t) .
Теорема
3:
Пусть многозначное
отображение F(t)
измеримо и удовлетворяет условию:
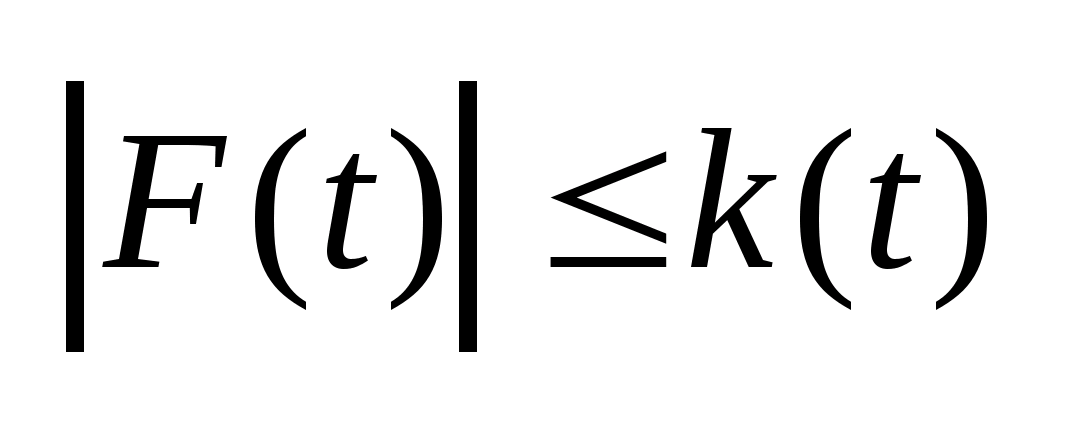 ,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда
,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда
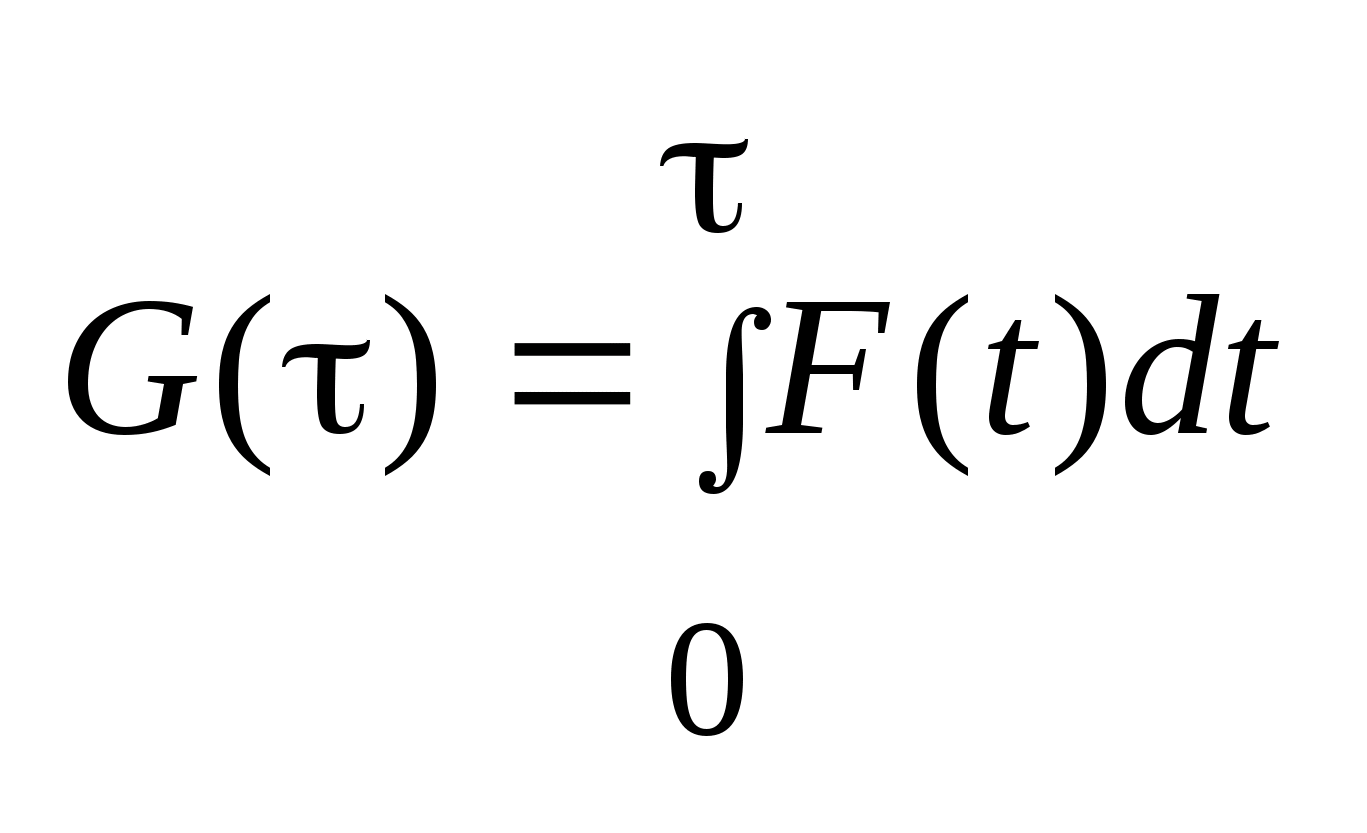 непрерывна
на отр. I
.
непрерывна
на отр. I
.
Опорная
функция
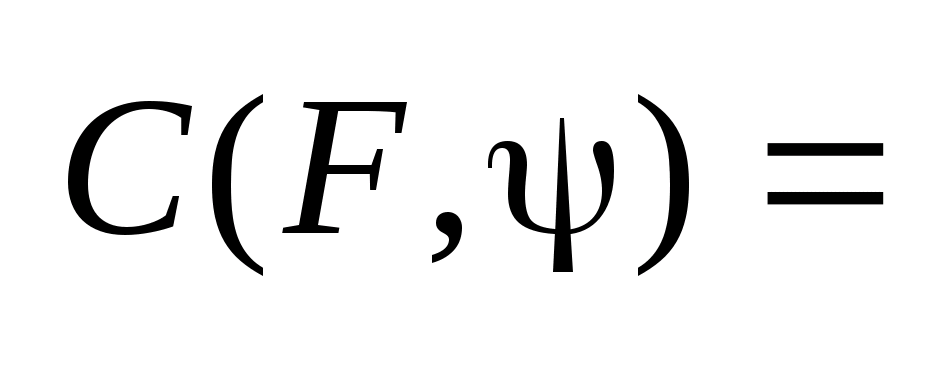
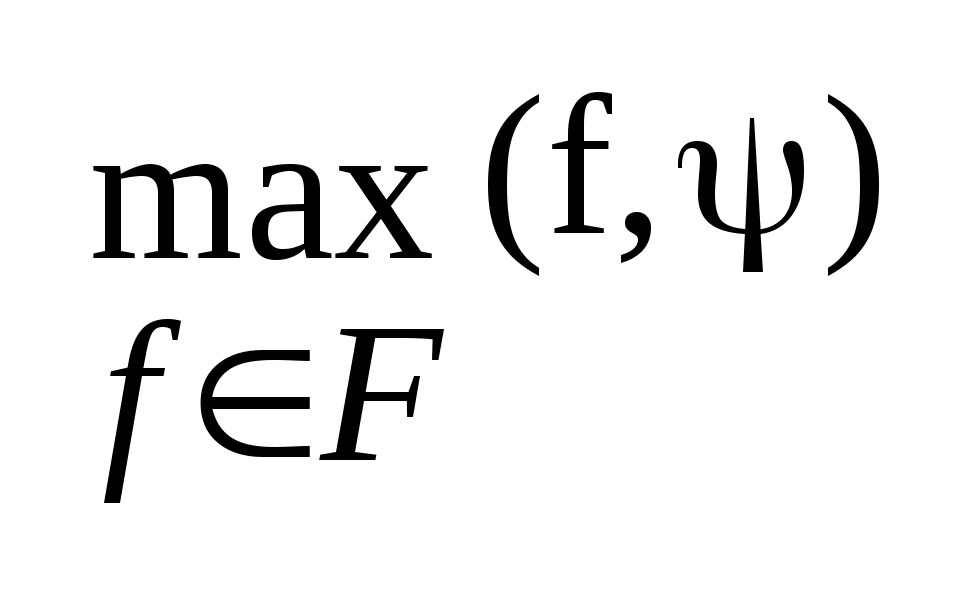 ,
где
F
,
где
F ,
,
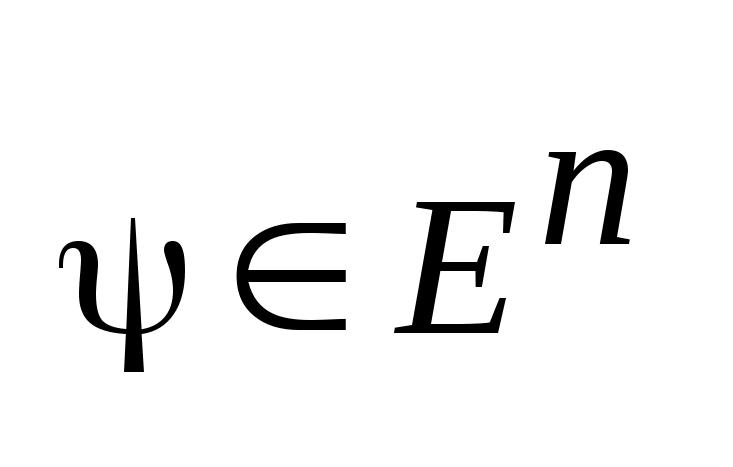 .
.
13. Теоремы 1, 2 о других видах многозначных отображений.
F-многозначное
отображение, такое что F:
I
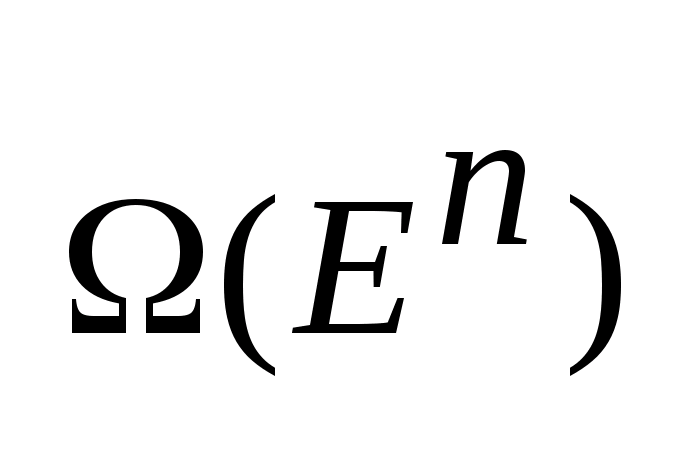 ,
где
,
где
 ,
,
 -замкнутое,
ограниченное, не пустое, компактное
множество.
-замкнутое,
ограниченное, не пустое, компактное
множество.
Интегралом
от многозначного отображения на отрезке
I
называется множество G
(G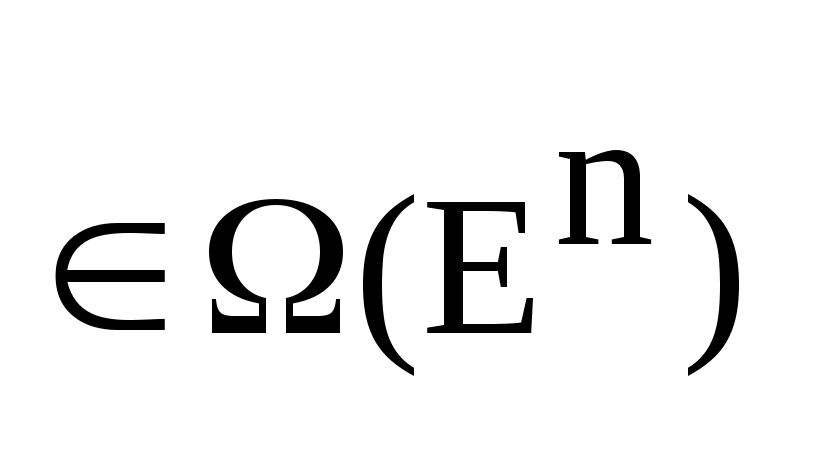 )
вида:
)
вида:
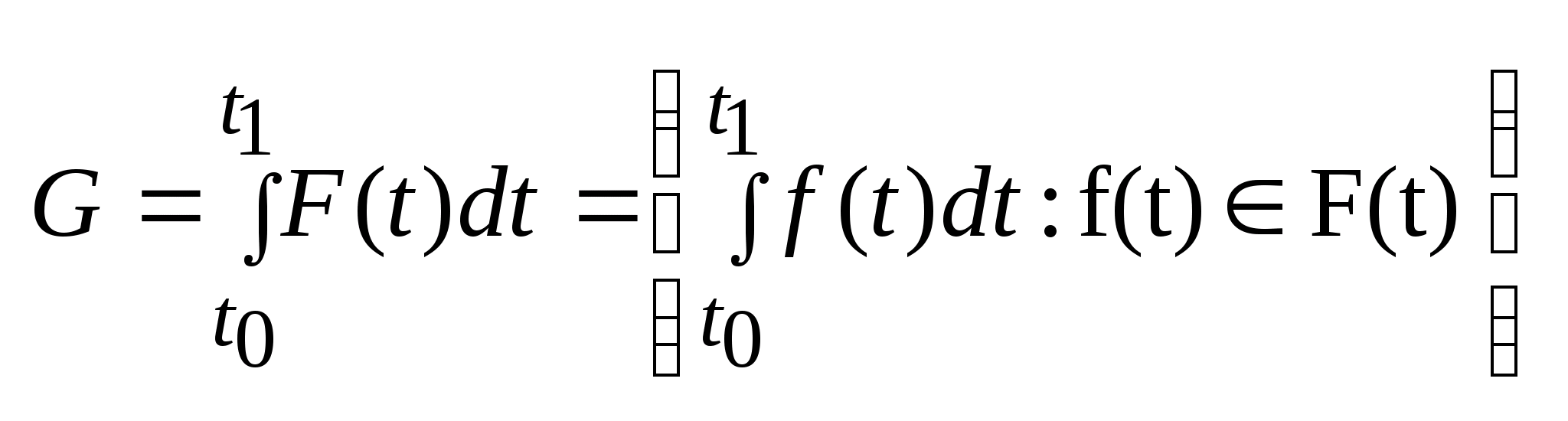 .
Это мн-во значений интеграла по всем
однозначным ветвям отображения
.
Это мн-во значений интеграла по всем
однозначным ветвям отображения
F(t) .
Теорема
1:
Пусть
многозначное отображение F(t)
измеримо и удовлетворяет условию:
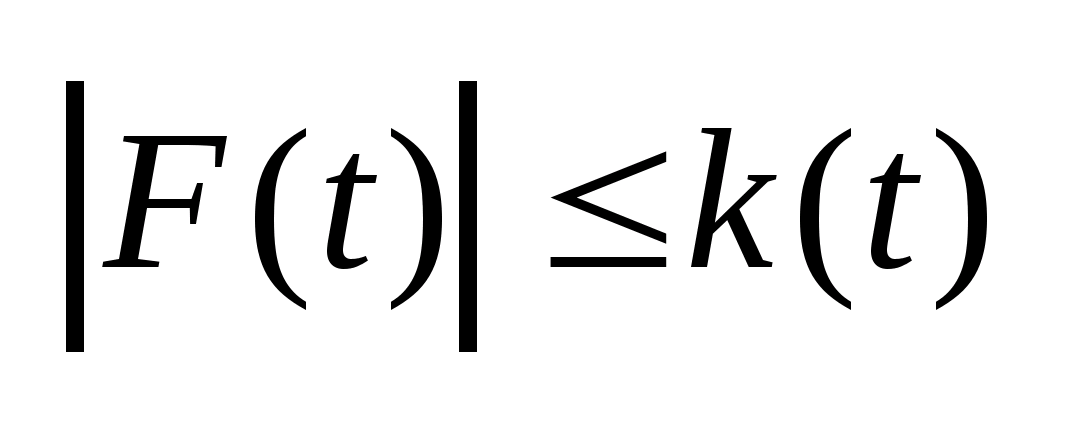 ,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда
G является
не пустым, компактным множеством в
пространстве
,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда
G является
не пустым, компактным множеством в
пространстве
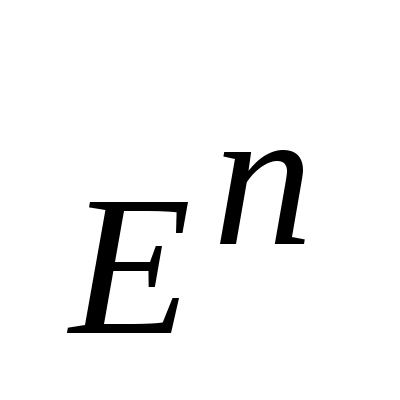 ,
,
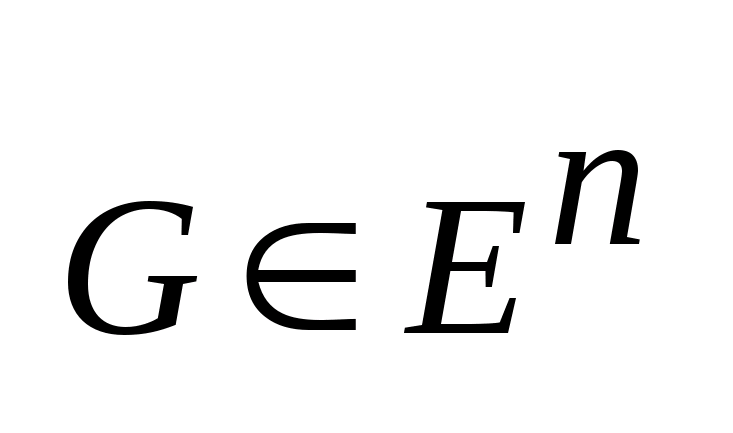 и
выпукло.
и
выпукло.
Теорема
2 :
Пусть
многозначное отображение F(t)
измеримо и удовлетворяет условию:
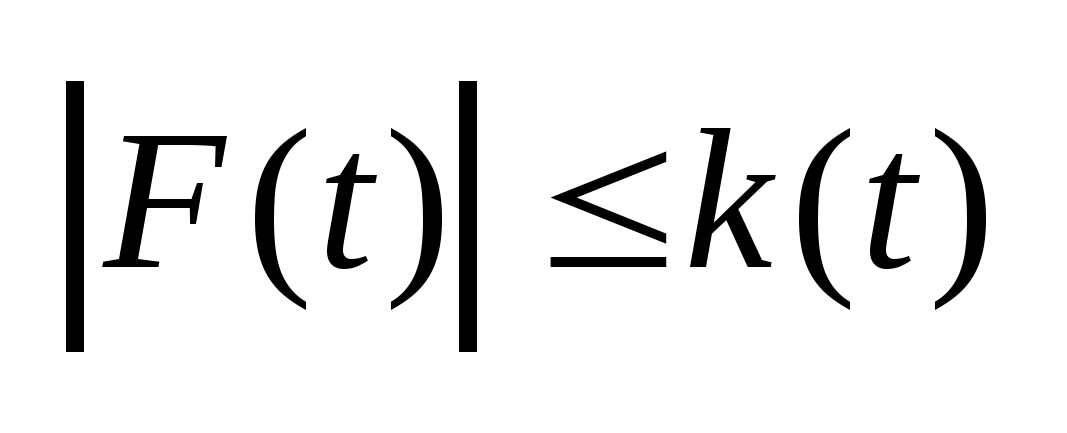 ,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда опорная функция
,
где k(t)-
скалярная функция, интегрируемая по
Лебегу на отрезке I и
измерима, тогда опорная функция
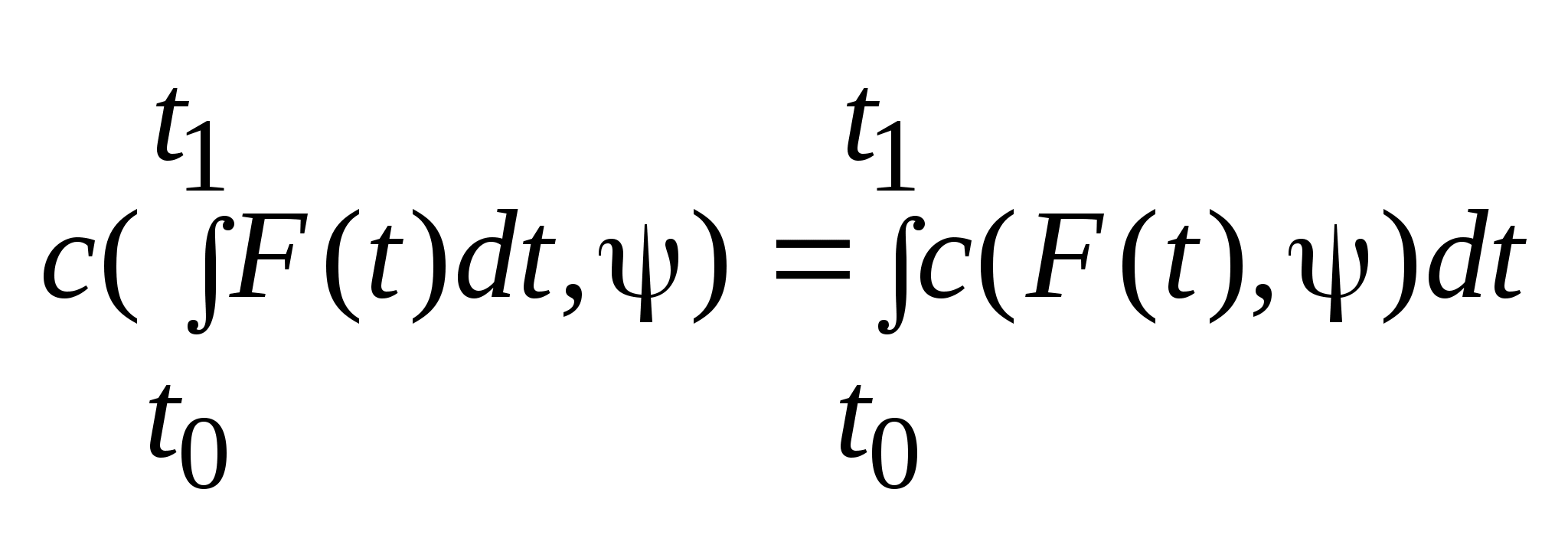 .
.
14. Линейная задача быстродействия. Определение абс. непрерывной функции. Теорема Каратеодори.
Рассматриваем
динамический объект, поведение которого
описывается системой (1)
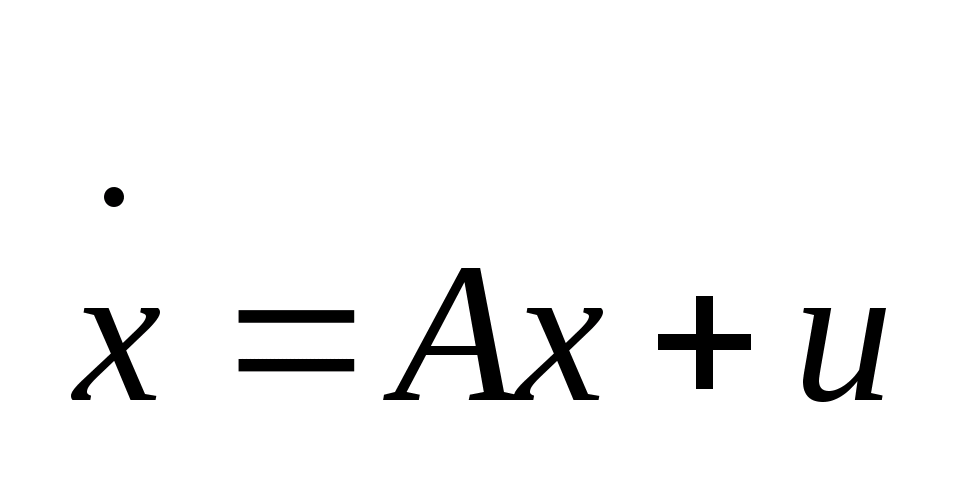 ,
x-
n-мерный
вектор,
,
x-
n-мерный
вектор,
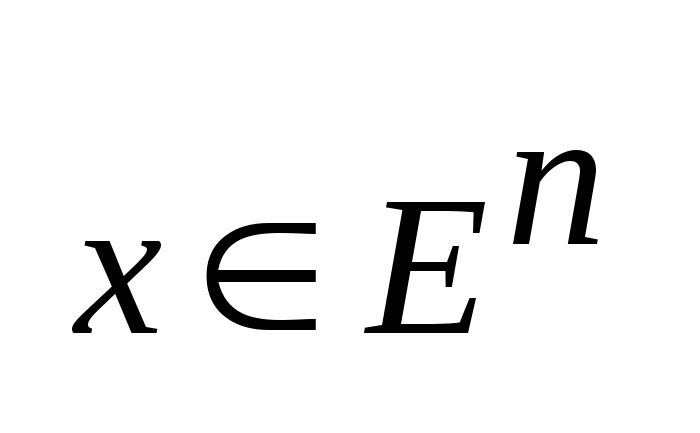 ,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
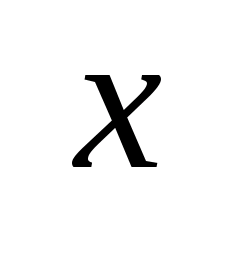 ,
,
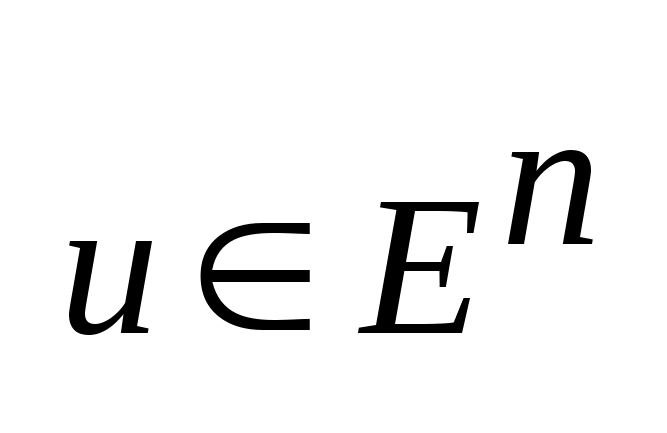 .Задано
.Задано
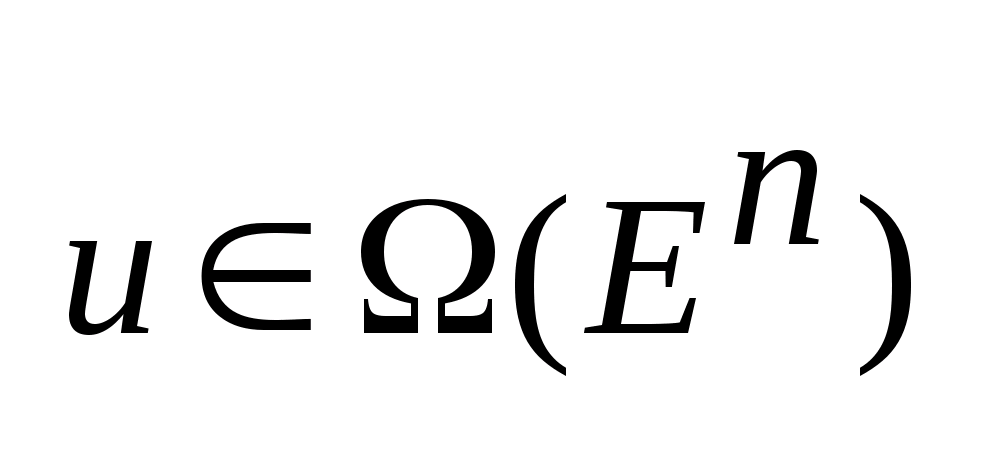 ,
u:
I
,
u:
I
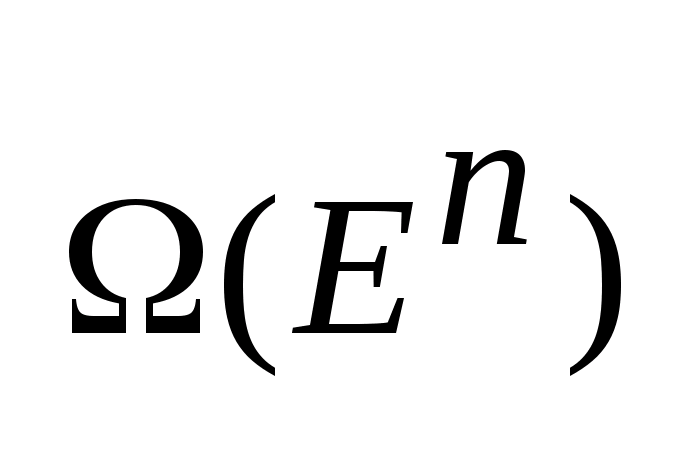 и полагается, что u(t)
измеримо
и
и полагается, что u(t)
измеримо
и
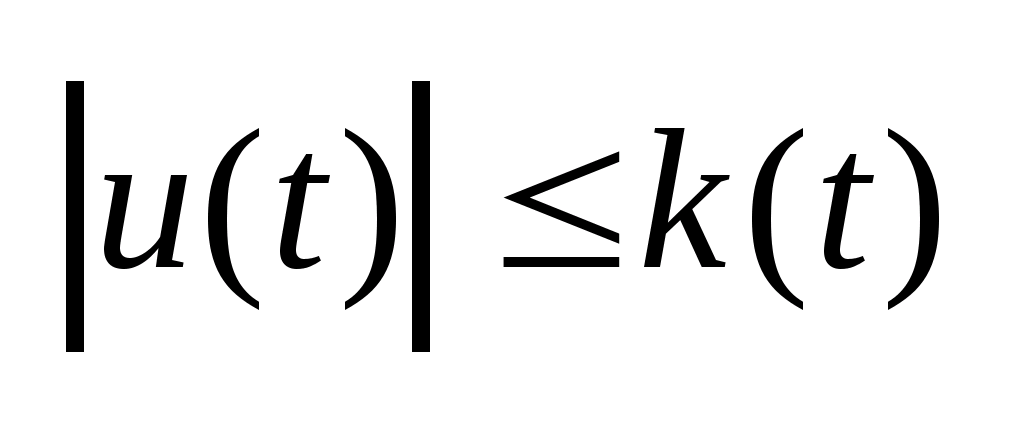 -
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью
(2)
u(t)
-
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью
(2)
u(t)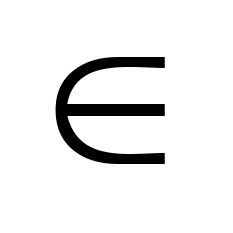 U(t)
-
ограничения на управления . В фазовом
пространстве
U(t)
-
ограничения на управления . В фазовом
пространстве
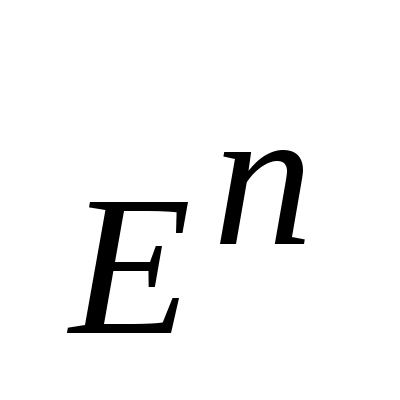 заданы
два не пустых множества
заданы
два не пустых множества
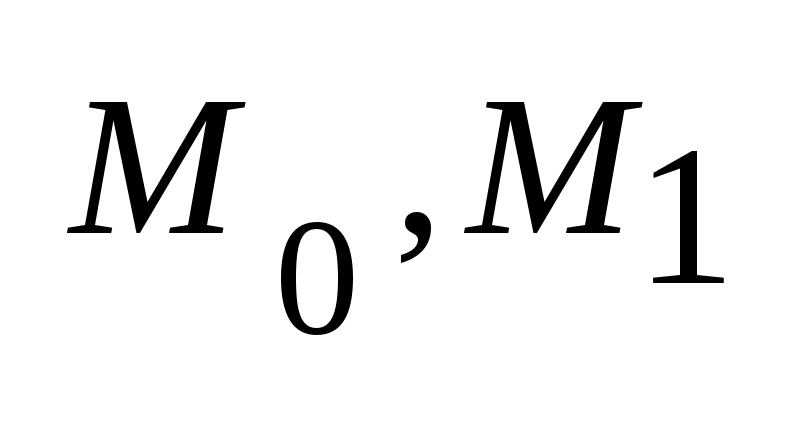
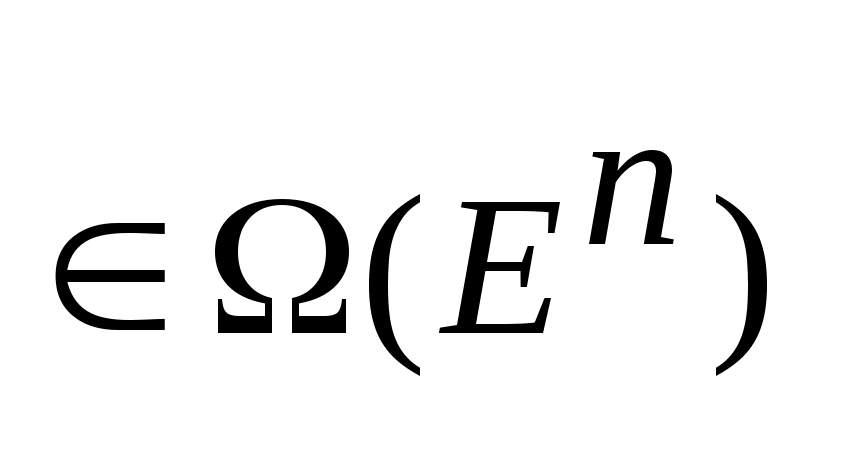 .
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
 в конечное множество
в конечное множество
 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
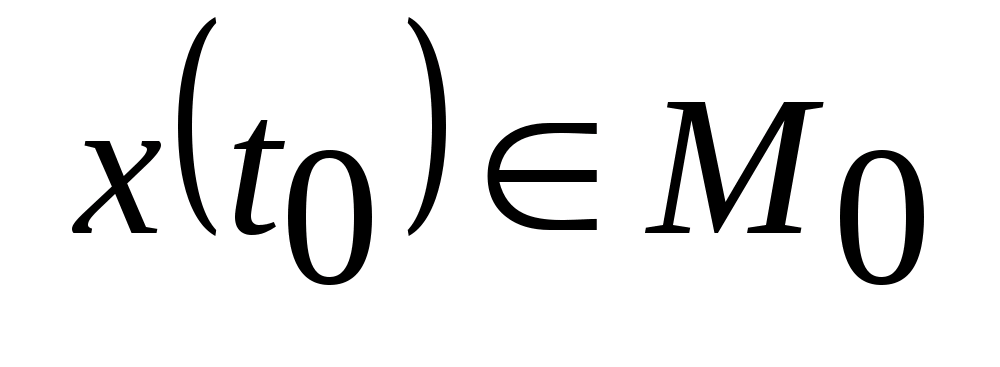 и
и
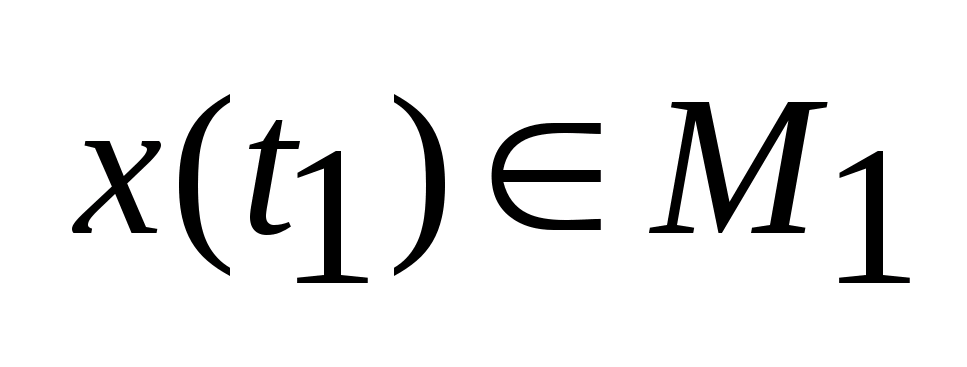 .
Цель управления- перевод динамический
объекта из
.
Цель управления- перевод динамический
объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача
быстродействия заключается в нахождении
такого допустимого управления, которое
осуществляет переход из множества
 в
в
 за
наименьшее время.
за
наименьшее время.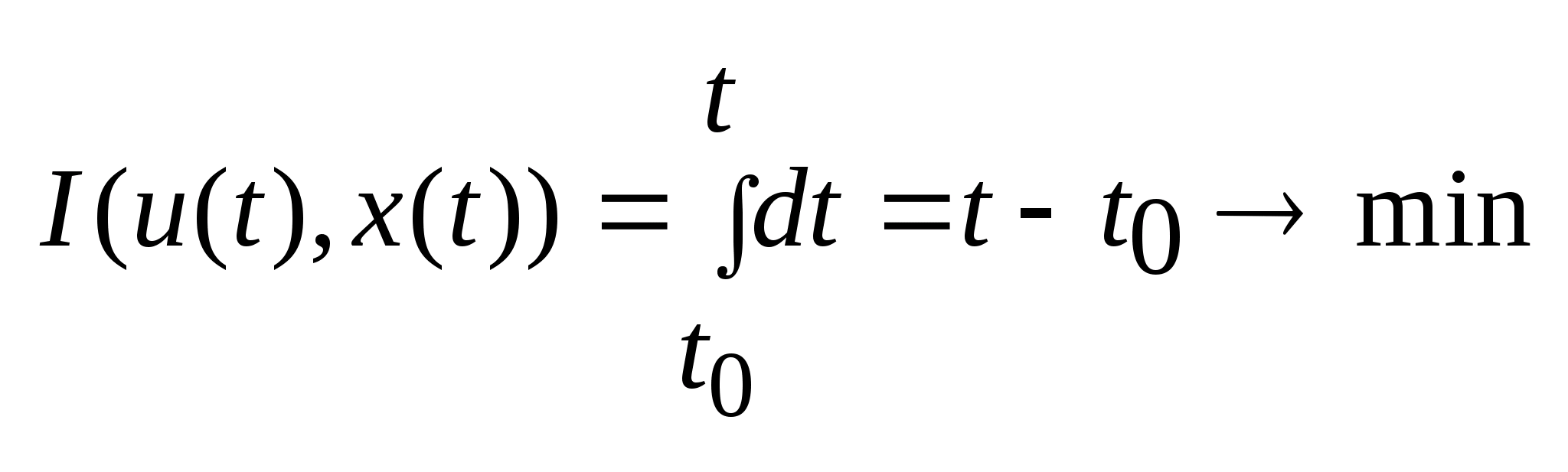 (4).
(4).
Рассмотрим
систему линейных дифференциальных
уравнений:
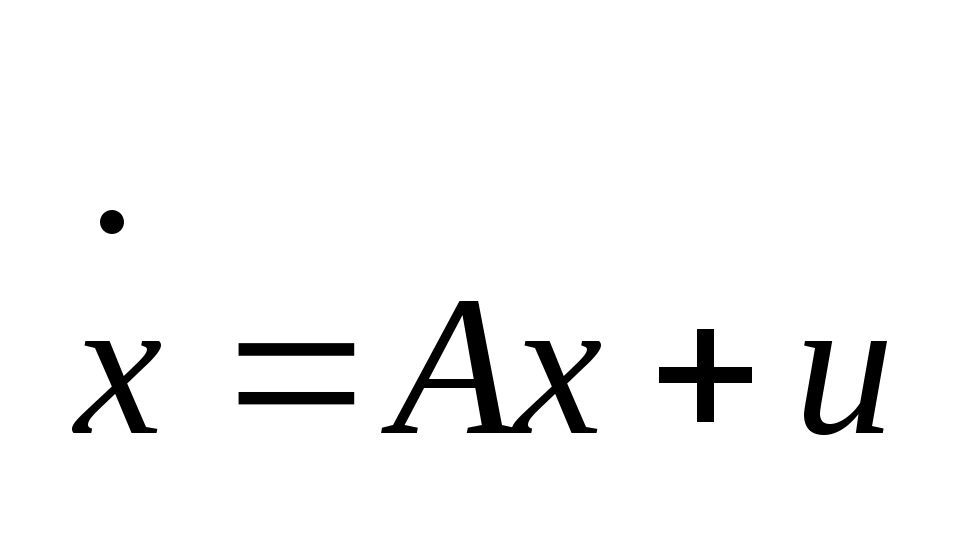 ,
,
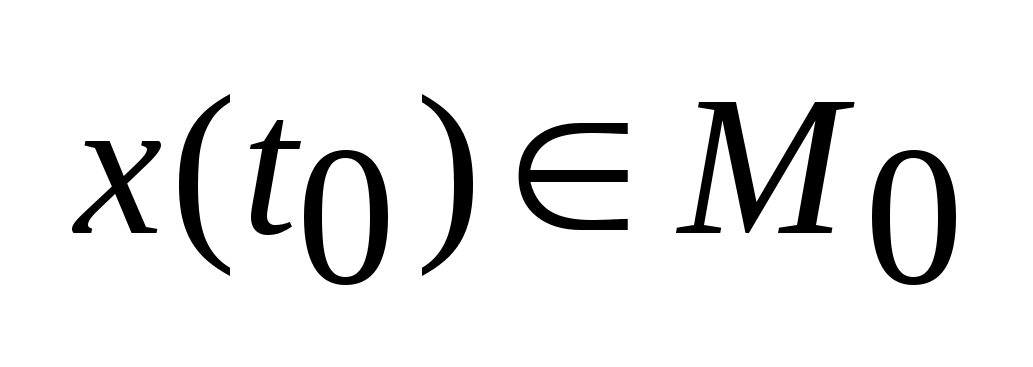 ,
где u
известное . Решение задачи Коши
записывается в виде:
,
где u
известное . Решение задачи Коши
записывается в виде:
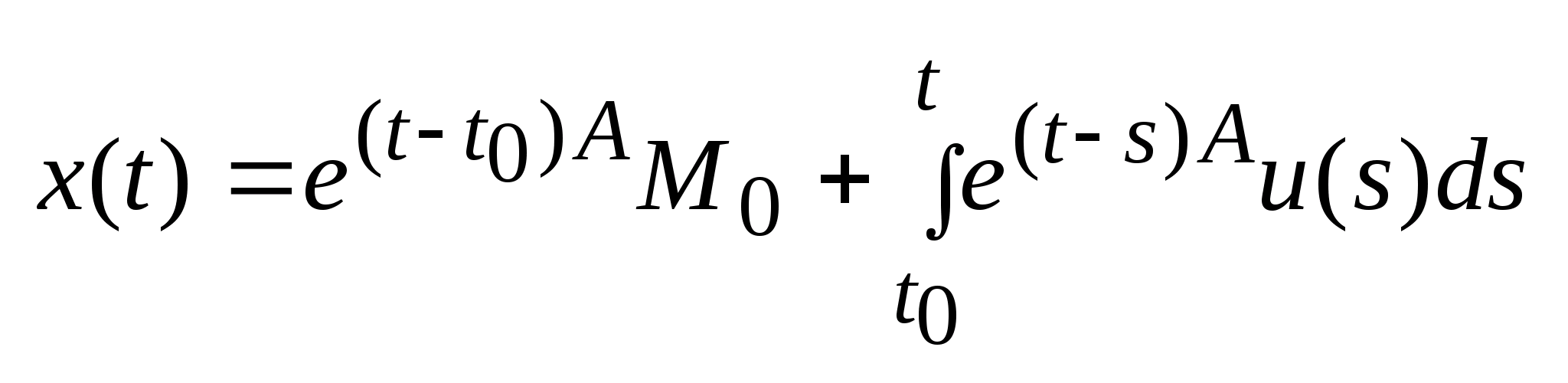 ,
оно справедливо, если u-
непрерывная.
,
оно справедливо, если u-
непрерывная.
Вычислим
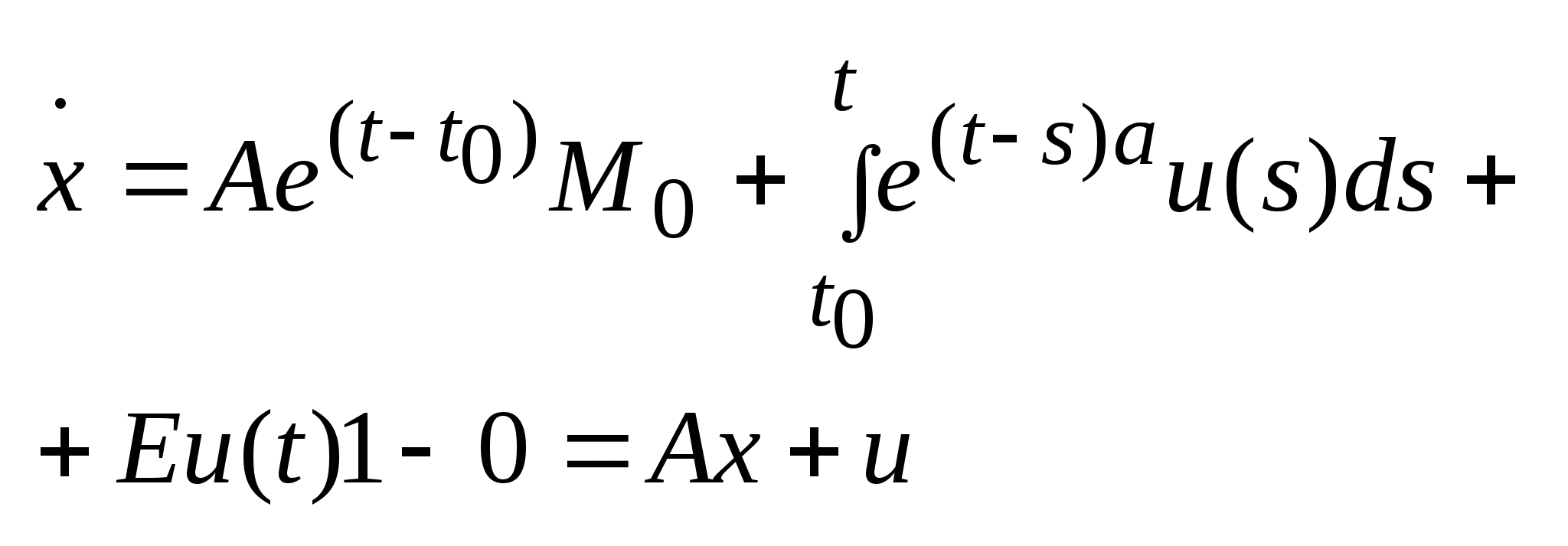 (это
следует из
(это
следует из

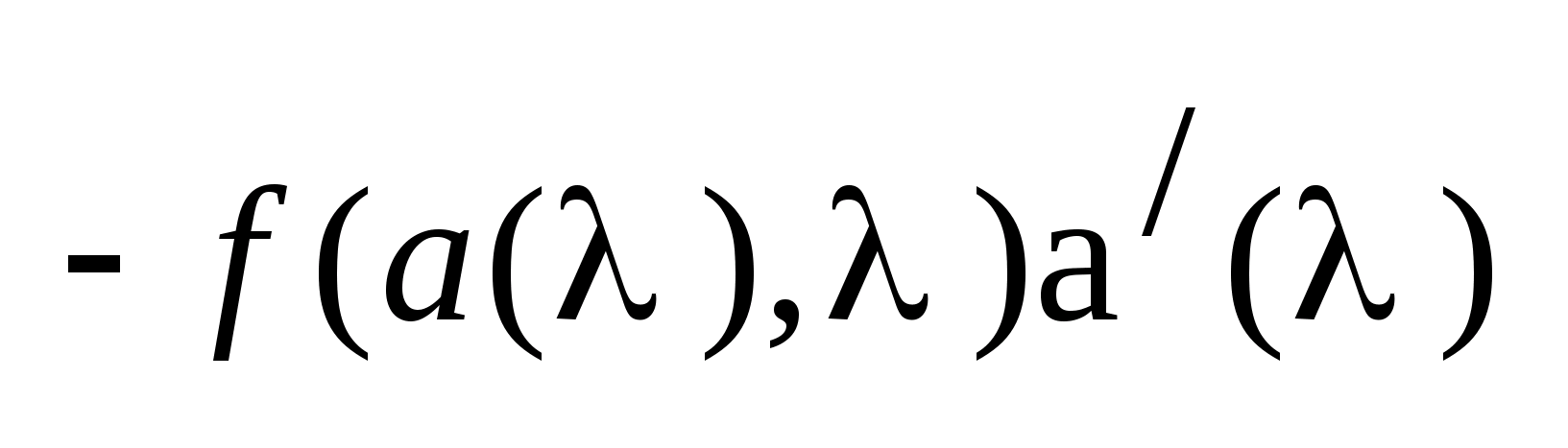 ).
).
Определение:
Функцию x(t)
наз. абсолютно непрерывной на отр. I,
если ее производная существует для
почти всех t,
принадлежащих I, интегрируемая по Лебегу
производная
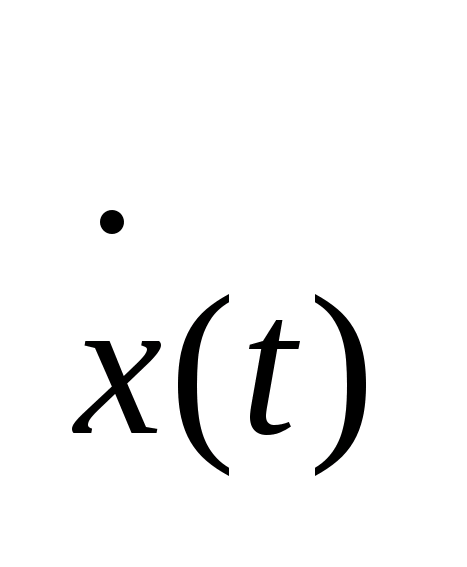 и
выполняется условие:
и
выполняется условие:
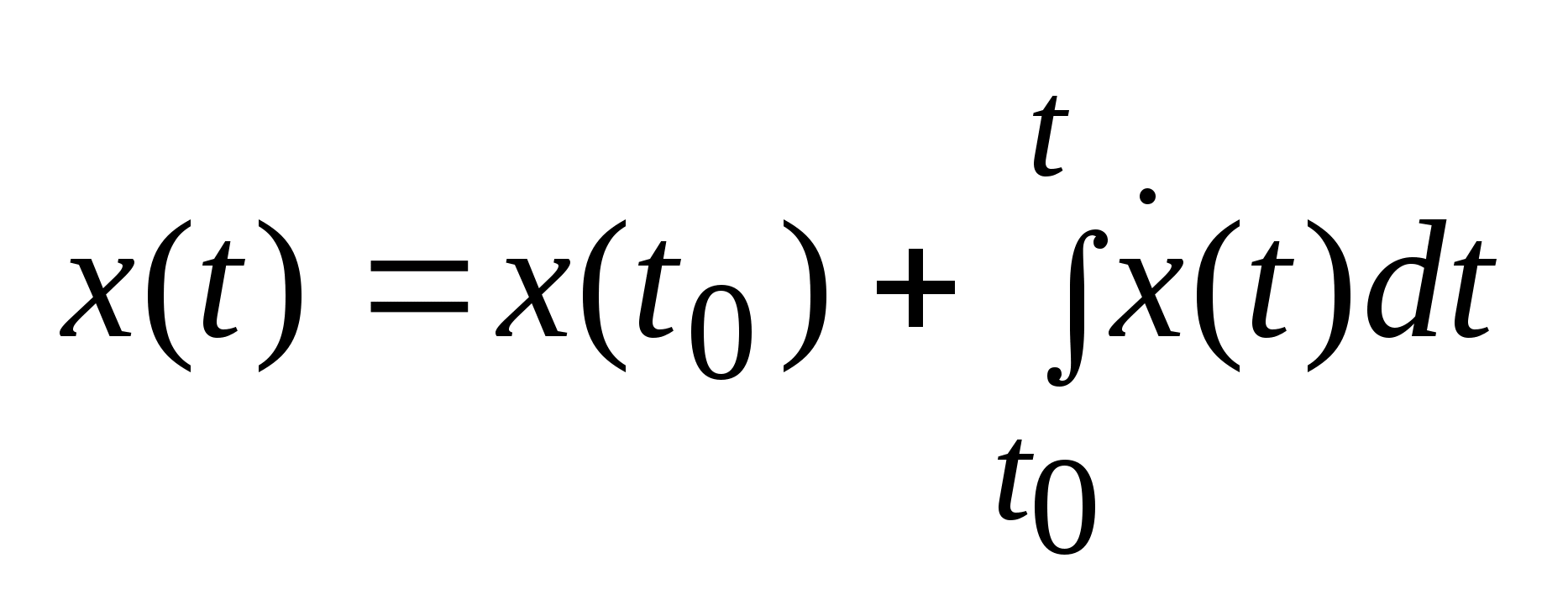 .
.
Если имеем измеримое допустимое управление u(t), то решение системы (1) также можно определить с помощью формулы Коши, но в этом случае x(t) не будет непрерывно дифференцируема, а будет абсолютно непрерывной.
Теорема
Каратеородори:
Если функция u(t)
интегрируемая по Лебегу на отр. I,
то для любого начального значения
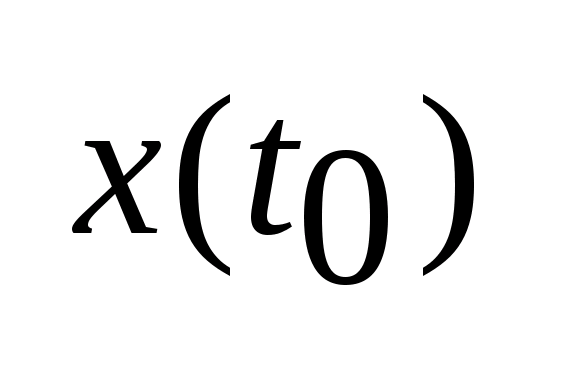 существует
и при том единое абс. непрерывное решение
задачи Коши, которая задается
формулой
Коши.
существует
и при том единое абс. непрерывное решение
задачи Коши, которая задается
формулой
Коши.
15. Множество достижимости и его свойства.
Рассматриваем
динамический объект, поведение которого
описывается системой (1)
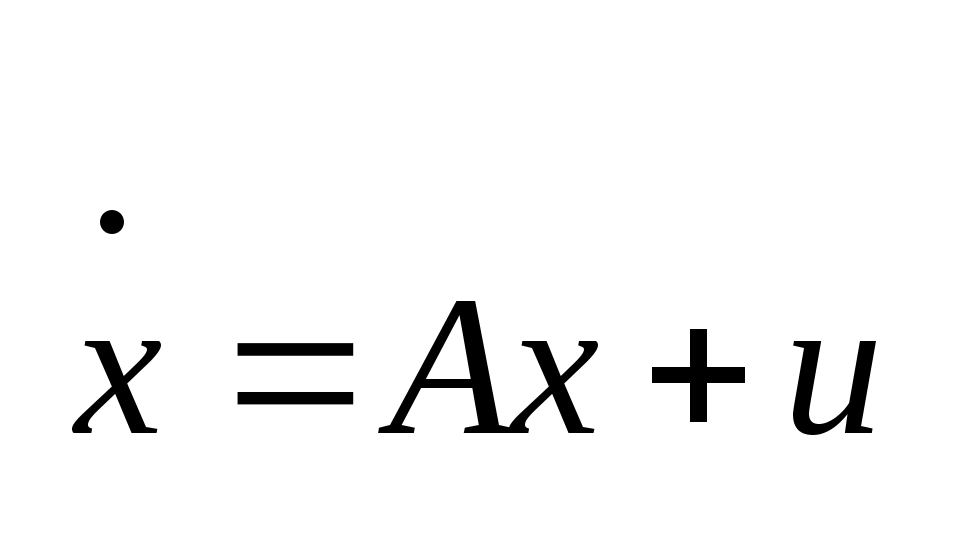 ,
x-
n-мерный
вектор,
,
x-
n-мерный
вектор,
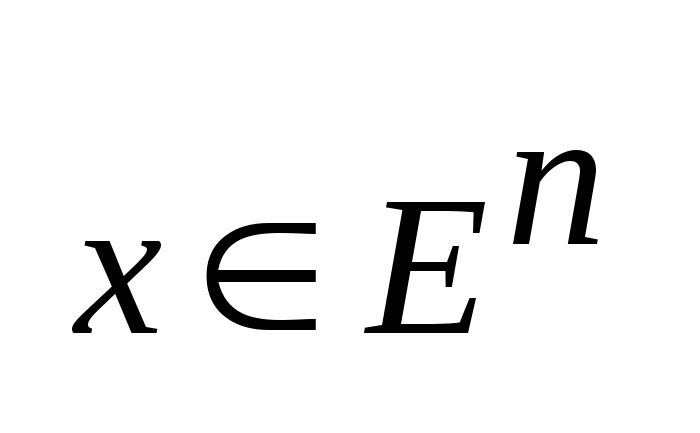 ,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
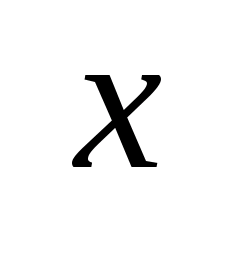 ,
,
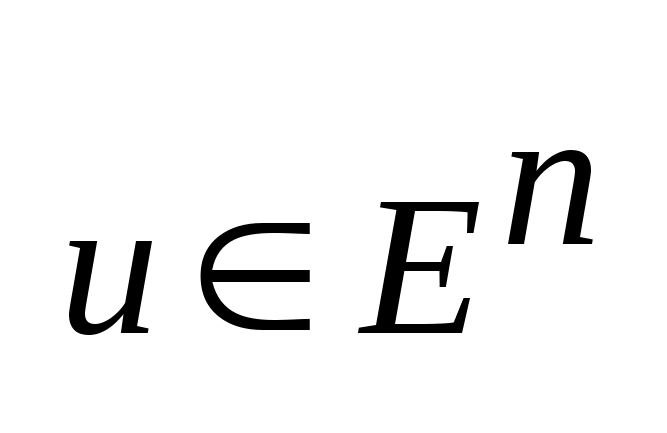 .Задано
.Задано
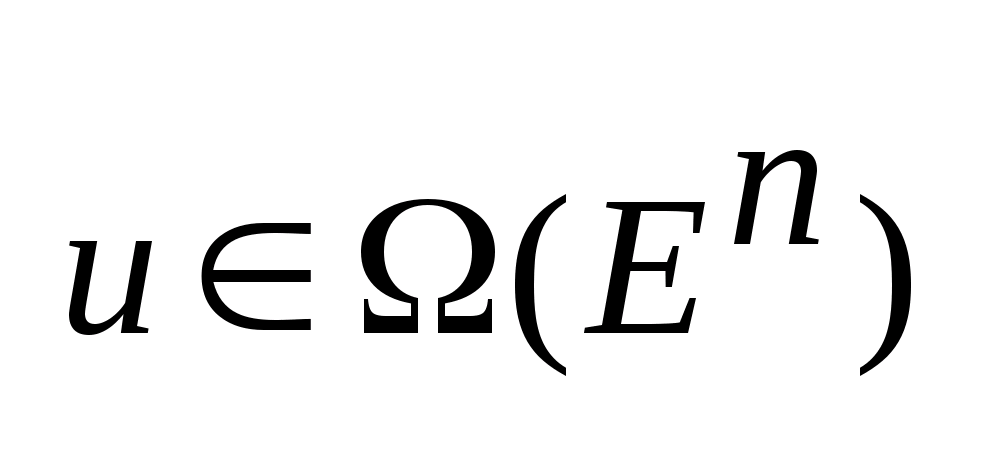 ,
u:
I
,
u:
I
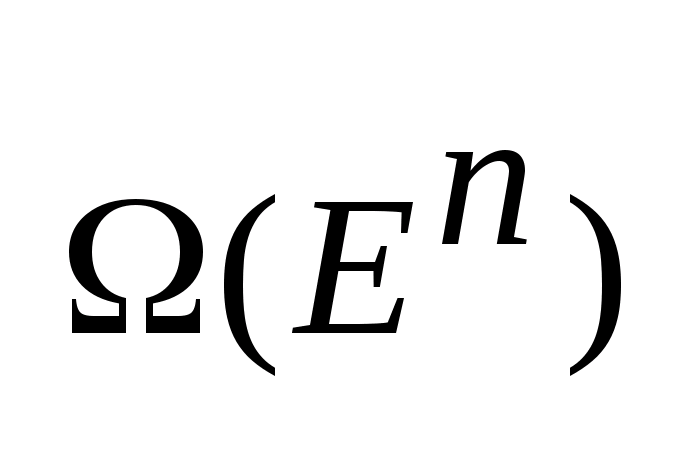 и полагается, что u(t)
измеримо
и
и полагается, что u(t)
измеримо
и
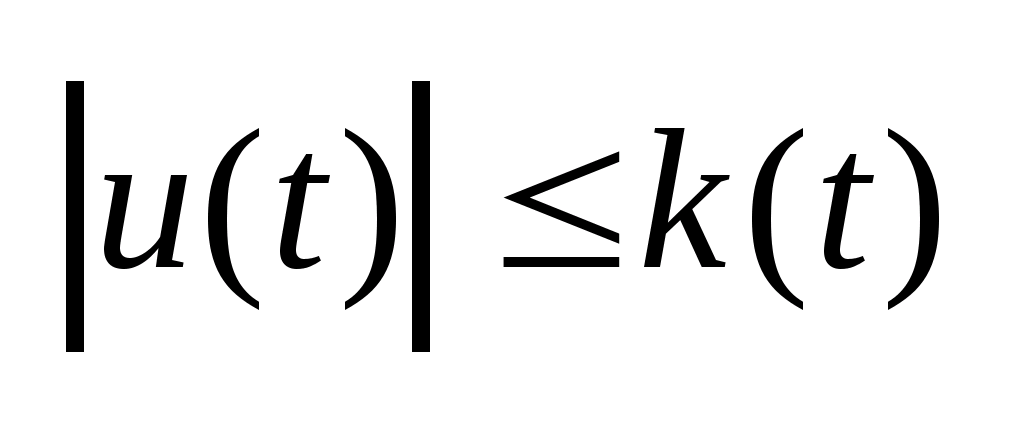 -
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью (2) u(t)
-
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью (2) u(t)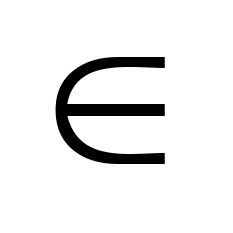 U(t)-
ограничения на управления . В фазовом
пространстве
U(t)-
ограничения на управления . В фазовом
пространстве
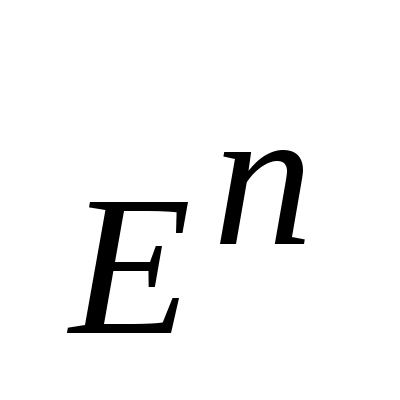 заданы
два не пустых множества
заданы
два не пустых множества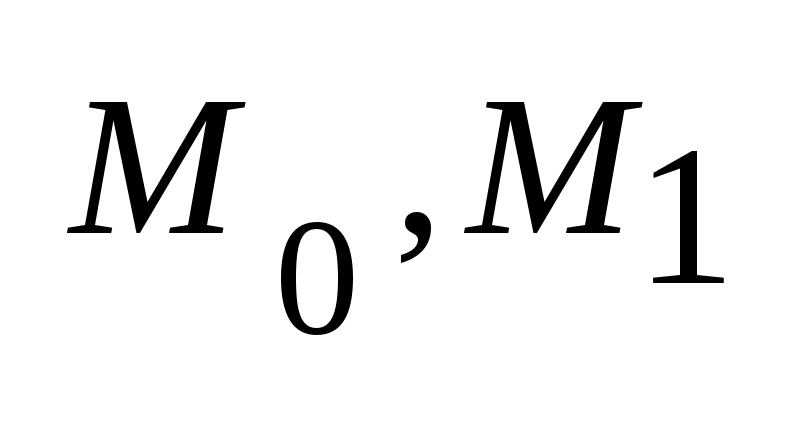
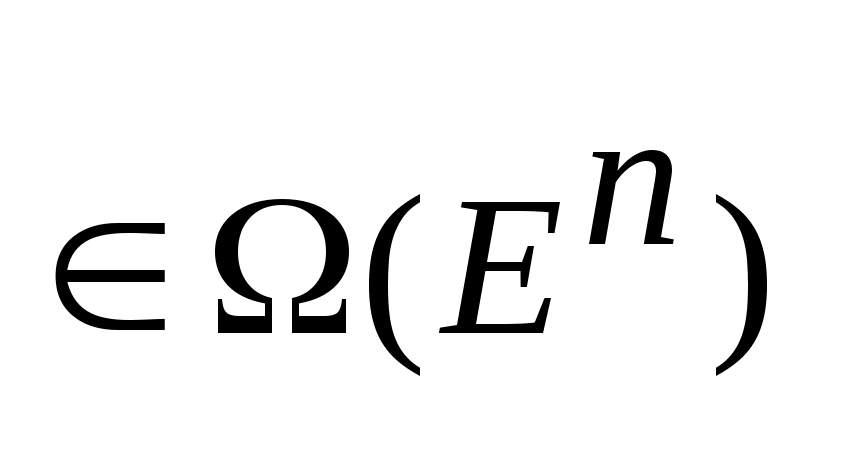 .
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
 в конечное множество
в конечное множество
 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
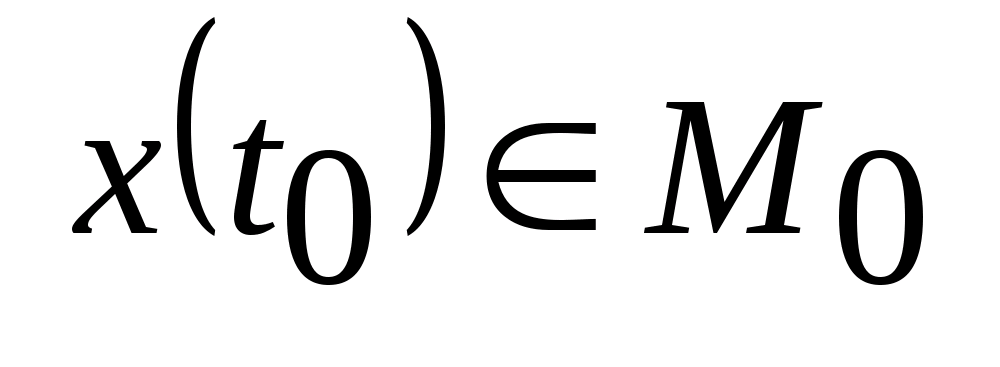 и
и
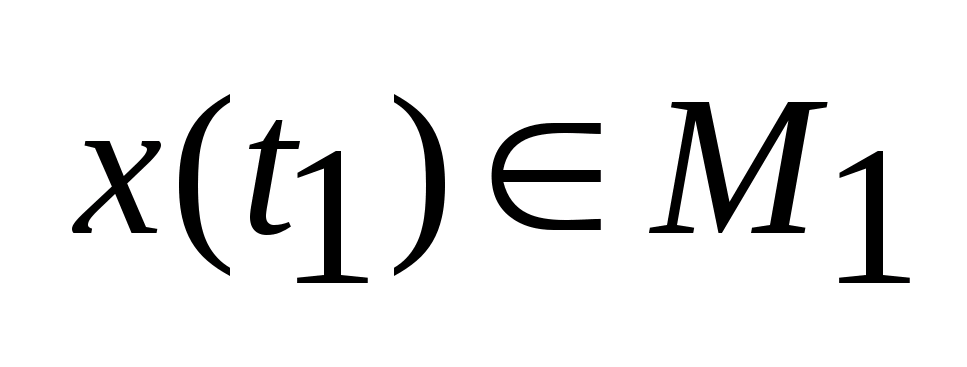 .
Цель управления- перевод динамический
объекта из
.
Цель управления- перевод динамический
объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача
быстродействия заключается в нахождении
такого допустимого управления, которое
осуществляет переход из множества
 в
в
 за
наименьшее время.
за
наименьшее время.
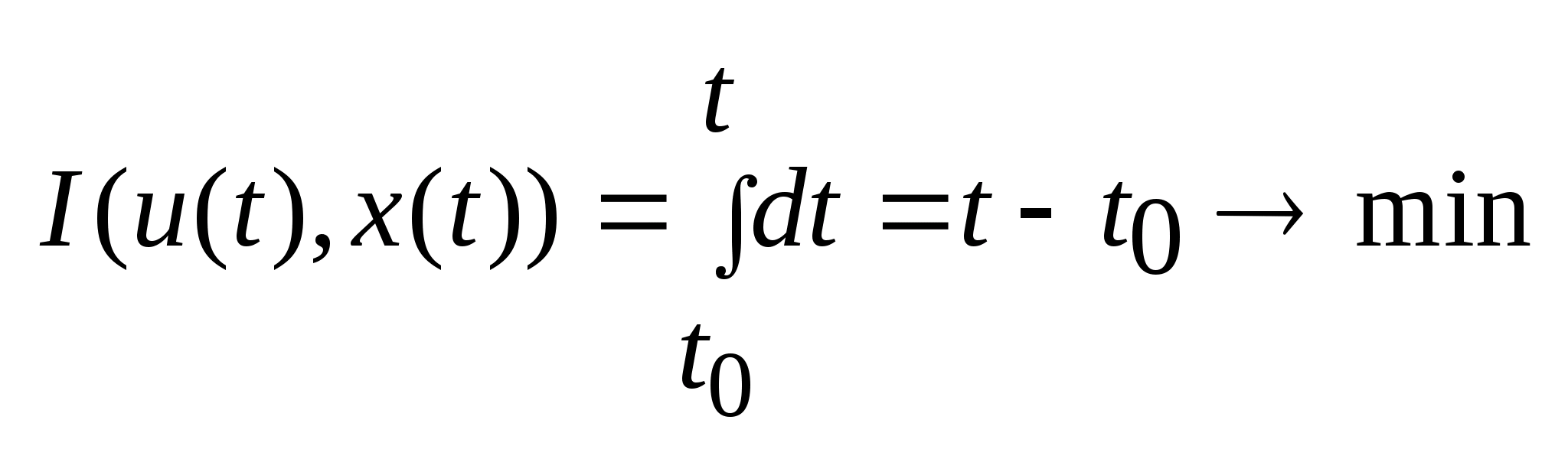 (4).
(4).
Введем
понятия мн-ва достижимости:
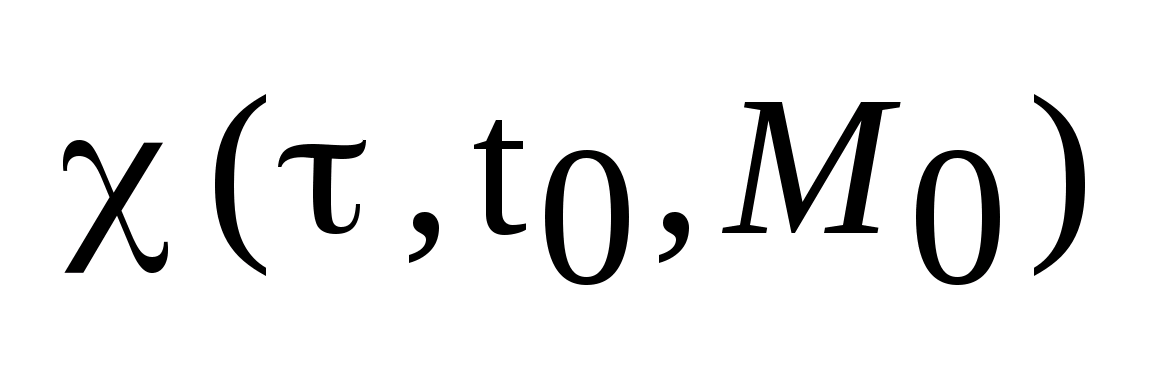 -это
множество все точек фазового пространства
-это
множество все точек фазового пространства
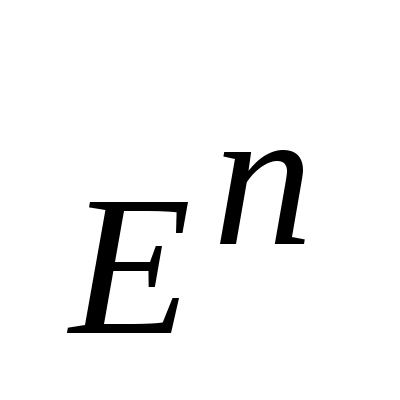 ,
в котором можно перейти на отр.
,
в котором можно перейти на отр.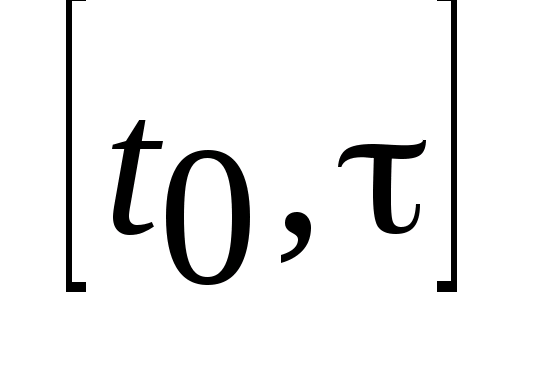 из начального множества
из начального множества
 по
решениям (1) при всех допустимых значениях
управления u(t)
в
момент времени
по
решениям (1) при всех допустимых значениях
управления u(t)
в
момент времени
 .
.
Рассмотрим свойства множества достижимости:
1)
Используем
формулу Коши: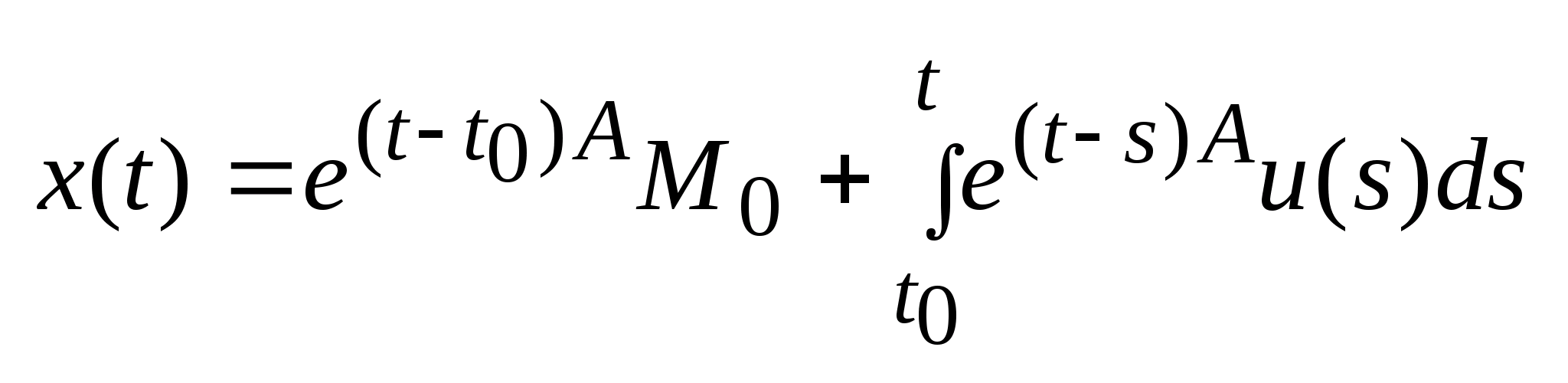
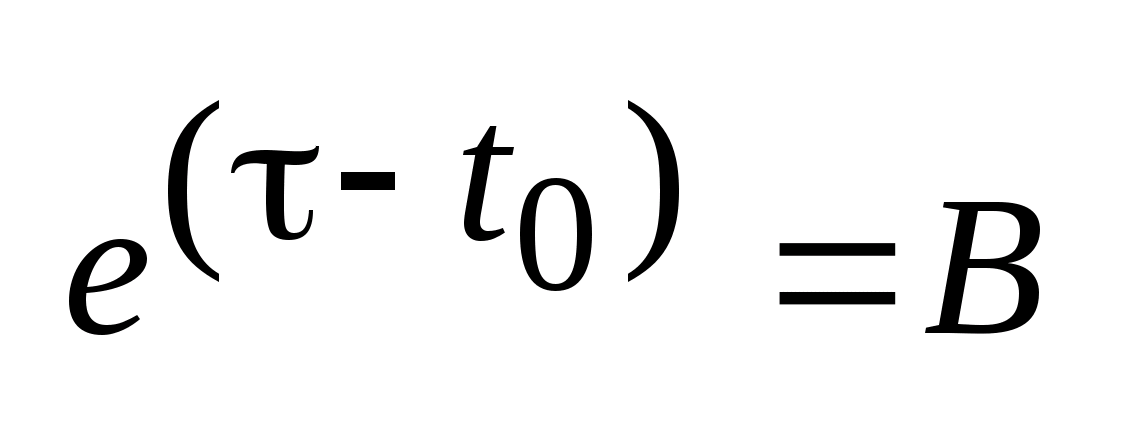 ,
,
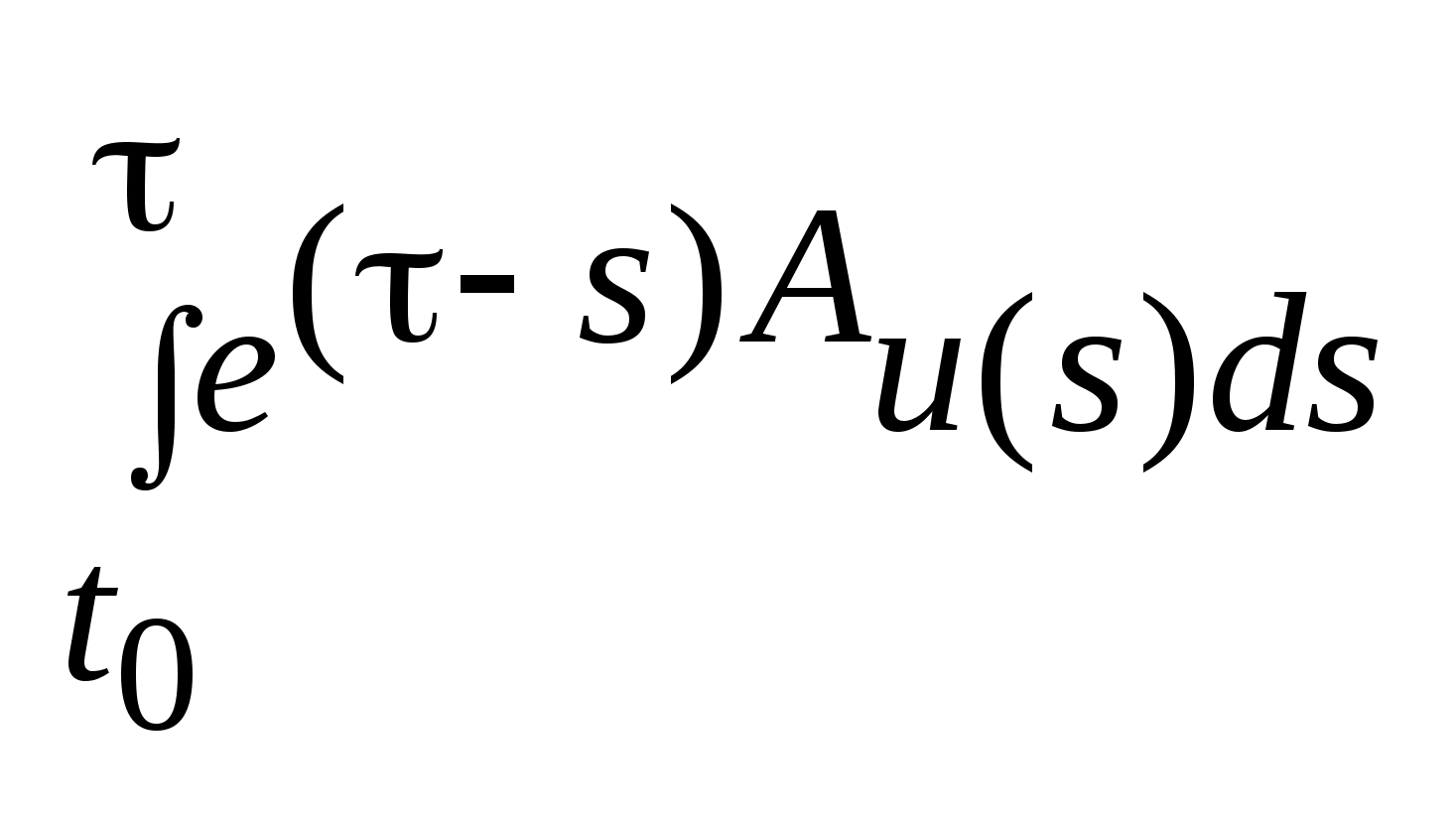 -интеграл
от многозначного отображения.
Доказательство непосредственно
подставлением
в
уравн (1).
-интеграл
от многозначного отображения.
Доказательство непосредственно
подставлением
в
уравн (1).
2)
Множество
достижимости является не пустым,
компактным подмножеством пр-ва
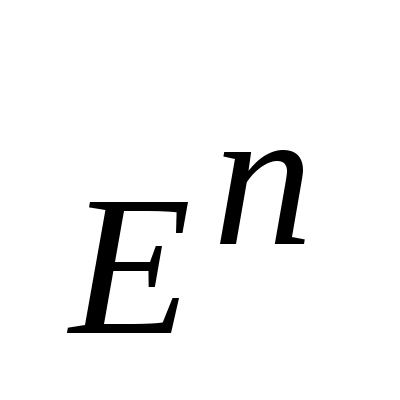 .
.
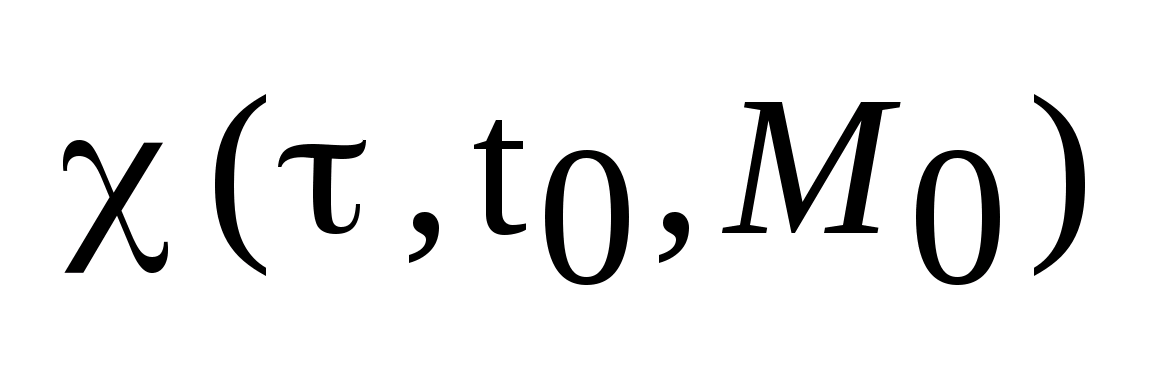
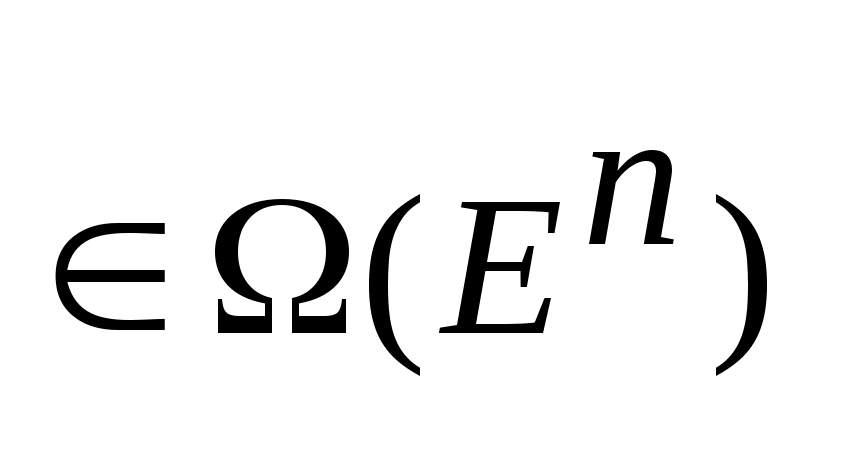 .
.
Доказательство следует из формулы Коши и 1-ой теоремы для интеграла многозначных отображений.
3)
Если начальное множество
 выпукло,
то множество достижимости
выпукло,
то множество достижимости
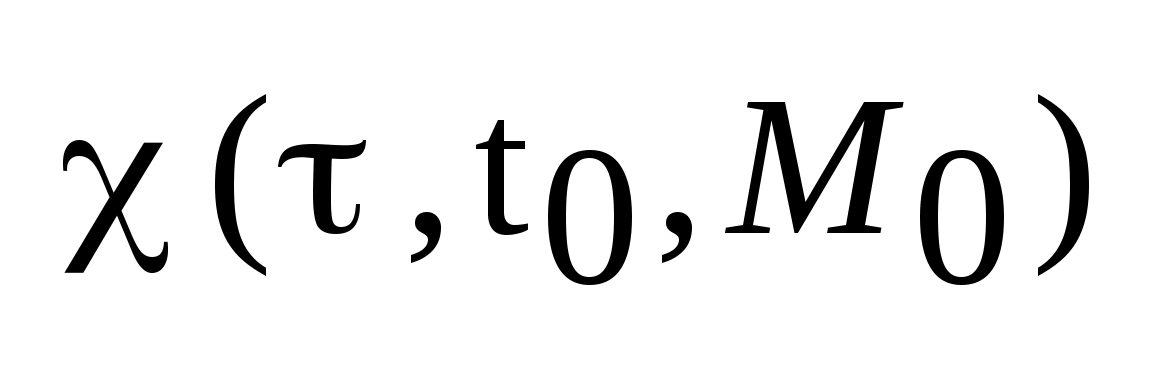 также
выпукло. Доказательство следует из
формулы
также
выпукло. Доказательство следует из
формулы
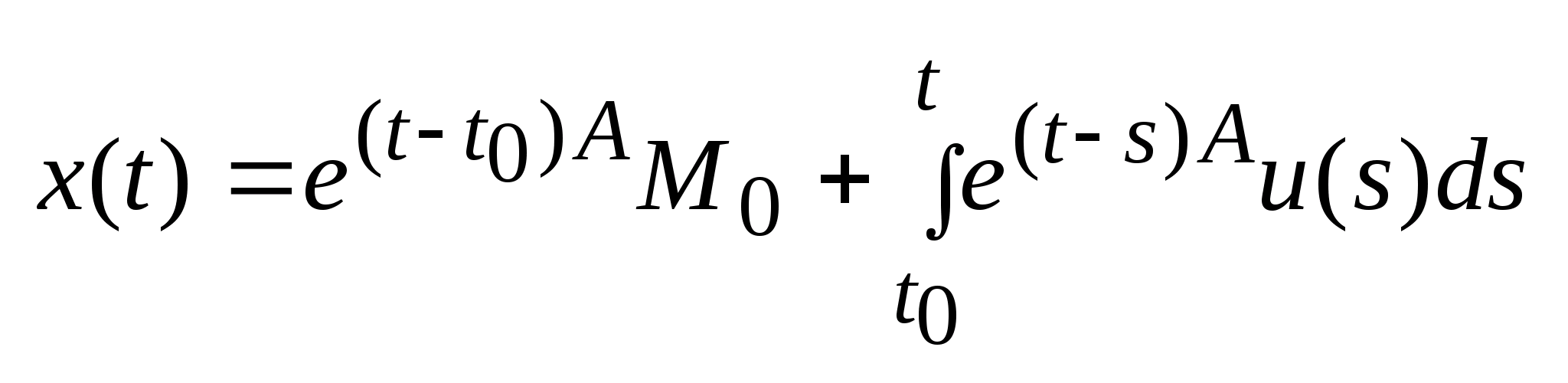 и теоремы о выпуклости интеграла от
многозначного отображения.
и теоремы о выпуклости интеграла от
многозначного отображения.
4)
Опорная функция множества достижимости
имеет вид:
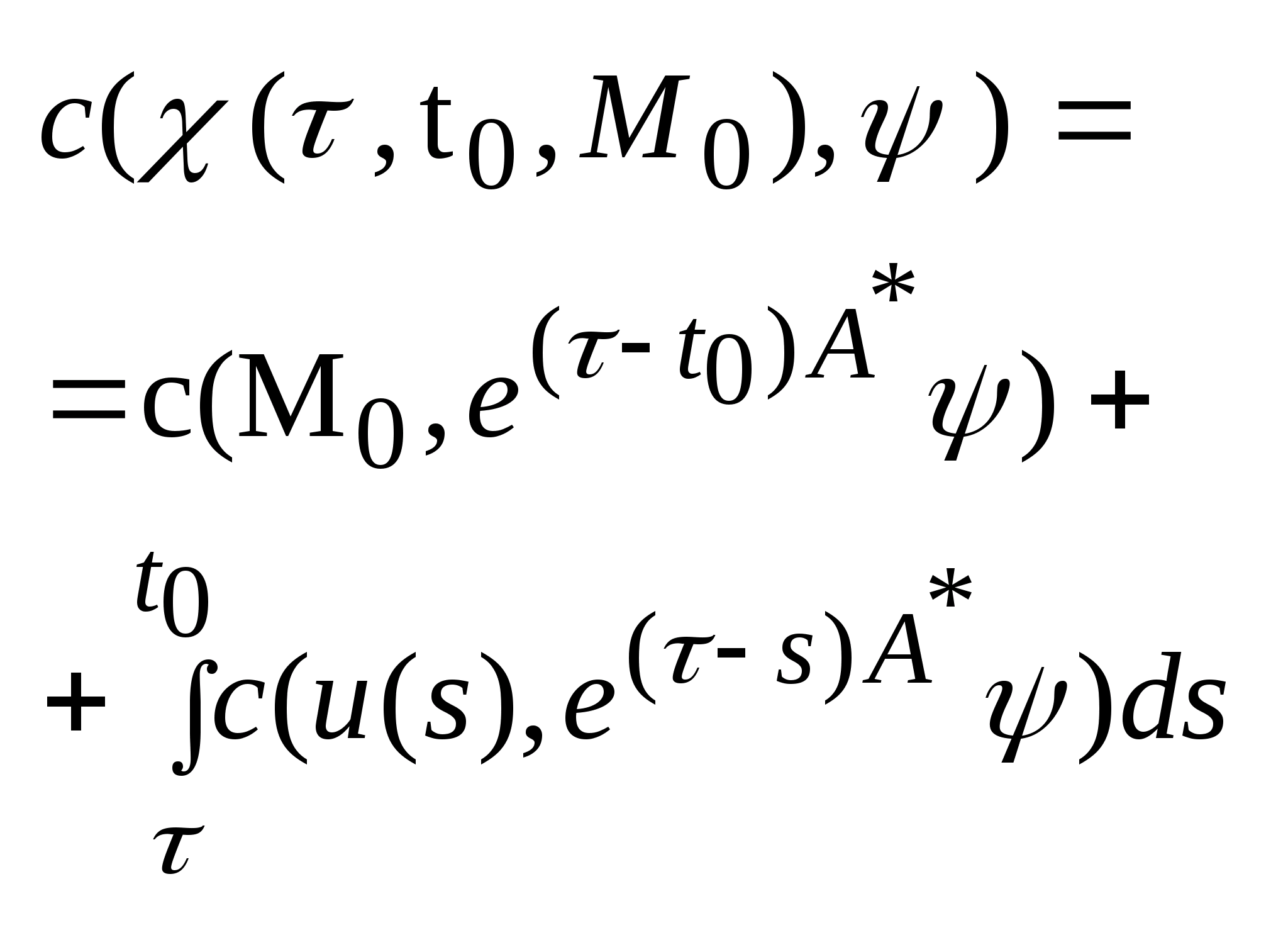 ,
u(s)=U. Доказательство
следует из формулы
,
u(s)=U. Доказательство
следует из формулы
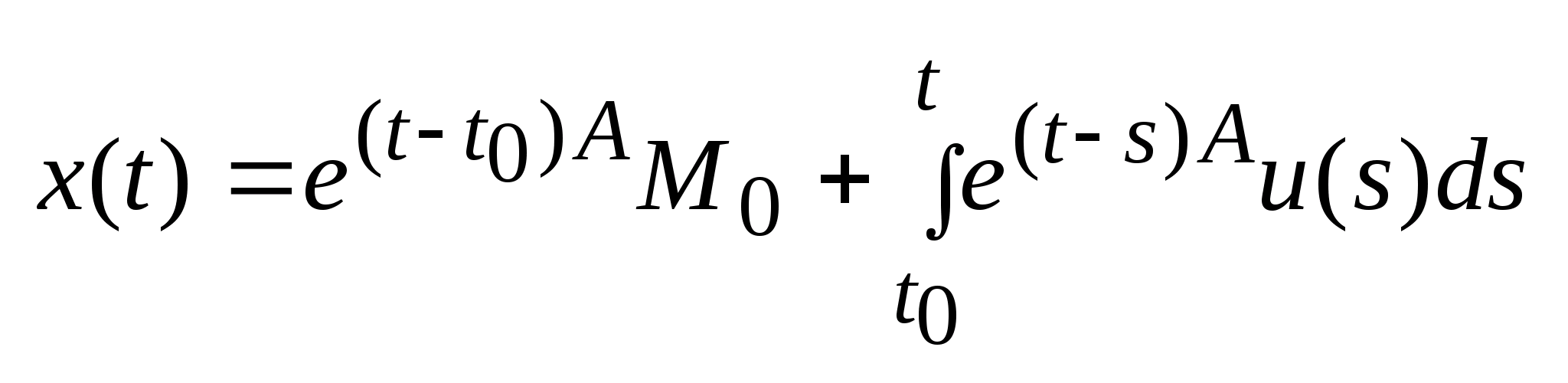 ,
свойств (3), (4) опорных функций , теоремы
2 и того факта, что
,
свойств (3), (4) опорных функций , теоремы
2 и того факта, что
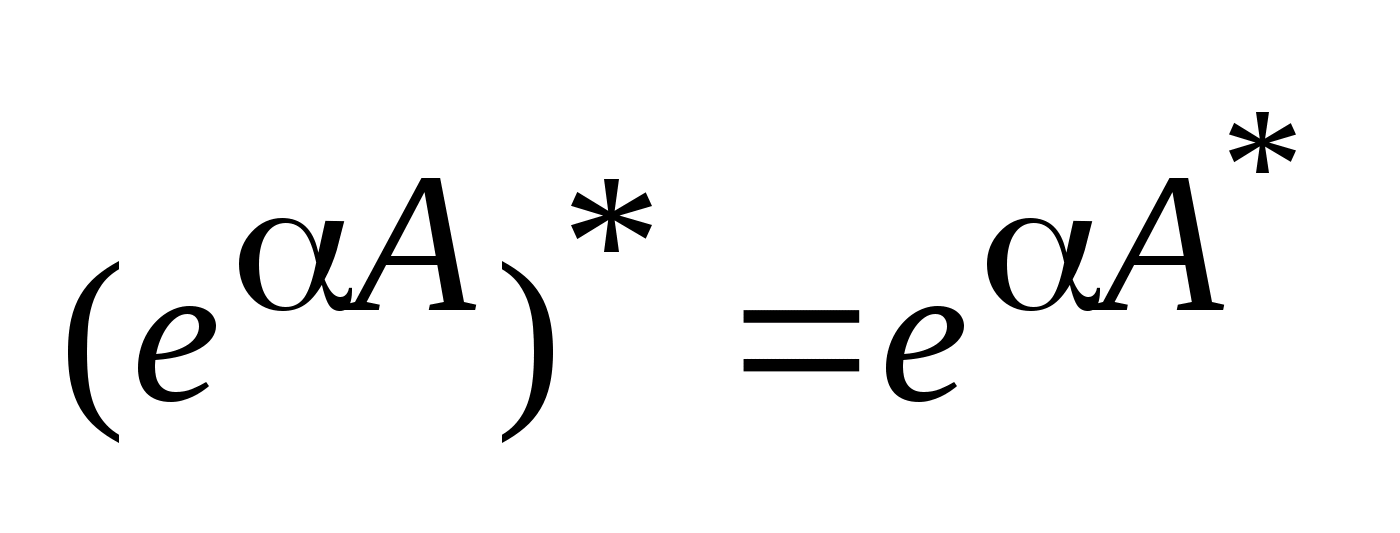 .
.
Доказательство:
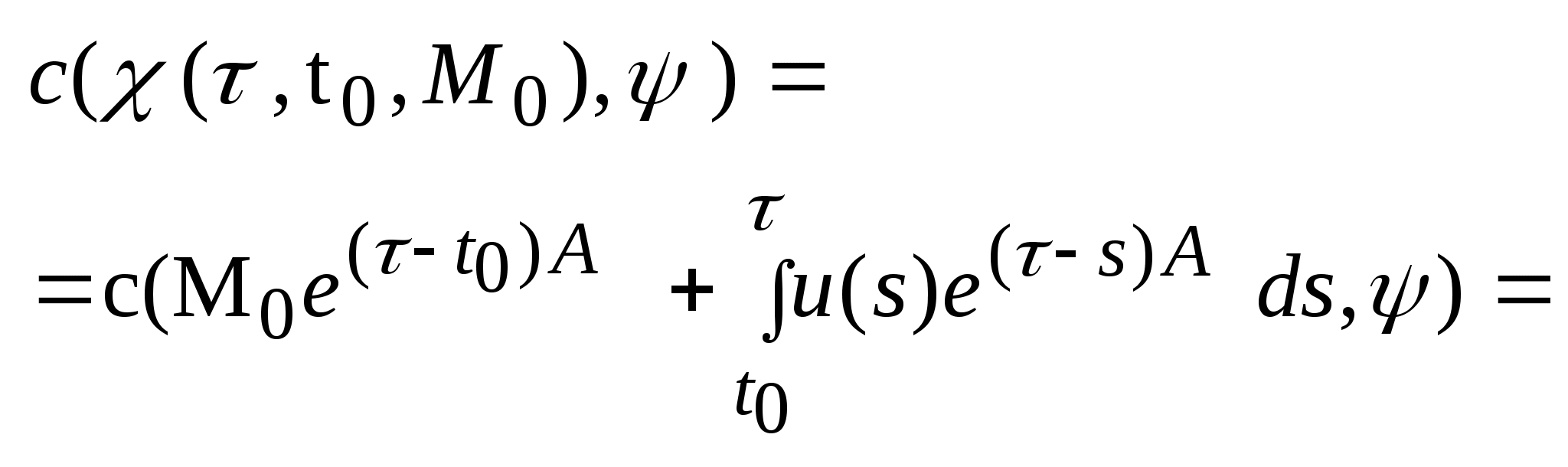
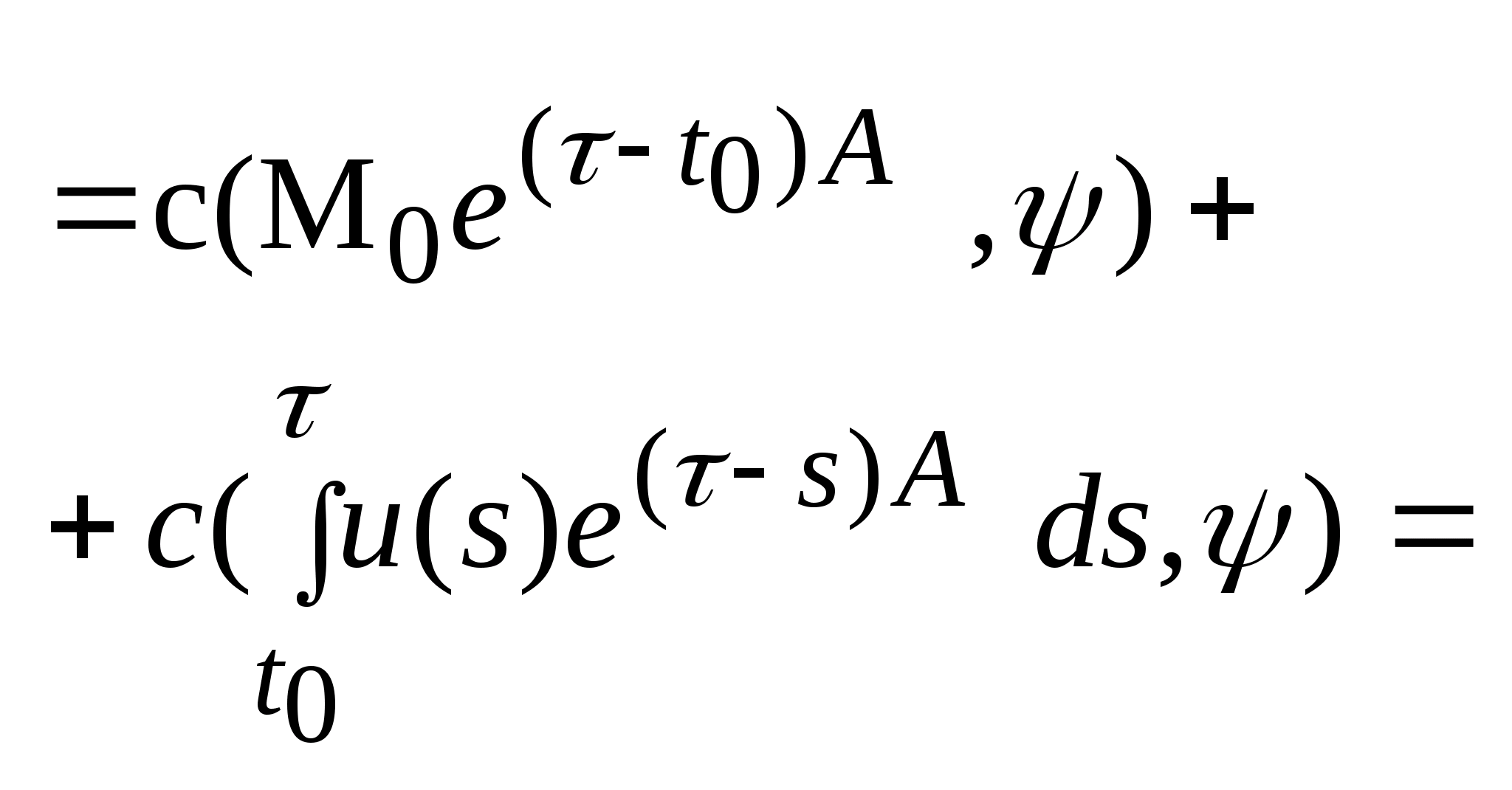
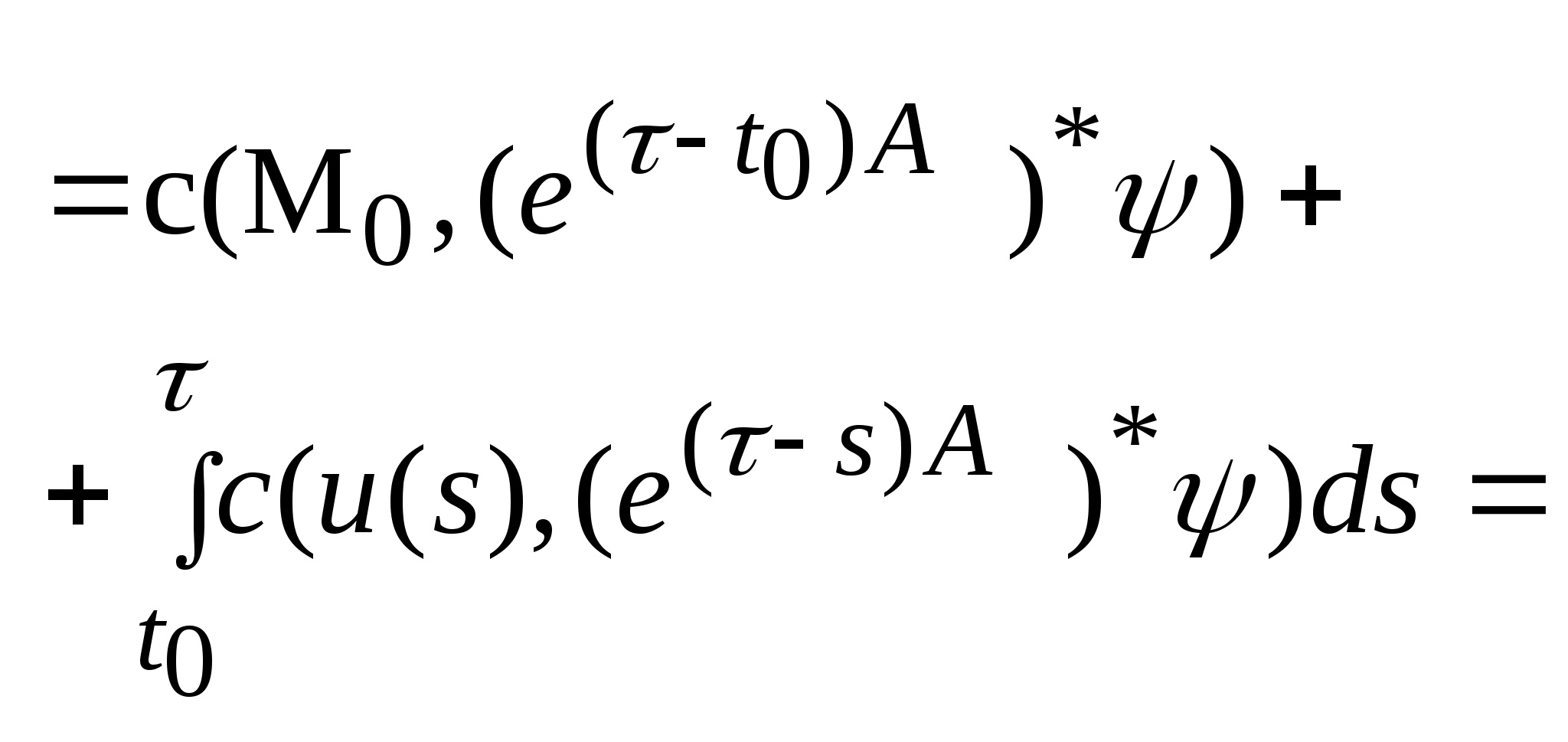
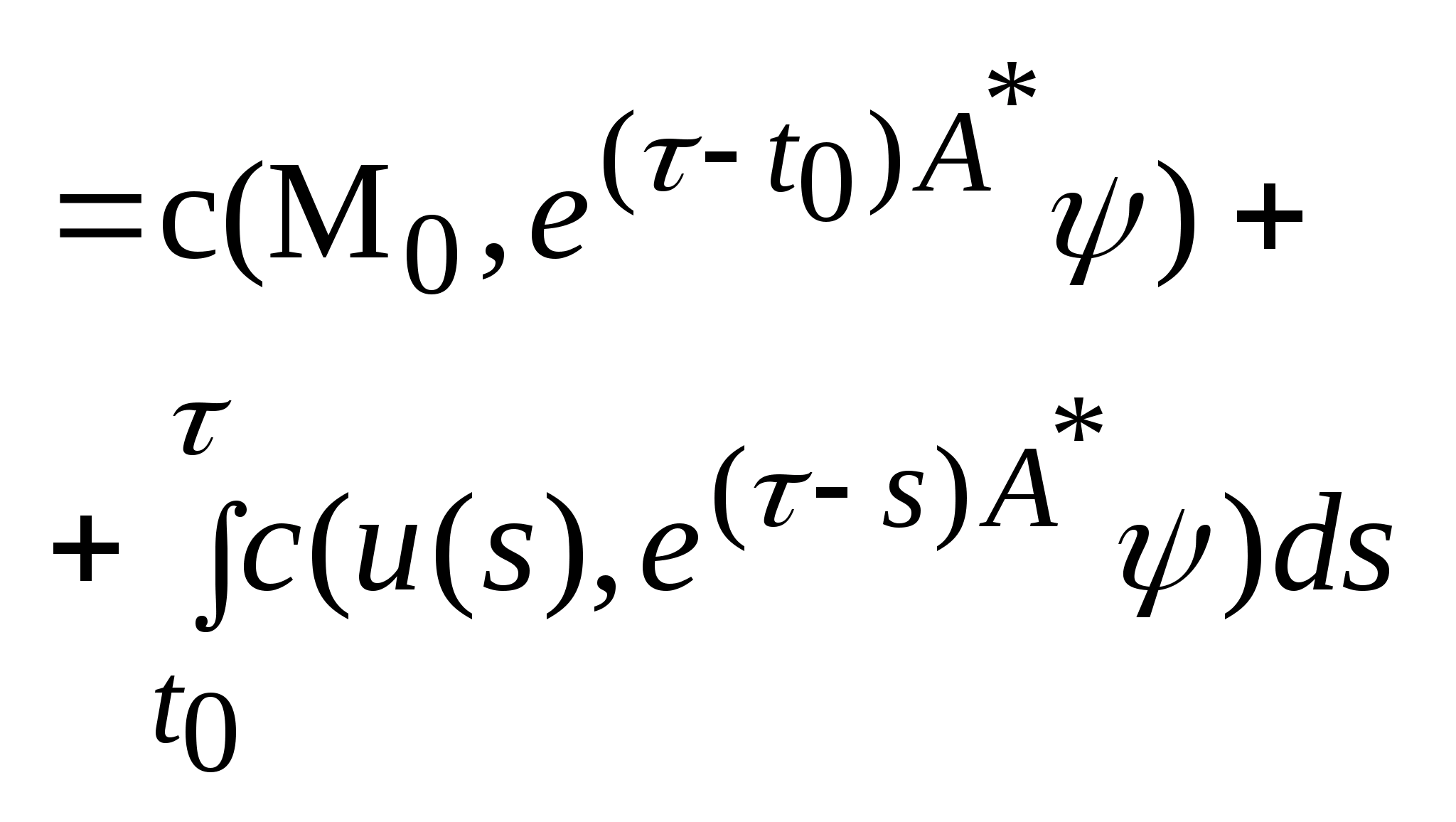 .
.
5)
Мн-во
достижимости:
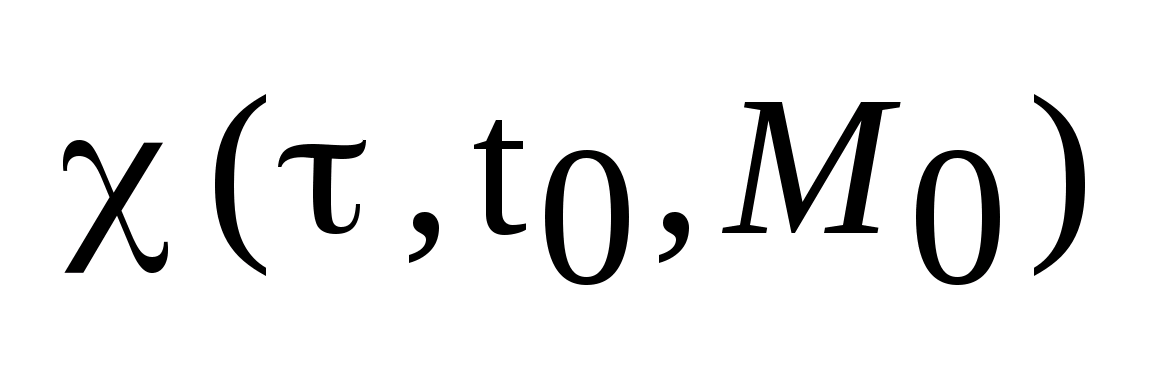 :
I
:
I
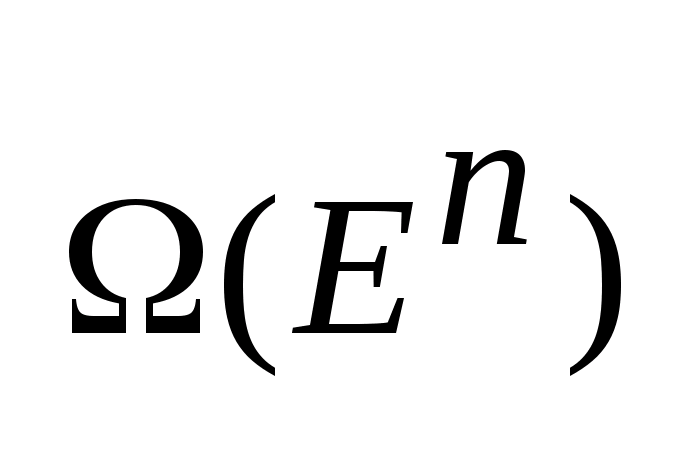 непрерывно
зависит от аргумента
непрерывно
зависит от аргумента
 .
Множество достижимости имеет вид :
.
Множество достижимости имеет вид :
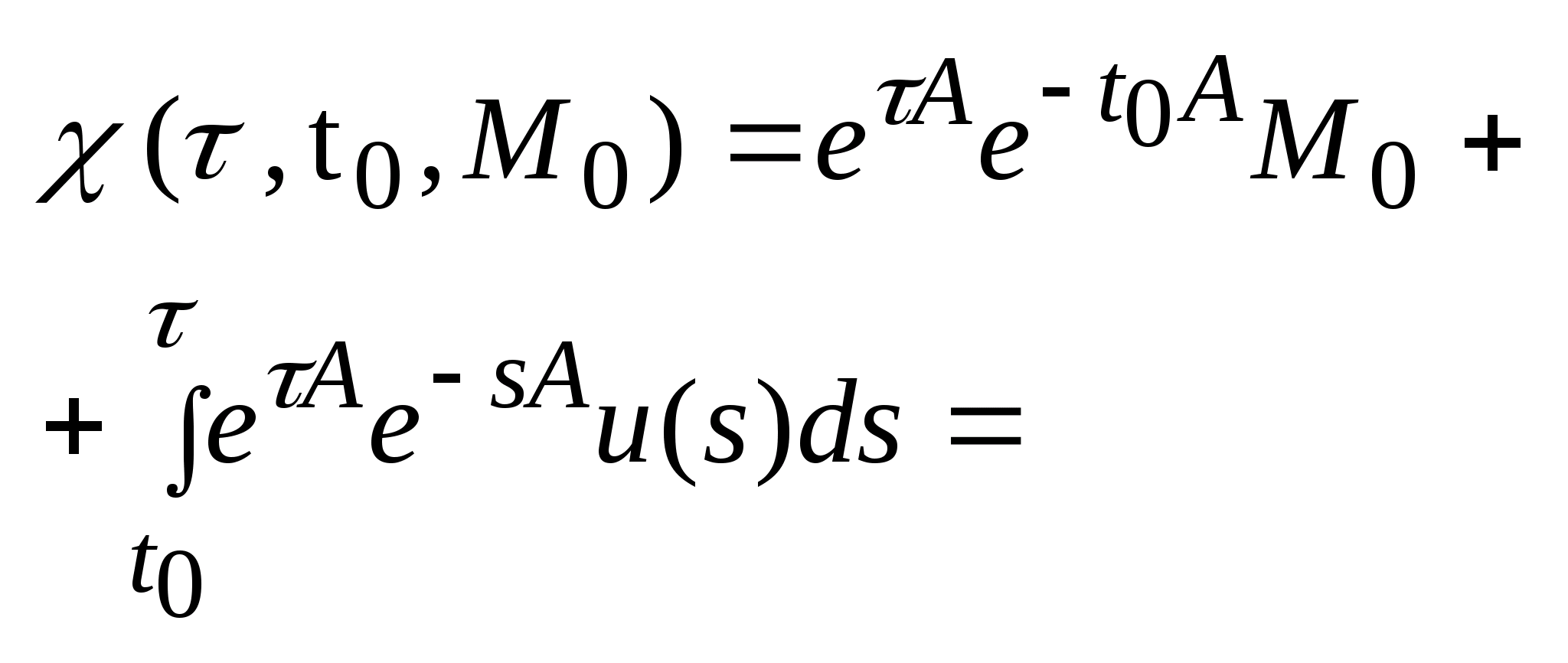
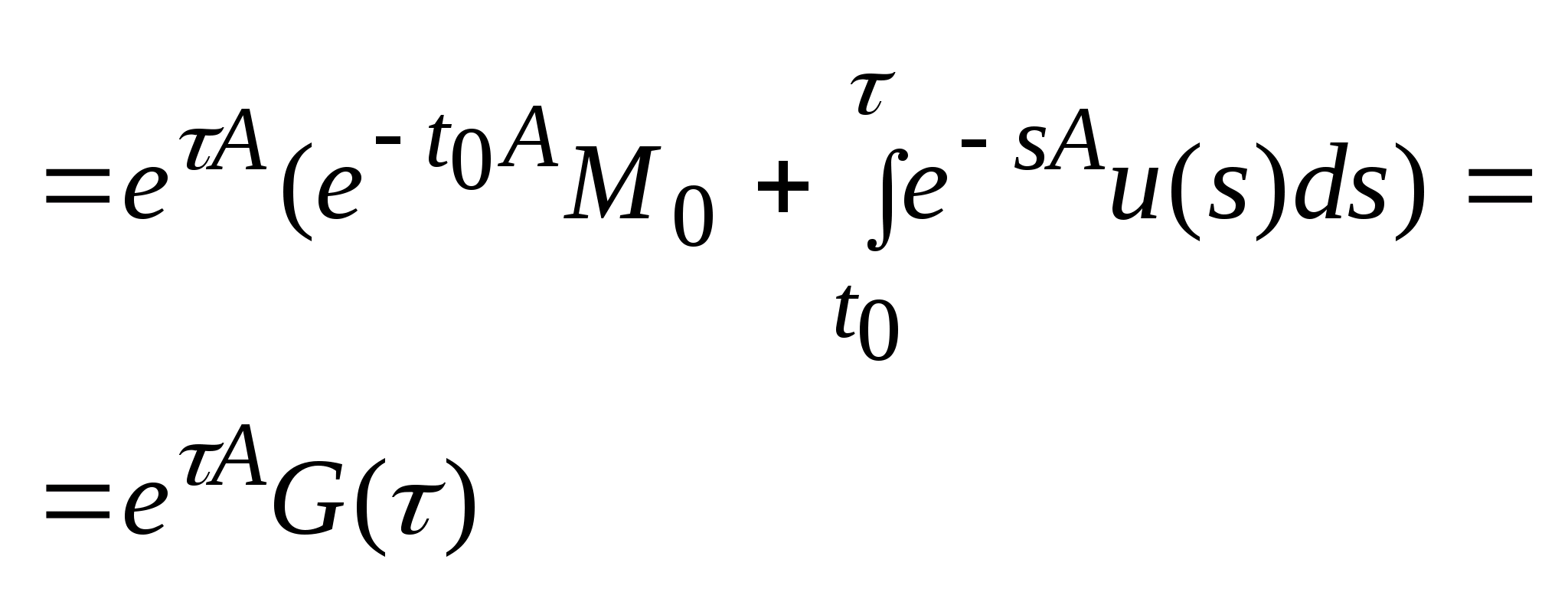
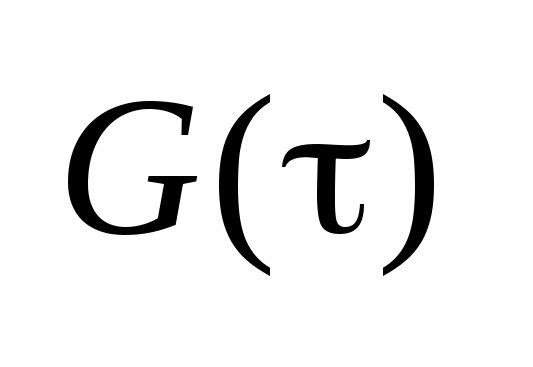 -непрерывна
по теореме 3, матрица
-непрерывна
по теореме 3, матрица
 также
непрерывна по
также
непрерывна по
 ,
следовательно линейное отображение
непрерывная функция.
,
следовательно линейное отображение
непрерывная функция.
Пример:
Найти мн-во достижимости для управляемого
объекта, описываемого уравнением: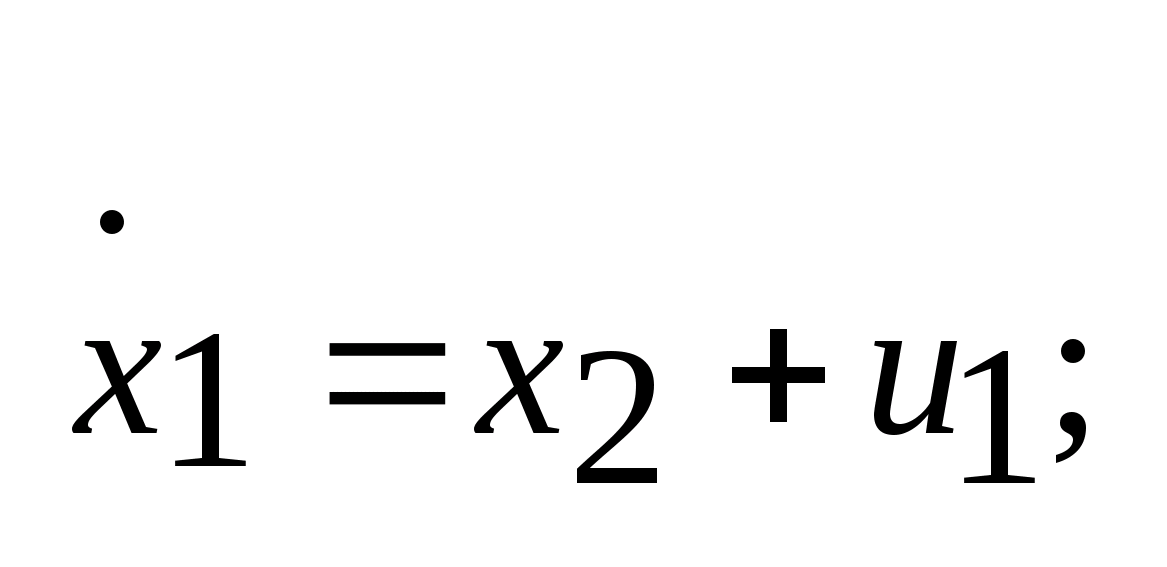
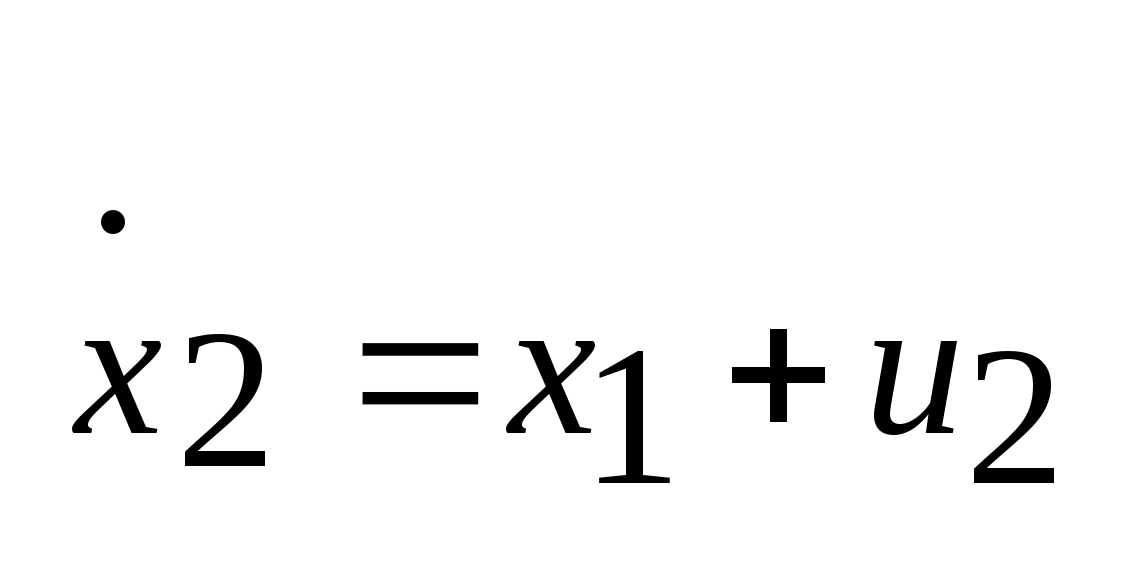 .
.
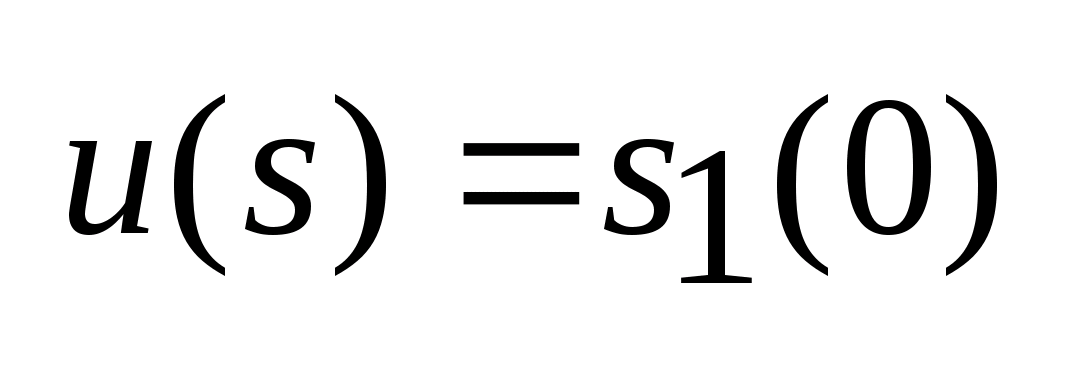 ,
,
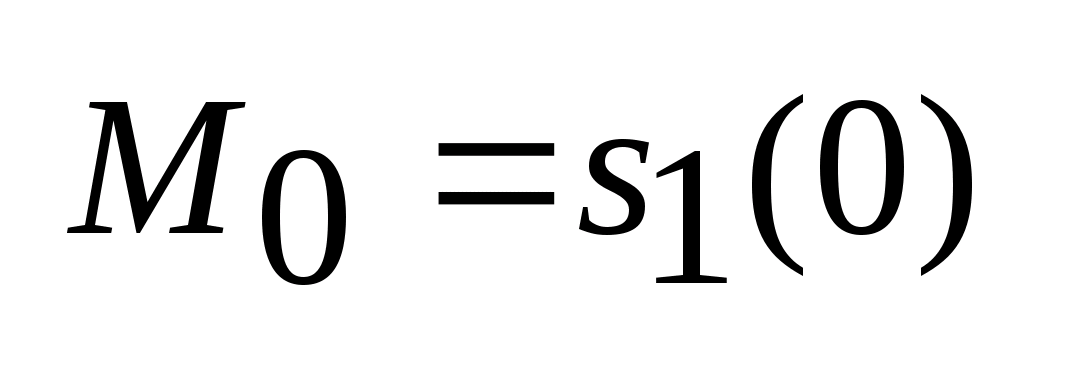 и
и
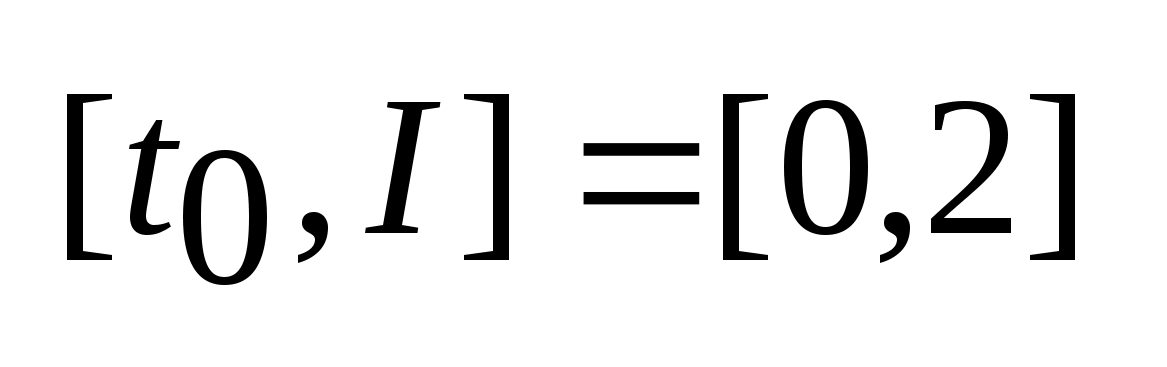 ,
I
,
I
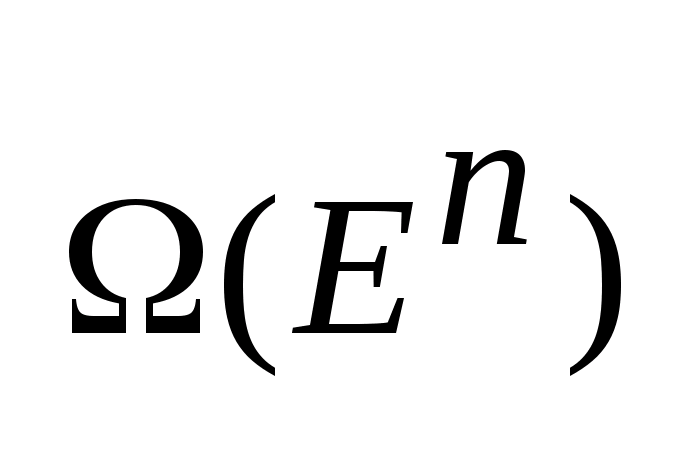 .
.
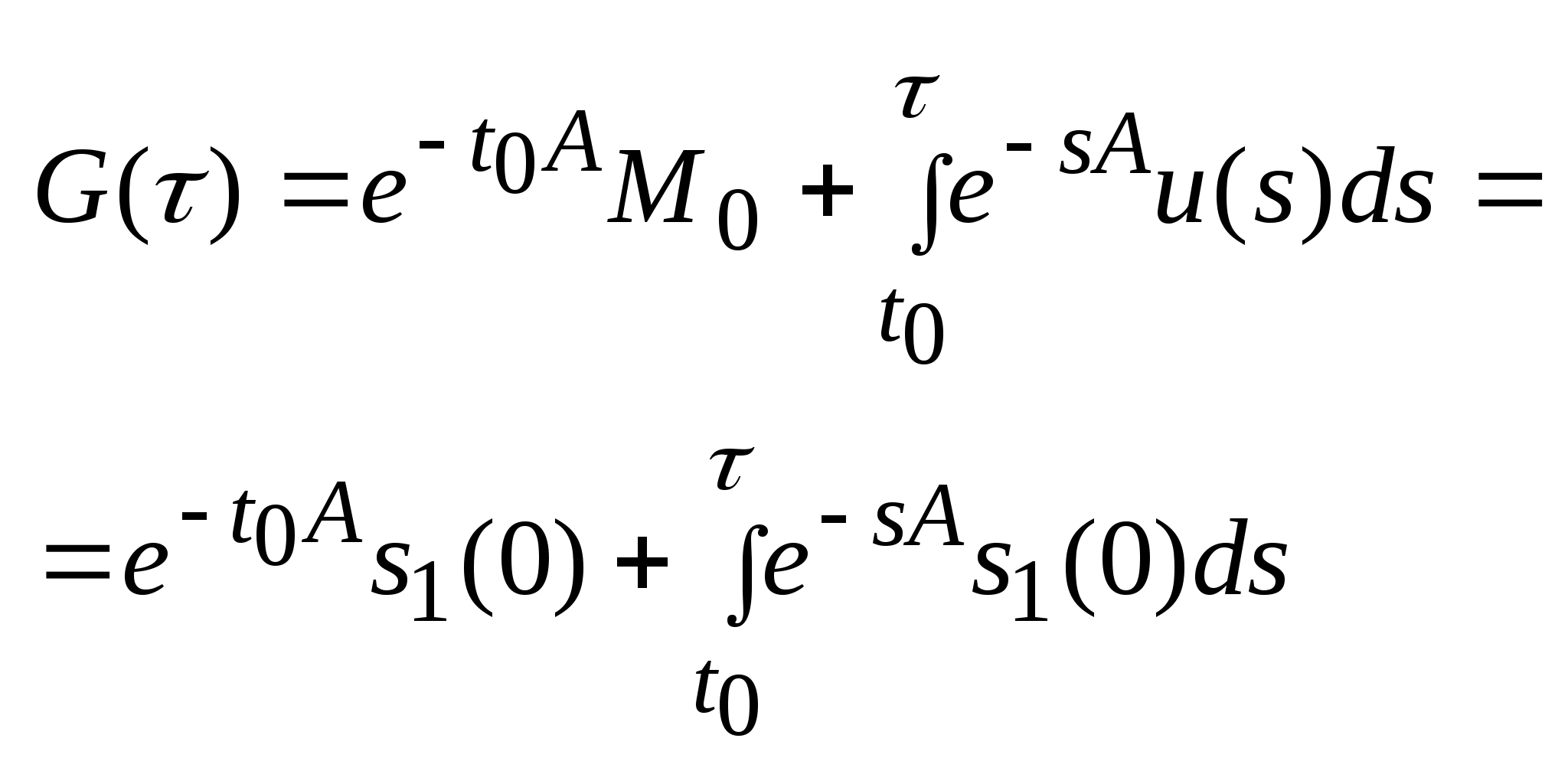 ,
,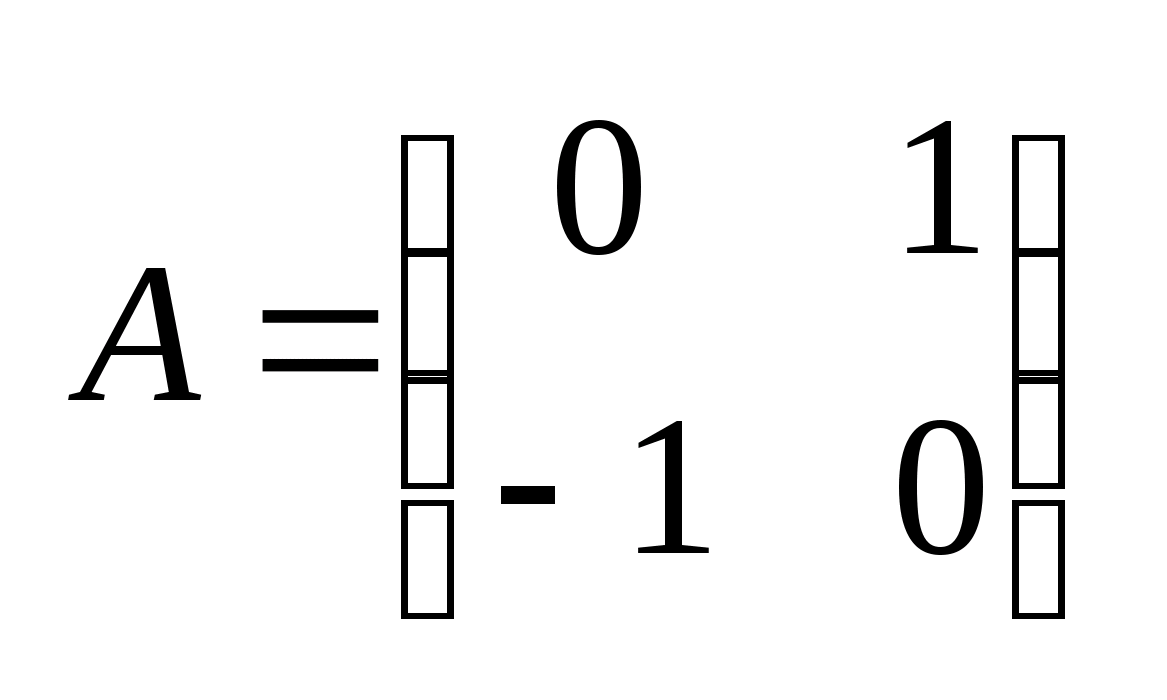 ,
,
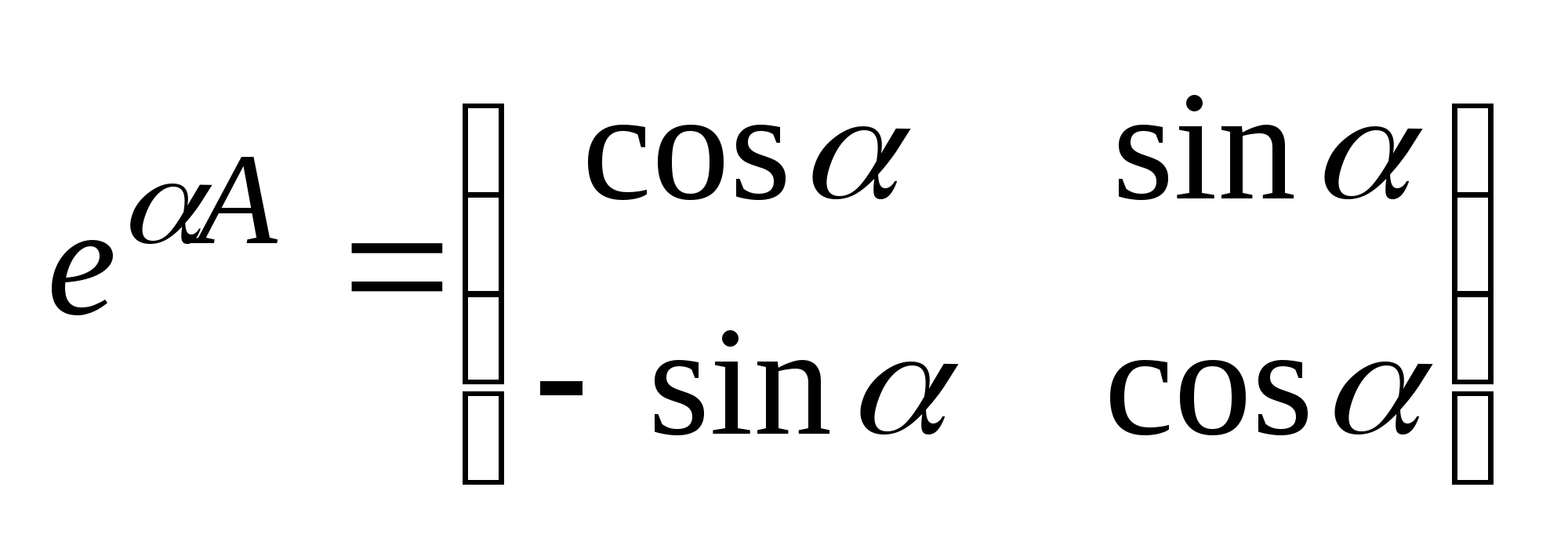 ,
,
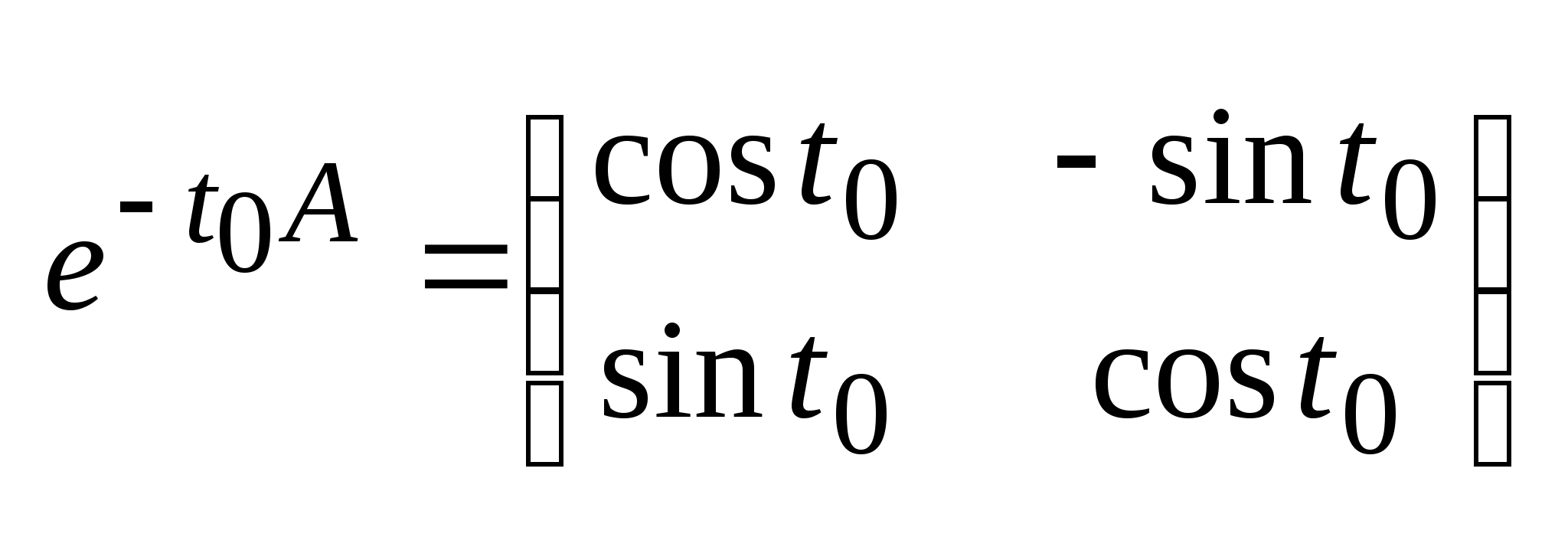 ,
,
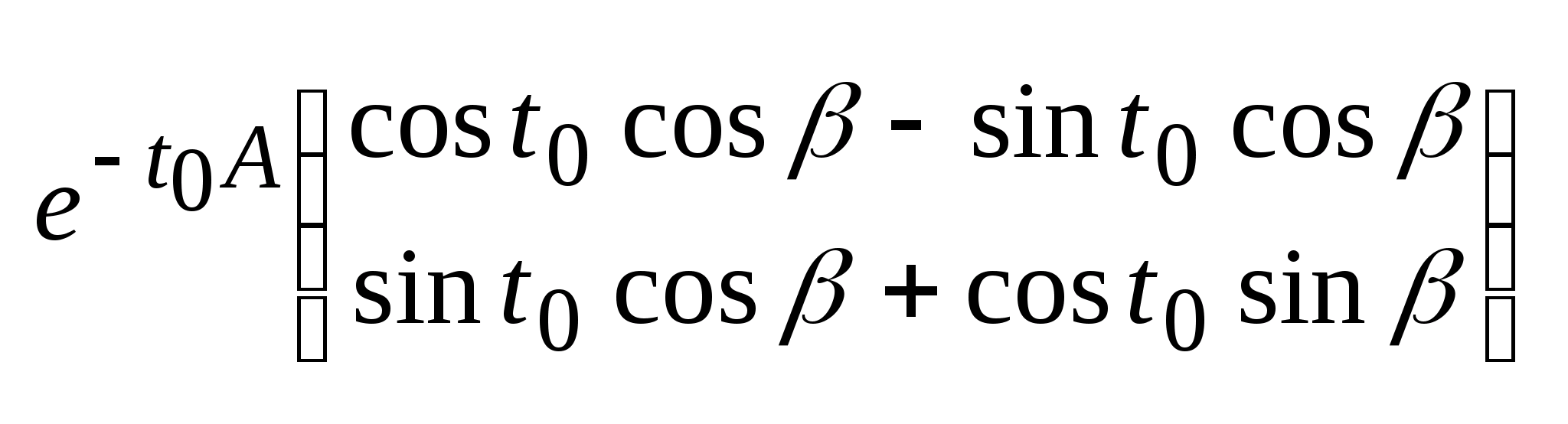 ,
,
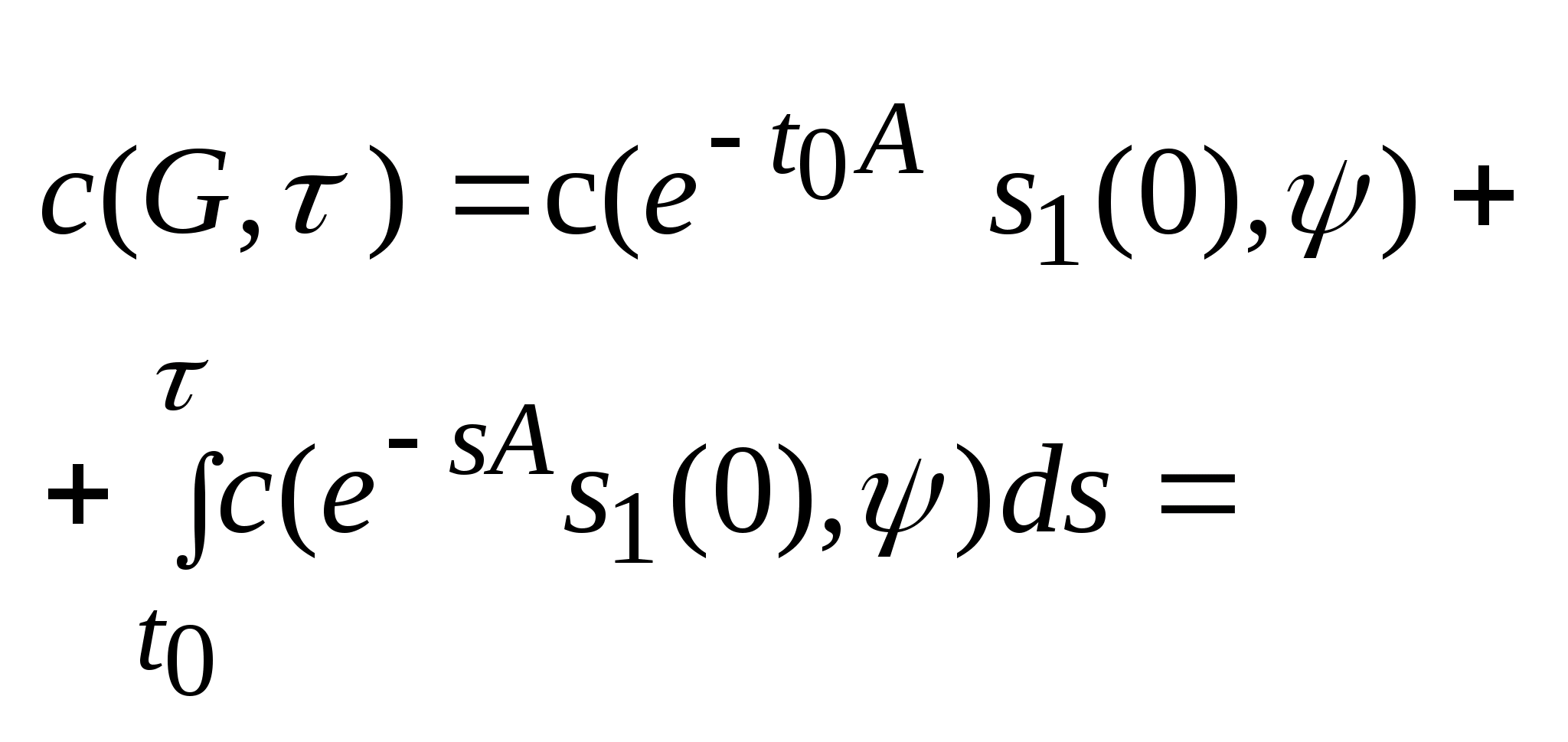
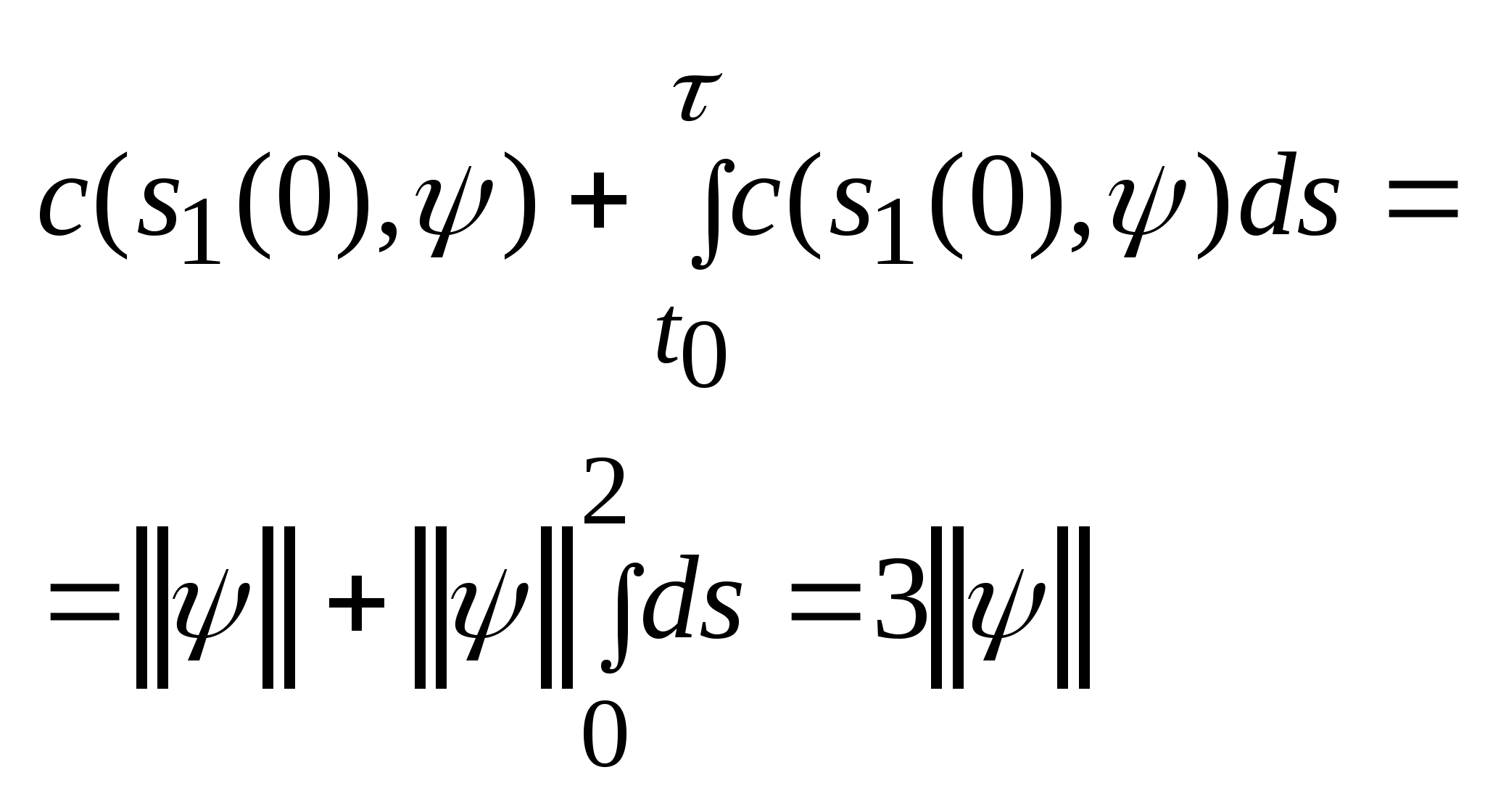 .
.
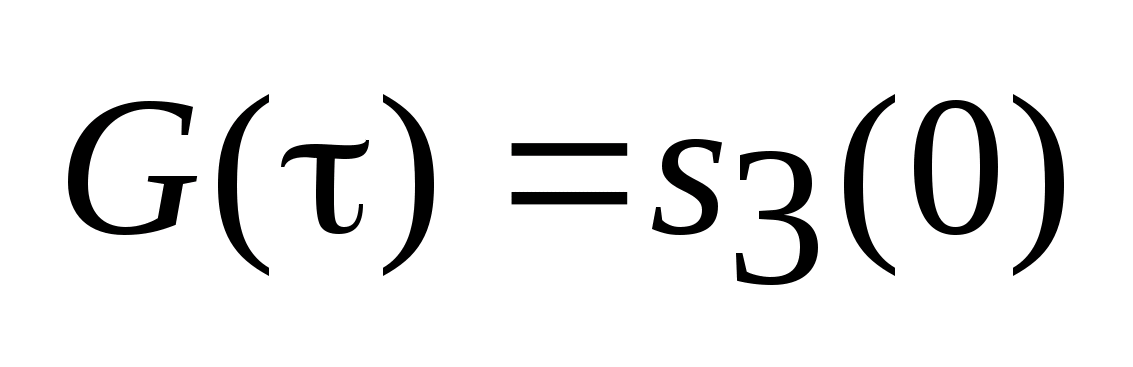 ,
,
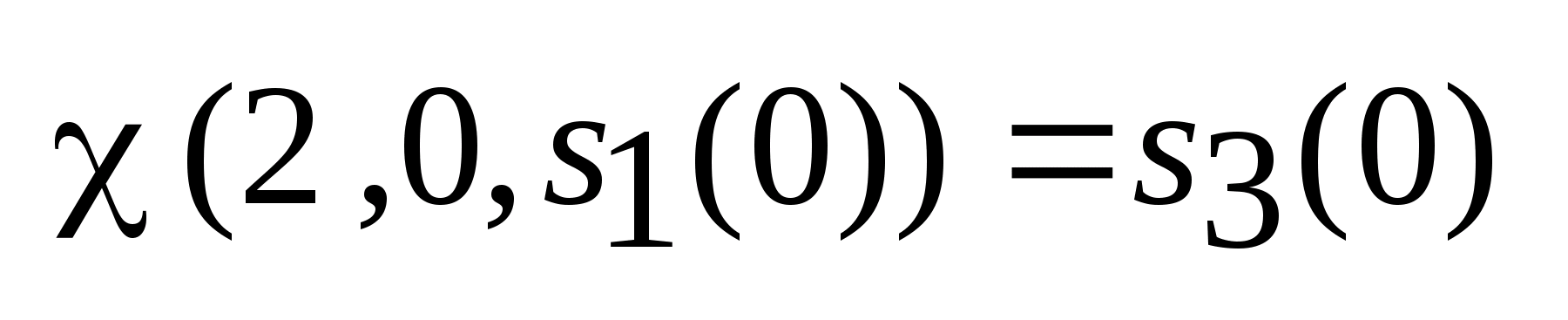 .
.
16. Общая задача управляемости. Теорема об управляемости.
Рассмотрим вопрос: «Оптимален ли объект?»
Рассматриваем
динамический объект, поведение которого
описывается системой (1)
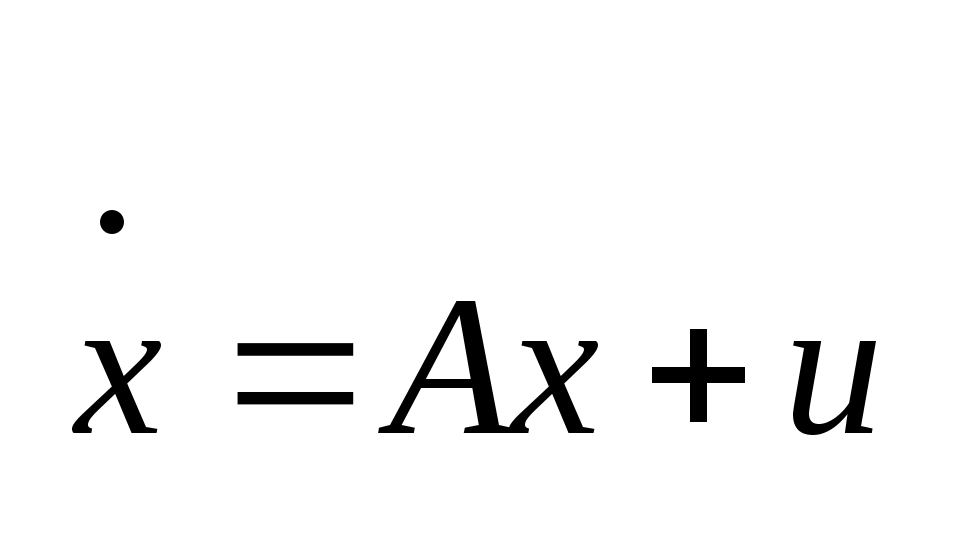 ,
x-
n-мерный
вектор,
,
x-
n-мерный
вектор,
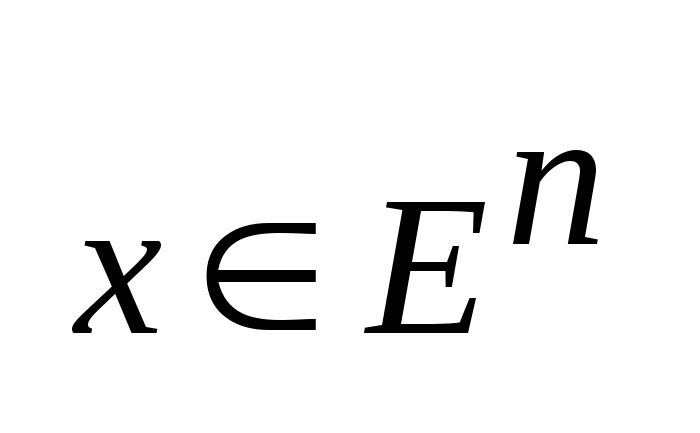 ,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
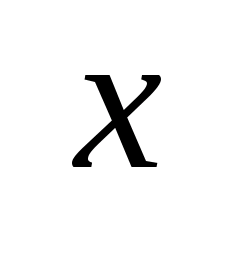 ,
,
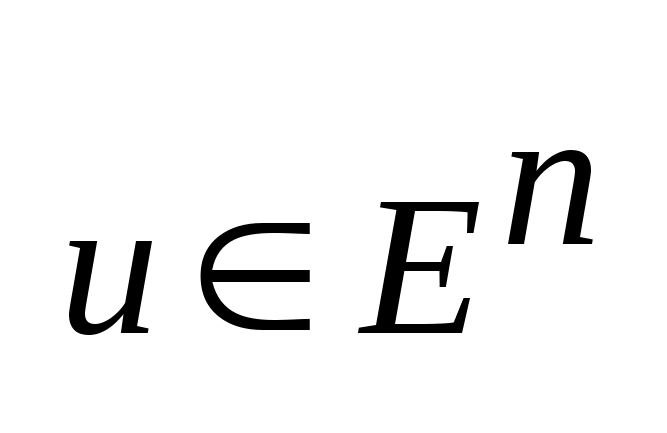 .Задано
.Задано
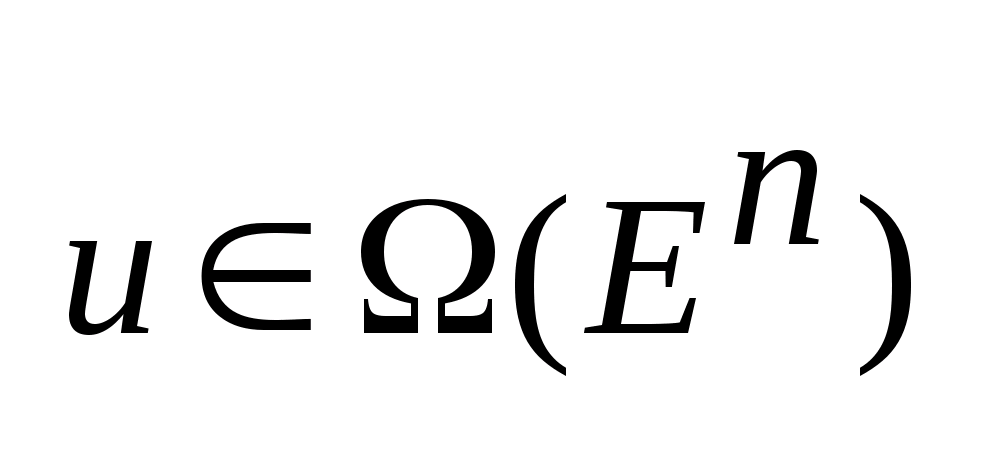 ,
u:
I
,
u:
I
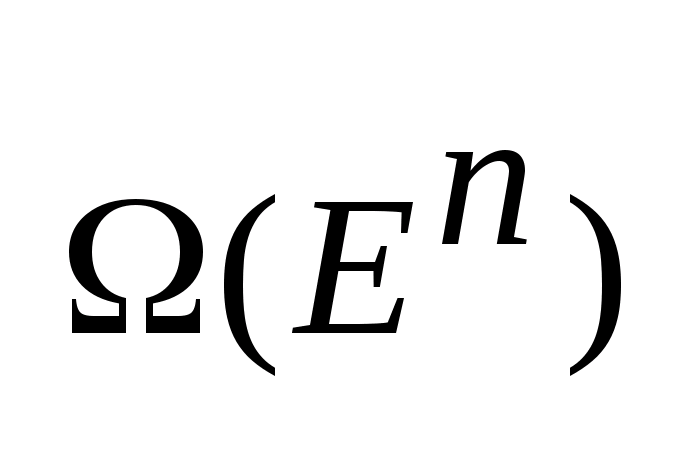 и полагается, что u(t)
измеримо
и
и полагается, что u(t)
измеримо
и
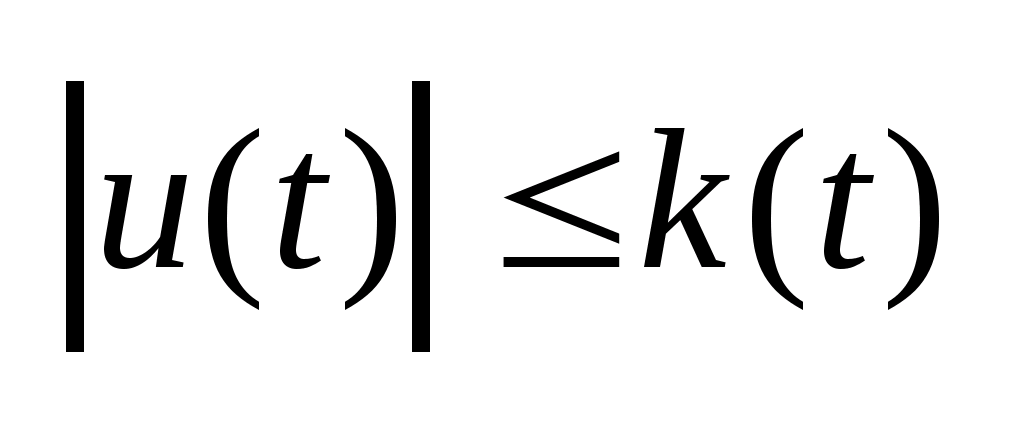 -
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью из многозначного отображения
U
(2) u(t)
-
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью из многозначного отображения
U
(2) u(t)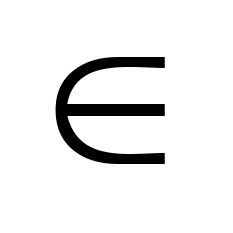 U(t)-
ограничения на управления . В фазовом
пространстве
U(t)-
ограничения на управления . В фазовом
пространстве
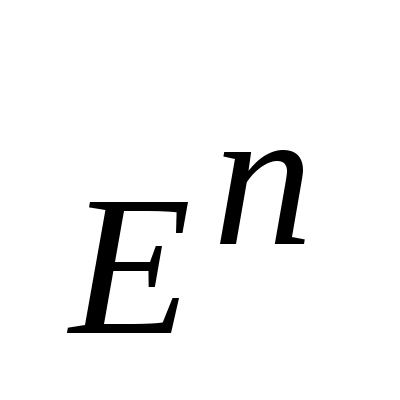 заданы
два не пустых множества
заданы
два не пустых множества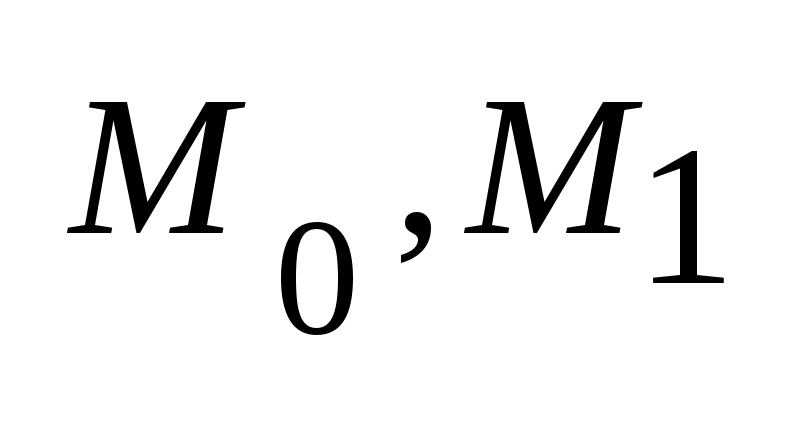
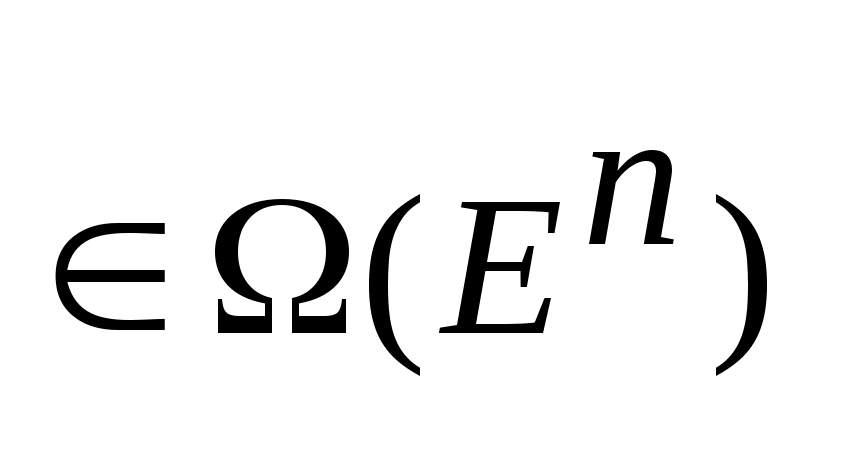 .
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
 в конечное множество
в конечное множество
 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
(4)
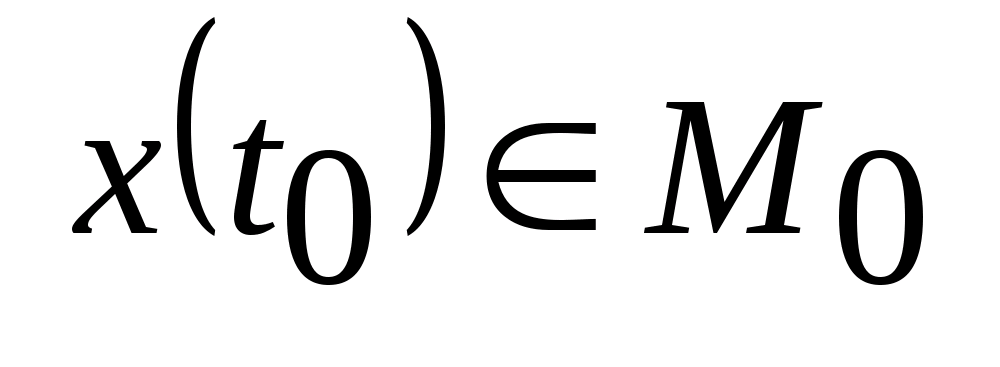 и
и
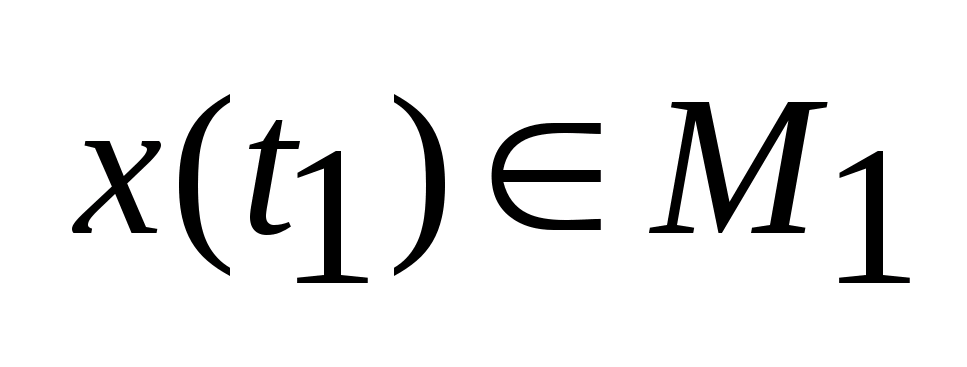 .
Цель управления- перевод динамический
объекта из
.
Цель управления- перевод динамический
объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача
быстродействия заключается в нахождении
такого допустимого управления, которое
осуществляет переход из множества
 в
в
 за
наименьшее время.
за
наименьшее время.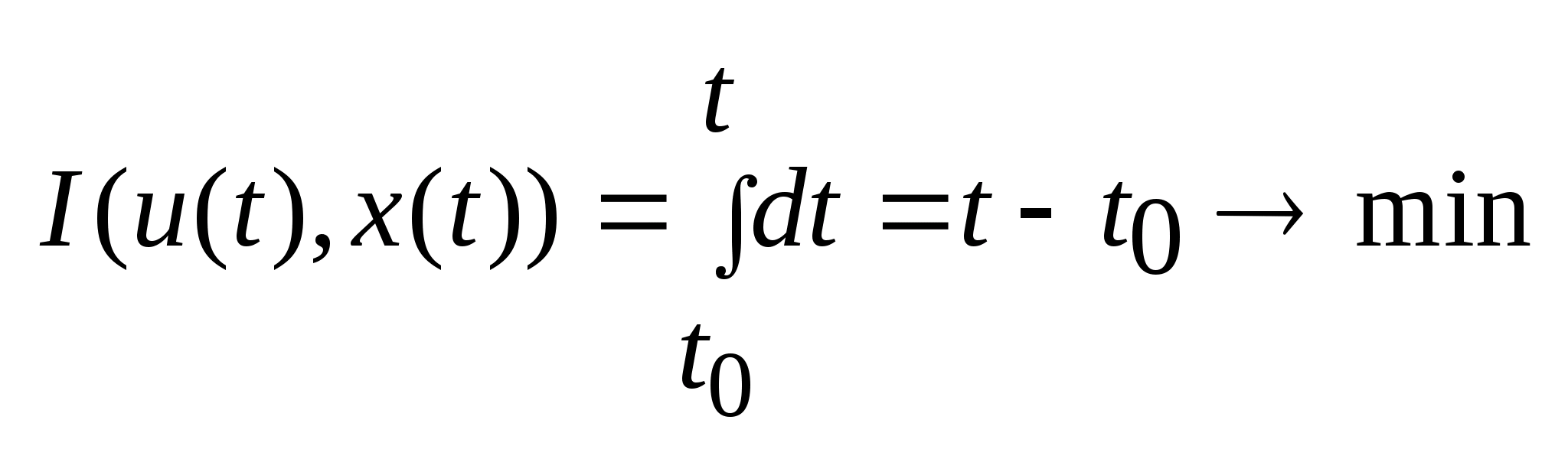 (4).
(4).
Задача
управления- решение вопроса :
существует хотя бы одно допустимое
управление u(t)
, переводящий
динамический объекта из
 в
в
 ,
на отр. времени I.
Это соответствует решению краевой
задачи:
,
на отр. времени I.
Это соответствует решению краевой
задачи:
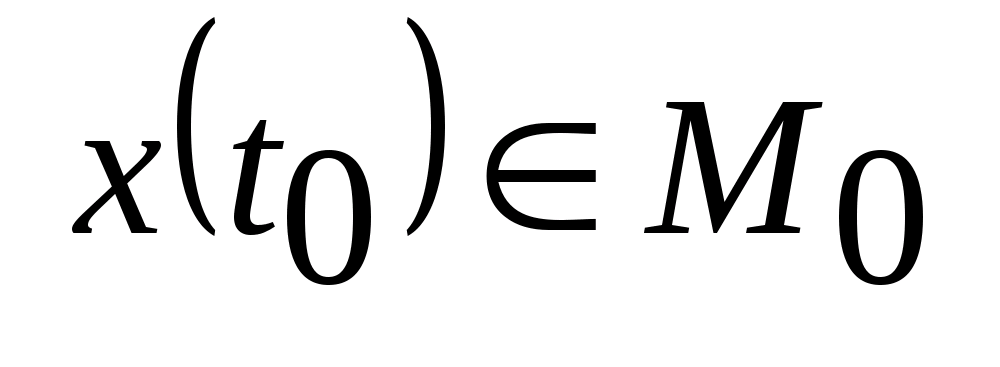 ,
,
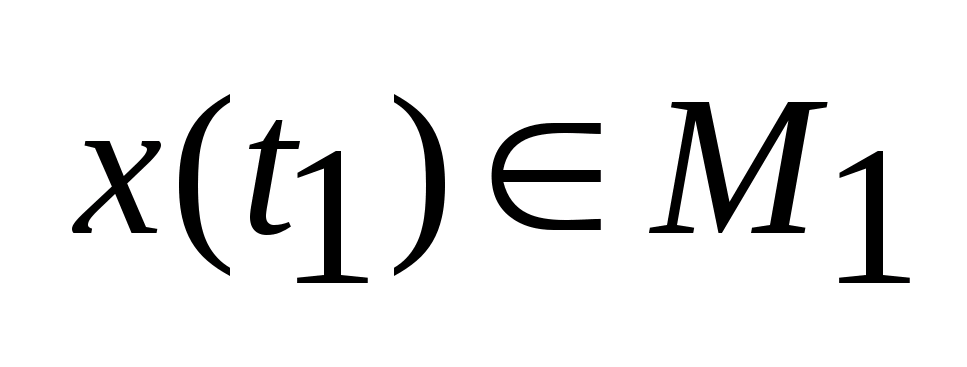 .
.
Определим
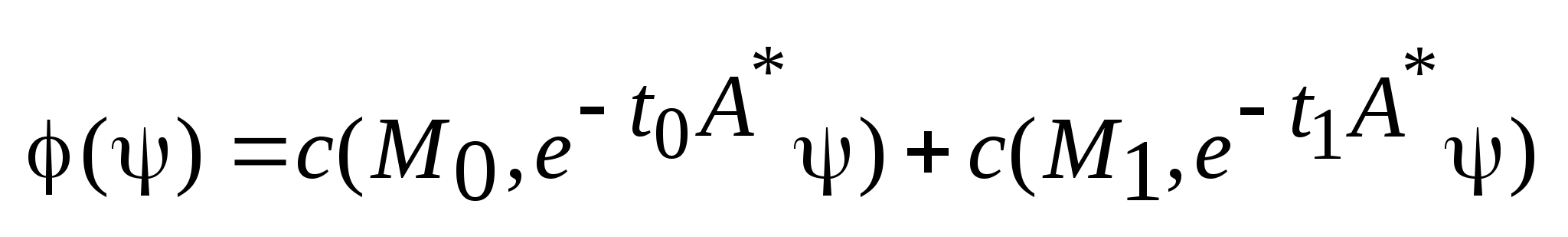
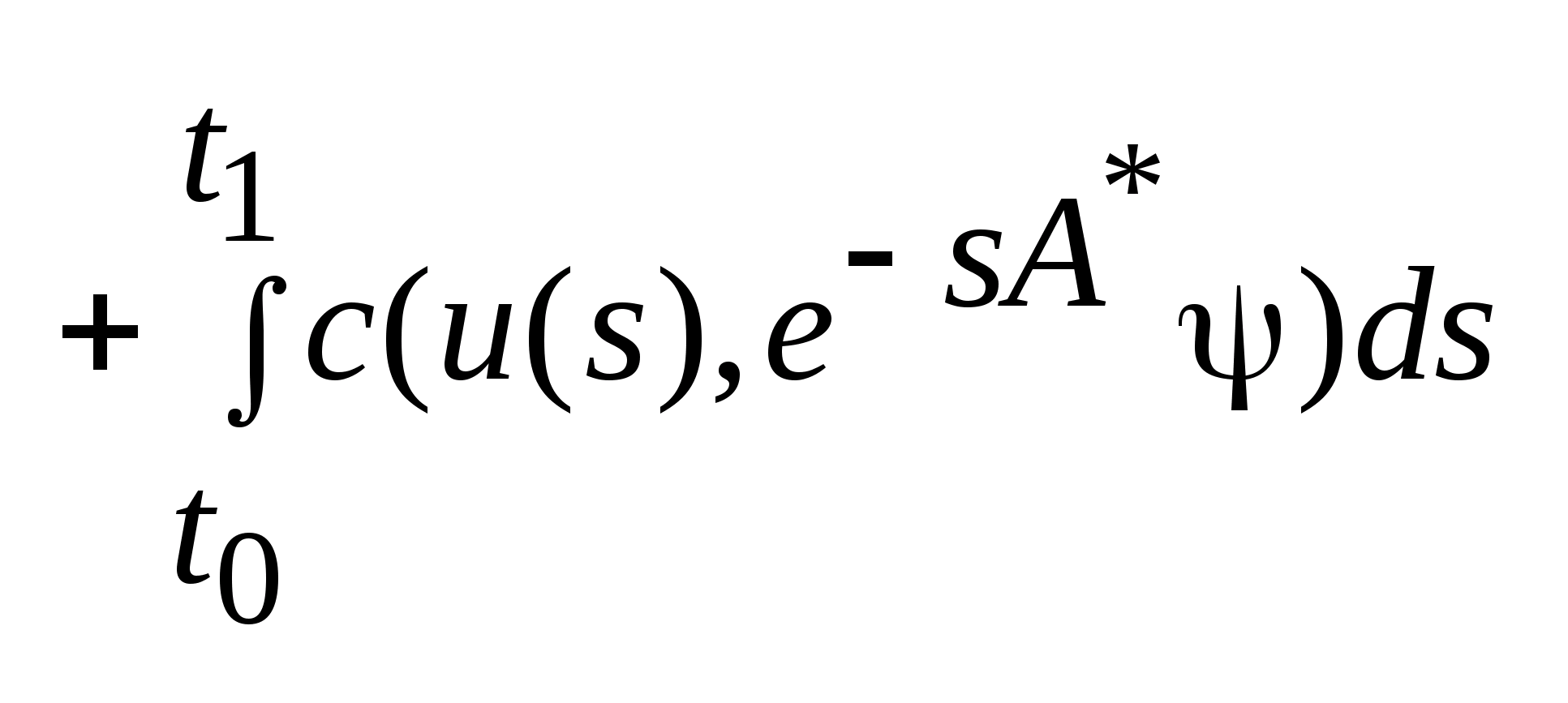 таким
образом.
таким
образом.
Теорема
об уравляемости.Если
 и
и
 выпуклы,
то объект явл. управляемым на отр. I
из мн-ва
выпуклы,
то объект явл. управляемым на отр. I
из мн-ва
 в
в
 ,
тогда и только тогда, когда для
,
тогда и только тогда, когда для
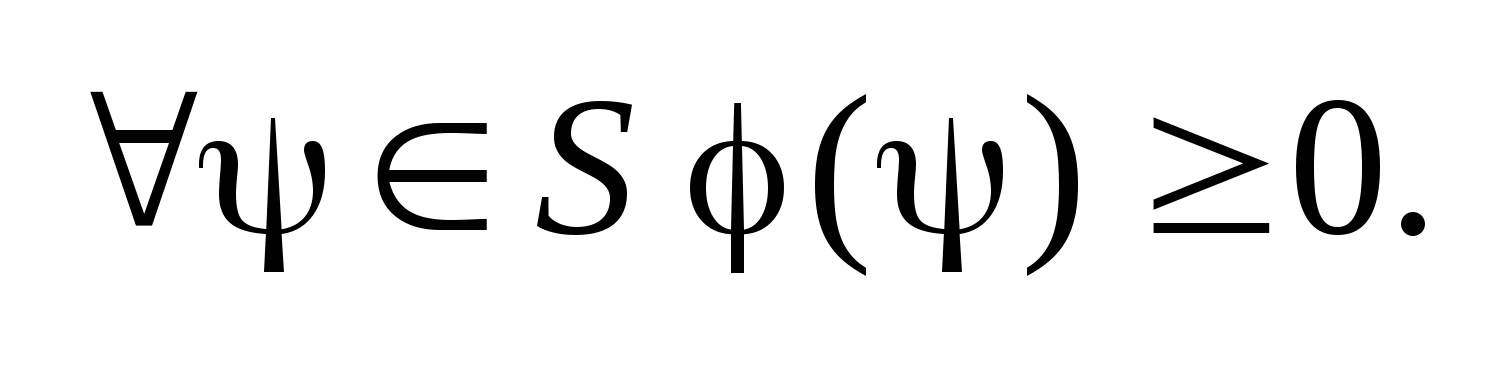
Док-во:
Очевидно, объект управляем тогда и
только тогда, когда множество достижимости
и
 пересекаются. Т.к.
пересекаются. Т.к.
 и
и
 выпуклы,
то для него применим следствие из 11
св-ва опорных фун-ий
(
выпуклы,
то для него применим следствие из 11
св-ва опорных фун-ий
(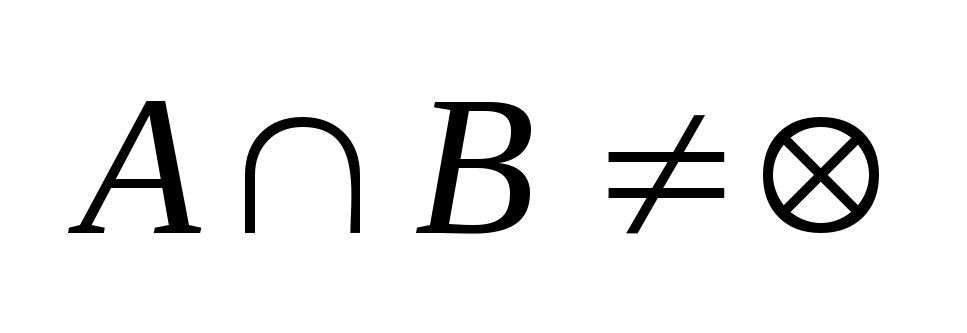
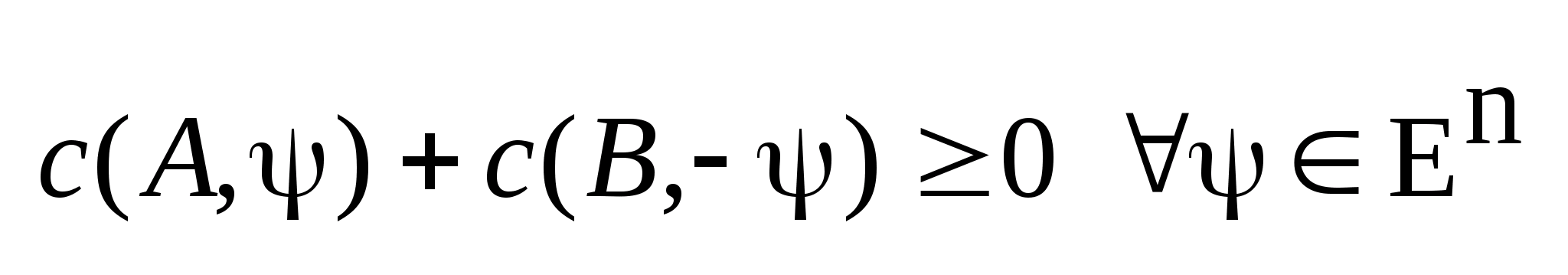 ).
).
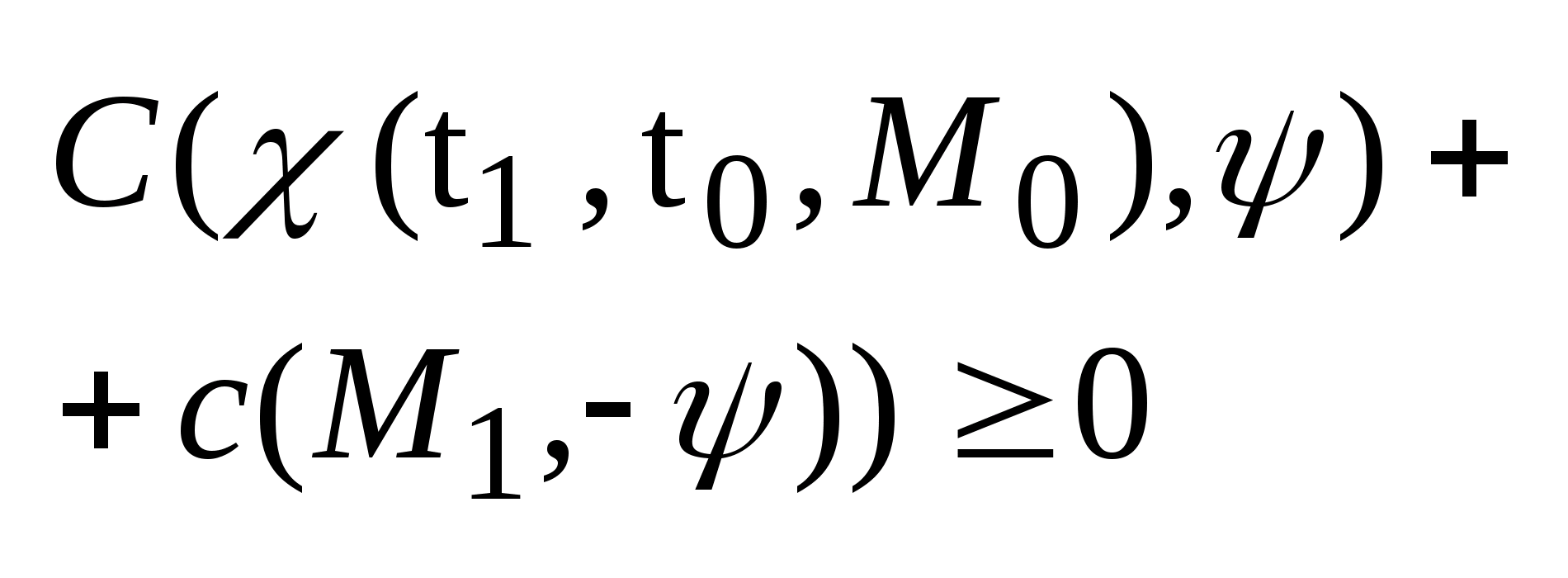 ,
,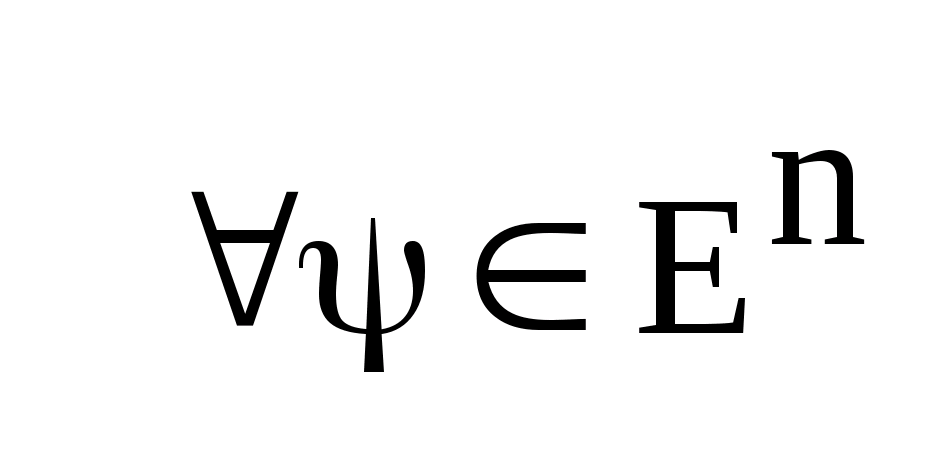 ;
;
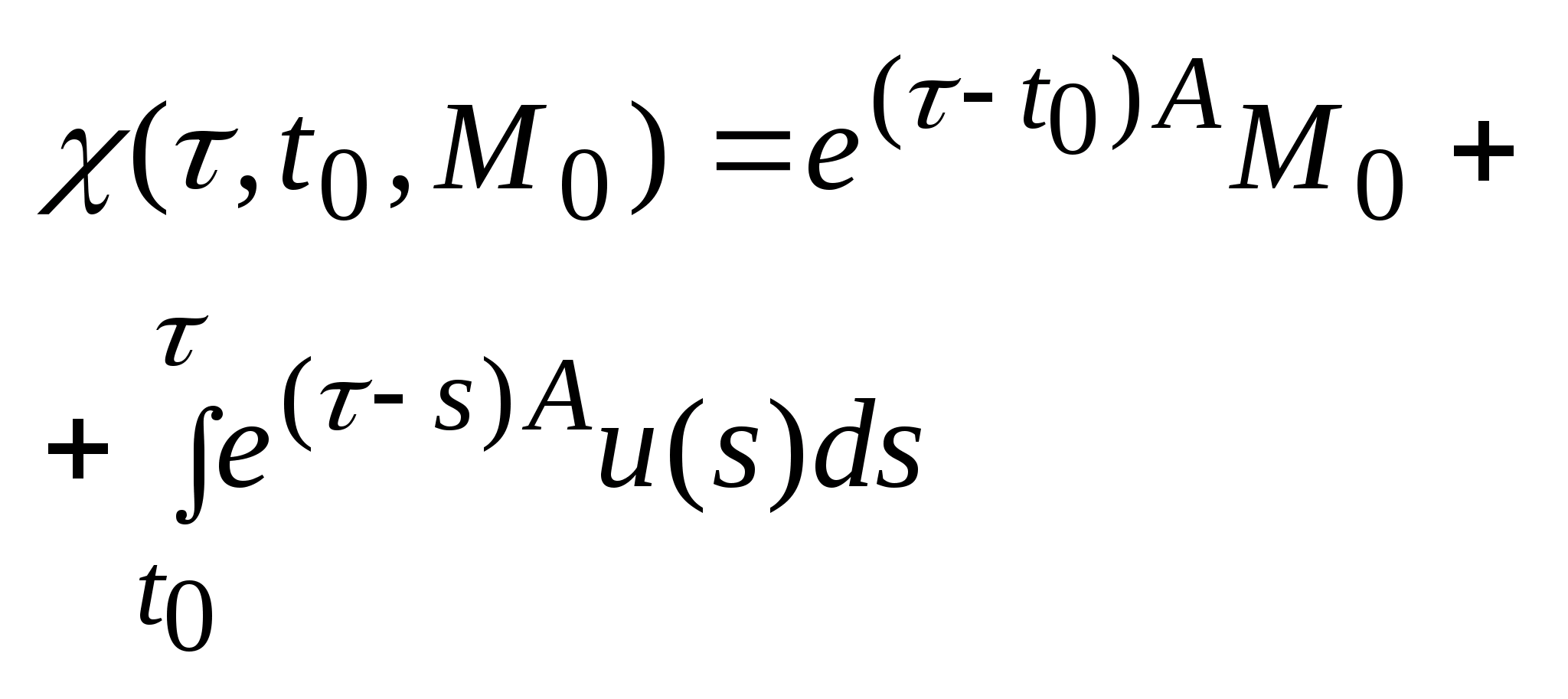
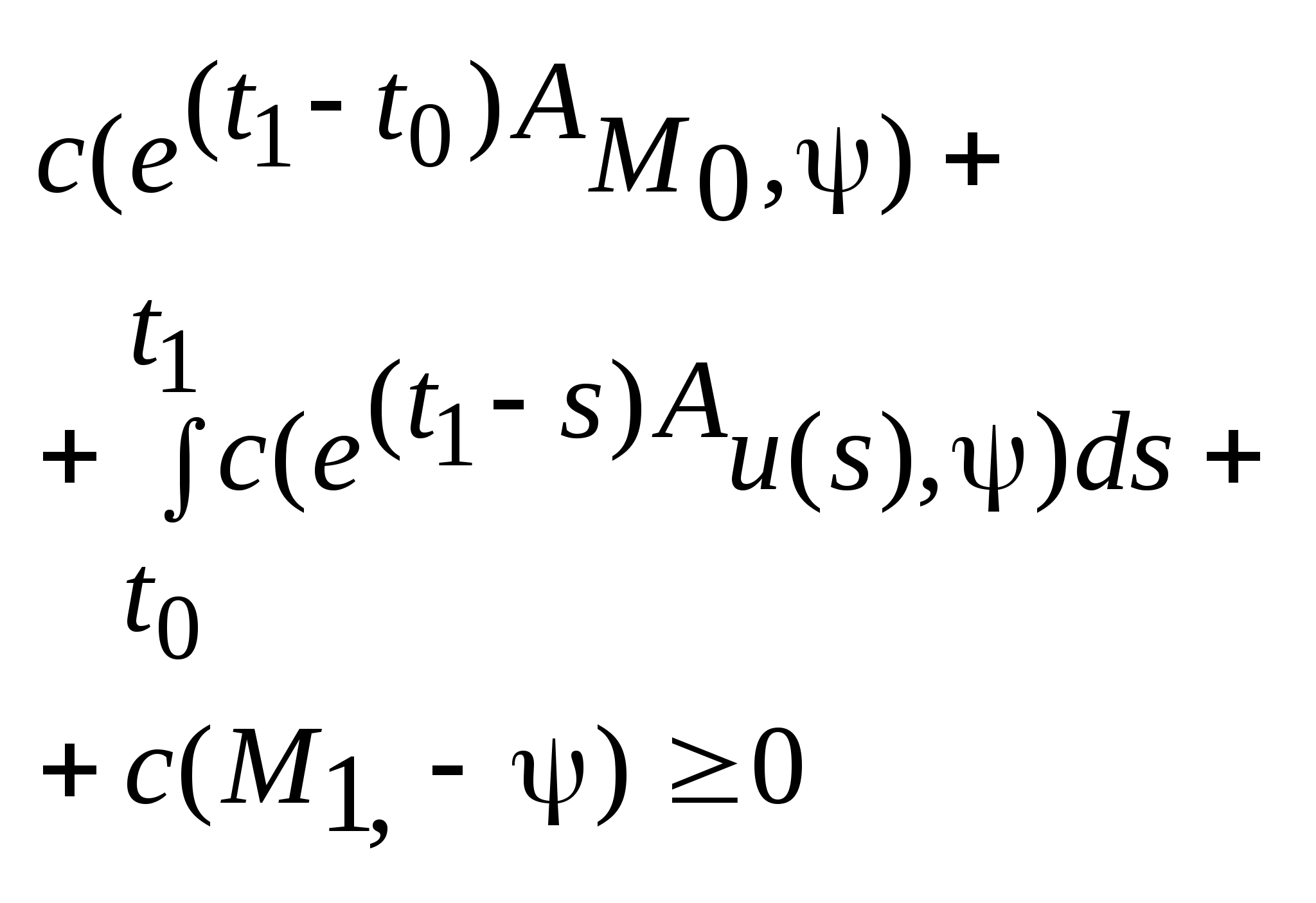 ;
;
Bocпользуемся
еще одним св-ом опрных функий: если
 -
невырожденная матрица, то можно
воспользоваться св-вом , что
-
невырожденная матрица, то можно
воспользоваться св-вом , что
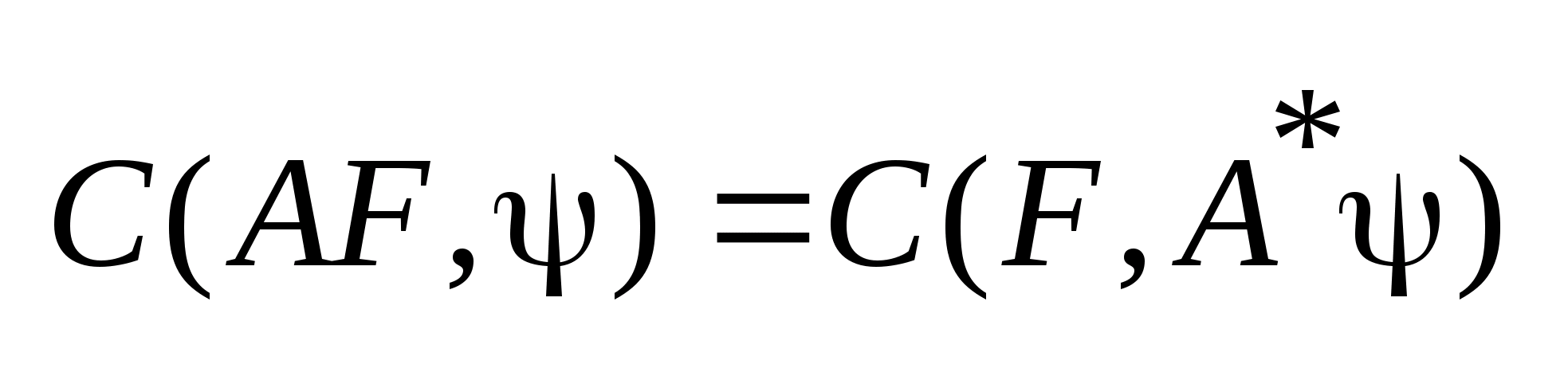 :
:
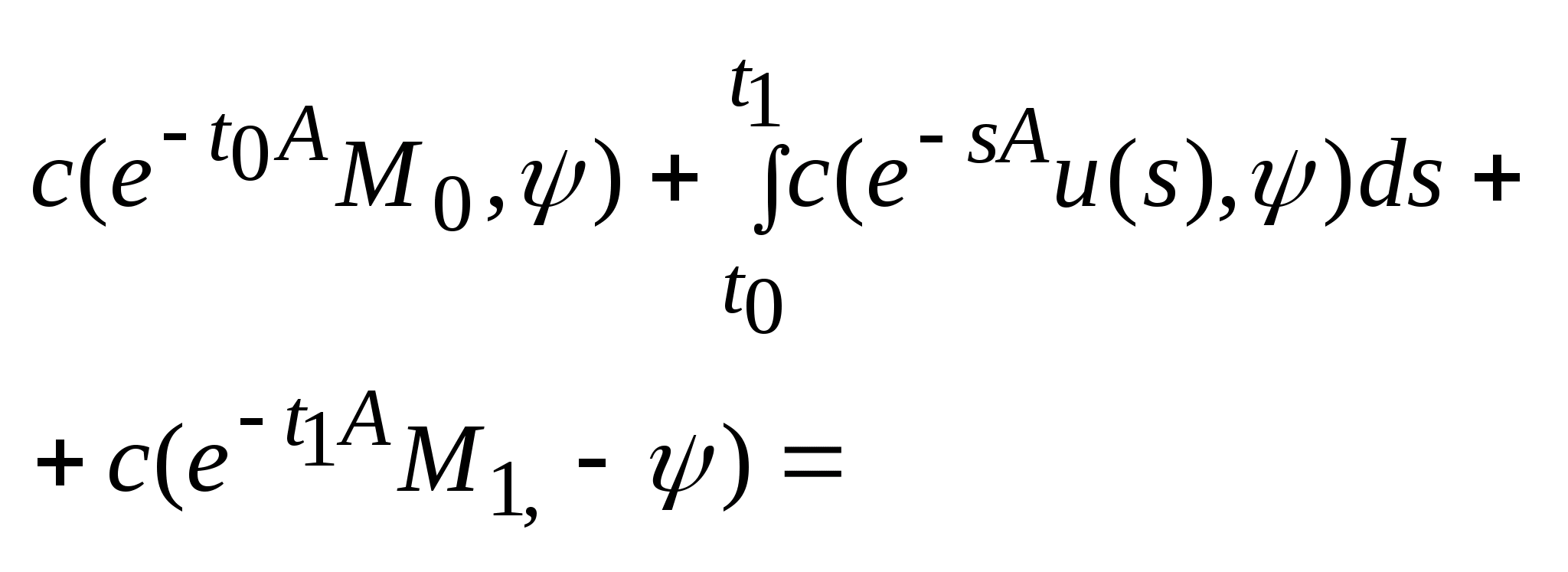
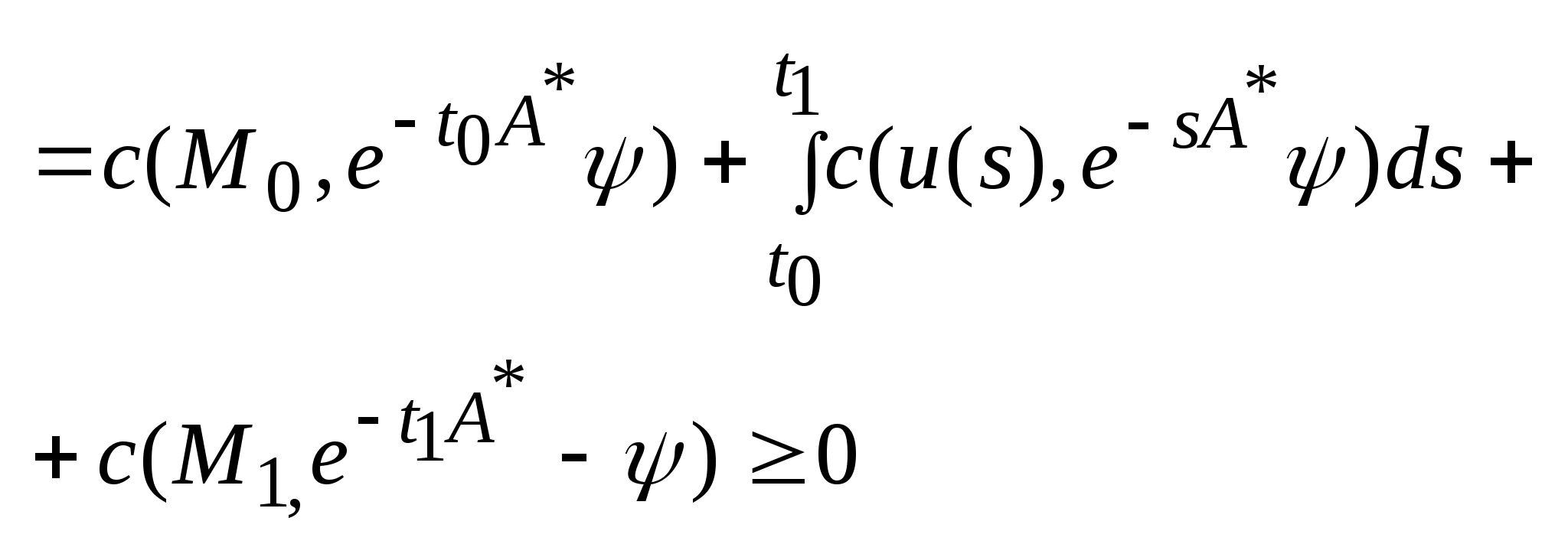
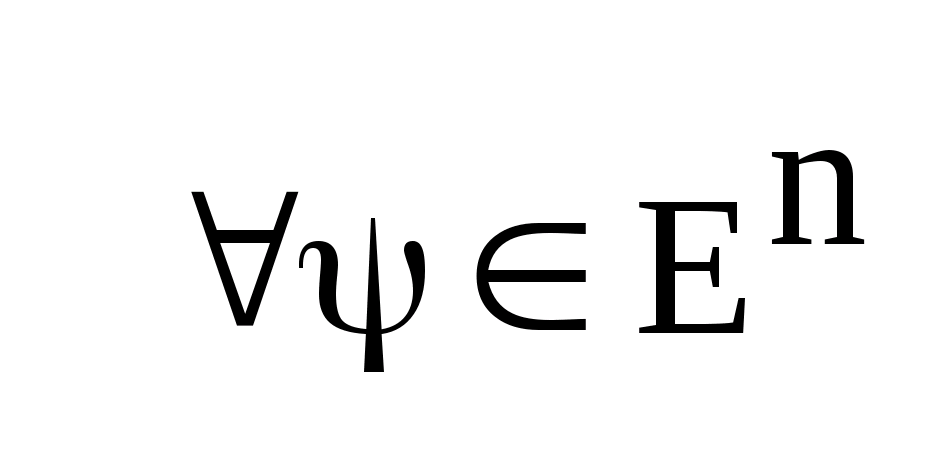 .
.
В
силу положительной опорной фун-ии
относительно аргумента
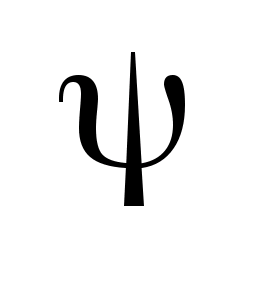 , получаем, что это верно
, получаем, что это верно
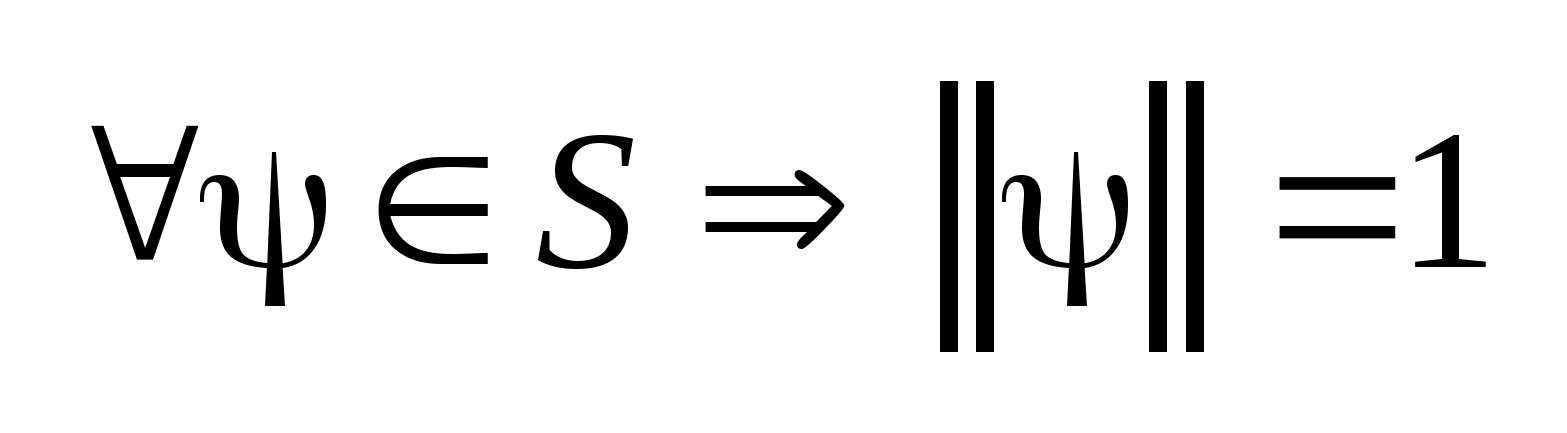 .
.
Теорема
док-на, т.к. левая часть неравенства и
есть
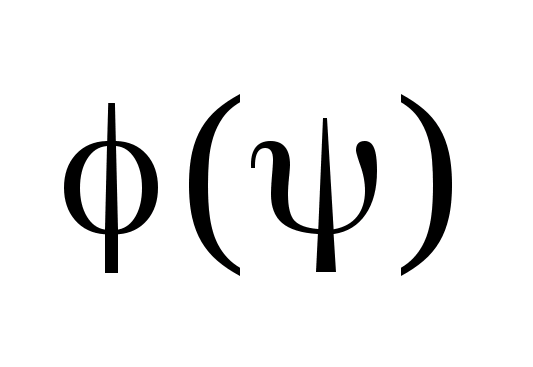 .
.
17.Численное решение задачи управляемости.
Объект
управляем на I=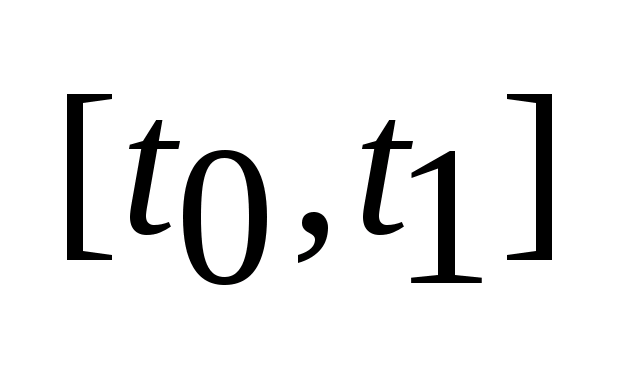 ,
если выполняется
,
если выполняется
 >
>
> >.
Если множнство >
>,>
>,
> >
таковы
что аналитически невозможно получить
значение опорной функции u
>
>
> >.
Если множнство >
>,>
>,
> >
таковы
что аналитически невозможно получить
значение опорной функции u
Вычисление матрицы > > и интеграл, тогда задача решается с применением ЭВМ. На ЭВМ решается для конечного числа > >. Для этого сфера покрывается > >-сетью. В двумерном пространстве > >-сеть определяется углом > >. В трехмерном пространстве > >-сеть определяется двумя углами. Пусть > >некоторая > >-сеть некоторой единичной сферы S, где > >-конечное множество. Какой бы вектор > >, найдется > >, такой что > >. Пусть > >вычислимое приближенное значение > > в точках > >-сети. > >, > >. Необходимо, чтобы > >- в этом случае говорим, что объект > >-управляем и при этом > >. Отсюда имеем следующее > >. Если > >, то > >-объект E-управляем. Если > ><0, то > ><> >-объект не управляем. Если > >, то в этом случае неопределенность. Выясним вопрос о погрешности.> >и > >-погрешность для вычисления опорной функций > >и > >.> >- погрешность для вычисления > >. По условию Липшица > >,
> >. Используем эти формулы , получим следующие погрешности: > > - погрешность для вычисления > >-предполагается, что она интегрируема по Лебегу. > >-это вычисление интеграла > >. > >- погрешность для вычисления > >. > >-погрешность вычисления минимума функций. > >, > >. > >+> >+> >+> >+> >+> >+> >+> >
18. Лемма о внутренней точке.
Пусть А- квадратичная матрица размера nxn , V-произвольный вектор пр-ва> >, отрезок I=> >. Тогда > >, тогда и только тогда , когда векторы > >линейно независимы.
Под интегралом- многозначное отображения, интеграл от многозначного отображения – тоже многозначное отображения.
Доказательство : Обозначим F=> >. По свойствам опорной функции для того чтобы > >нужно, чтобы выполнялось условие > >, > >. > >> >> >=> >
=> >=
=> >=> >.Т.к. подынтегральная функция непрерывна и неотрицательна, то условие > >, > > выполняется тогда и только тогда, когда > > на интервале I . Покажем, что для этого необходимо и достаточно, чтобы векторы > >были лин. независимы.
Необходимость: (доказательство от противного)
> > эквивалентно > >, > >-лин.независимы .Предположим, что векторы > > лин. зависимы. Для 3-х векторов : > >; > >- лежат в одной плоскости, > >> >; > >. Тоже самое для n- векторов: > >, > >> >> >Пришли к противоречию, необходимость доказана.
Достаточность: (от противного)
Если векторы линейно независимы, то > > такой, что > >, > >. Продифференцируем > >n-1 раз:0= > >.Отсюда следует: > >, где > >- невырожденная матрица, > > -не нулевой вектор и > >, а это означает, что векторы > > лин.зависимы .Получили противоречие. > >перпендикуярен > >.
19. Локальная управляемость. Теорема о локальной управляемости..
Рассматриваем динамический объект, поведение которого описывается системой (1) > >, x- n-мерный вектор, > >, A-матрица nxn, u имеет ту же размерность, что и > >, > >.Задано > >, u: I> >> > и полагается, что u(t) измеримо и > >- где k(t) скалярная функция интегрируемая по Лебегу на отрезке I .Функция u(t)- называется допустимым управлением, если измерима и является однозначной ветвью из многозначного отображения U (2) u(t)> >U(t)- ограничения на управления . В фазовом пространстве > >заданы два не пустых множества> >> >. Допустимое управление u(t) на отр.I осуществляете переход из начального мн-ва > > в конечное множество > >, если существует решение уравнения (1), удовлетворяющее граничным условиям (4) > >и > >. Цель управления- перевод динамический объекта из > >в > >, а качество определяет функционал. Таким функционалом явл. время, следовательно
задача быстродействия заключается в нахождении такого допустимого управления, которое осуществляет переход из
множества > >в > >за наименьшее время.> > (4).
Предположим, что > >, а мн-во > >-произвольные точки > >из окрестности > >> >.
Сделаем линейную замену:> >,где > >-функции, получим > >, > >, где > >,> >, поэтому вместо точки > >можно рассматривать т.0 и будем говорить о локальной управляемости в т.0. Т.е. если объект локально управляем в т.0, то он локально управляем в любой точки > >.
Определение: Объект наз. локально управляем в т. > >=0 на отр.I , если > > объект явл. Управляемым на отр.I из т.> >.
Для решения задачи применим теорему об управляемости, но для конкретной местности. Исходя из теоремы об управляемости, объект явл. управляемым из > >в > > на I , если > >>=0.
20. Теорема о локальной управляемости. (дает достаточное условие локальной управляемости)
Если > >вектор > > и выполняются два условия:
1)> >, > >;
2) > >-лин. независимы, тогда объект явл. локально управляем в точке x=0 на отр. I.
Доказательство: В силу определения локальной управляемости выполняется условие > >> >.
> >, получим (1) > >> >. Покажем, что > >, такое , что выполняется (1) > >и > >. По предположению теоремы 1) выполняется > >, получим > >. Сделаем оценку для левой части неравенства. Оценим интеграл: > >,
т.к. > > и выполняется 2) , то 0 явл. внутренней точкой интеграла:> >, а это означает, что опорная функция >0, > >. Из свойств опорной функции следует, что опорная функция непрерывна по > >. Если опорная функция непрерывна, >0, и S –компактное, это означает, что > >, такое что , > >, > >. Т.о. оценили левую часть неравенства (1), покажем , что для правой части , которая зависит от > >, по этому > >можно найти > >.
Покажем , что > >. Оценим
> >
, отсюда имеем > >> >.
> >,> >, а это значит , > >объект локально управляем в точке x=0.
21. Теорема о существовании оптимального управления.
Если объект является управляемым из множества > > на отр. > >, то существует > > переводящее объект из > > за время > >- оптимально управляем.
Рассмотрим > > -множество всех допустимых управлений, переводящих объект из > >. Т.к. объект является управляемым , то > >. Обозначим через > >попадания фазового вектора > >на множестве > >, т.е. > >. Следовательно за меньшее > >невозможно перейти.
Докажем, что > >, переводящее объект из > >за > >, при этом > >считается фиксированым. Т.к. > >, то > >последовательность > >перехода, сходящаяся к > >. > > удовлетворяет мн-во достижимости > >(пустое мн-во). Пусть для > >> >. Т.к. множество > >замкнуто и ограничено, то из > >можно выбрать подпоследовательность > >.
Пусть дано > >. Т.к. > >сходящаяся к> >.
Т.о. > >. Множество > >непрерывно по аргументу > >, т.е. начиная с какого-то номера > > > >. > >. Т.к. > > произвольная, а мн-во > >компактно, то > >. Т.к. > >и > >, то это обозначает, что > > (пустое мн-во) и это означает, что > >, переводящее объект из > >за > >. И т.к. > >, то > >- оптимальное управление. Теорема док-на.
22. Принцип максимума Понтрягина на языке опорных функций.
Рассматриваем
динамический
объект, поведение которого описывается
системой (1)
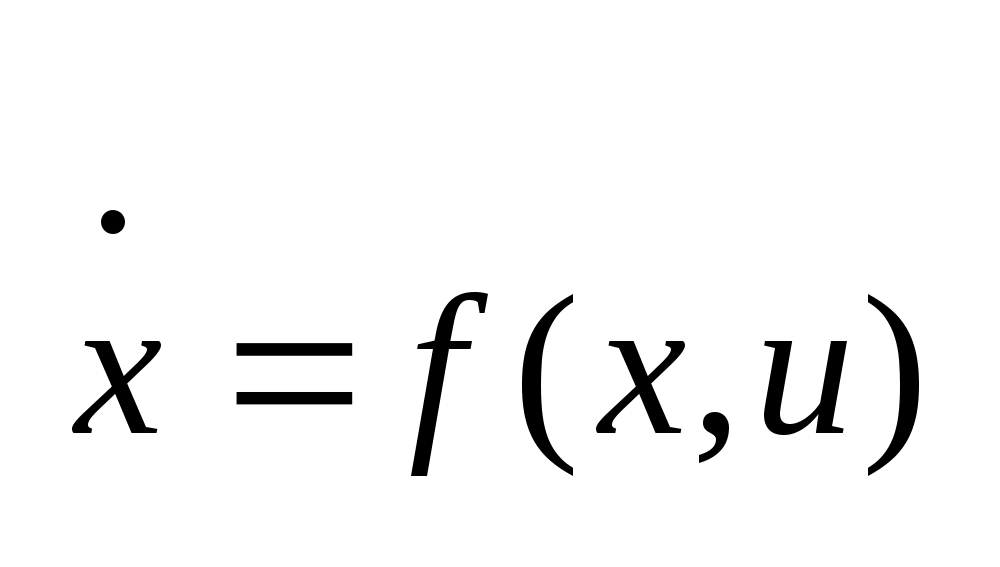 ,
x-
n-мерный
вектор,
,
x-
n-мерный
вектор,
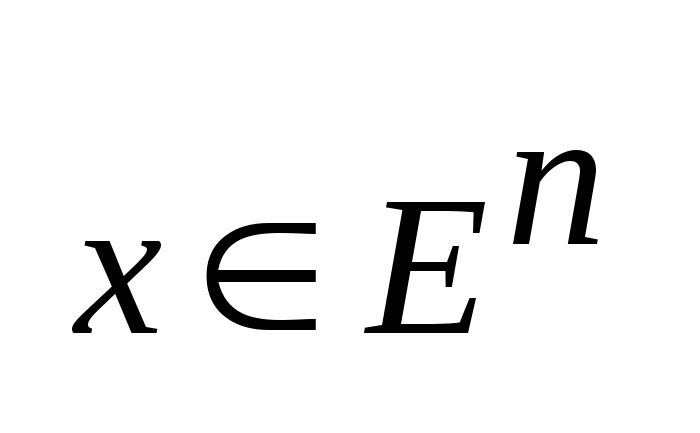 ,
,
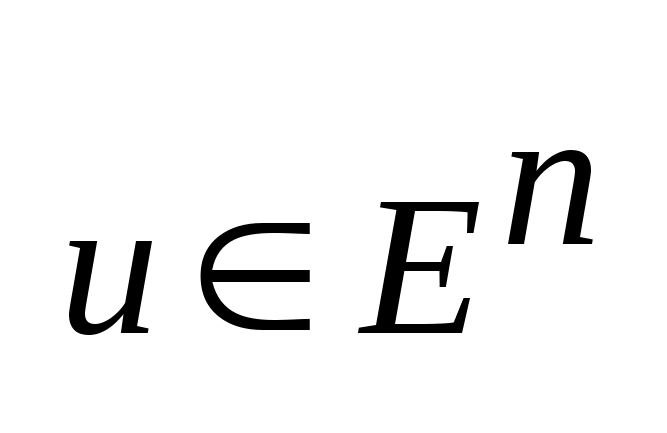 .Задано
.Задано
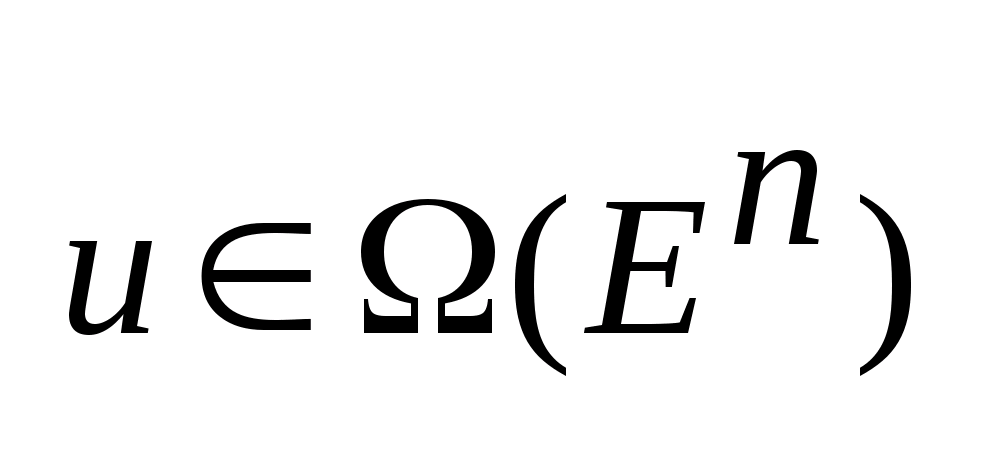 ,
u:
I
,
u:
I
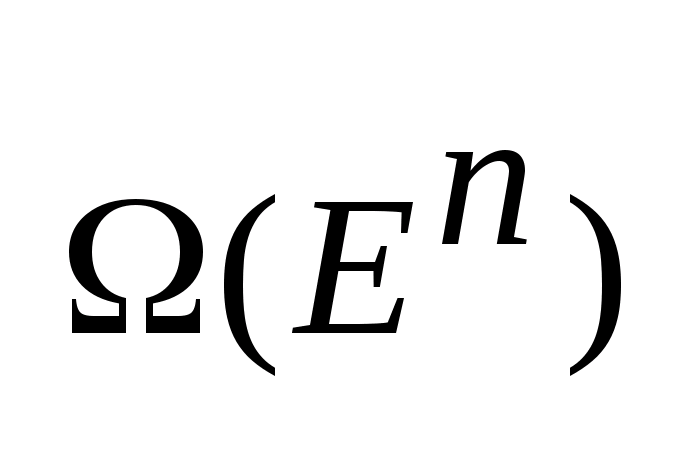 и полагается, что u(t)
измеримо
и
и полагается, что u(t)
измеримо
и
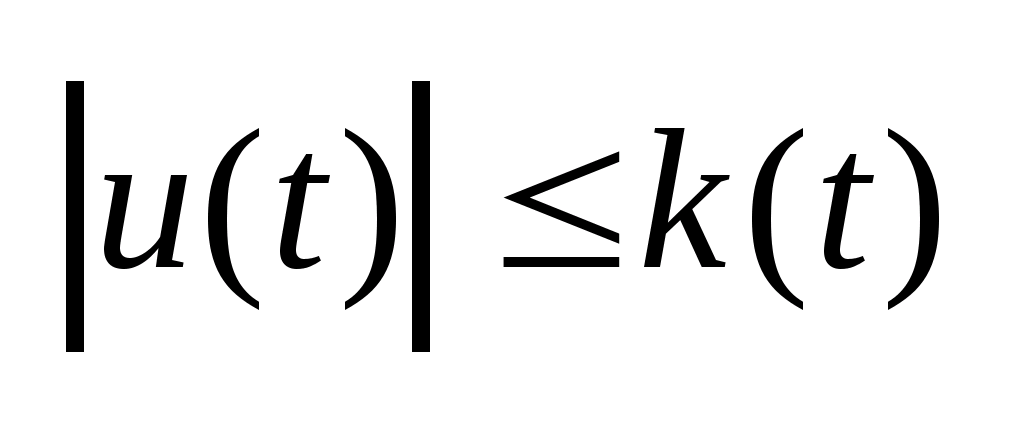 -
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .
В фазовом пространстве
-
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .
В фазовом пространстве
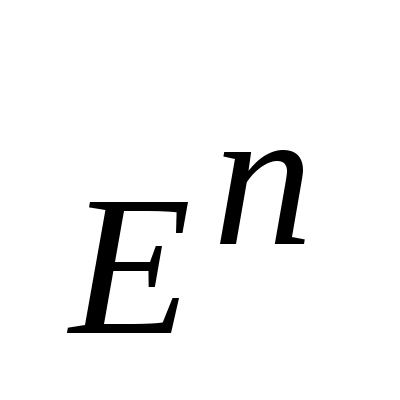 заданы
два не пустых множества
заданы
два не пустых множества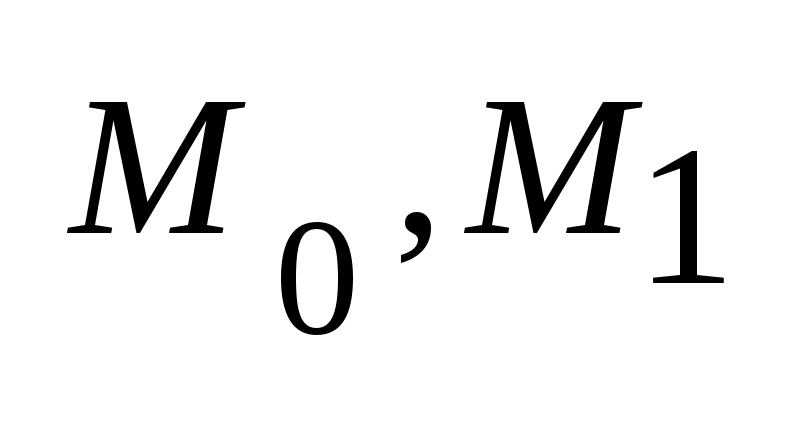
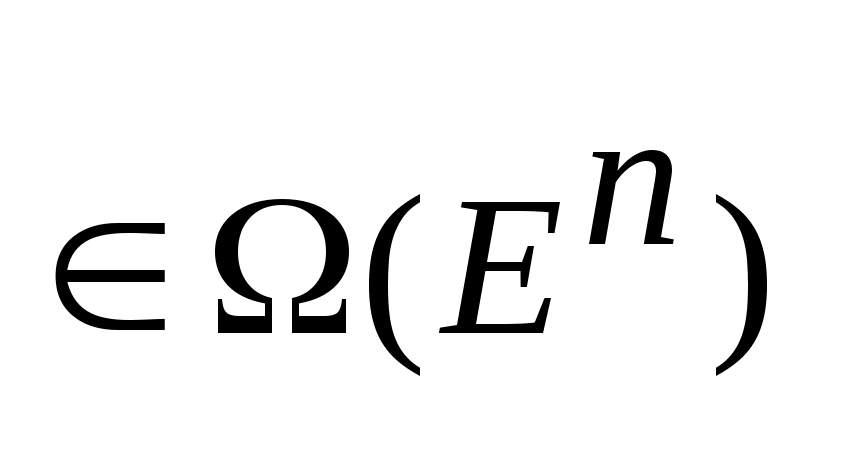 .
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
 в конечное множество
в конечное множество
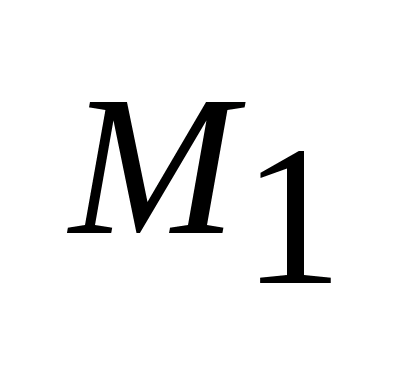 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
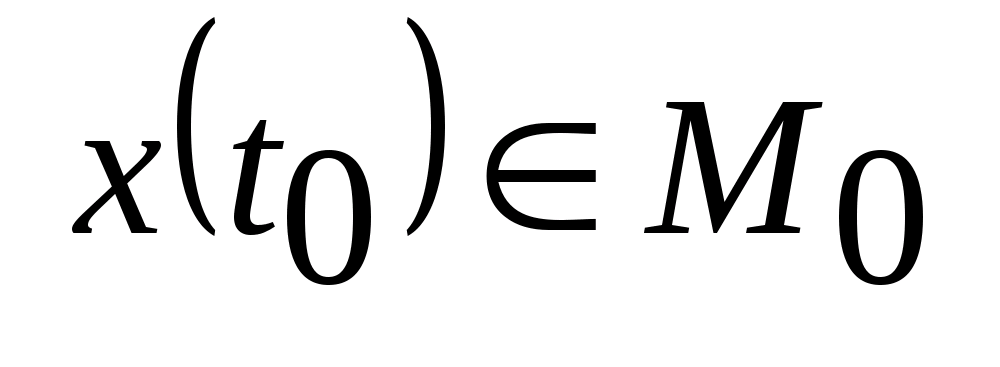 и
и
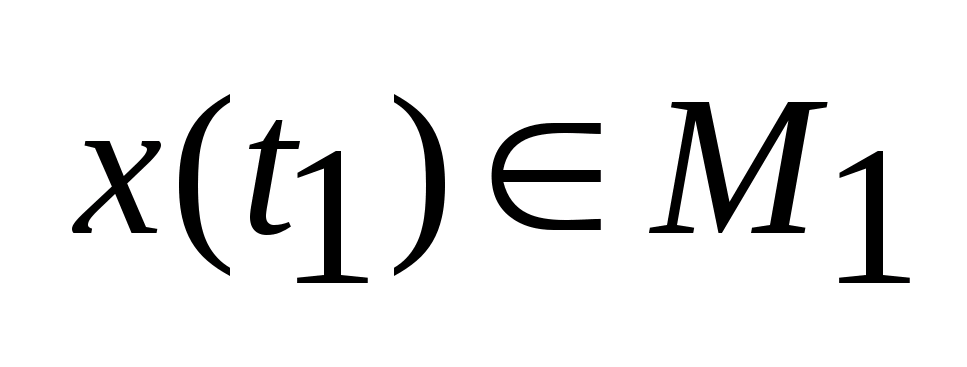 .
Цель управления- перевод динамический
объекта из
.
Цель управления- перевод динамический
объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача быстродействия заключается в
нахождении такого допустимого управления,
которое осуществляет переход из множества
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача быстродействия заключается в
нахождении такого допустимого управления,
которое осуществляет переход из множества
 в
в
 за
наименьшее время.
за
наименьшее время.
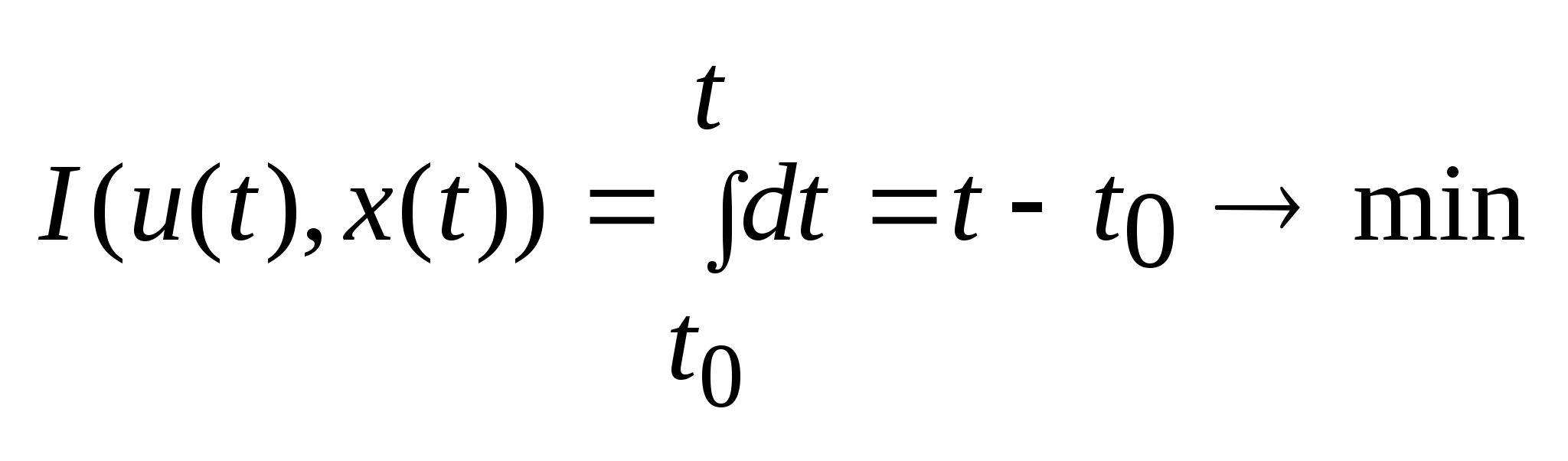 (4).
(4).
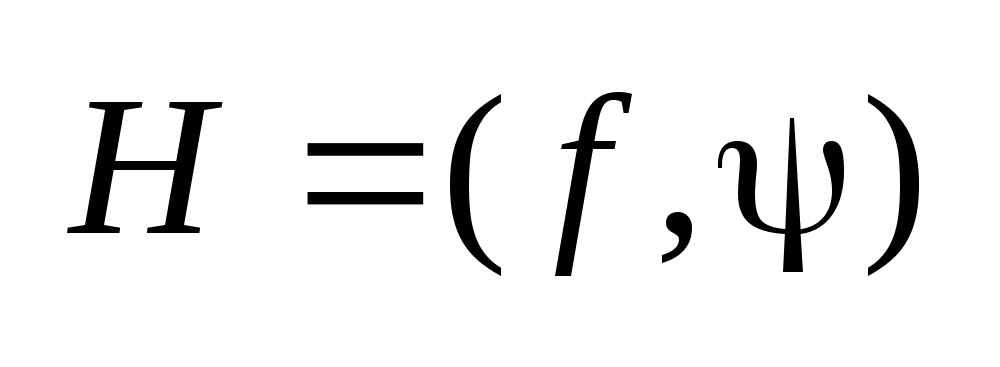 ,
где
,
где
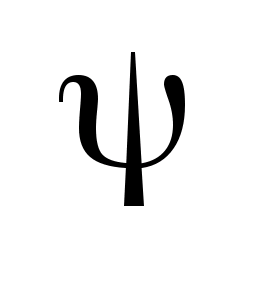 -ненулевая
вектор-функция.
-ненулевая
вектор-функция.
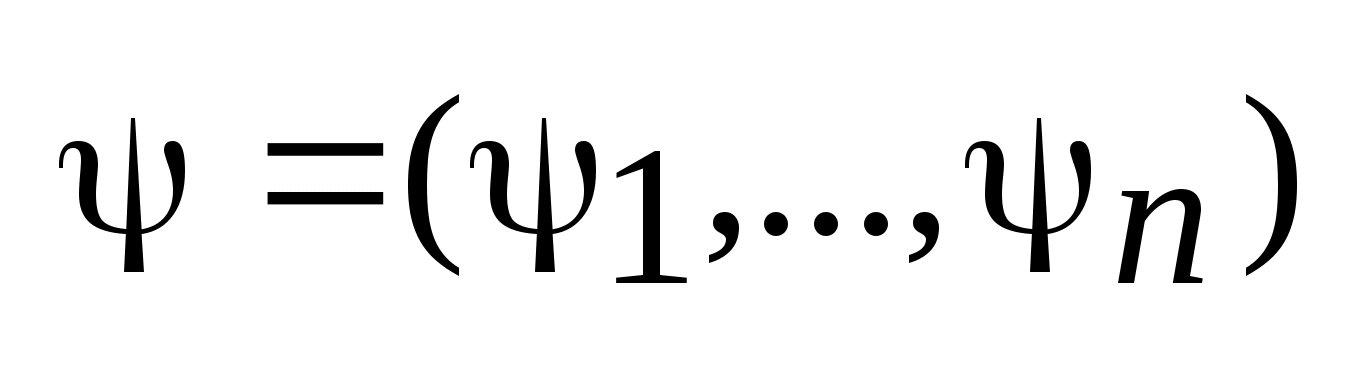 ,
,
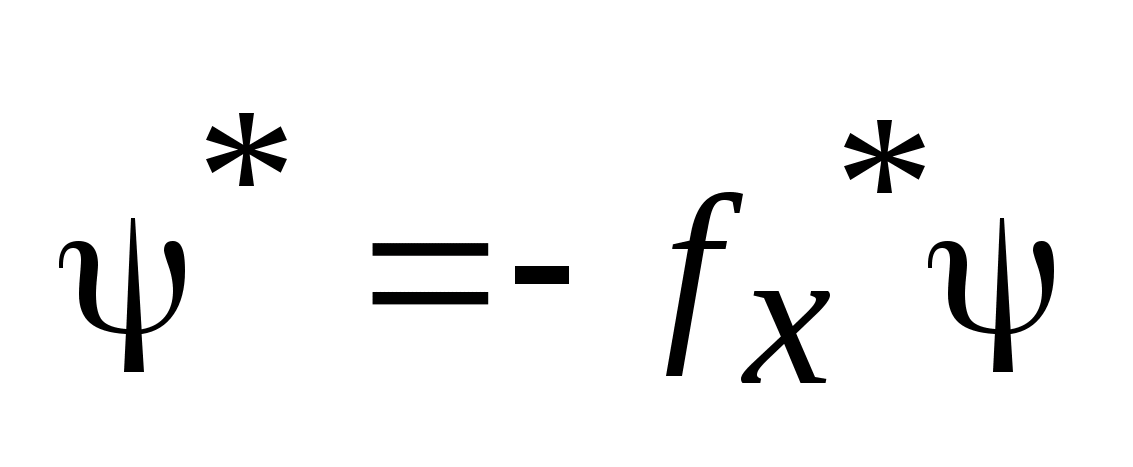 .
Если
.
Если
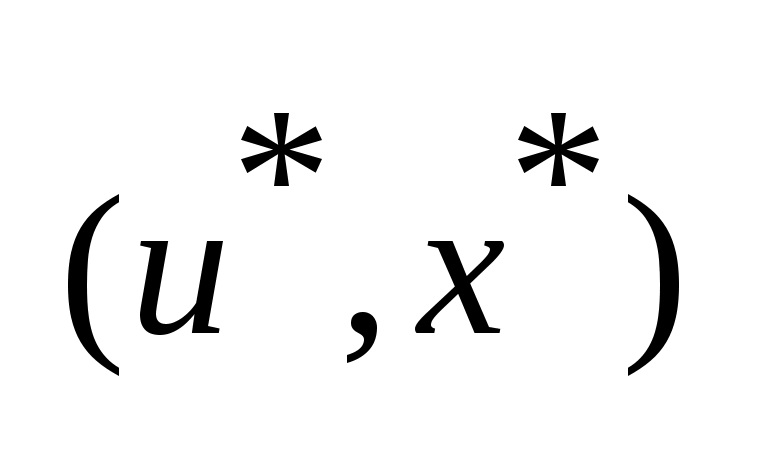 -оптимальное
управление, переводящее
-оптимальное
управление, переводящее
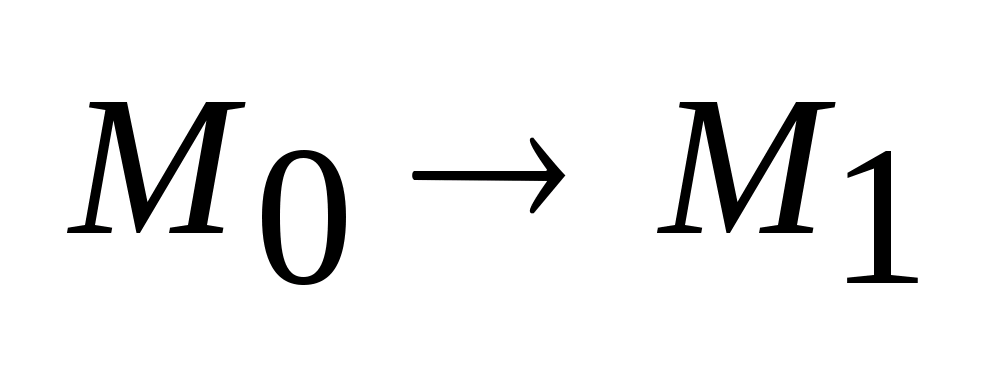 ,
то
,
то
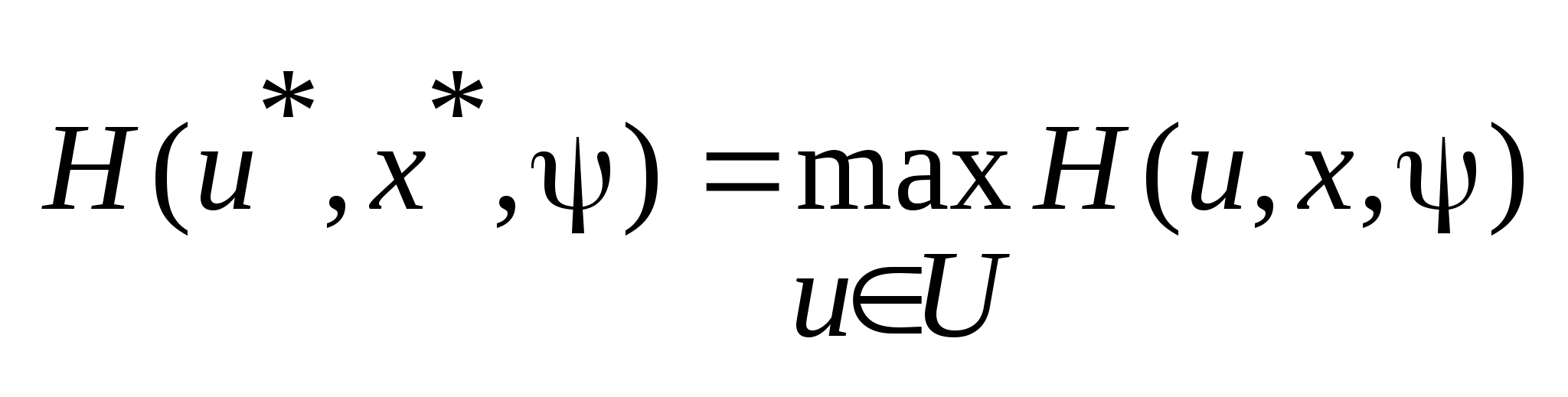 .
.
Для
нашей задачи
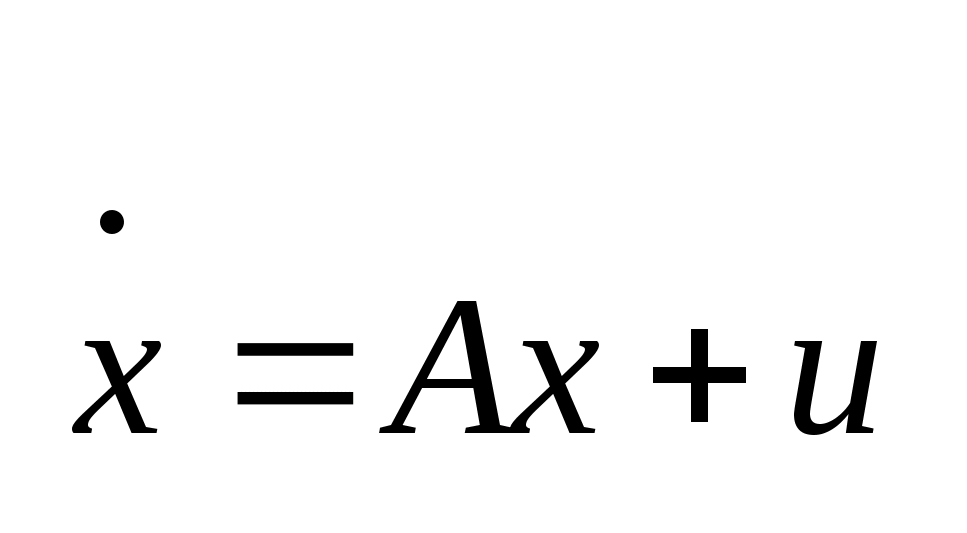 :
:
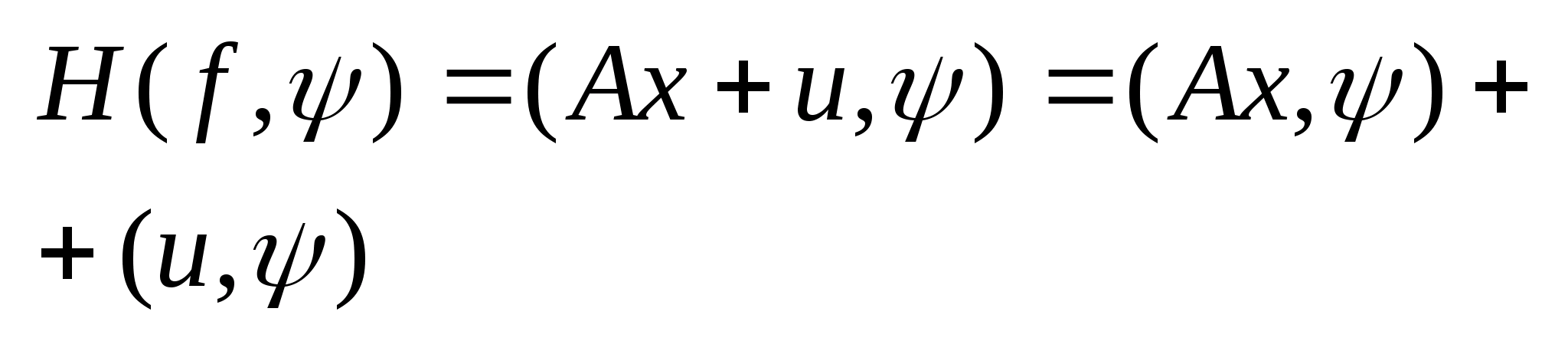 .
.
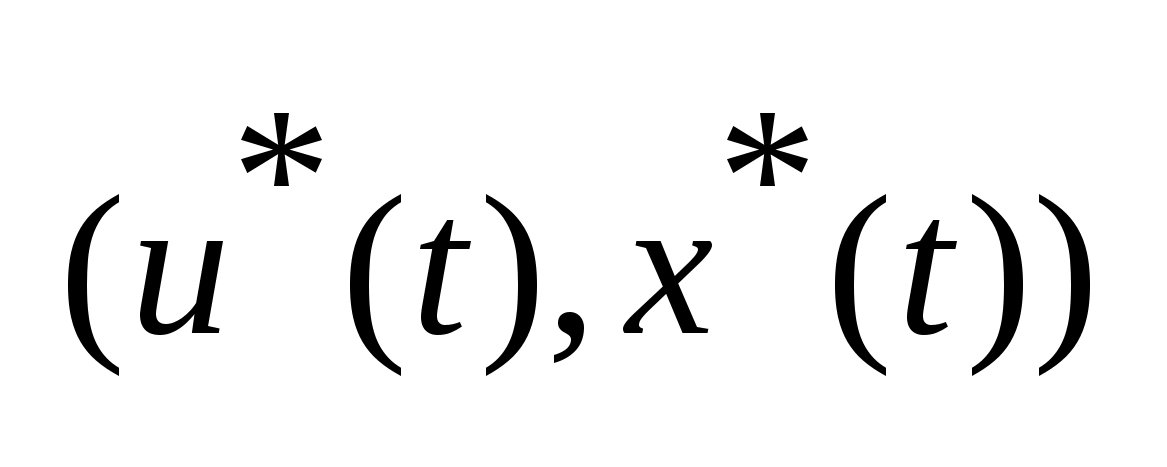 удовлетворяет
принципу максимума Понтрягина на
удовлетворяет
принципу максимума Понтрягина на
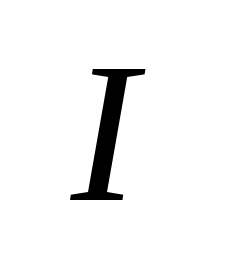 ,
если существует не нулевая вектор
-функция.
,
если существует не нулевая вектор
-функция.
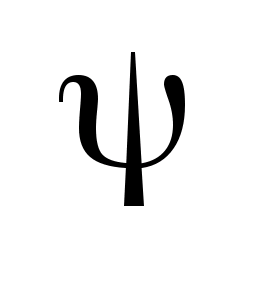 ,
удовлетворяющая системе
,
удовлетворяющая системе
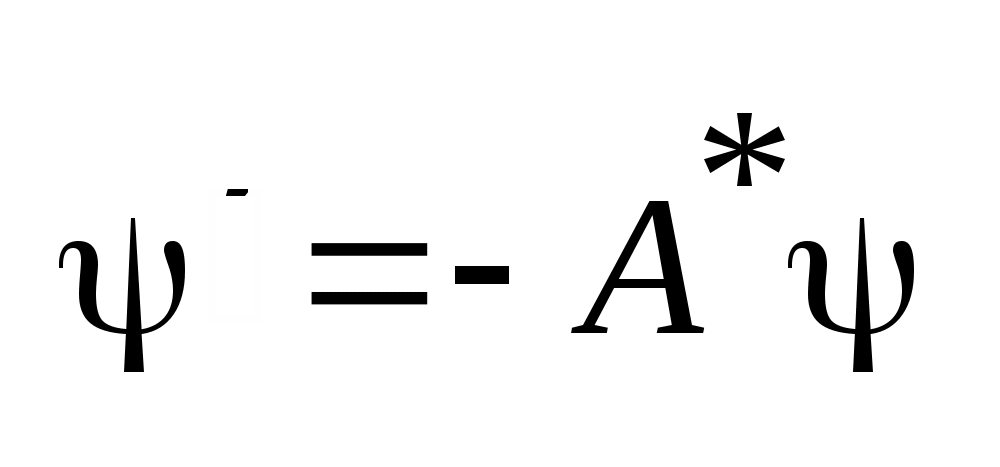 с
нач. условием
с
нач. условием
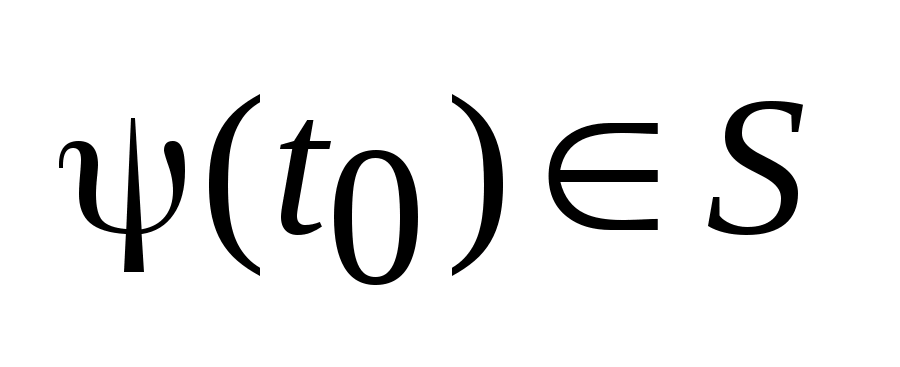 ,
такая что выполняется условие:
,
такая что выполняется условие:
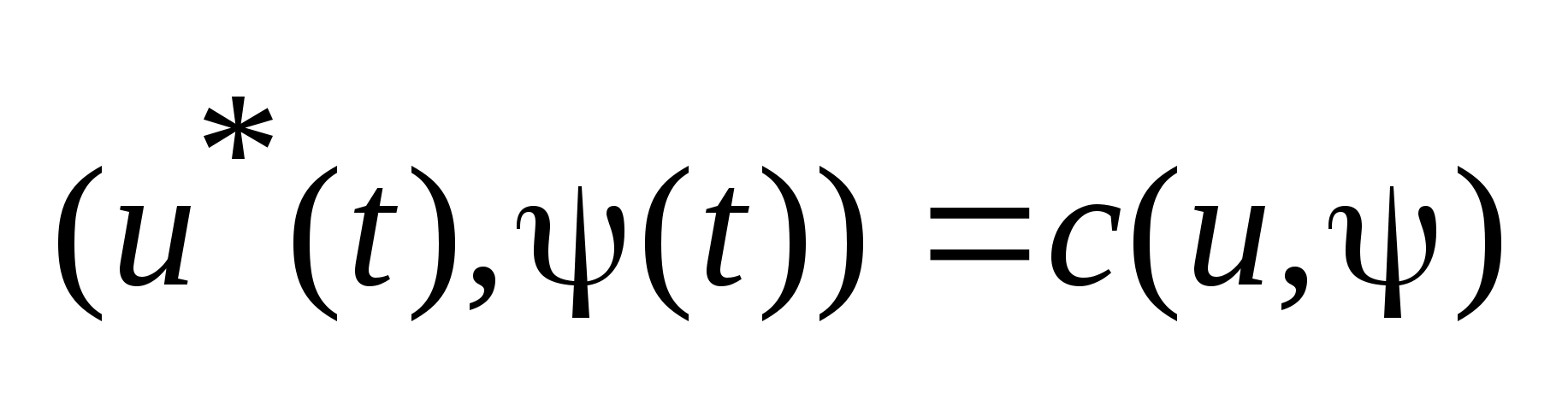 -здесь
достигается максимум.
-здесь
достигается максимум.
2)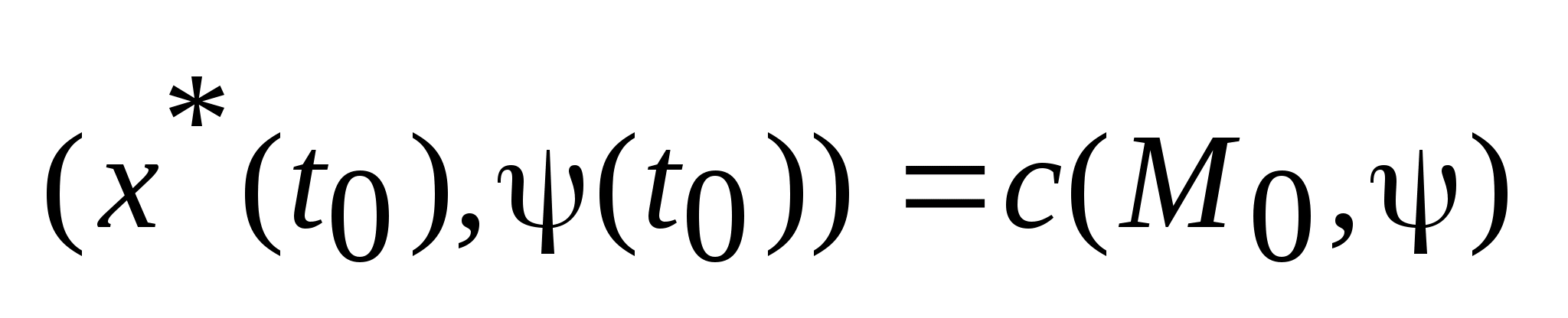 ;
;
3)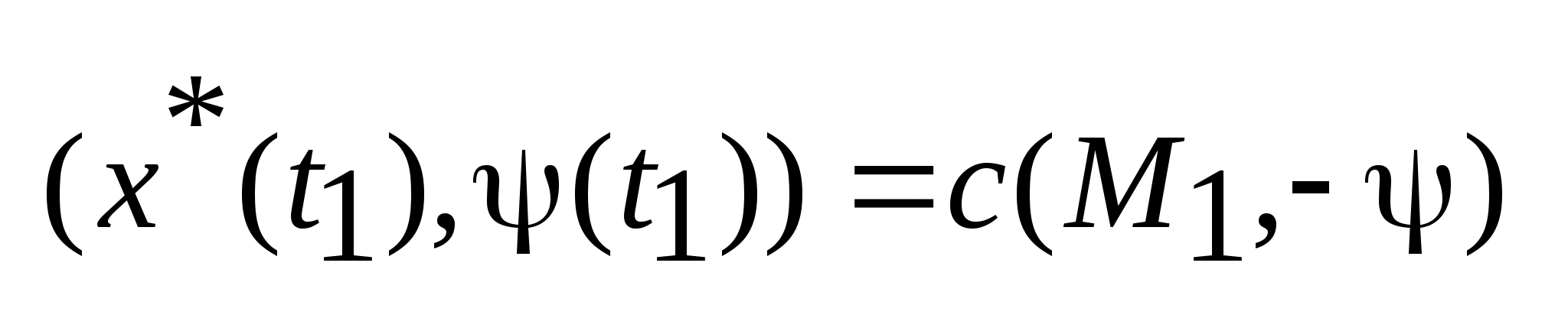 .
.
Теорема
о необходимых условиях оптимальности.
Если в линейной задаче быстродействия
мн-ва
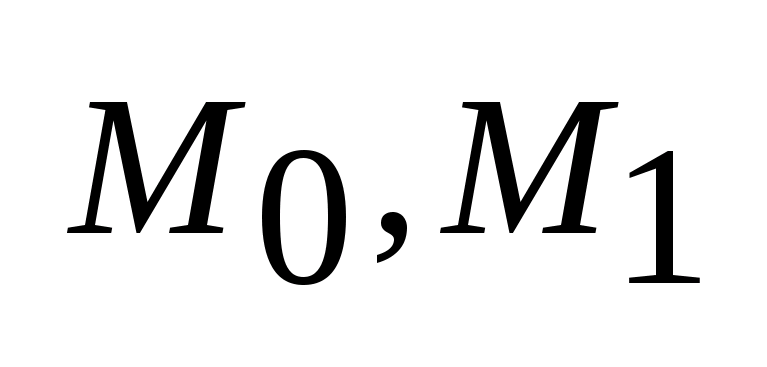 выпуклы,
выпуклы,
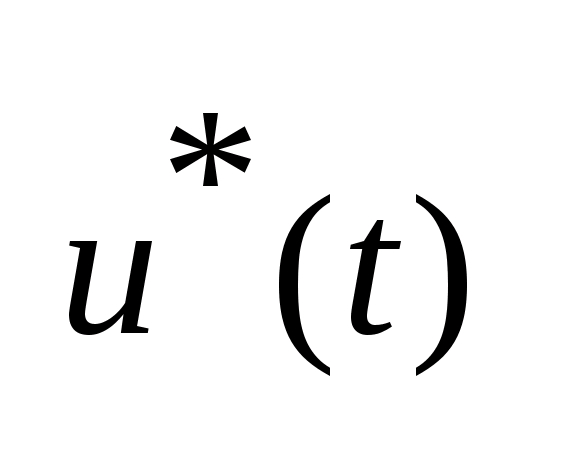 -оптимальное
управление, переводящее
-оптимальное
управление, переводящее
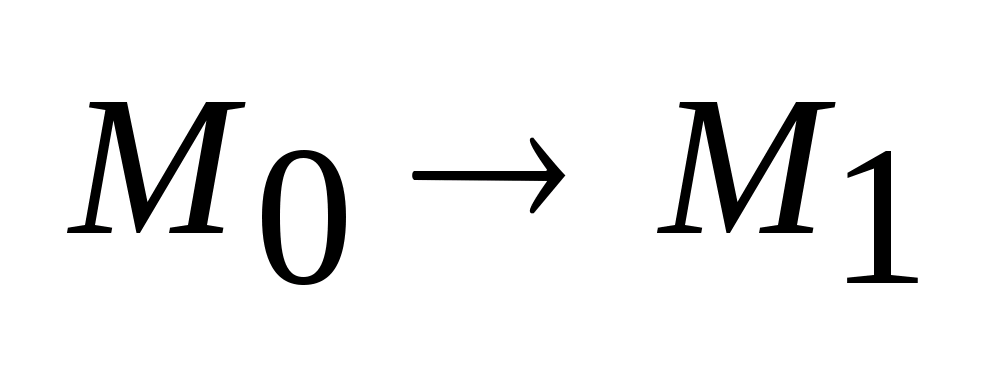 на
отр.
на
отр.
 ,
а
,
а
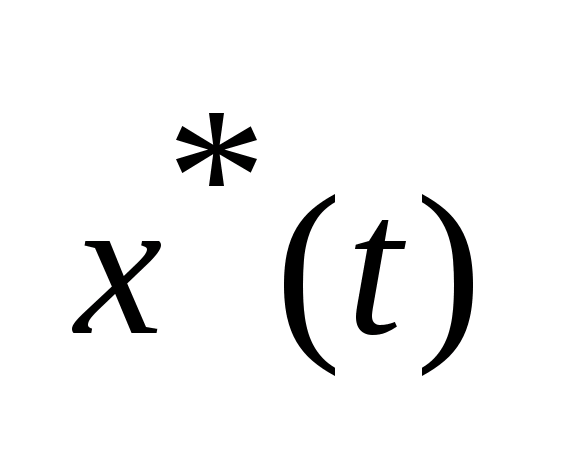 -соответствующая
траектория, то пара
-соответствующая
траектория, то пара
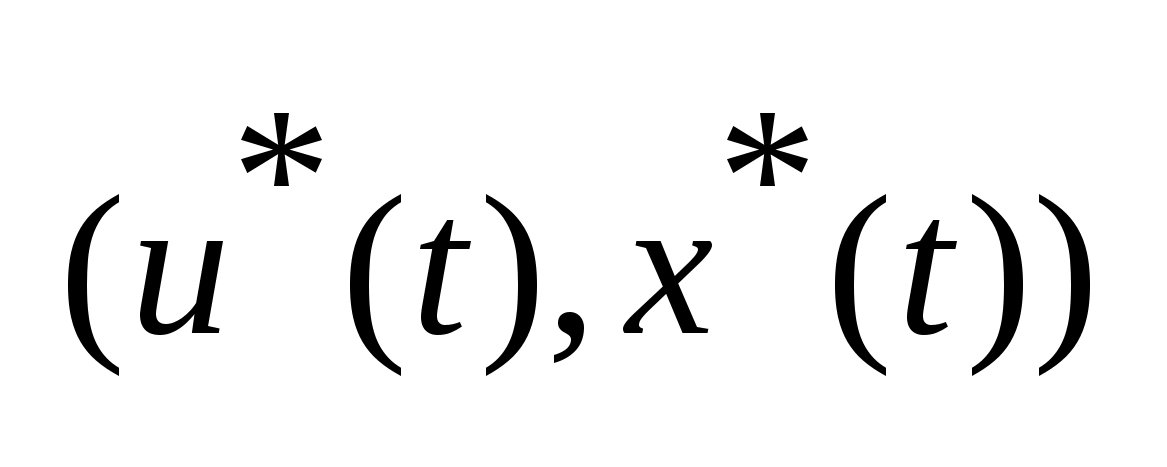 удовлетворяет
принципу максимума Понтрягина.
удовлетворяет
принципу максимума Понтрягина.
23. Применение необходимых условий оптимальности(схема и пояснения к ней).
Рассматриваем
динамический объект, поведение которого
описывается системой (1)
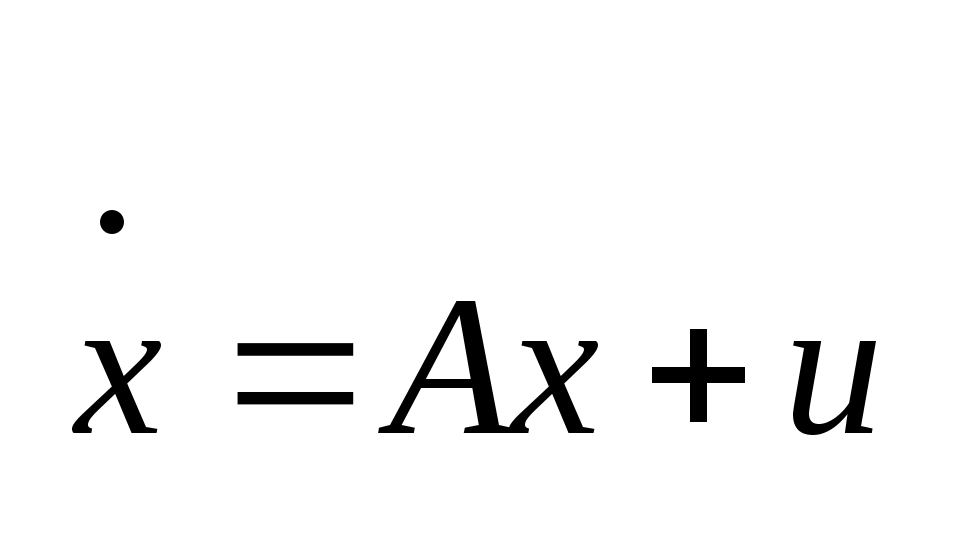 ,
x-
n-мерный
вектор,
,
x-
n-мерный
вектор,
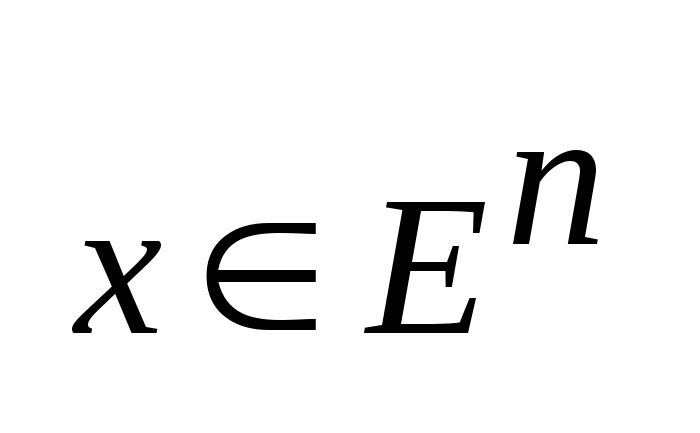 ,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
,
A-матрица
nxn,
u
имеет ту же размерность,
что
и
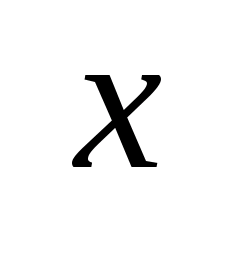 ,
,
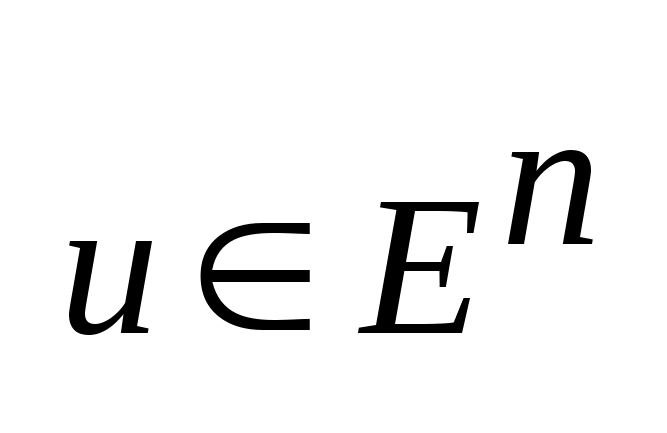 .Задано
.Задано
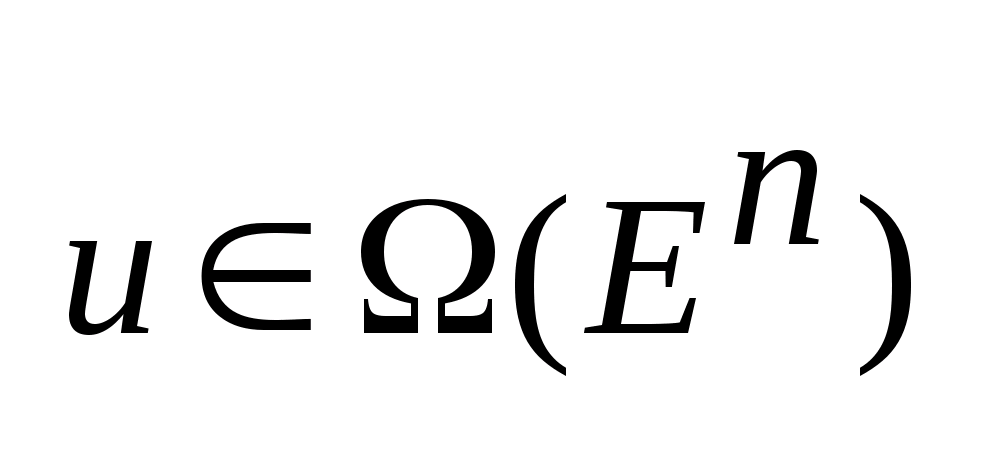 ,
u:
I
,
u:
I
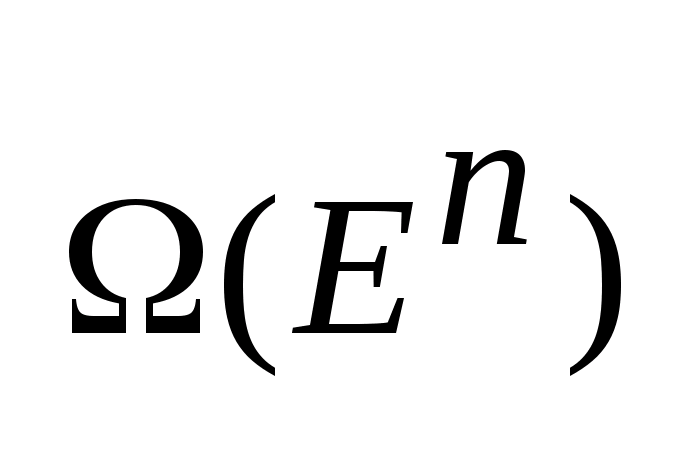 и полагается, что u(t)
измеримо
и
и полагается, что u(t)
измеримо
и
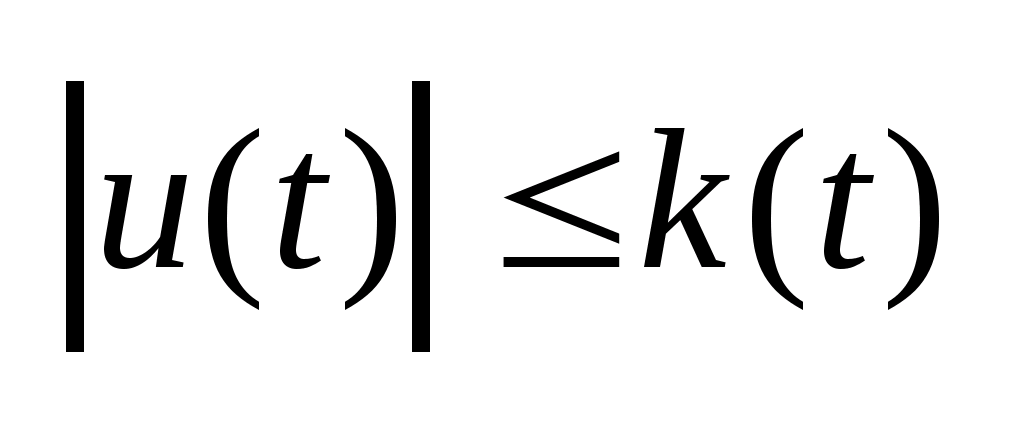 -
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью из многозначного отображения
U
u(t)
-
где
k(t)
скалярная функция интегрируемая
по Лебегу на отрезке I .Функция
u(t)-
называется допустимым управлением,
если измерима и является однозначной
ветвью из многозначного отображения
U
u(t)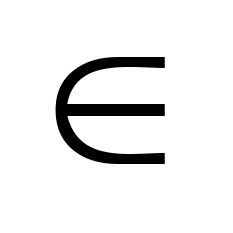 U(t)
-
ограничения на управления . В фазовом
пространстве
U(t)
-
ограничения на управления . В фазовом
пространстве
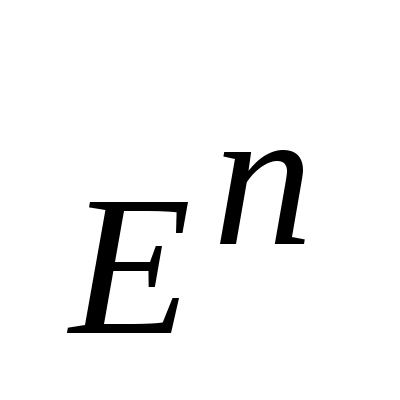 заданы
два не пустых множества
заданы
два не пустых множества
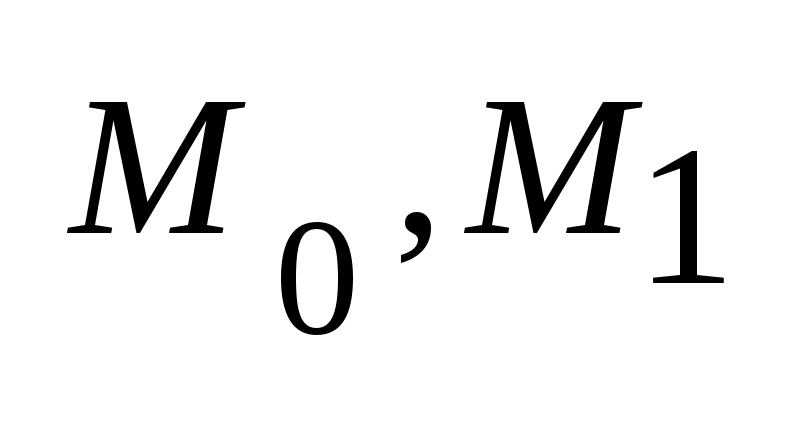
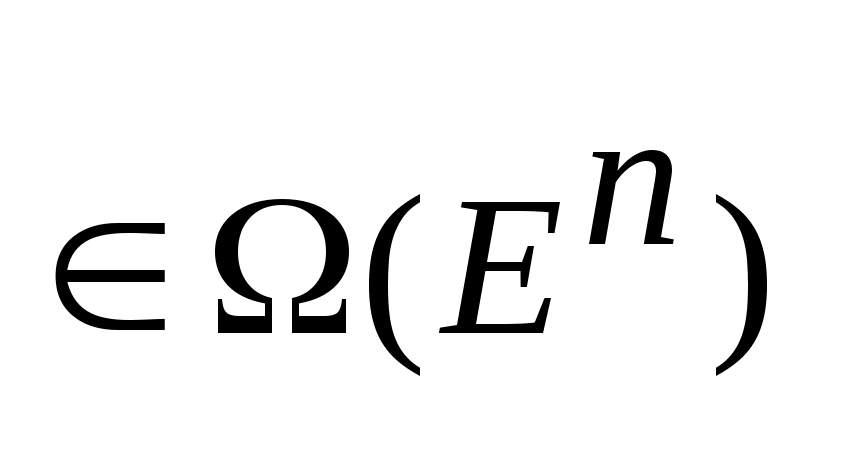 ,
,
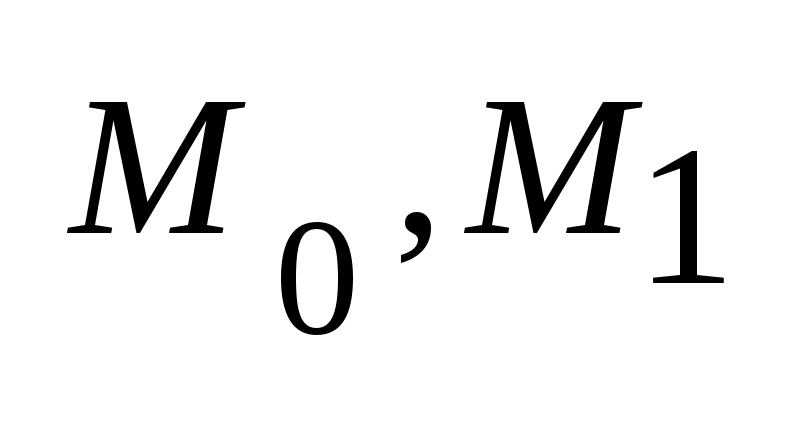 -выпуклы.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
-выпуклы.
Допустимое управление u(t)
на отр.I
осуществляете
переход из начального мн-ва
 в конечное множество
в конечное множество
 ,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
,
если существует решение уравнения (1),
удовлетворяющее граничным условиям
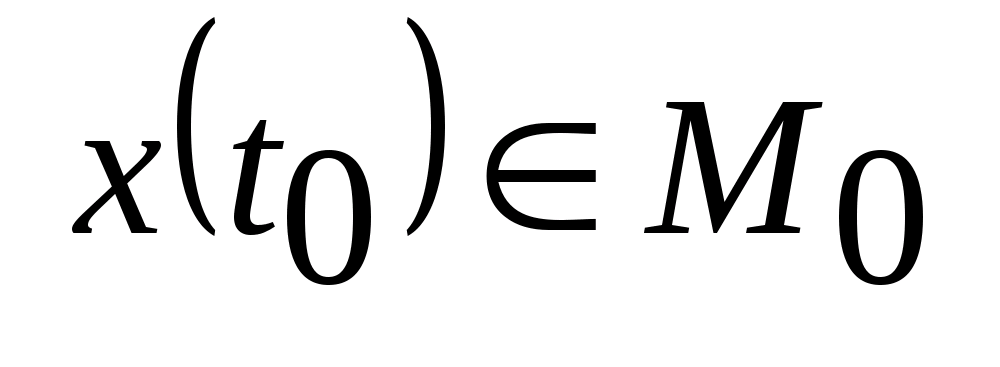 и
и
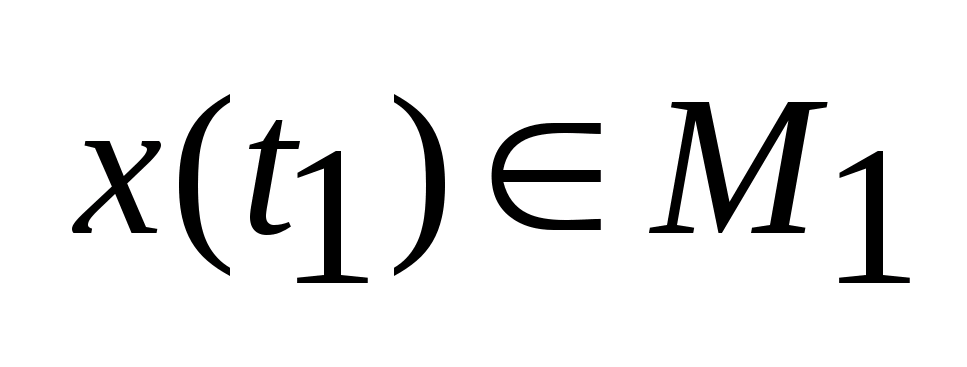 .
Цель управления- перевод динамический
объекта из
.
Цель управления- перевод динамический
объекта из
 в
в
 ,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
,
а качество определяет функционал. Таким
функционалом явл. время, следовательно
задача быстродействия заключается в нахождении такого допустимого управления, которое осуществляет переход из
множества
 в
в
 за
наименьшее время.
за
наименьшее время.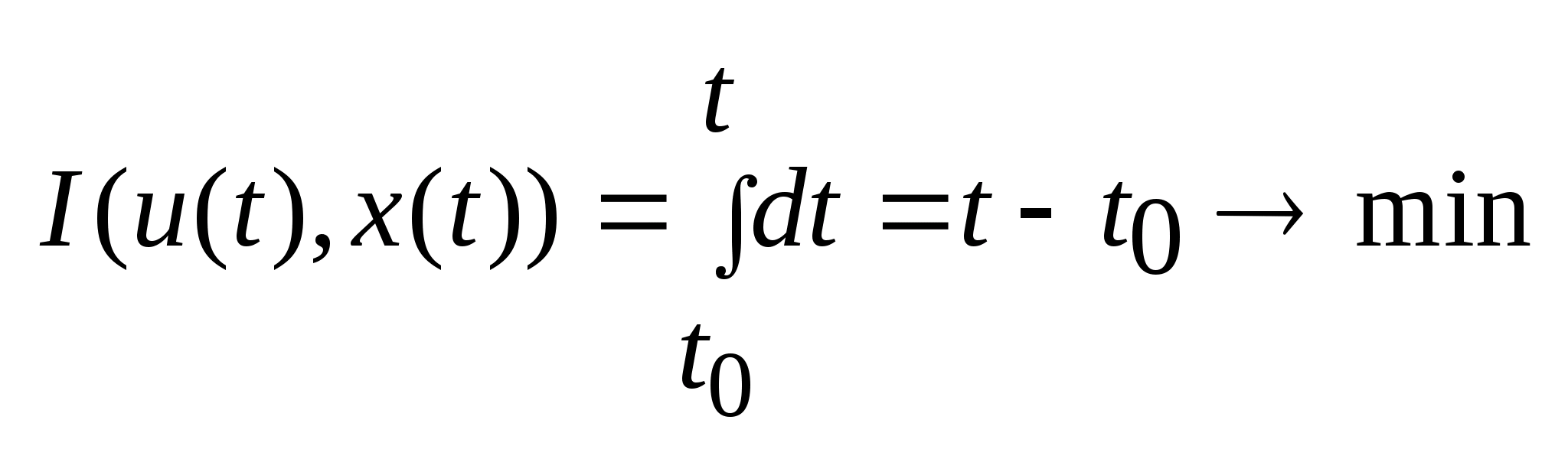 .
.
Пусть
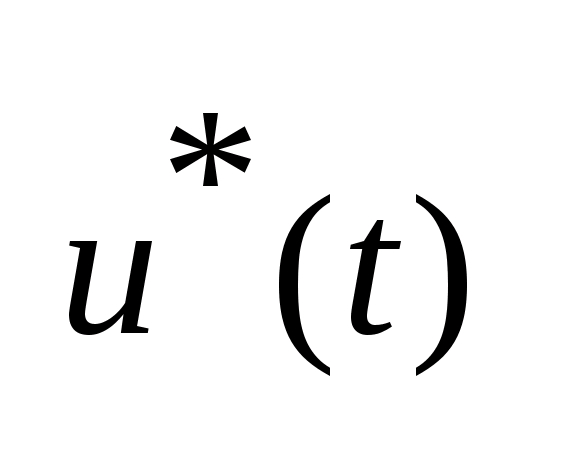 оптимальное
управление,
оптимальное
управление,
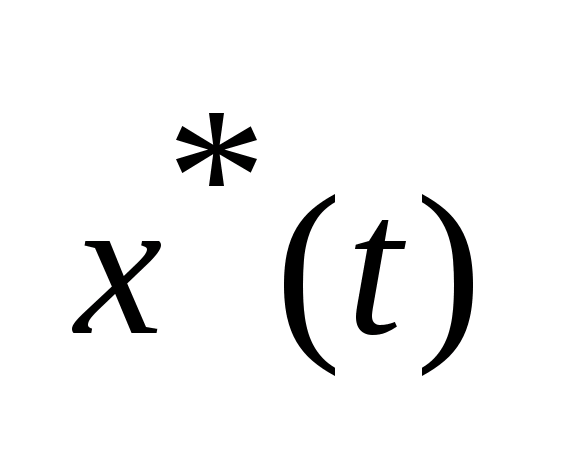 -соответствующая
траектория, переводящая
-соответствующая
траектория, переводящая
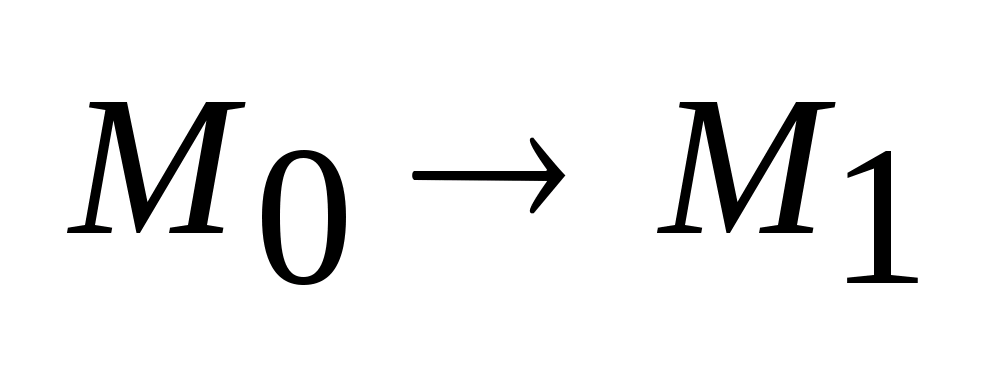 за
время I
. И
за
время I
. И
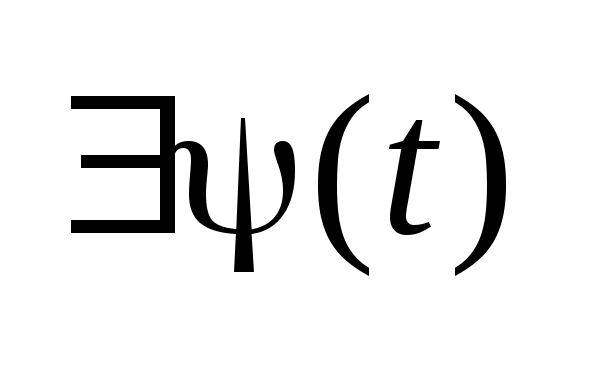 -
ненулевая функция, такая что
-
ненулевая функция, такая что
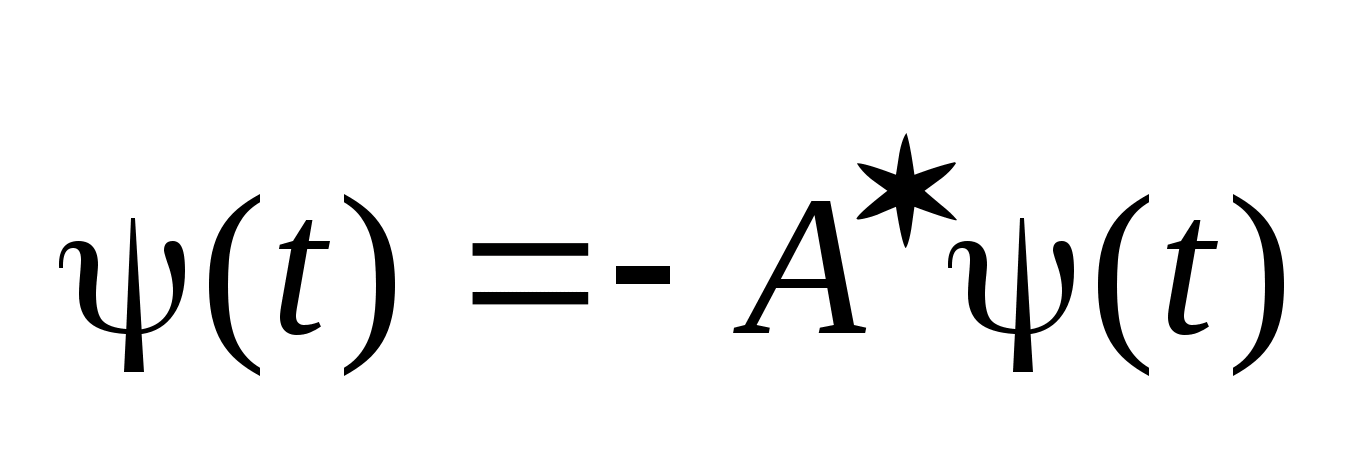 (2).
(2).
1)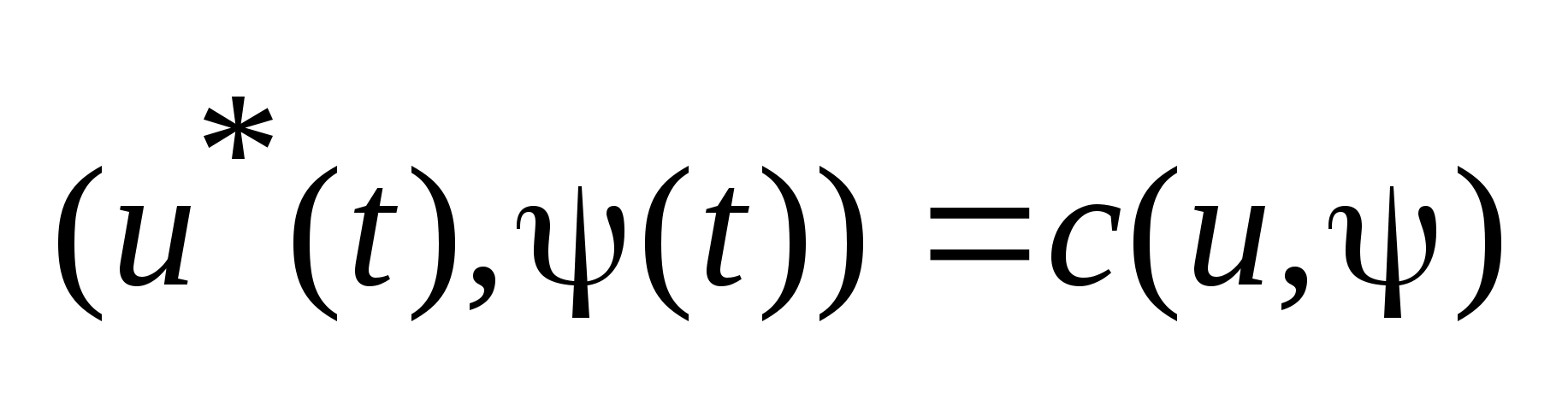 (3);
(3);
2) (4);
(4);
3)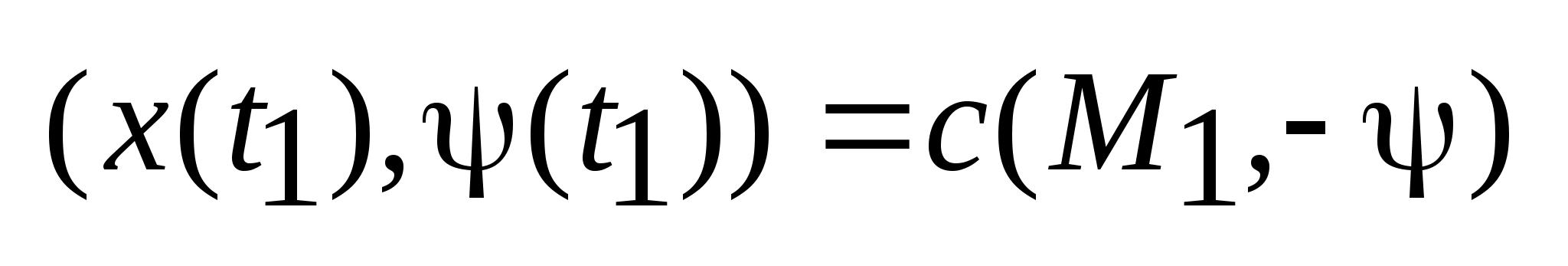 (5)
(5)
Найти
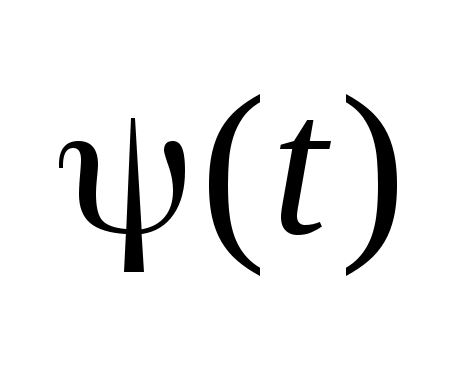 :
:
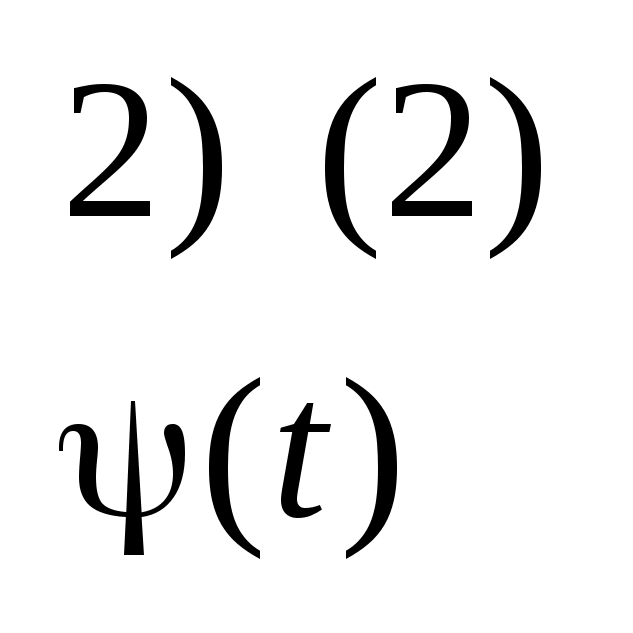

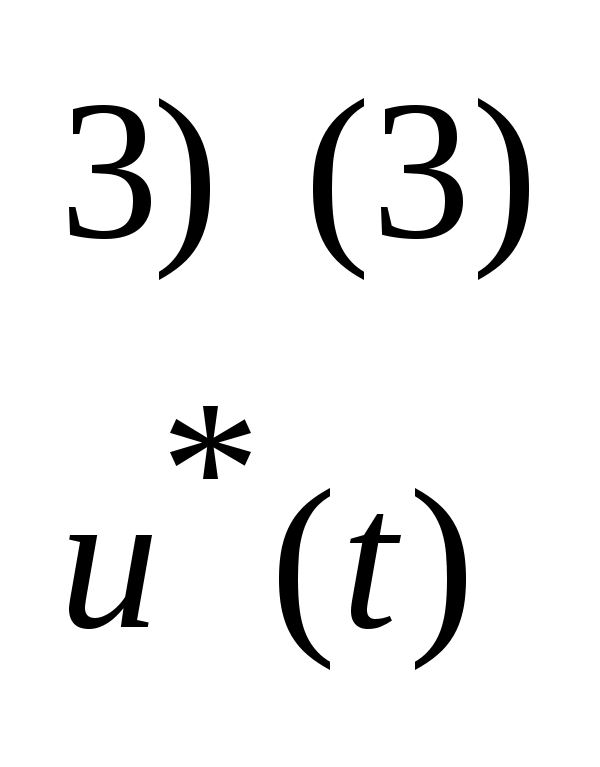
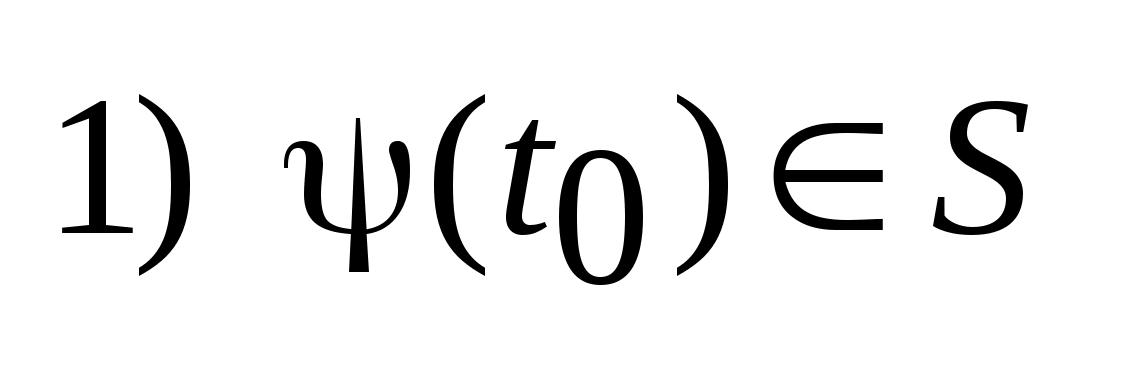
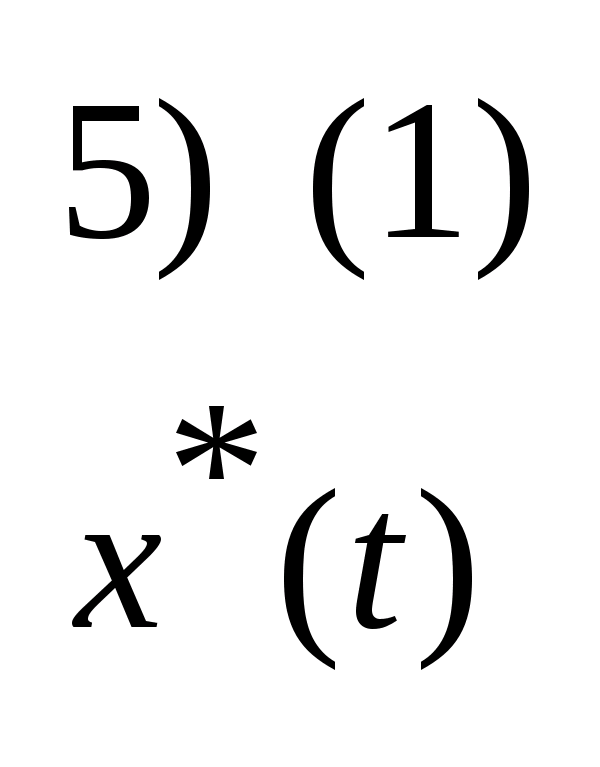
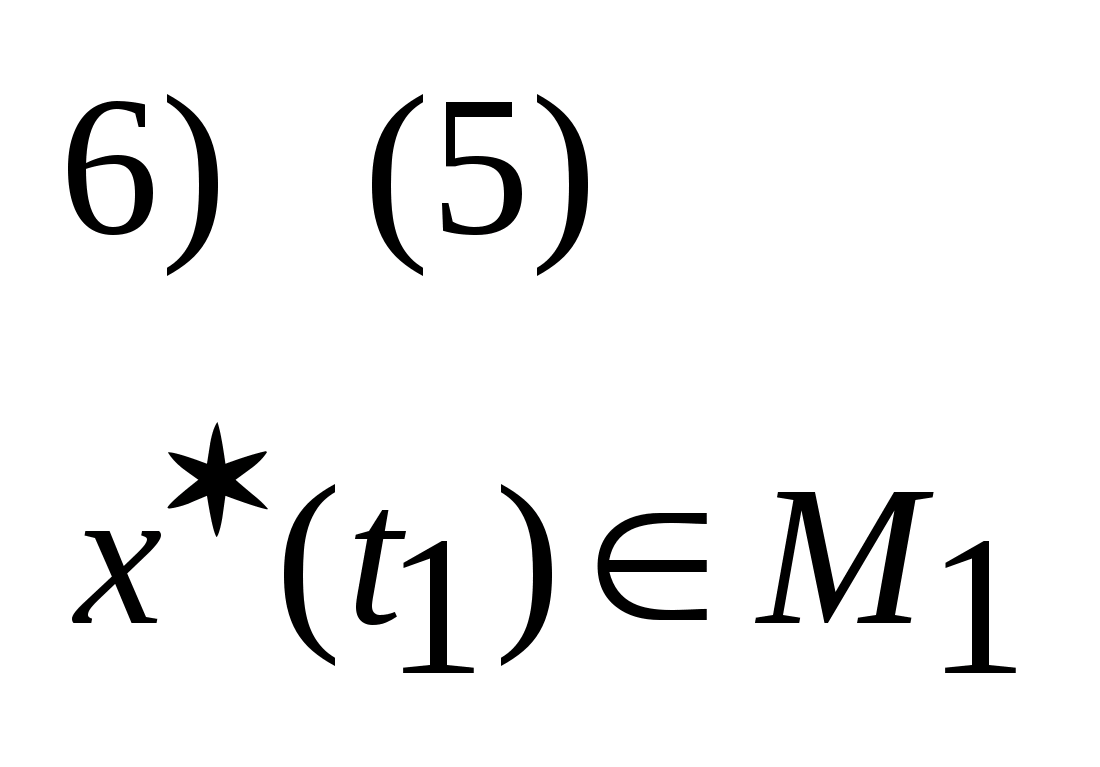
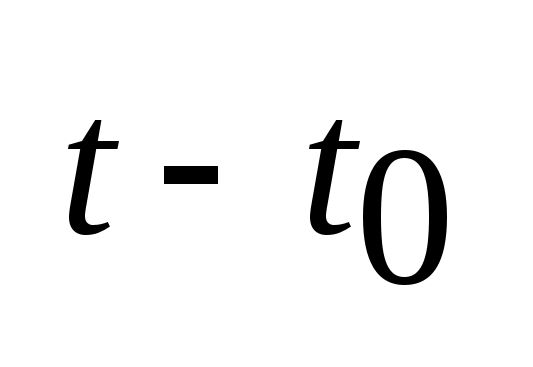
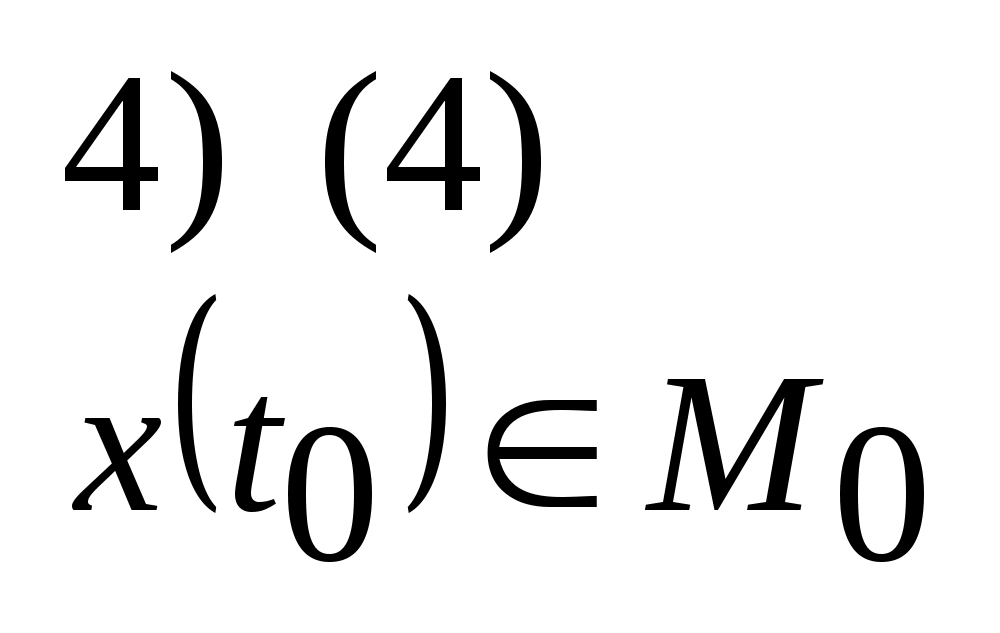
24. Достаточное условие оптимальности.
( Вначале написать вопрос «Применение необходимых условий оптимальности(схема и пояснения к ней»)
Для
линейной задачи существует дост. условие.
Для этого необходимо выполнение
дополнительных условий: усиление условия
трансверсальности 4) решение
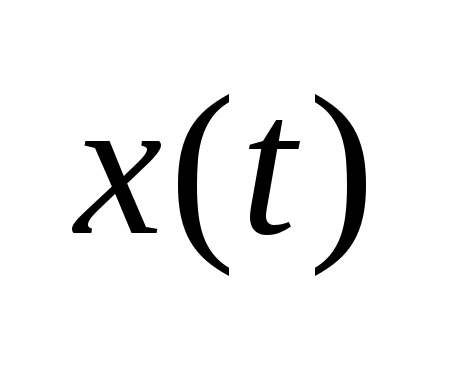 удовлетворяет
усиленному условию трансверсальности
на
удовлетворяет
усиленному условию трансверсальности
на
 на
отр.
на
отр.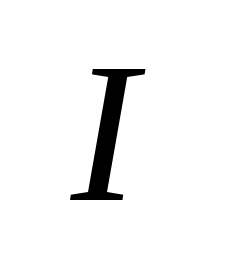 ,
если для
,
если для
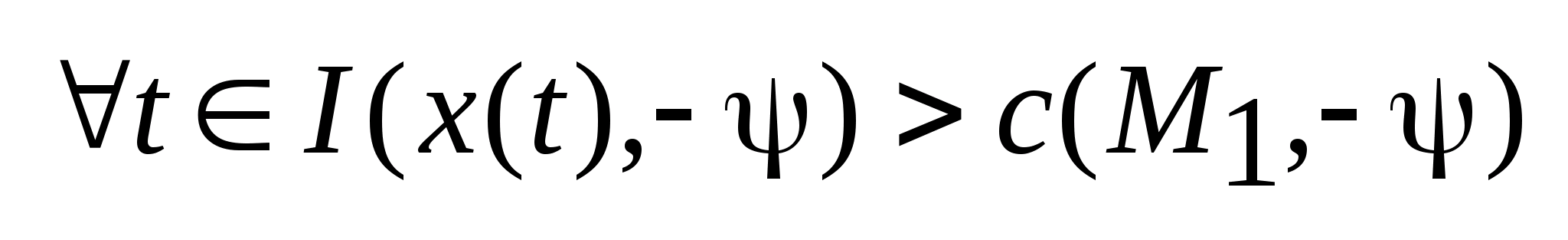 (6).
(6).
Достаточное
условие: если
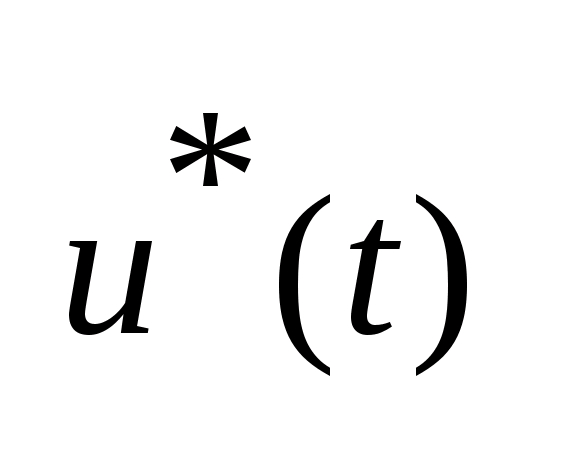 допустимое
управление,
допустимое
управление,
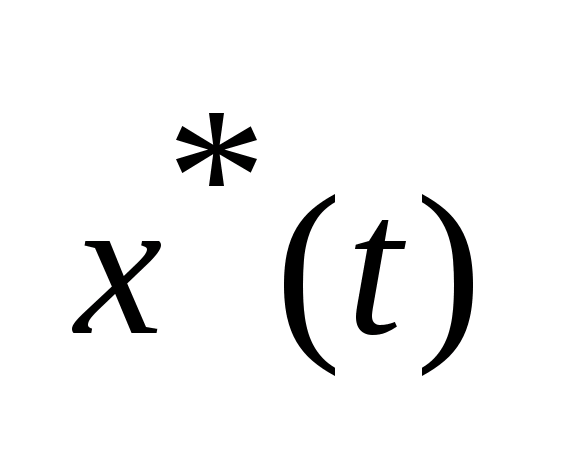 -соответствующая
траектория, переводящая
-соответствующая
траектория, переводящая
 за
время I
и пара
за
время I
и пара
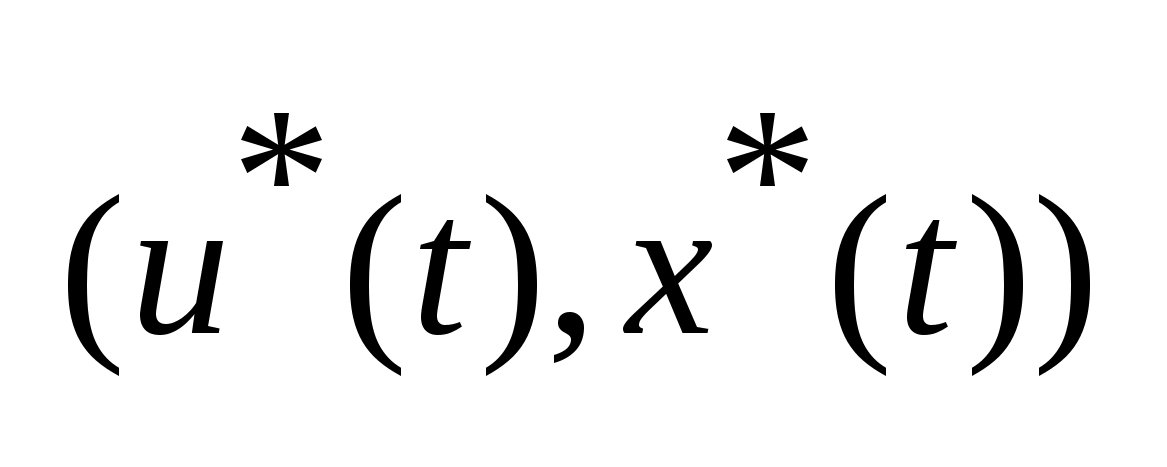 удовлетворяет
принципу максимума Понтрягина (2-5) и
усиленному условию трансверсальности
(6), то
удовлетворяет
принципу максимума Понтрягина (2-5) и
усиленному условию трансверсальности
(6), то
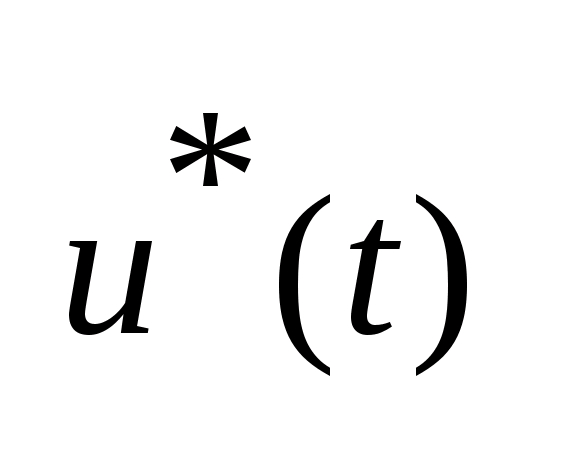 -
оптимальное управление.
-
оптимальное управление.
Следствие
из теоремы достаточного условия
трансверсальности. Используем локальную
управляемость:
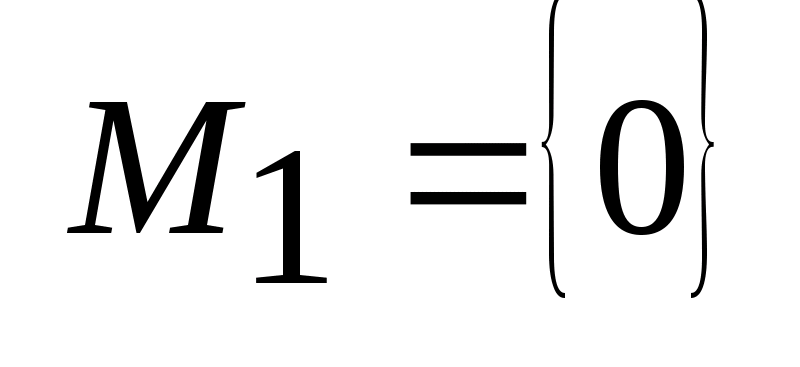 .Если
.Если
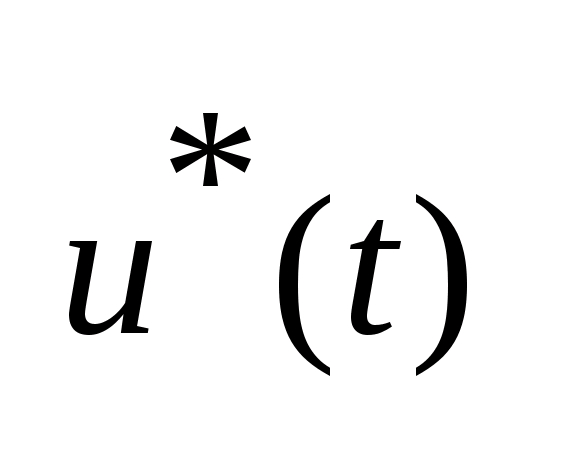 некоторое
допустимое управление, а
некоторое
допустимое управление, а
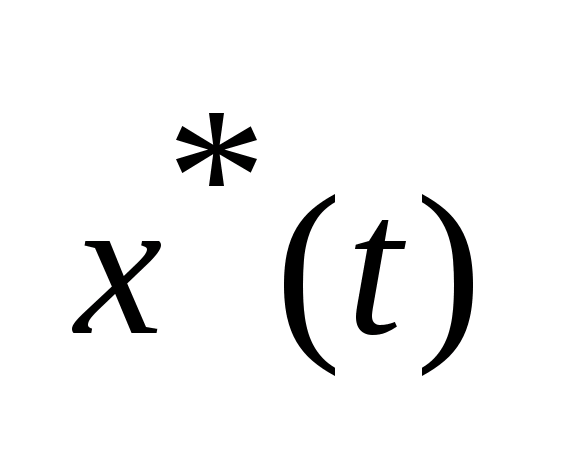 -
соответствующее решение (1), переводящее
-
соответствующее решение (1), переводящее
 за время I,
удовлетворяет
принципу максимума Понтрягина и объект
явл. локально управляемым в т.0 на любом
отр.
за время I,
удовлетворяет
принципу максимума Понтрягина и объект
явл. локально управляемым в т.0 на любом
отр.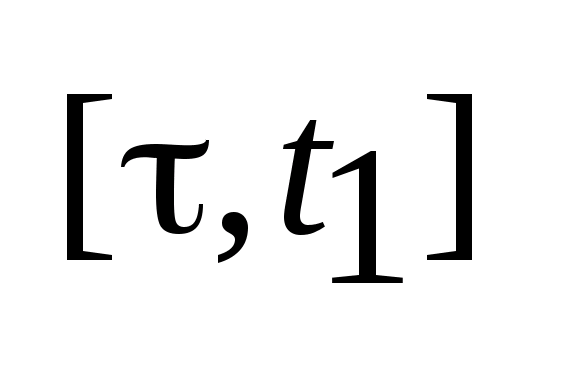 ,
то управление
,
то управление
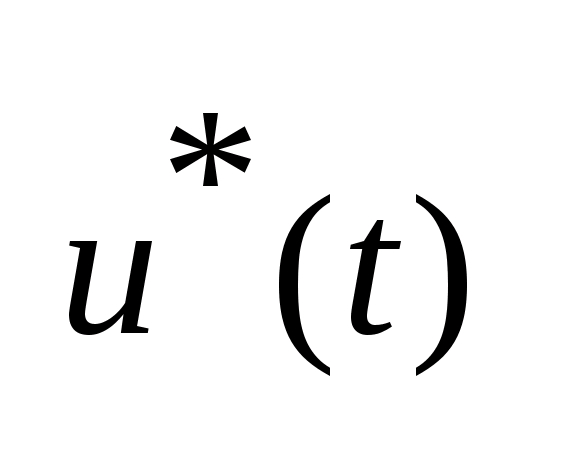 -
оптимально.
-
оптимально.
25. Единственность оптимального управления для линейной задачи.
( В начале написать вопрос «Применение необходимых условий оптимальности(схема и пояснения к ней)»)
При
решении с использованием принципа
максимума Понтрягина в пунктах 3,4
нарушается единственность. При выборе
 из
условия 4 и выборе
из
условия 4 и выборе
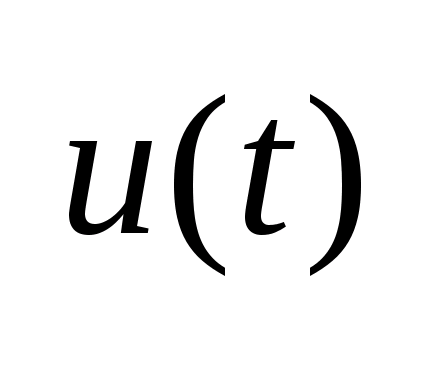 из условия (3). Пусть задана
из условия (3). Пусть задана
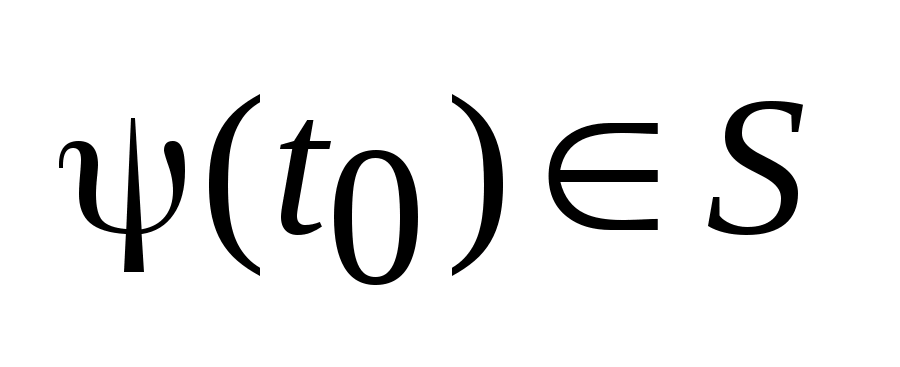 и
сопряженная функция
и
сопряженная функция
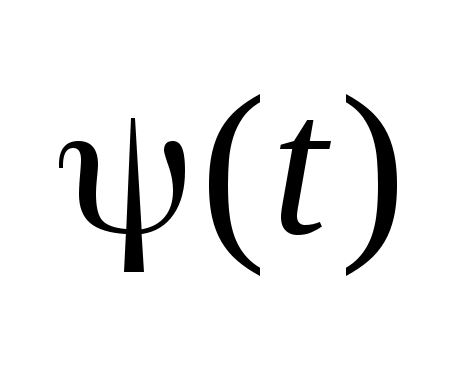 удовлетворяющая
системе (2), если опорная функция
удовлетворяющая
системе (2), если опорная функция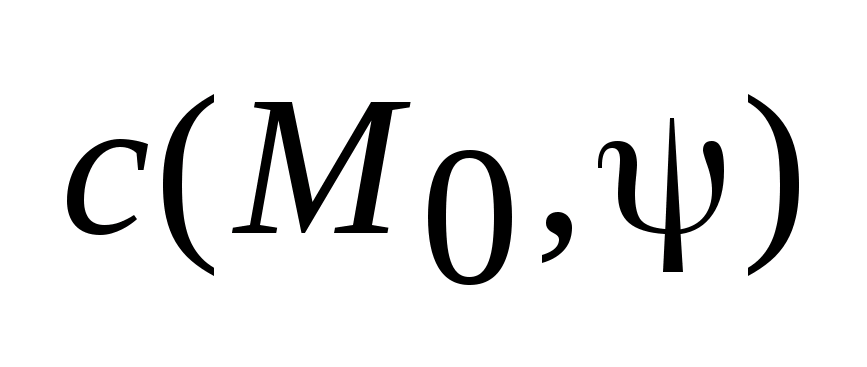 является
дифференцируемой по
является
дифференцируемой по
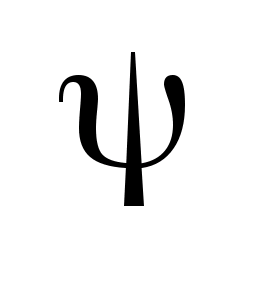 в точке
в точке
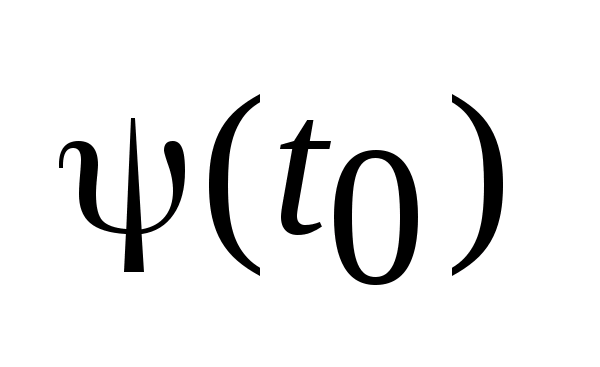 ,
т.е. в этой точке существует градиент
функции
,
т.е. в этой точке существует градиент
функции
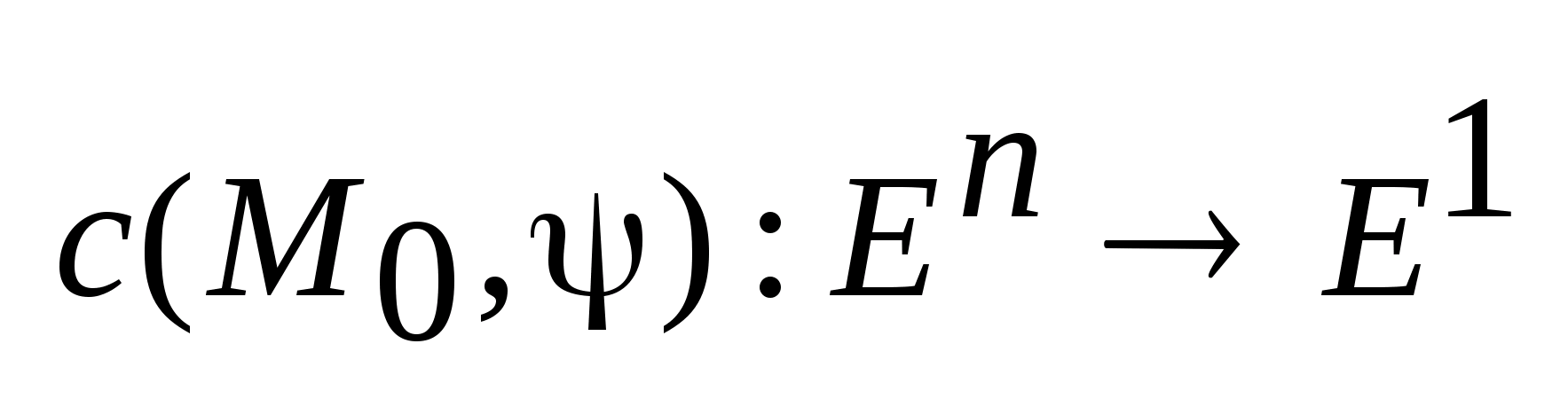 и
для почти всех
и
для почти всех
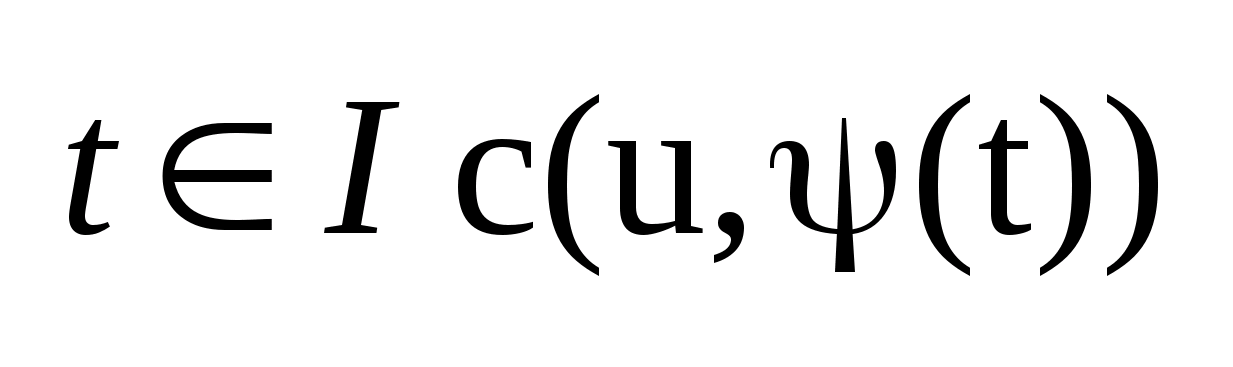 дифференцируемая по
дифференцируемая по
 ,
то соответствующая пара
,
то соответствующая пара
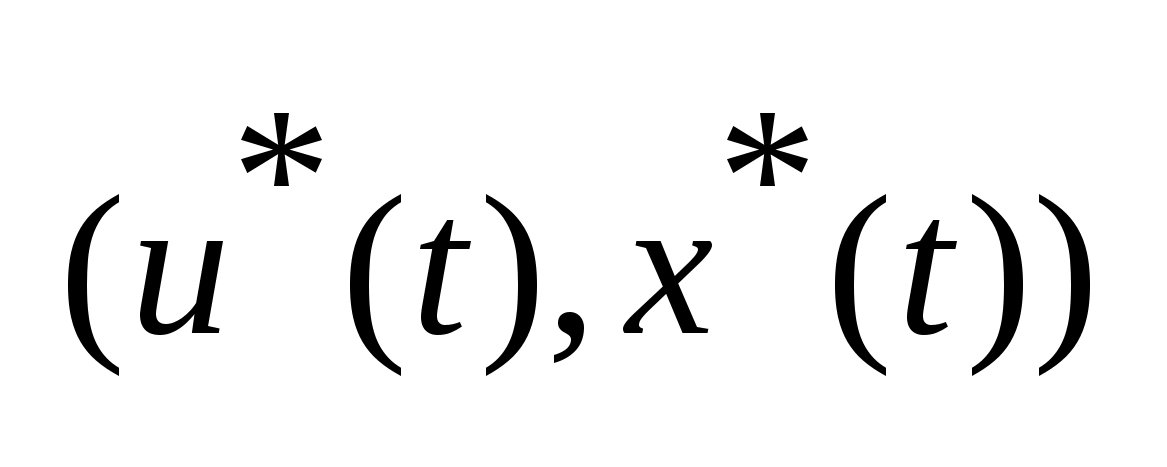 ,
удовлетворяющая принципу максимума
Понтрягина, является единственной.
,
удовлетворяющая принципу максимума
Понтрягина, является единственной.
Следствие:
Если мн-во
 и
и
 строго выпуклы для почти всех t
, принадлежащих I,
тогда для любого начального значения
строго выпуклы для почти всех t
, принадлежащих I,
тогда для любого начального значения
 ,
соответствующая пара
,
соответствующая пара
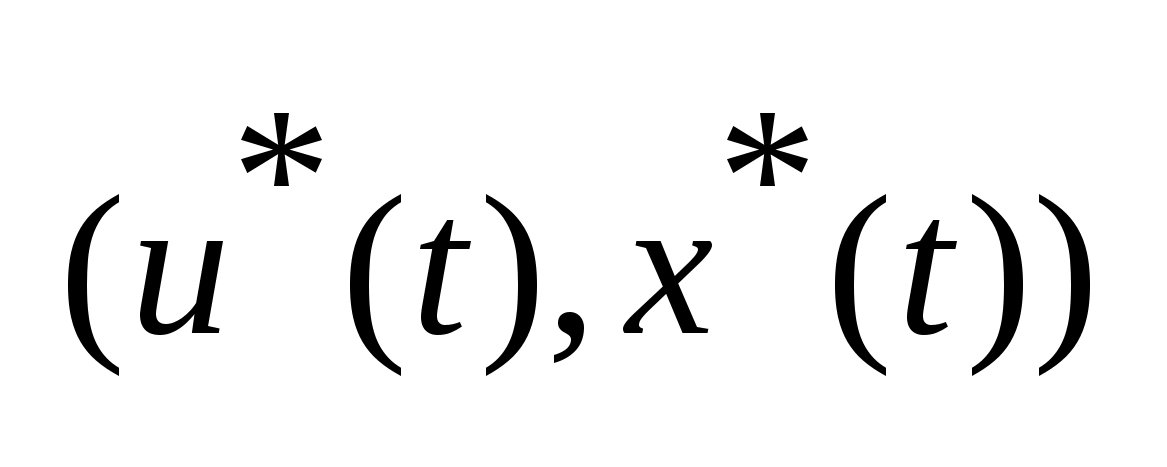 ,
удовлетворяющая принципу максимума
Понтрягина, является единственной.
,
удовлетворяющая принципу максимума
Понтрягина, является единственной.
|
1. Общая постановка задачи управляемости. 2. Основные вопросы в теории ОУ. 3. Постановка линейной задачи.
4.
Пространство
5. 6.Опорные функции. 7.Свойства опорной функции. 8. Непрерывные функции. Условия Липшица. Лемма 1,2 об условиях Липшица для опорных функций. 9. Многозначные отображения. 10. Непрерывные и равномерно непрерывные многозначные отображения. 11. Измеримые многозначные отображения. Лемма о равномерной непрерывности многозначного отображения. 12. Интеграл от многозначного отображения. Теорема о непрерывности от многозначного отображения. 13.Теоремы 1, 2 о других видах многозначных отображений. 14. Линейная задача быстродействия. Определение абс. непрерывной функции. Теорема Каратеодори.
15.Множество
достижимости и его свойства. 16.Общая задача управляемости. Теорема об управляемости. 17.Численное решение задачи управляемости. 18. Лемма о внутренней точке. 19. Локальная управляемость. Теорема о локальной управляемости.. 20. Теорема о локальной управляемости. (дает достаточное условие локальной управляемости) 21. Теорема о существовании оптимального управления. 22. Принцип максимума Понтрягина на языке опорных функций. 23. Применение необходимых условий оптимальности(схема и пояснения к ней). 24. Достаточное условие оптимальности. 25. Единственность оптимального управления для линейной задачи. |
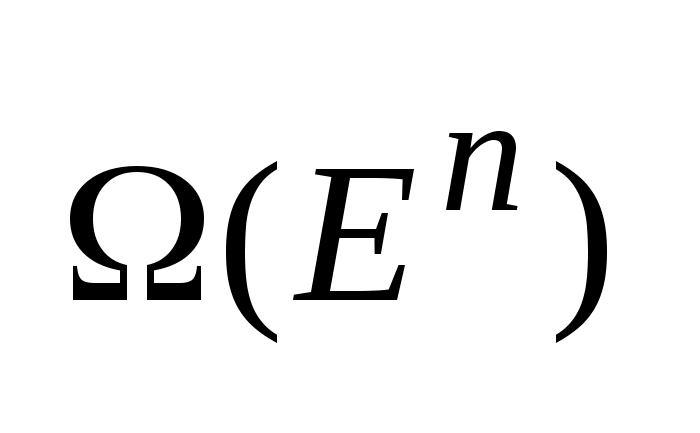 ,
алгебраическая сумма
,
алгебраическая сумма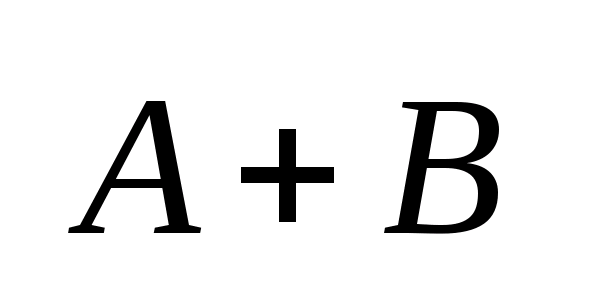 ,
произведение множества на число
,
произведение множества на число
 ,
хаусдорффова норма, лемма про
определенность хаус. нормы.
,
хаусдорффова норма, лемма про
определенность хаус. нормы.