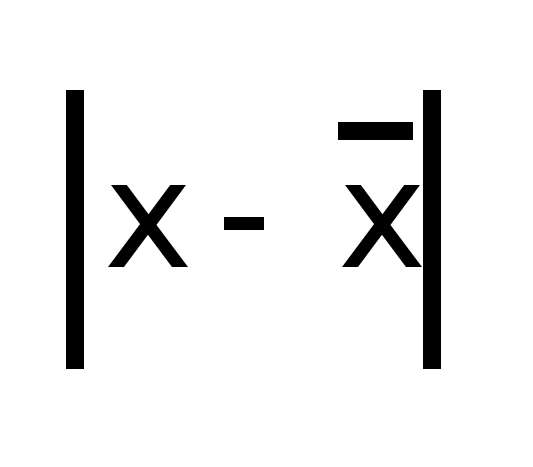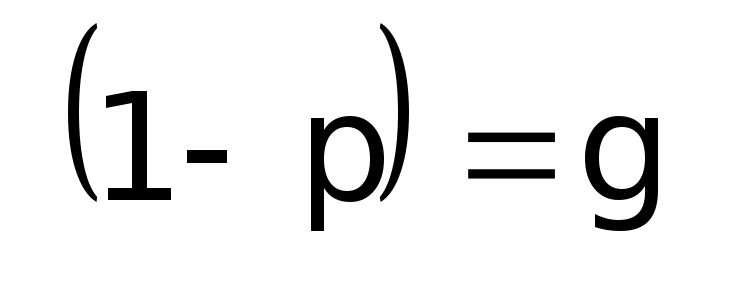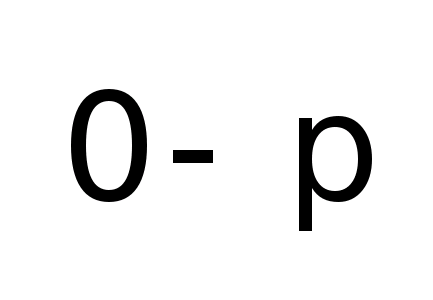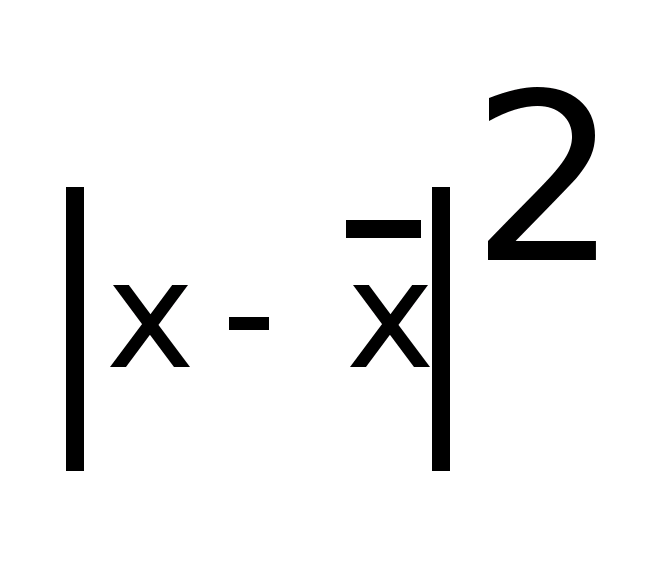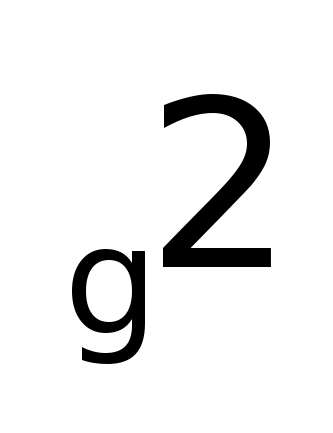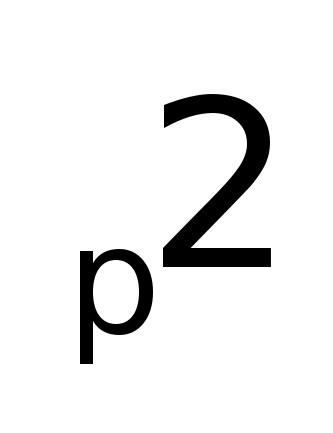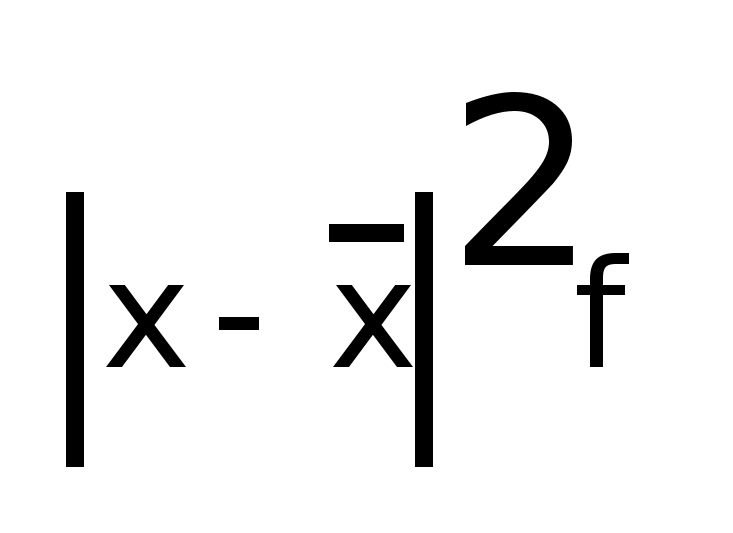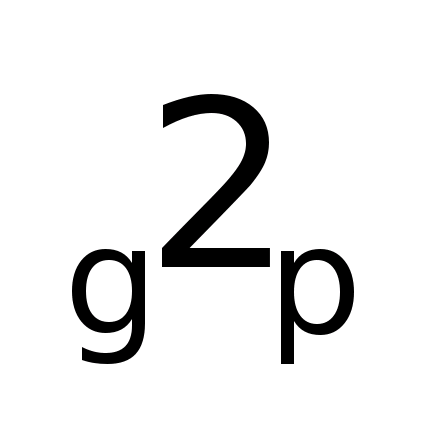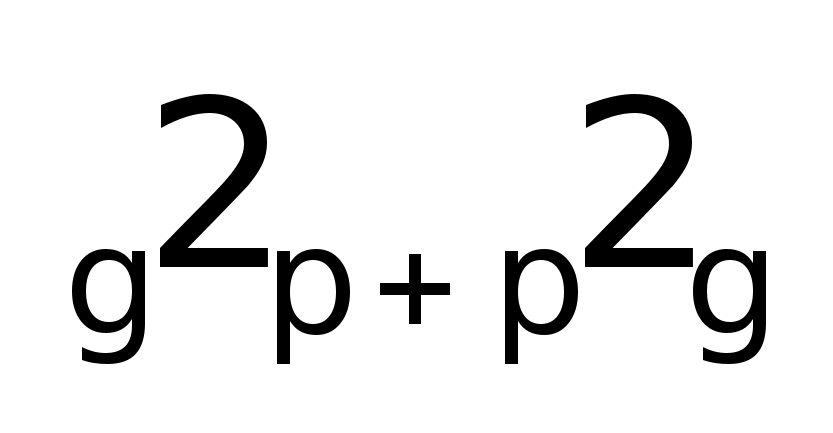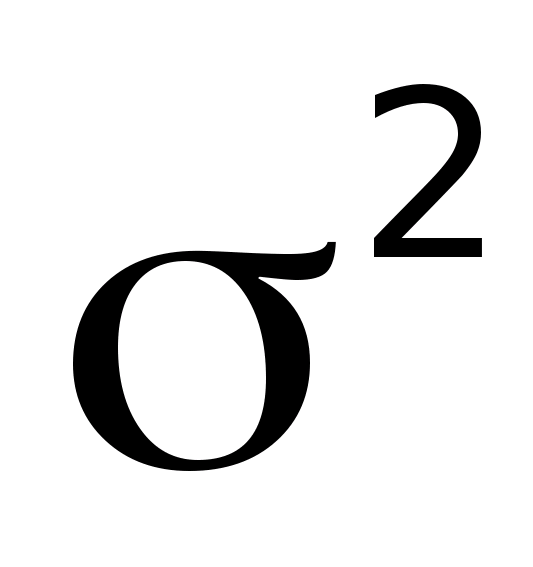Статистика (шпаргалка 2002г.)
1. Анализ рядов распределения
Ряд распределения, графики в приложении.
|
Группы |
Частота f |
S |
|
До 10 |
4 |
4 |
|
10-20 |
28 |
32 |
|
20-30 |
45 |
77 |
|
30-40 |
39 |
116 |
|
40-50 |
28 |
144 |
|
50-60 |
15 |
159 |
|
60 и выше |
10 |
169 |
|
Итого |
169 |
Мода:
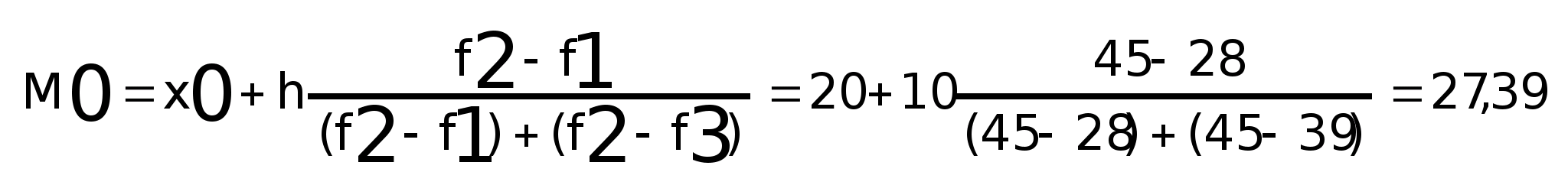
Медиана:
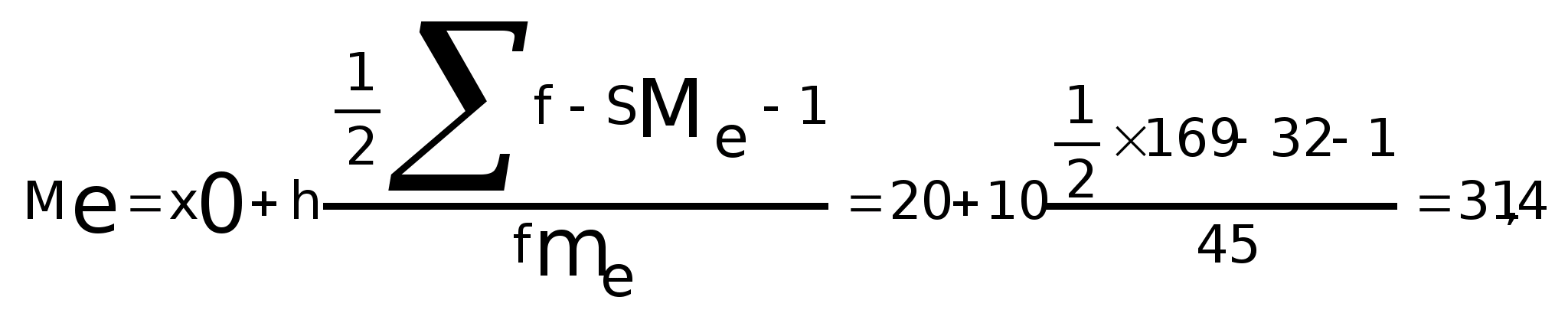
Нижний квартиль:
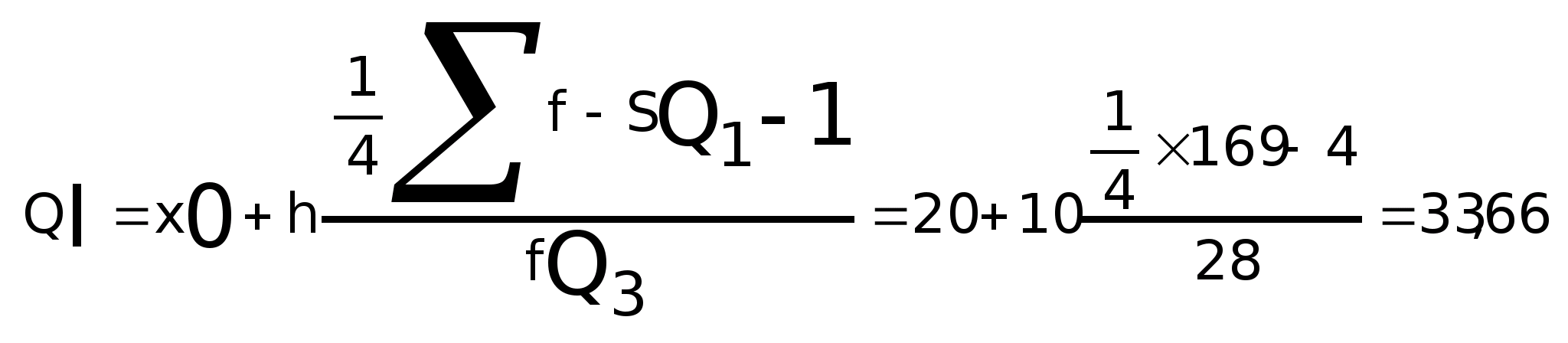
Верхний квартиль:
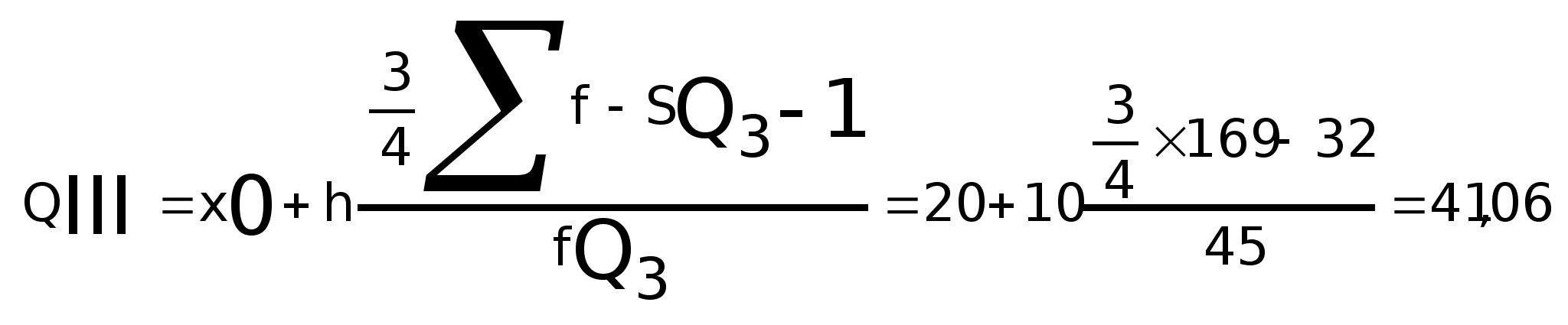
Средний уровень признака:
|
Группы |
Частота f |
x |
xf |
|
До 10 |
4 |
5 |
20 |
|
10-20 |
28 |
15 |
420 |
|
20-30 |
45 |
25 |
1125 |
|
30-40 |
39 |
35 |
1365 |
|
40-50 |
28 |
45 |
1260 |
|
50-60 |
15 |
55 |
825 |
|
60 и выше |
10 |
65 |
650 |
|
Итого |
169 |
- |
5665 |
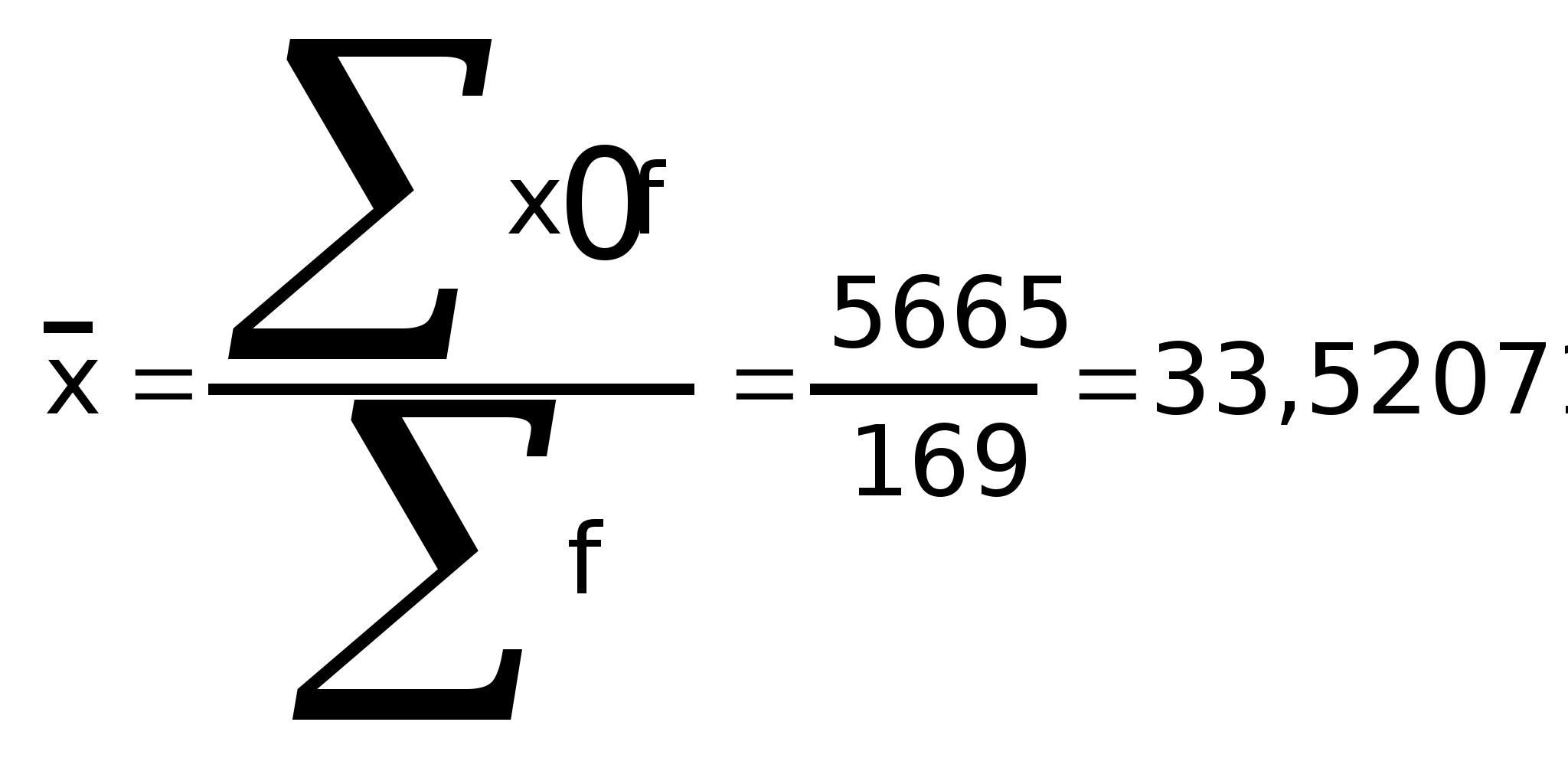
Средняя величина может рассматриваться в совокупности с другими обобщающими характеристиками, в частности, совместно с модой и медианой. Их соотношение указывает на особенность ряда распределения. В данном случае средний уровень больше моды и медианы. Асимметрия положительная, правосторонняя.
Асимметрия распределения такова:
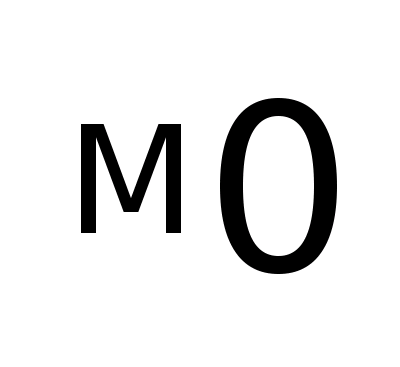 <
< 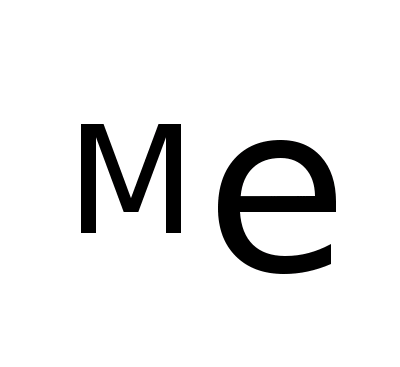 <
<
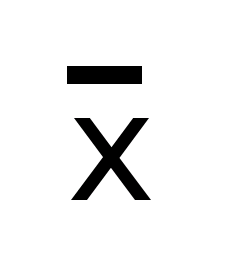 => 27,39 31,4 33,52
=> 27,39 31,4 33,52
Показатели вариации:
1) Размах вариации R
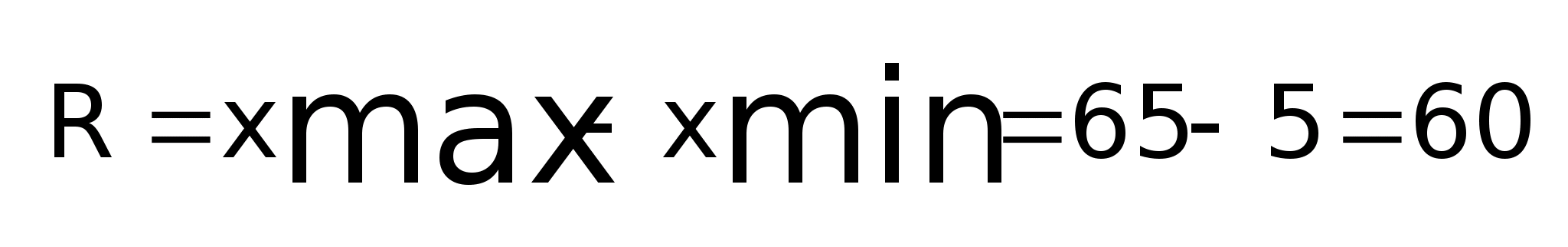
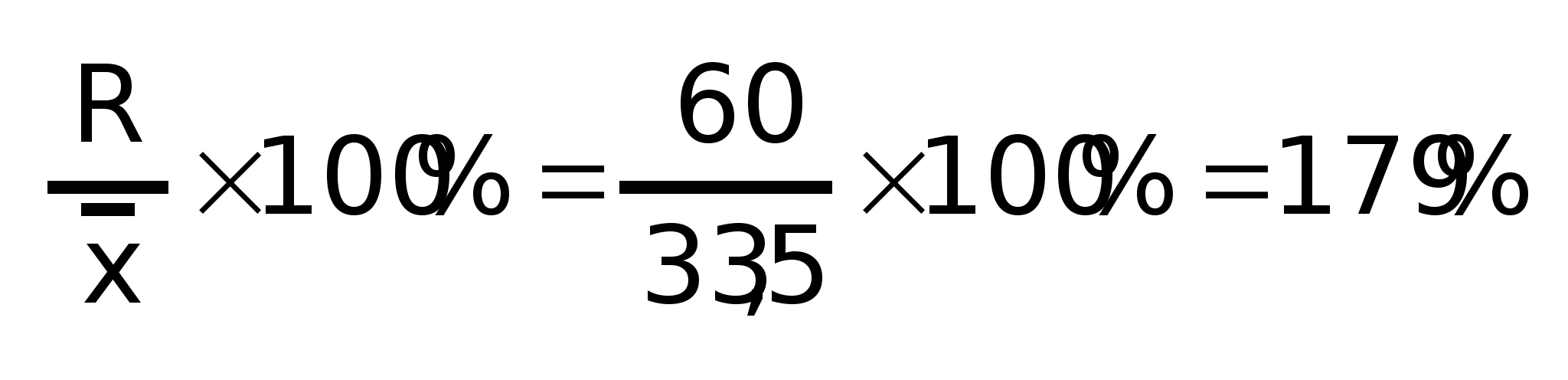
2) Среднее
линейное отклонение
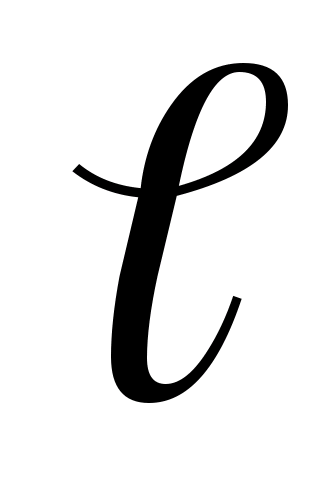
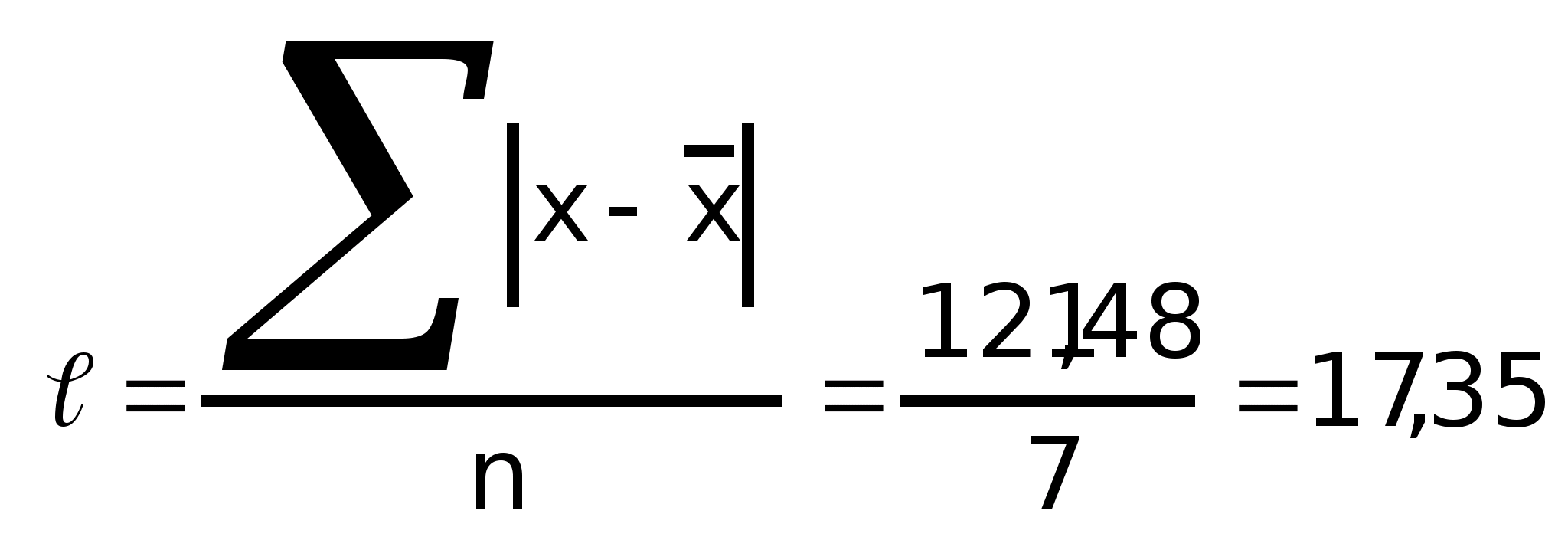 (простая)
(простая)
|
Группы |
f |
x |
xf |
S |
|
|
(x- |
f(x- |
x2 |
x2f |
|
До 10 |
4 |
5 |
20 |
4 |
114,08 |
28,52 |
813,43 |
3253,72 |
25 |
100 |
|
10-20 |
28 |
15 |
420 |
32 |
518,58 |
18,52 |
343,02 |
9604,47 |
225 |
6300 |
|
20-30 |
45 |
25 |
1125 |
77 |
383,43 |
8,52 |
72,60 |
3267,11 |
625 |
28125 |
|
30-40 |
39 |
35 |
1365 |
116 |
57,69 |
1,48 |
2,19 |
85,34 |
1225 |
47775 |
|
40-50 |
28 |
45 |
1260 |
144 |
321,42 |
11,48 |
131,77 |
3689,67 |
2025 |
56700 |
|
50-60 |
15 |
55 |
825 |
159 |
322,19 |
21,48 |
461,36 |
6920,39 |
3025 |
45375 |
|
60 и в. |
10 |
65 |
650 |
169 |
314,79 |
31,48 |
990,95 |
9909,46 |
4225 |
42250 |
|
Итого |
169 |
- |
5665 |
- |
2032,18 |
121,48 |
- |
36730,18 |
226625 |
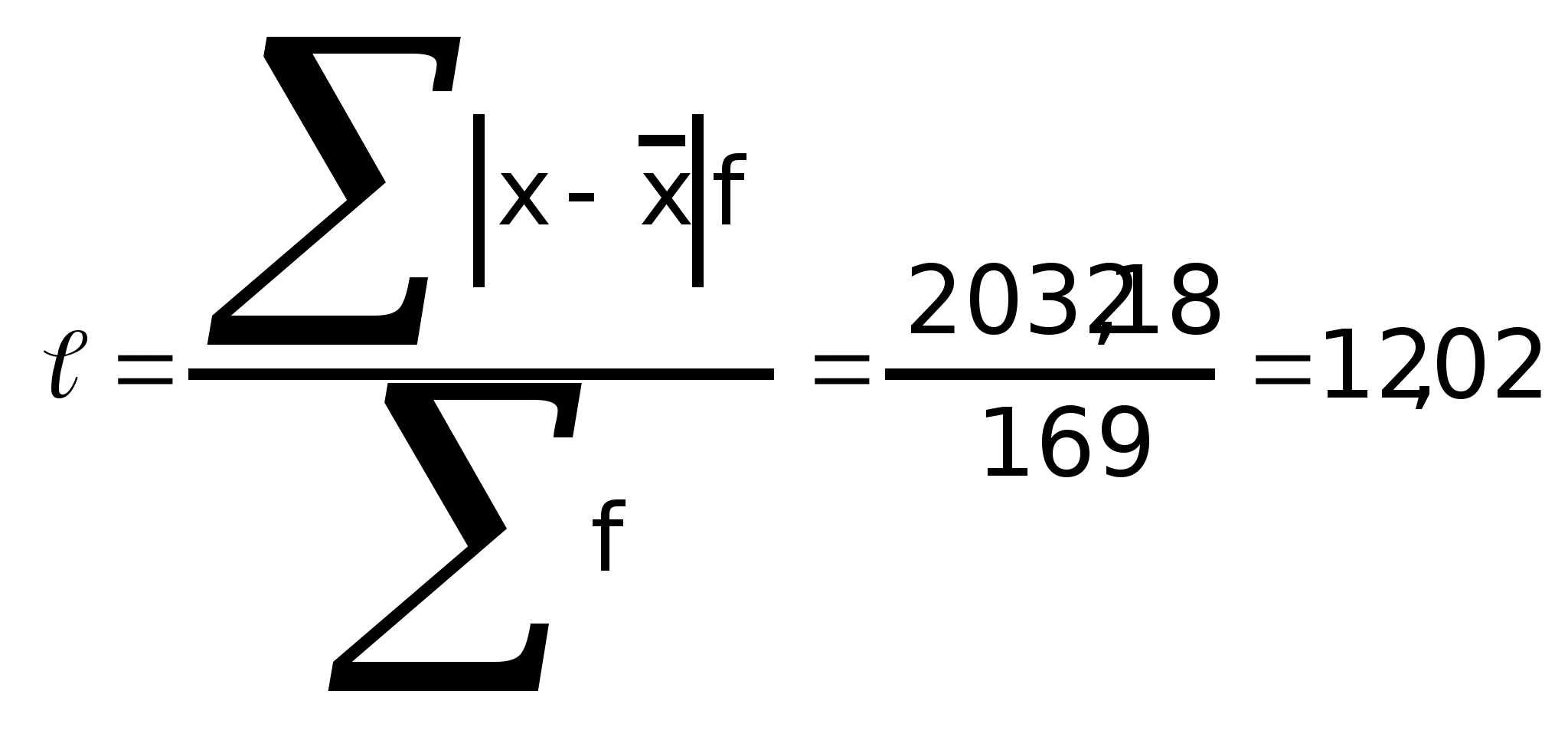 (взвешенная)
(взвешенная)
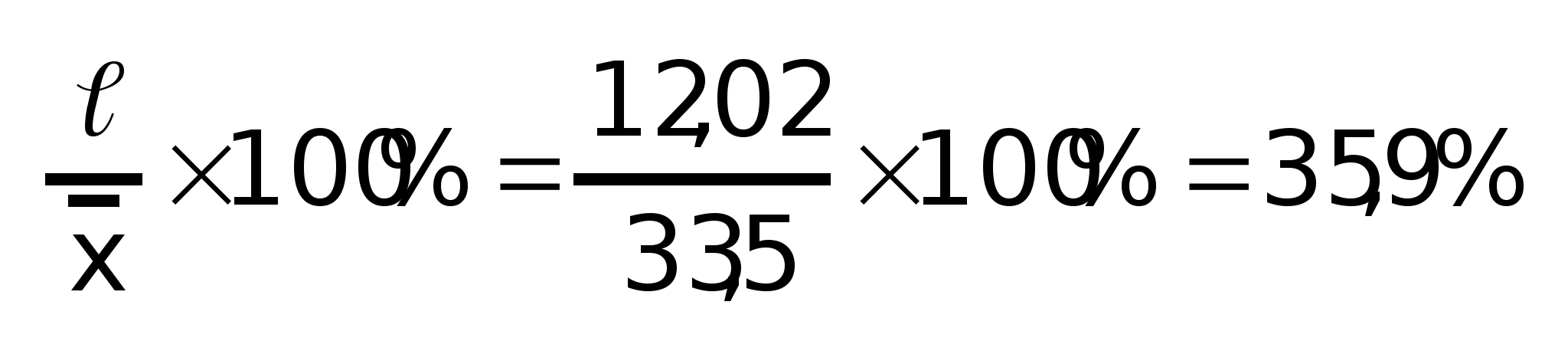
3) Дисперсия
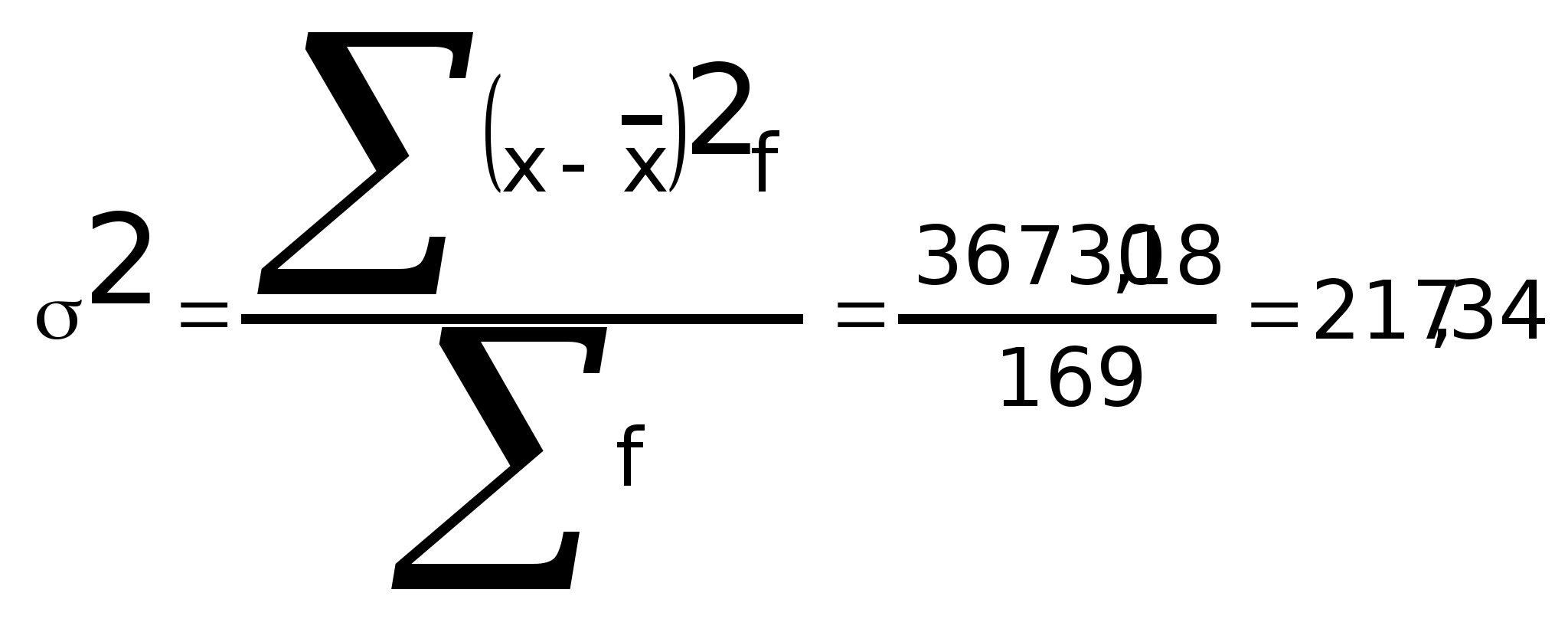
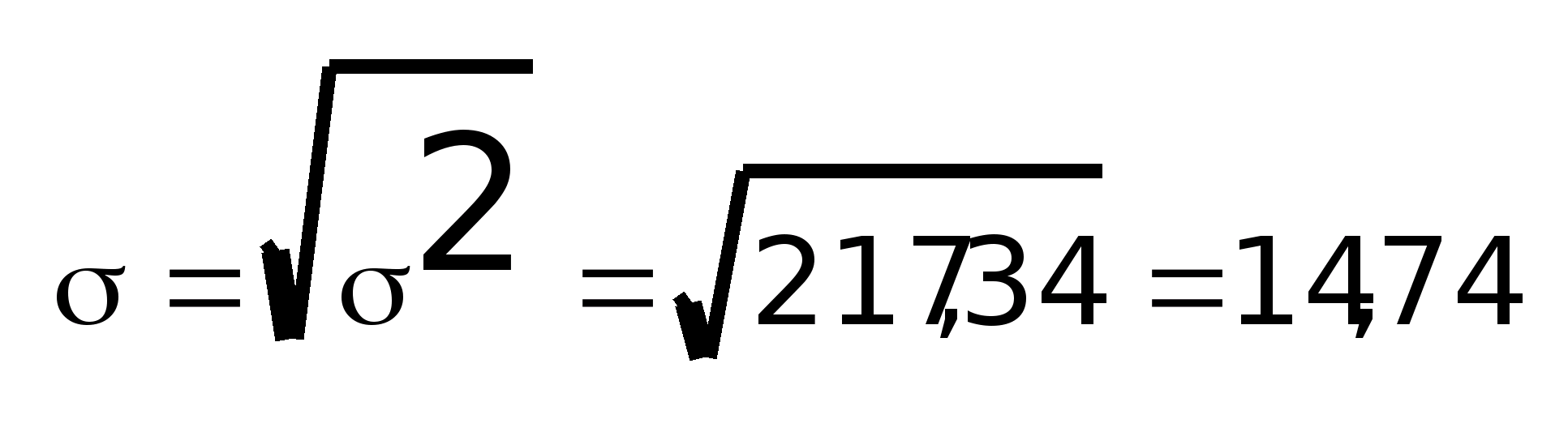
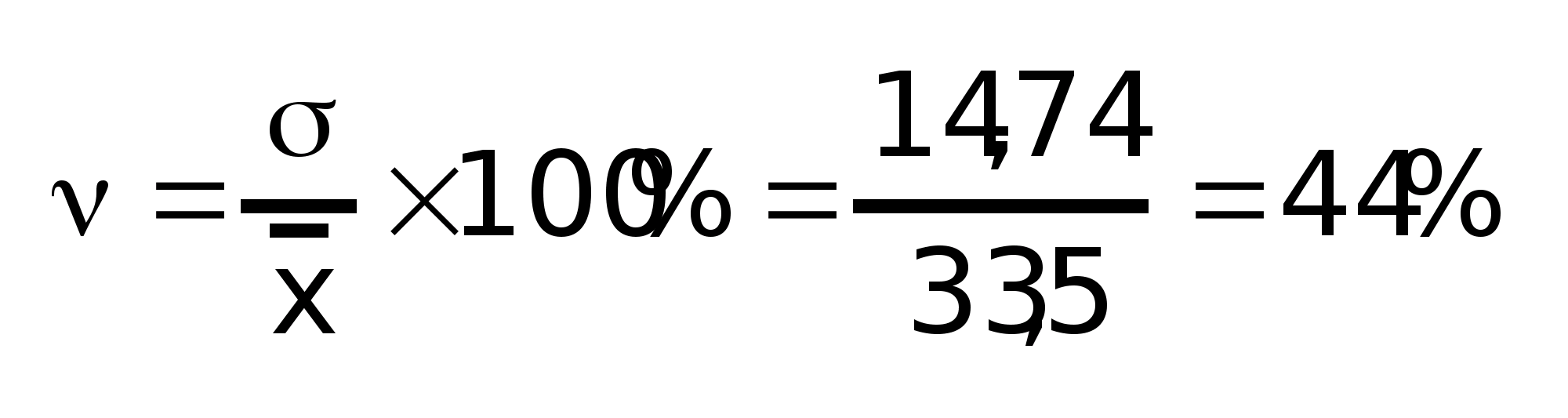
Другие методы расчета дисперсии:
1. Первый метод
|
Группы |
f |
x |
|
|
|
|
|
До 10 |
4 |
5 |
-3 |
9 |
-12 |
36 |
|
10-20 |
28 |
15 |
-2 |
4 |
-56 |
112 |
|
20-30 |
45 |
25 |
-1 |
1 |
-45 |
45 |
|
30-40 |
39 |
35 |
0 |
0 |
0 |
0 |
|
40-50 |
28 |
45 |
1 |
1 |
28 |
28 |
|
50-60 |
15 |
55 |
2 |
4 |
30 |
60 |
|
60 и выше |
10 |
65 |
3 |
9 |
30 |
90 |
|
Итого |
169 |
- |
- |
- |
-25 |
371 |
Условное начало С = 35
Величина интервала d = 10
Первый условный момент:
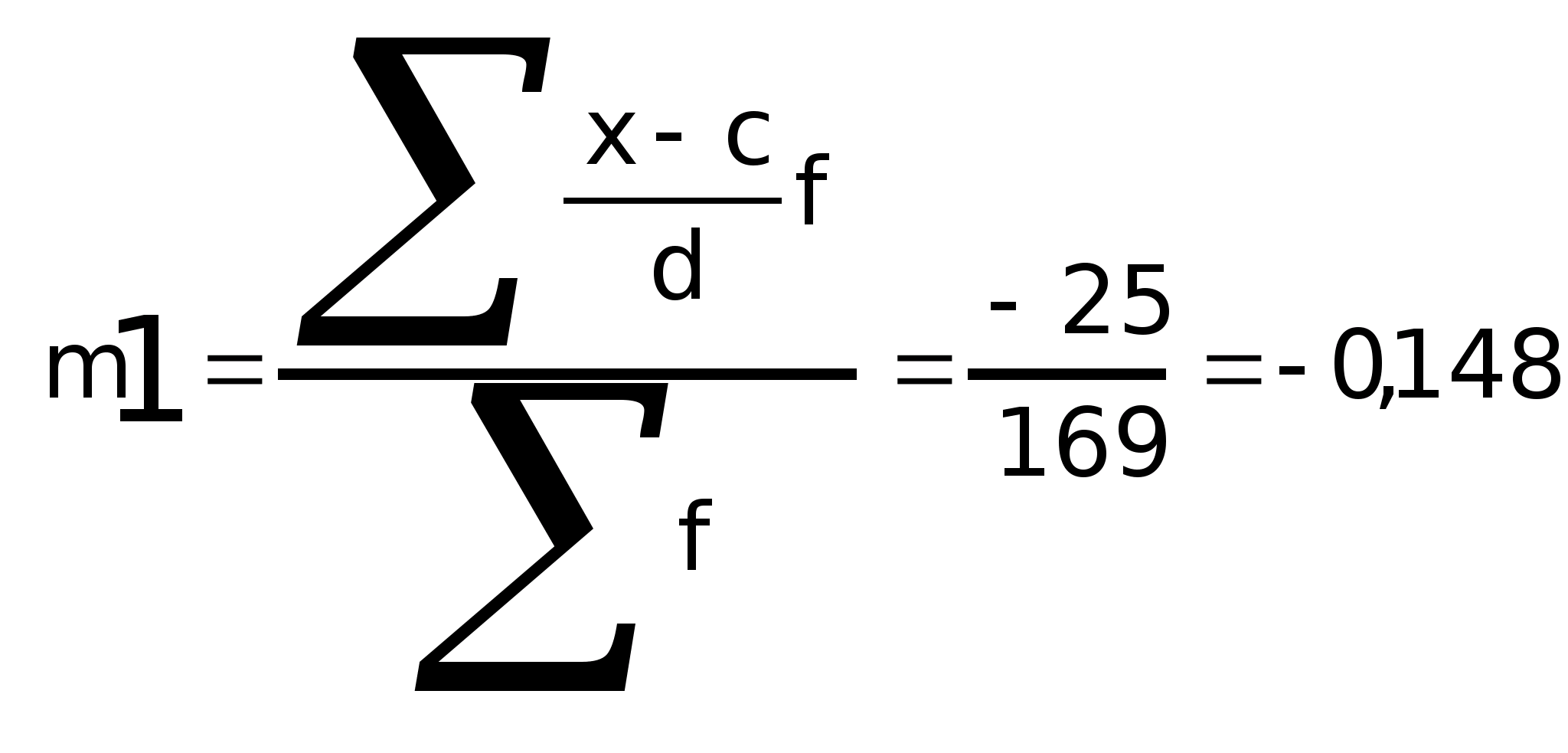
Средний уровень признака:
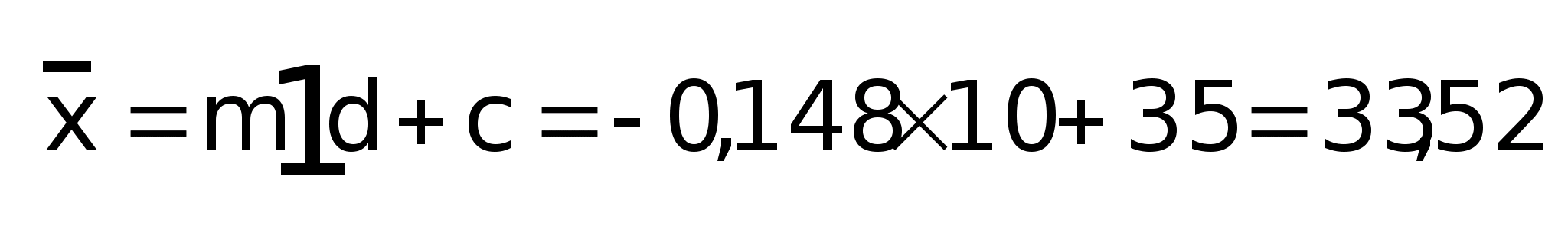
Второй условный момент:
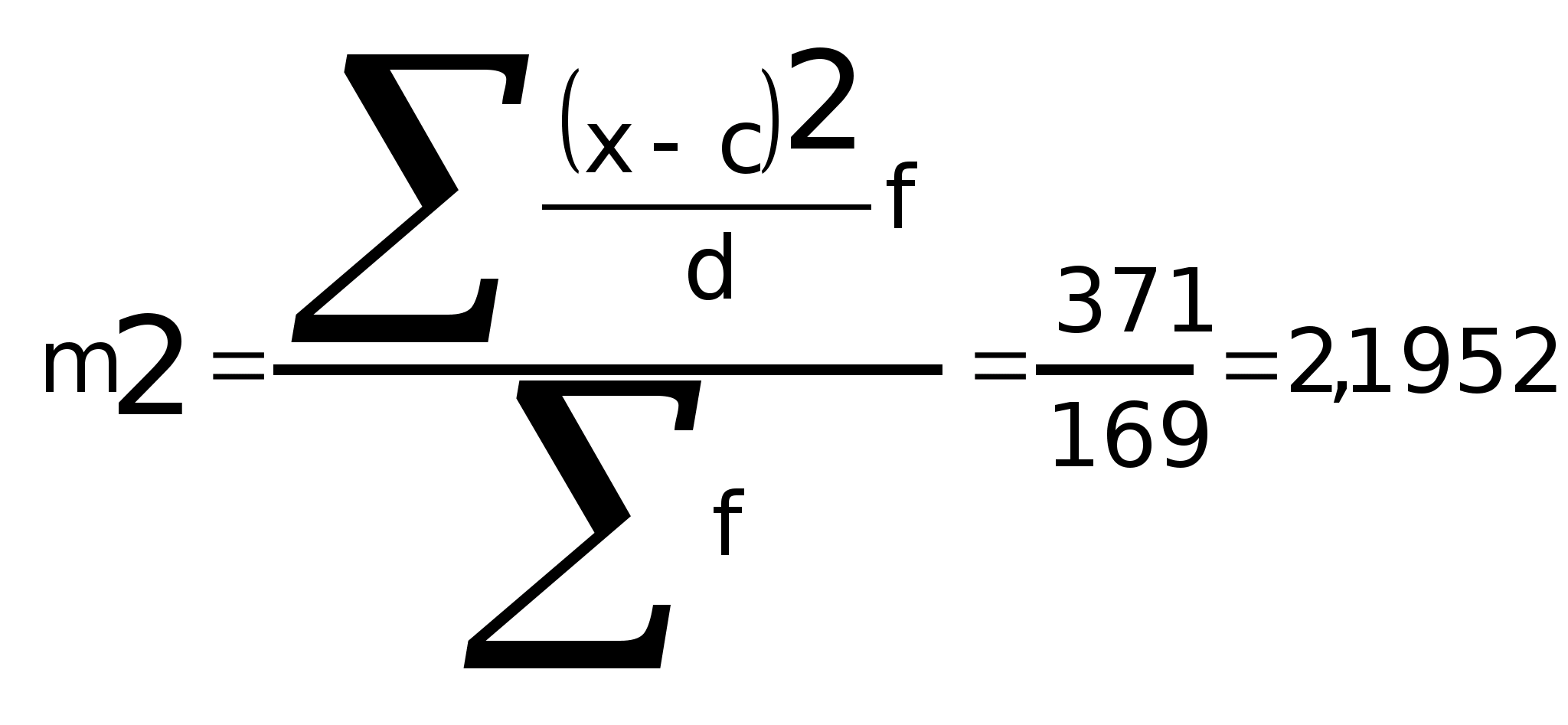
Дисперсия признака:
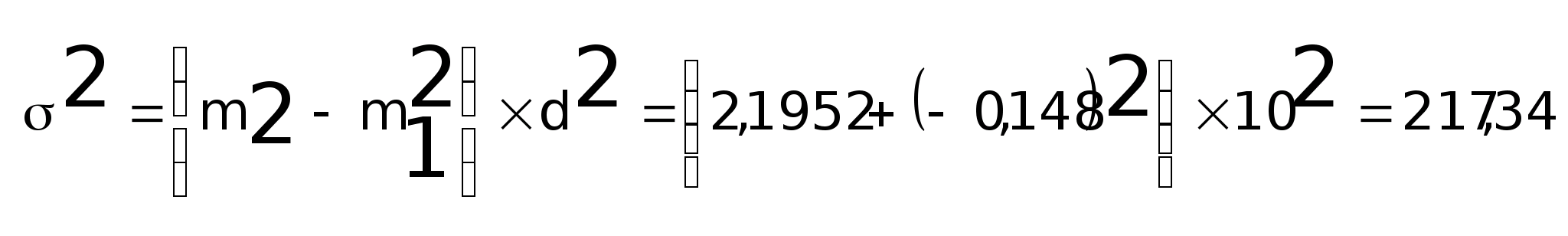
2. Второй метод
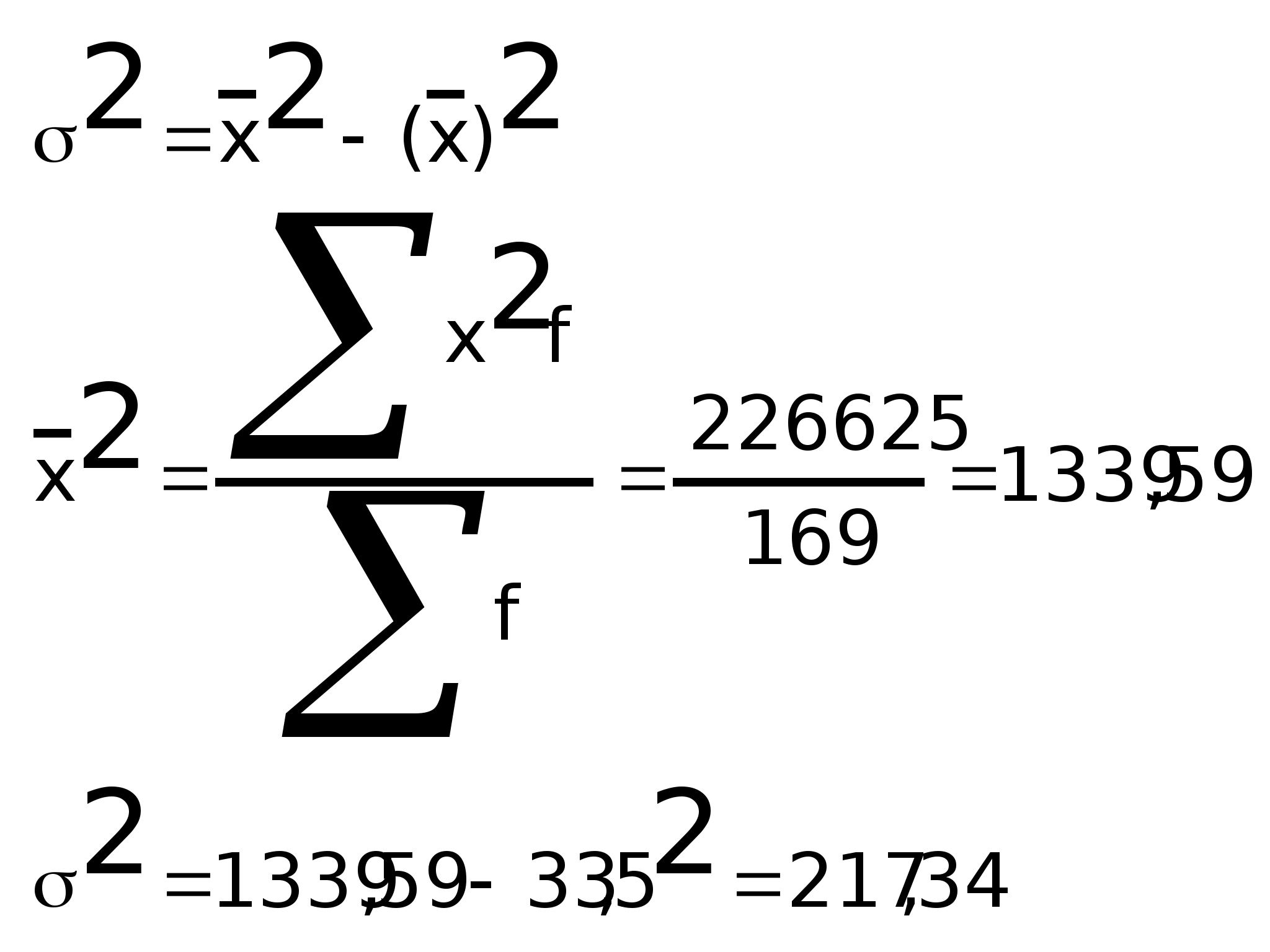
Методика расчета дисперсии альтернативного признака:
Альтернативным называется признак, который принимает значение «да» или «нет». Этот признак выражает как количественный «да»-1, «нет»-0, это значение x , тогда для него надо определить среднюю и дисперсию.
Вывод формулы:
|
Признак х |
1 |
0 |
всего |
|
Ч |
p |
g |
p + g = 1 |
|
xf |
1p |
0g |
p + 0 = p |
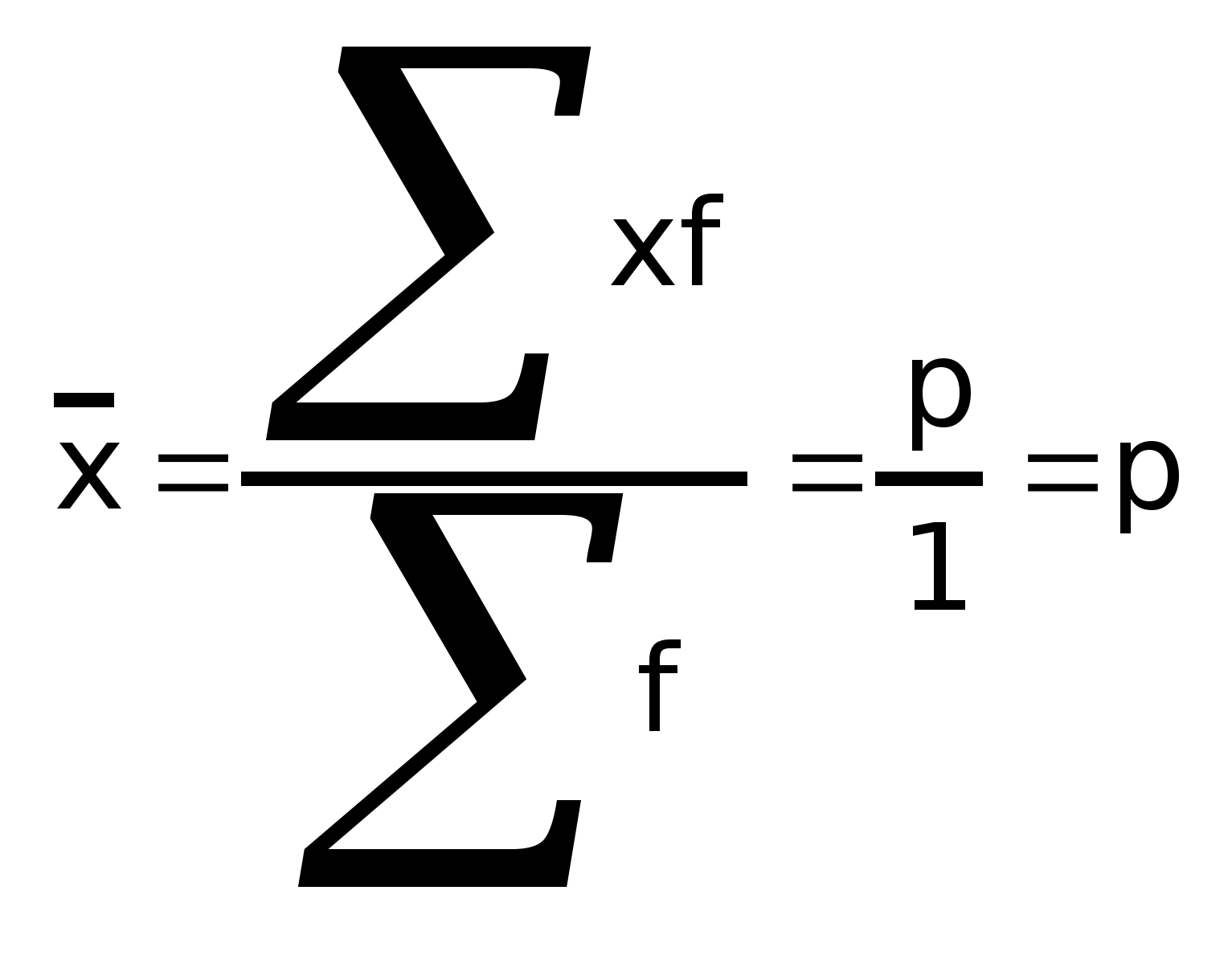
Средняя альтернативного признака равна доле единиц, которые этим признаком обладают.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
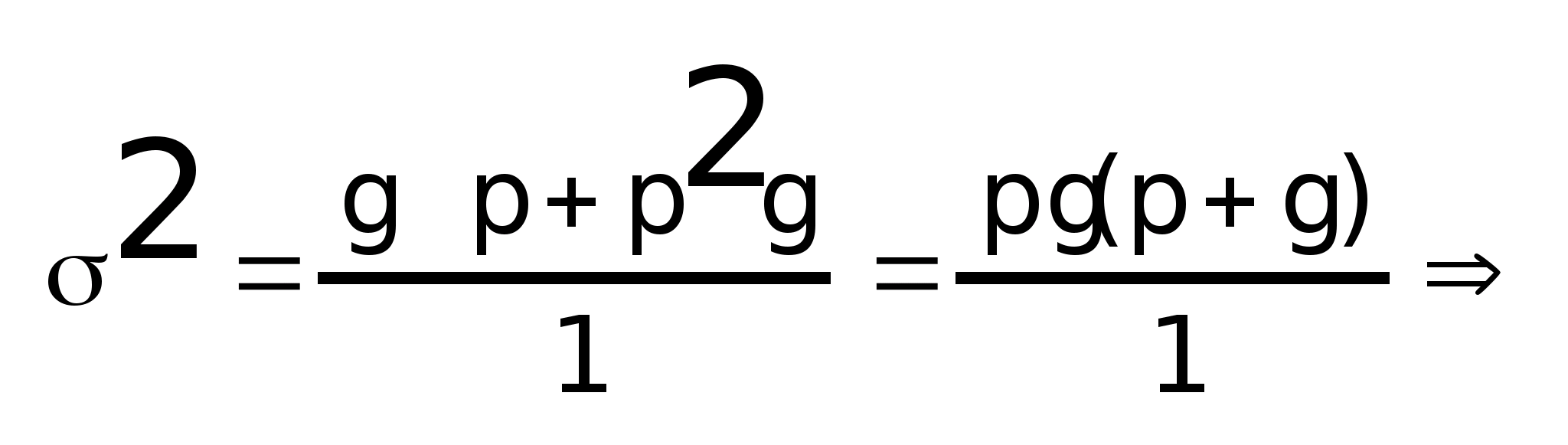
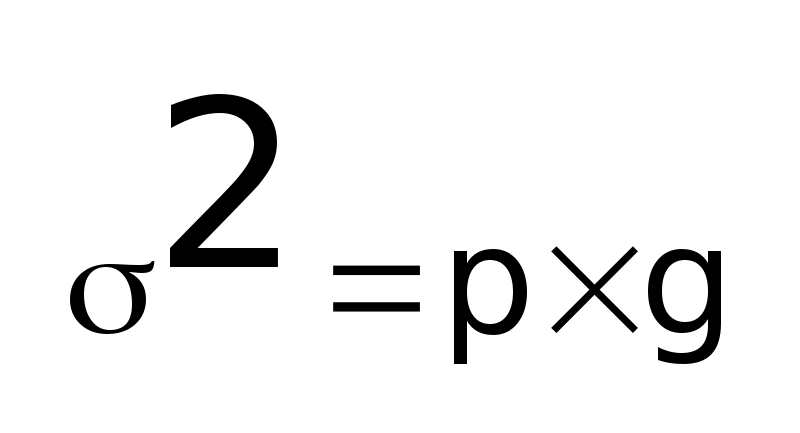 - Дисперсия альтернативного признака.
Она равна произведению доли единиц,
обладающих признаком на ее дополнение
до 1.
- Дисперсия альтернативного признака.
Она равна произведению доли единиц,
обладающих признаком на ее дополнение
до 1.
Дисперсия альтернативного признака используется при расчете ошибки для доли.
|
p |
g |
|
|
0,1 |
0,9 |
0,09 |
|
0,2 |
0,8 |
0,16 |
|
0,3 |
0,7 |
0,21 |
|
0,4 |
0,6 |
0,24 |
|
0,5 |
0,5 |
max 0,25 |
|
0,6 |
0,4 |
0,24 |
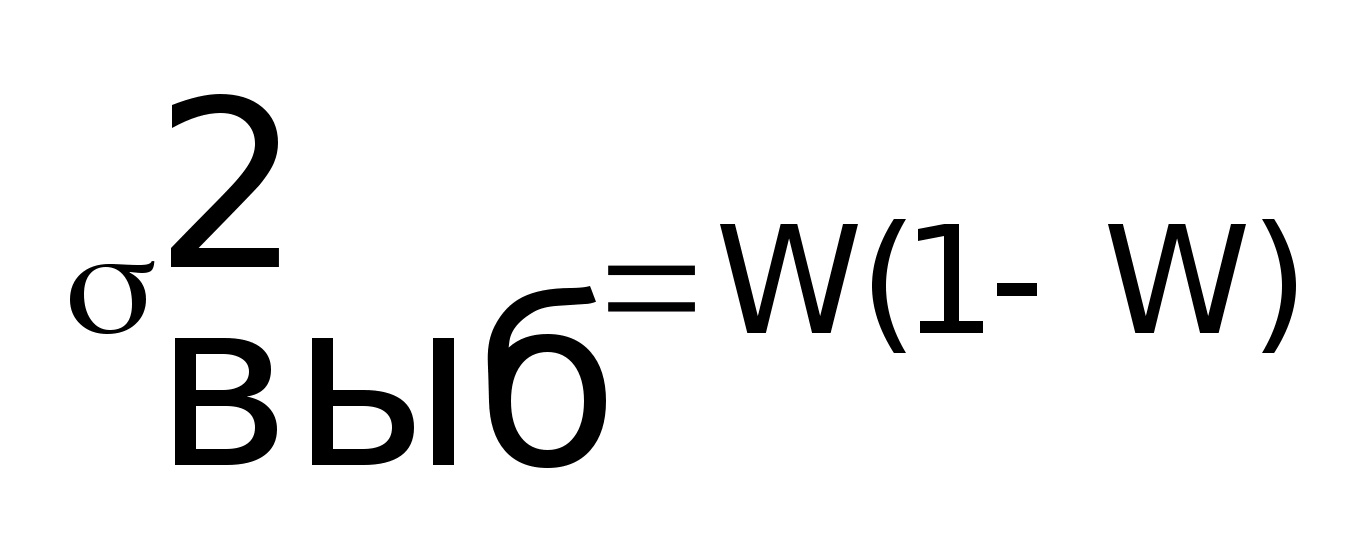 ,
W
– выборочная доля.
,
W
– выборочная доля.
Виды дисперсии и правило их сложения:
Виды:
1. Межгрупповая дисперсия.
2. Общая дисперсия.
3. Средняя дисперсия.
4. Внутригрупповая дисперсия.
У всей совокупности может быть рассчитана общая средняя и общая дисперсия.
1.
 общая и
общая и
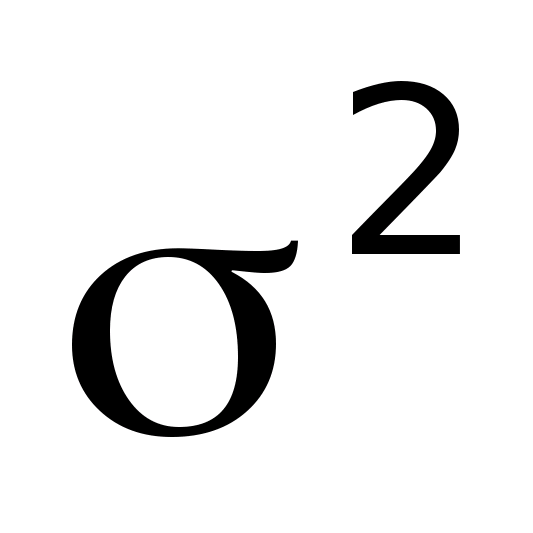 общая.
общая.
2. По каждой
группе определяется своя средняя
величина и своя дисперсия:
 a,
a,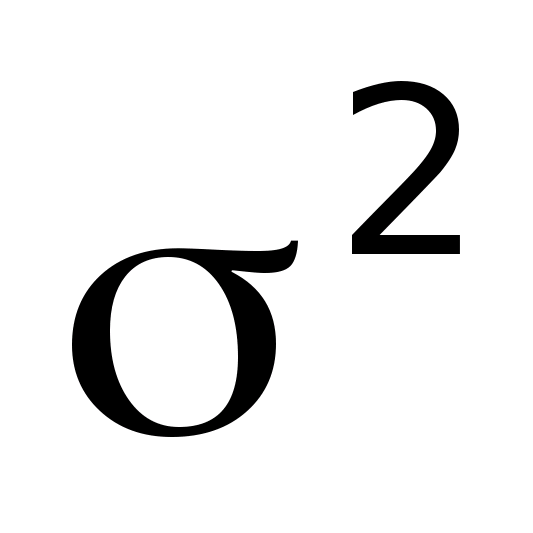 a;
a;
 б,
б,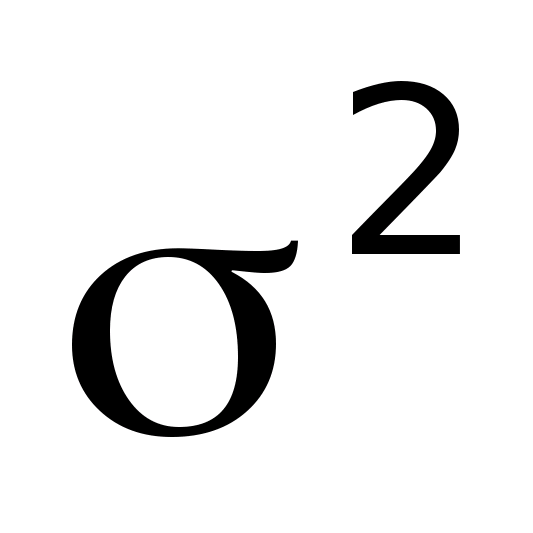 б;
б;
 i,
i,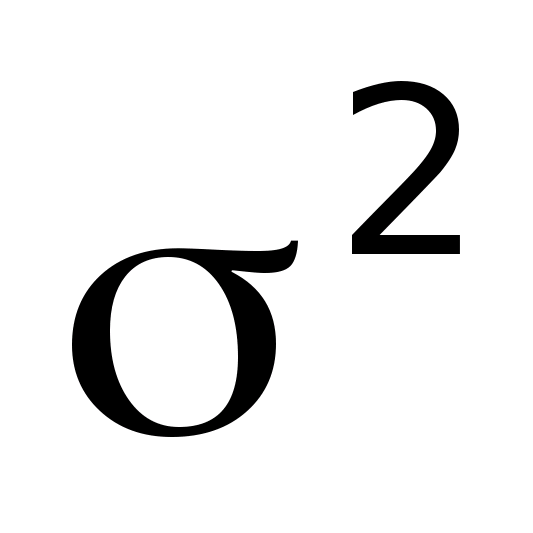 i
i
3. Групповые
средние
 i
не одинаковые. Чем больше различия
между группами, тем больше различаются
групповые средние и отличаются от общей
средней.
i
не одинаковые. Чем больше различия
между группами, тем больше различаются
групповые средние и отличаются от общей
средней.
Это позволяет рассчитать дисперсию, которая показывает отклонение групповых средних от общей средней:
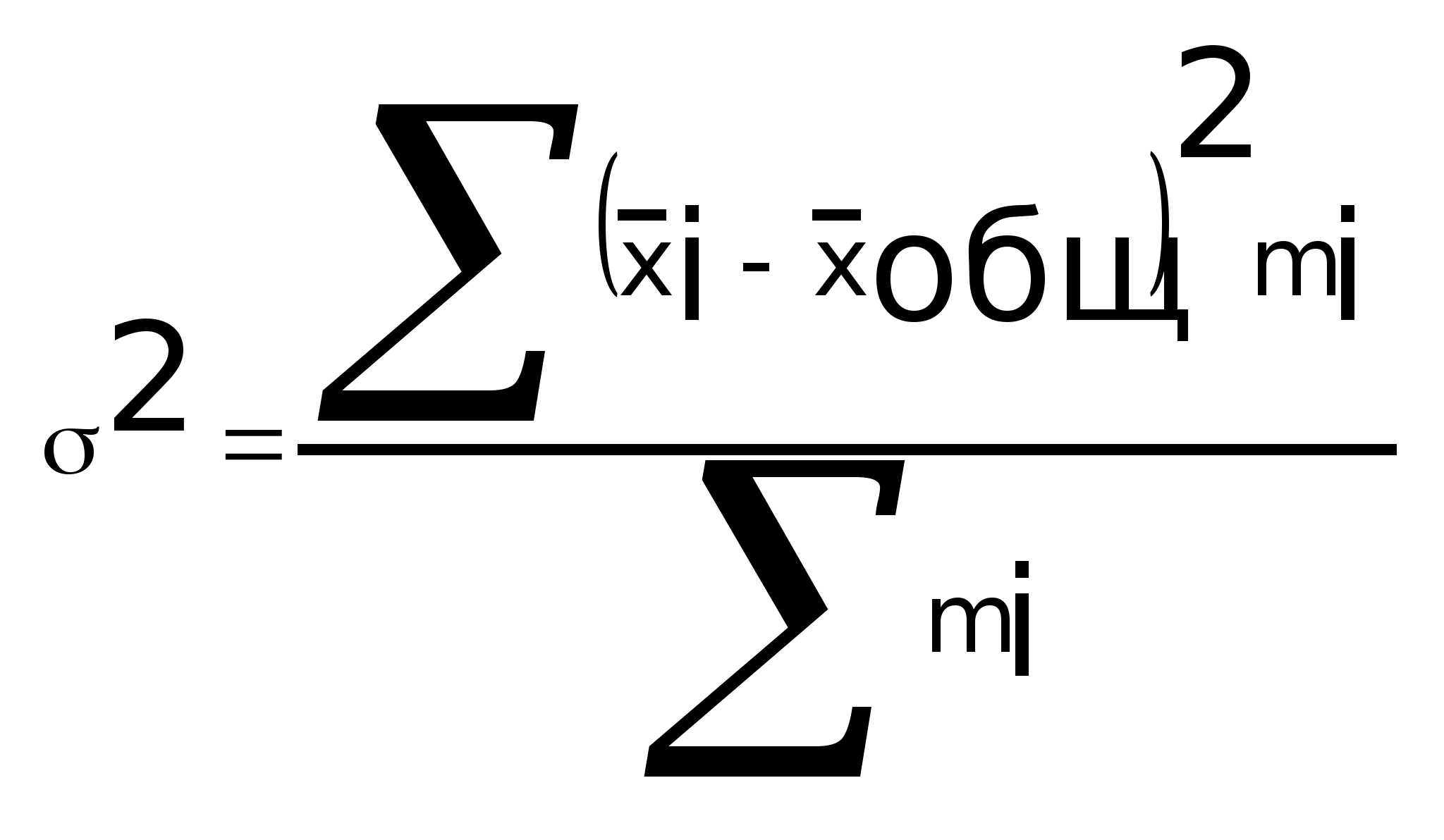 - межгрупповая
дисперсия, где m>i>
– численность единиц в каждой группе.
- межгрупповая
дисперсия, где m>i>
– численность единиц в каждой группе.
В каждой
группе имеется своя колеблемость –
внутригрупповая
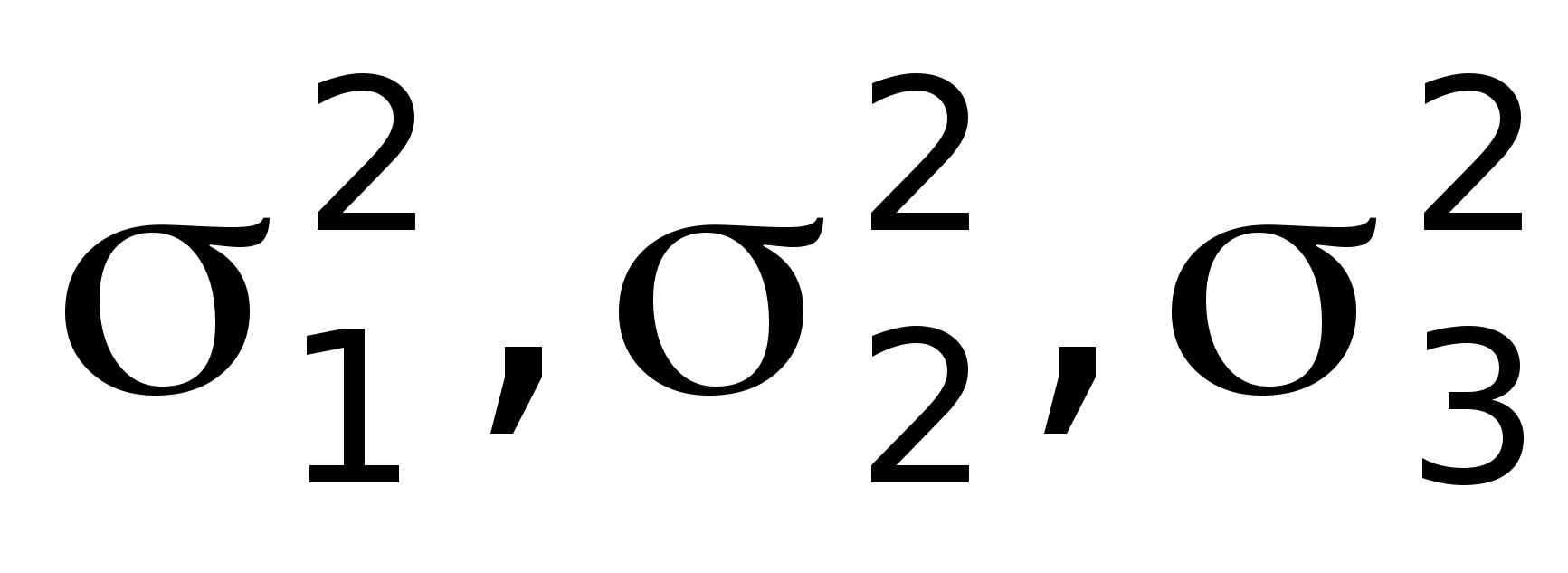 .
Она не одинакова, поэтому определяется
средняя из внутригрупповых дисперсий:
.
Она не одинакова, поэтому определяется
средняя из внутригрупповых дисперсий:
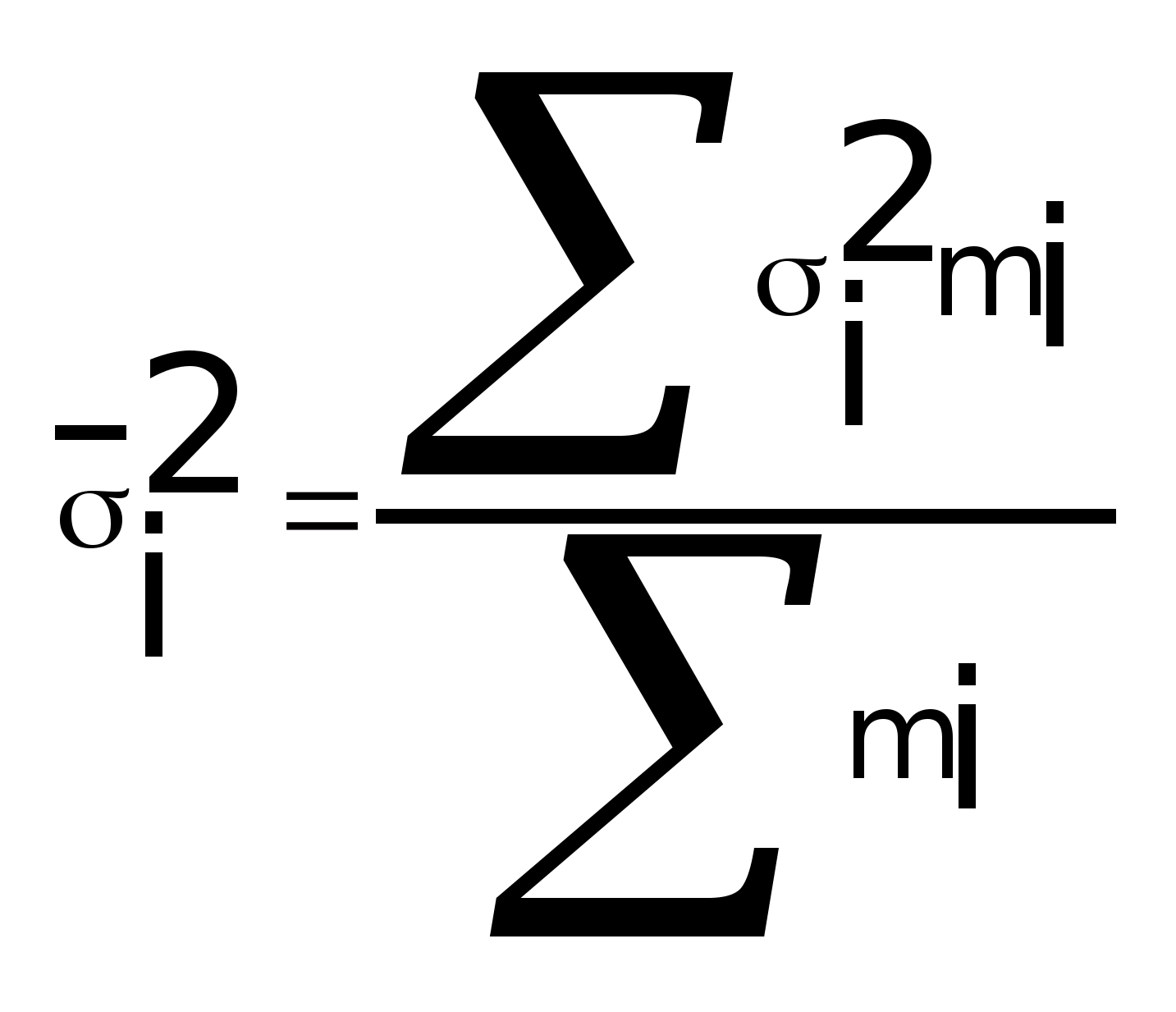
Эти дисперсии находятся в определенном соотношении. Общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:
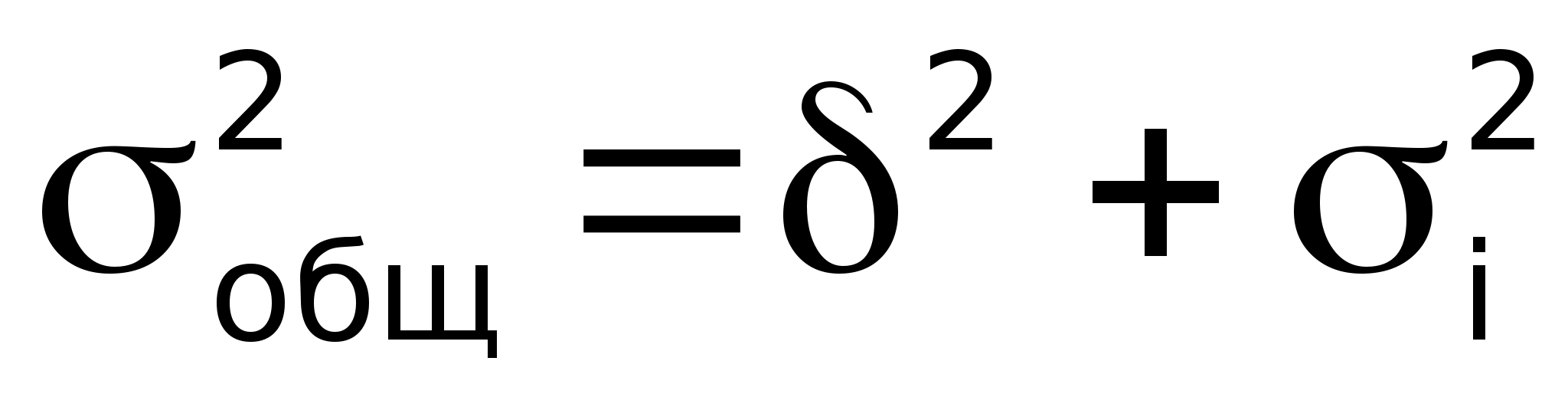 - правило сложения
дисперсий.
- правило сложения
дисперсий.
Соотношения дисперсий используются для оценки тесноты связей между факторами влияния изучаемого фактора – это межгрупповая дисперсия. Все остальные факторы – остаточные факторы.
2. Ряды динамики
Ряд динамики, график ряда динамики в приложении.
|
Год |
Уровень |
|
1 |
40,6 |
|
2 |
41,5 |
|
3 |
49,5 |
|
4 |
43,6 |
|
5 |
39,2 |
|
6 |
40,7 |
|
7 |
38,2 |
|
8 |
36,5 |
|
9 |
38,0 |
|
10 |
38,7 |
|
11 |
39,4 |
Средняя хронологическая:
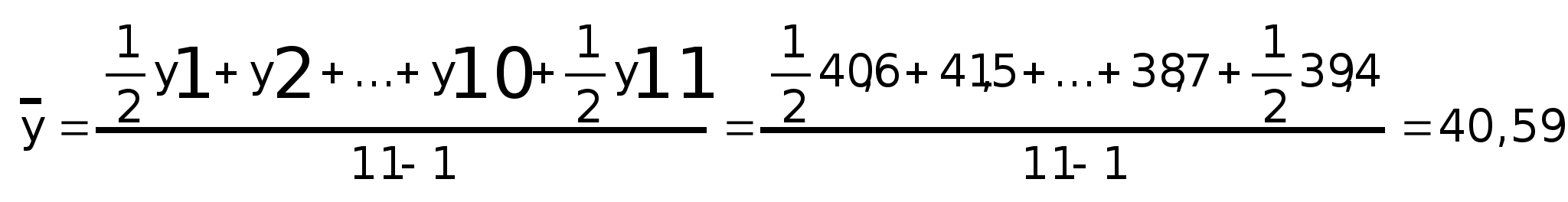
Производные показатели ряда динамики:
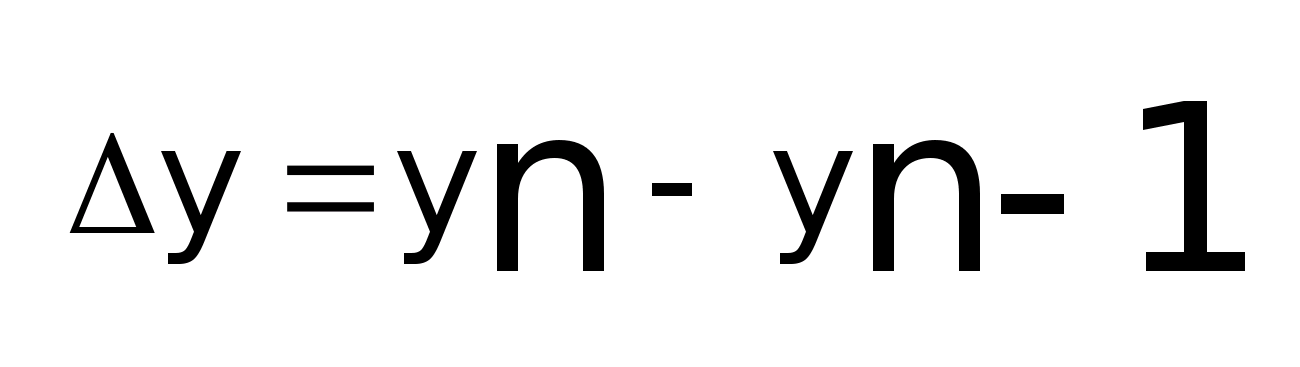
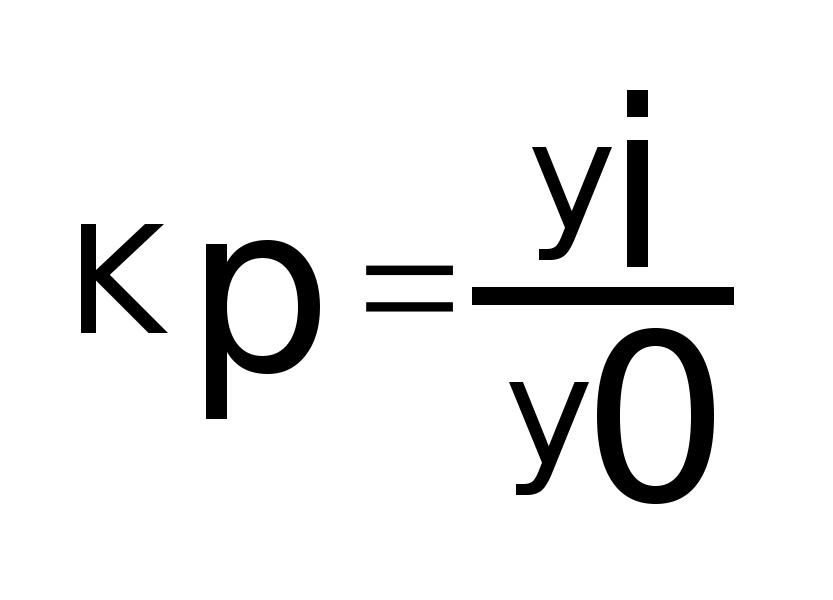 - коэффициент роста,
базисный
- коэффициент роста,
базисный
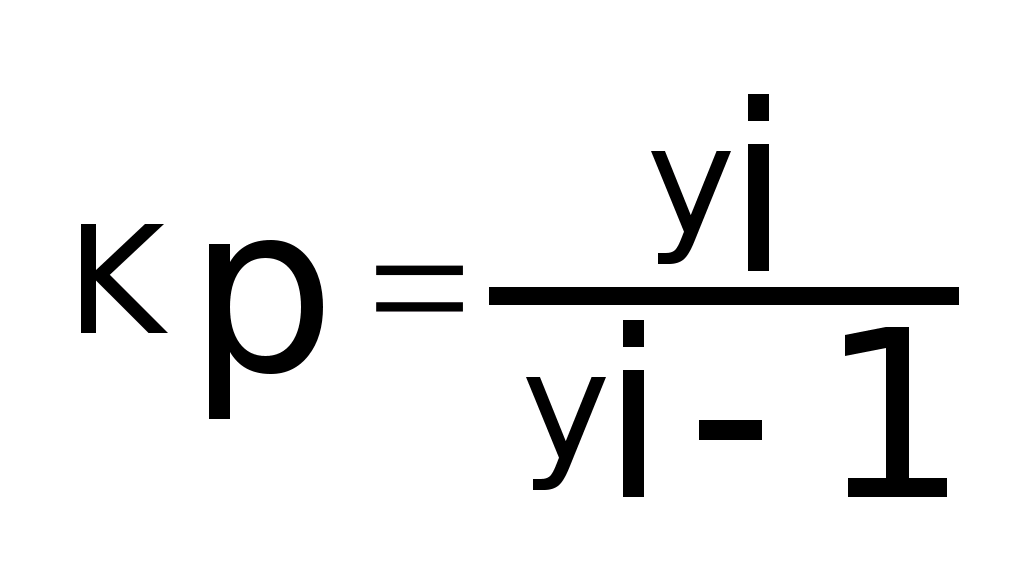 - коэффициент роста,
цепной
- коэффициент роста,
цепной
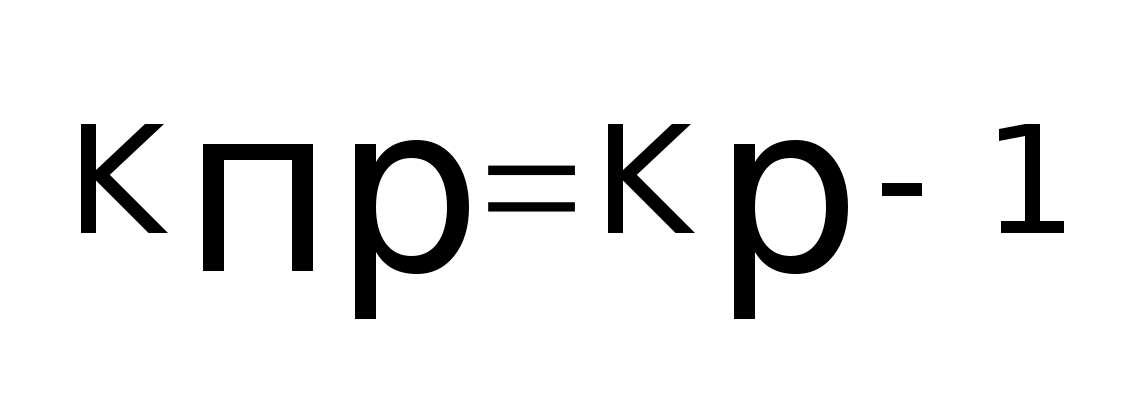 - коэффициент прироста
- коэффициент прироста
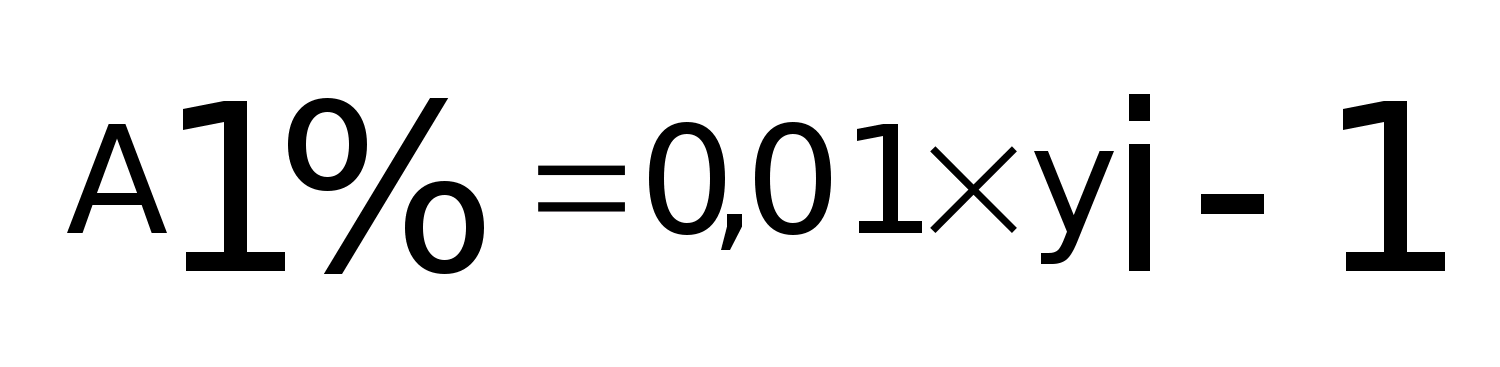 - абсолютное значение
одного процента прироста
- абсолютное значение
одного процента прироста
-
Год
Уровень
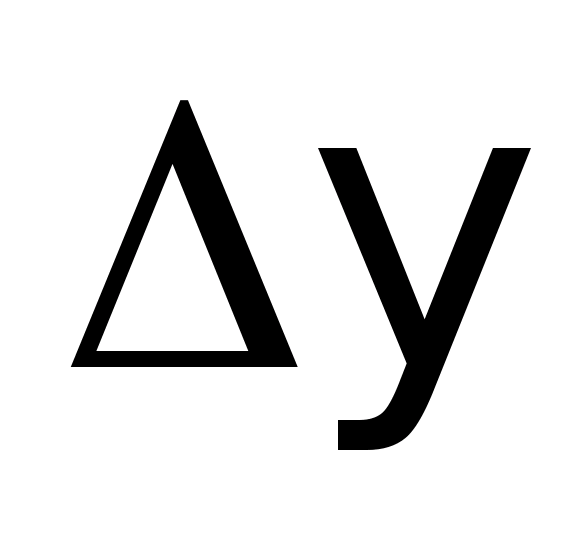
Темпы роста %
Темпы прироста %
А>1%>
Базисные
Цепные
Базисные
Цепные
1
40,6
-
100
-
-
-
-
2
41,5
0,9
102,2167
102,2167
2,216749
2,216749
0,406
3
49,5
8
121,9212
119,2771
21,92118
19,27711
0,415
4
43,6
-5,9
107,3892
88,08081
7,389163
-11,9192
0,495
5
39,2
-4,4
96,55172
89,90826
-3,44828
-10,0917
0,436
6
40,7
1,5
100,2463
103,8265
0,246305
3,826531
0,392
7
38,2
-2,5
94,08867
93,85749
-5,91133
-6,14251
0,407
8
36,5
-1,7
89,90148
95,54974
-10,0985
-4,45026
0,382
9
38
1,5
93,59606
104,1096
-6,40394
4,109589
0,365
10
38,7
0,7
95,3202
101,8421
-4,6798
1,842105
0,38
11
39,4
0,7
97,04433
101,8088
-2,95567
1,808786
0,387
Взаимосвязь цепных и базисных коэффициентов роста:
Произведение последовательных цепных коэффициентов равно базисному:
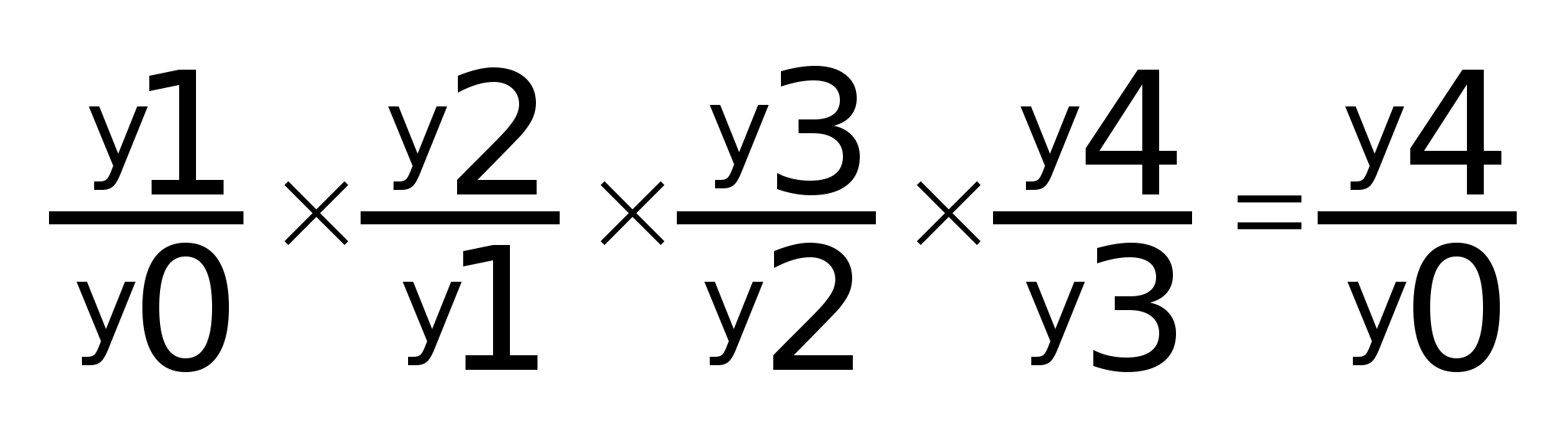
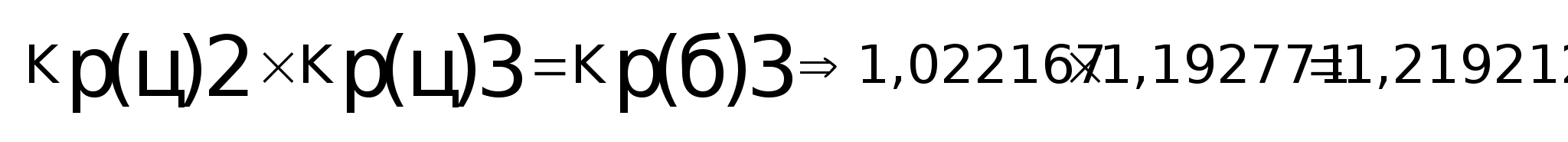 и т. д.
и т. д.
Частное от деления одного базисного равно цепному коэффициенту:
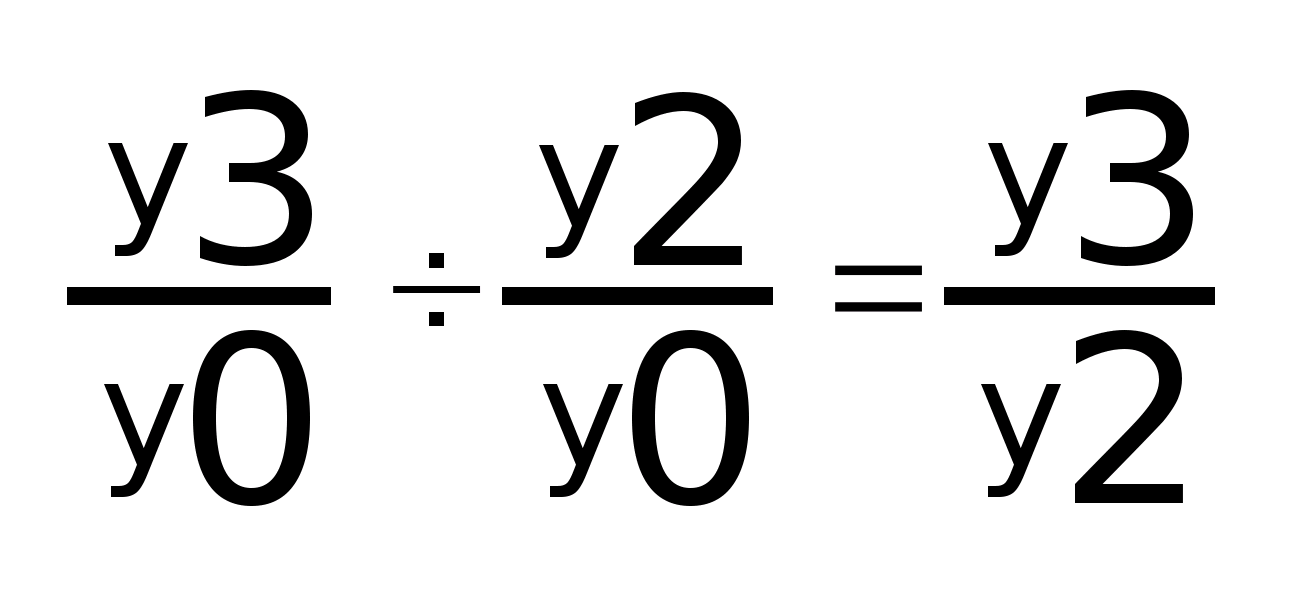
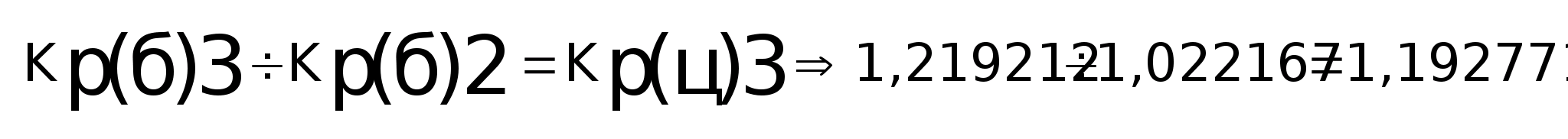 и т. д.
и т. д.
Средний абсолютный прирост:
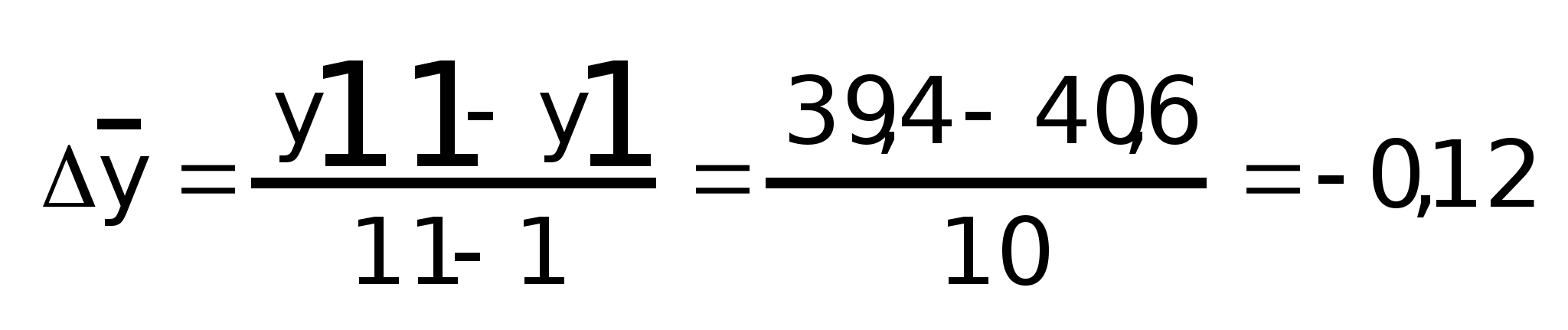
Средний годовой коэффициент роста:
1)
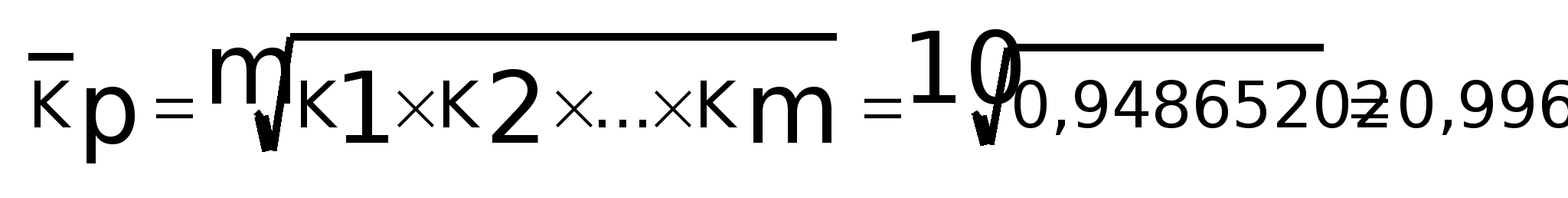
2)
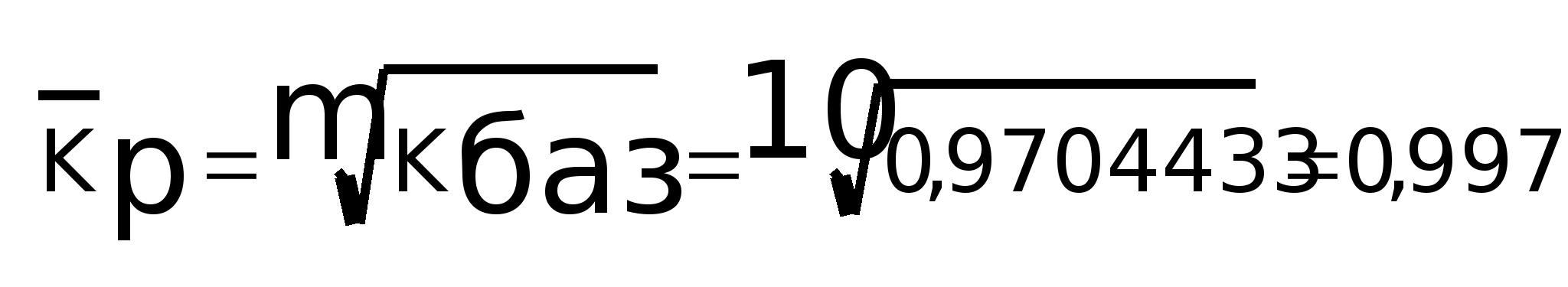
3)
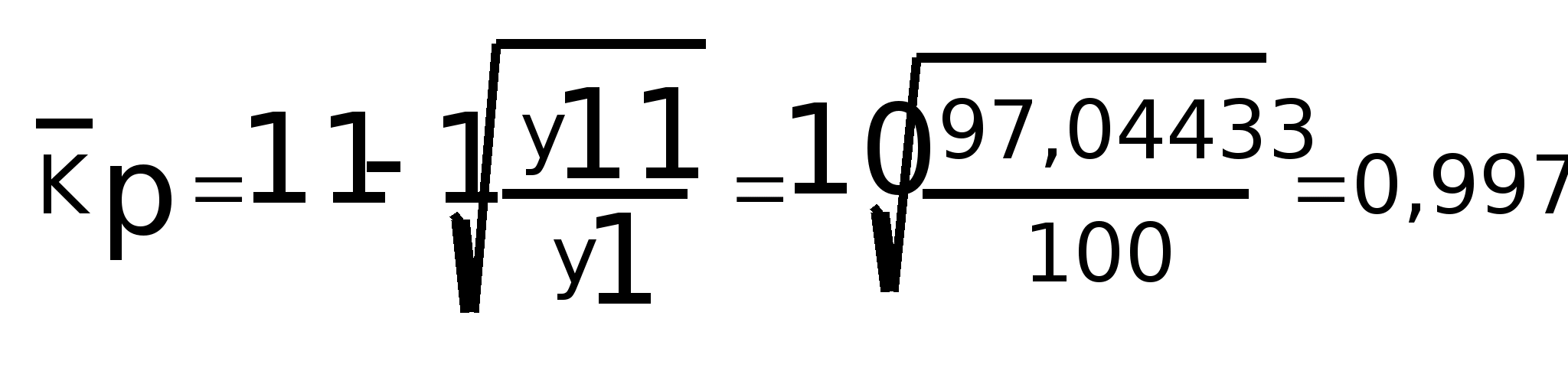
Анализ тенденции изменений условий ряда:
Анализ состоит в том, чтобы выявить закономерность.
Метод – укрупнение интервалов и расчет среднего уровня
-
Год
Уровень
Новые периоды
Новые уровни
1
40,6
1
43,9
2
41,5
3
49,5
4
43,6
2
41,2
5
39,2
6
40,7
7
38,2
3
37,6
8
36,5
9
38,0
10
38,7
4
39,1
11
39,4
Тенденция изображена в виде ступенчатого графика (в приложении).
Сезонные колебания:
-
Месяц
Годы
Ср. уровень за каждый месяц
Индекс сезонности
1998
1999
2000
1
242
254
249
248,3333
81,24318
2
236
244
240
240
78,5169
3
284
272
277
277,6667
90,83969
4
295
291
293
293
95,85605
5
314
323
331
322,6667
105,5616
6
328
339
344
337
110,2508
7
345
340
353
346
113,1952
8
362
365
364
363,6667
118,9749
9
371
373
369
371
121,374
10
325
319
314
319,3333
104,4711
11
291
297
290
292,6667
95,747
12
260
252
258
256,6667
83,96947
Индекс сезонности:
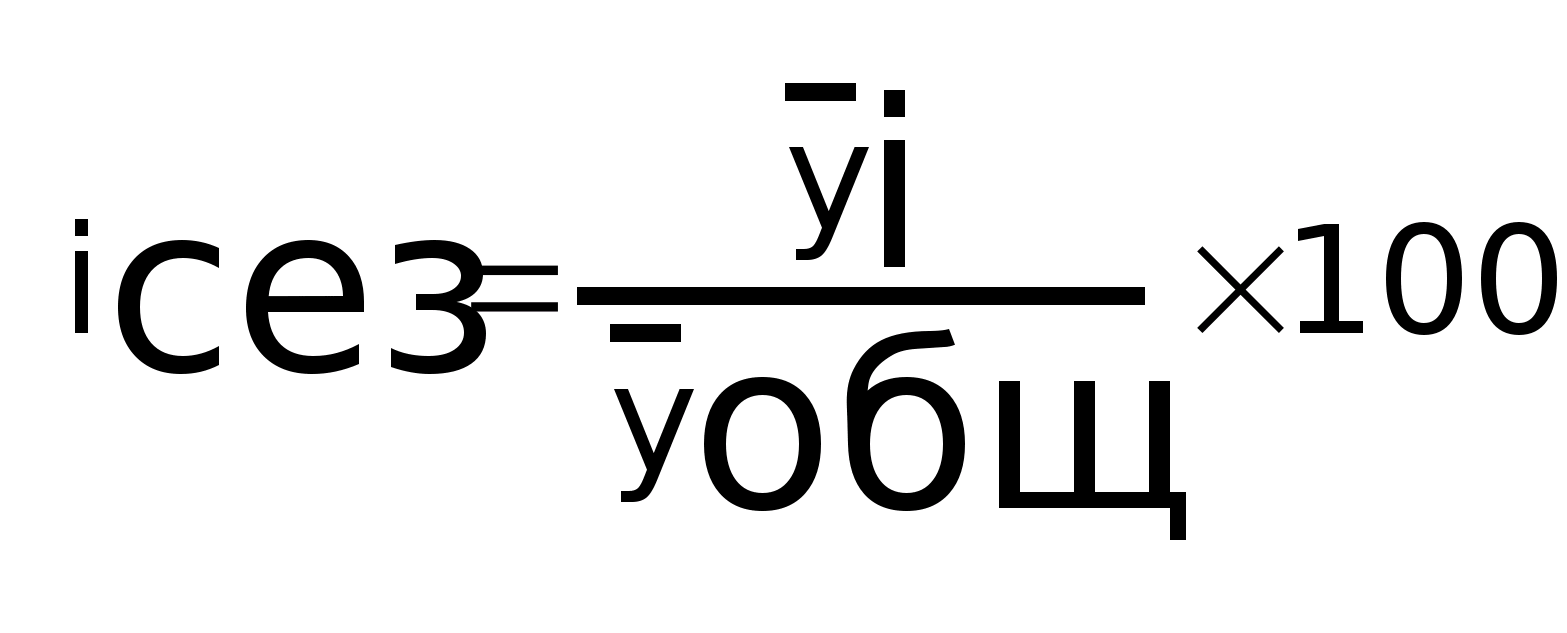 График «Сезонная
волна» в приложении.
График «Сезонная
волна» в приложении.
3. Индексы
|
Товар –представитель |
базисный год 1999 |
текущий год 2000 |
стоимость pq |
p>0>q>1> |
p>1>q>0> |
|||
|
цена |
объем |
цена |
объем |
базис.год |
текущ.год |
|||
А |
12,5 |
420 |
10,7 |
462 |
5250 |
4943,4 |
5775 |
4494 |
|
Б |
3,2 |
2540 |
4,5 |
2405 |
8128 |
10822,5 |
7696 |
11430 |
|
В |
45,7 |
84 |
55,3 |
97 |
3838,8 |
5364,1 |
4432,9 |
4645,2 |
|
Г |
83,5 |
156 |
82,5 |
162 |
13026 |
13365 |
13527 |
12870 |
|
p>0> |
q>0> |
P>1> |
q>1> |
p>0>q>0> |
p>1>q>1> |
p>0>q>1> |
p>1>q>0> |
|
|
Итого |
|
|
|
|
30242,8 |
34495 |
31430,9 |
33439,2 |
Индивидуальные индексы:
|
Товар |
i>p> |
i>q> |
А |
85,6 |
110 |
|
Б |
140,625 |
94,68504 |
|
В |
121,0065646 |
115,4762 |
|
Г |
98,80239521 |
103,8462 |
Расчет индивидуальных индексов ведется по формулам:
i>p>>
> =
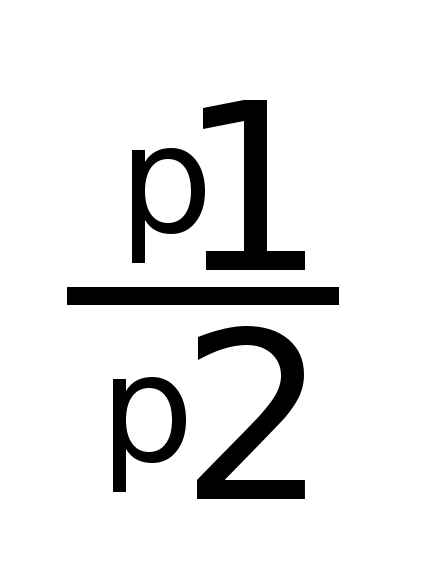 ; i>q
> =
; i>q
> =
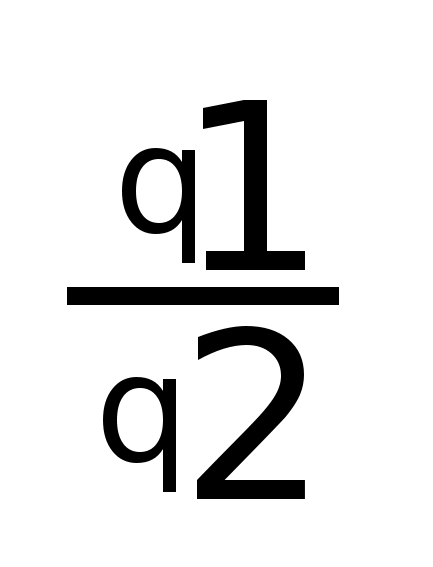
Общий индекс физического объема:
I>q>
=
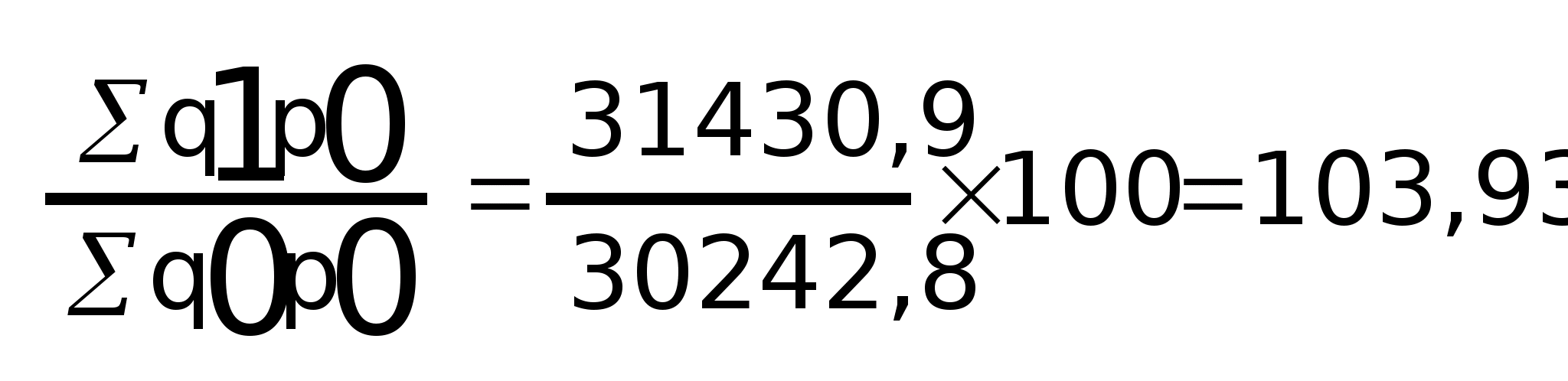
Общий индекс цен:
1)
I>p>
=
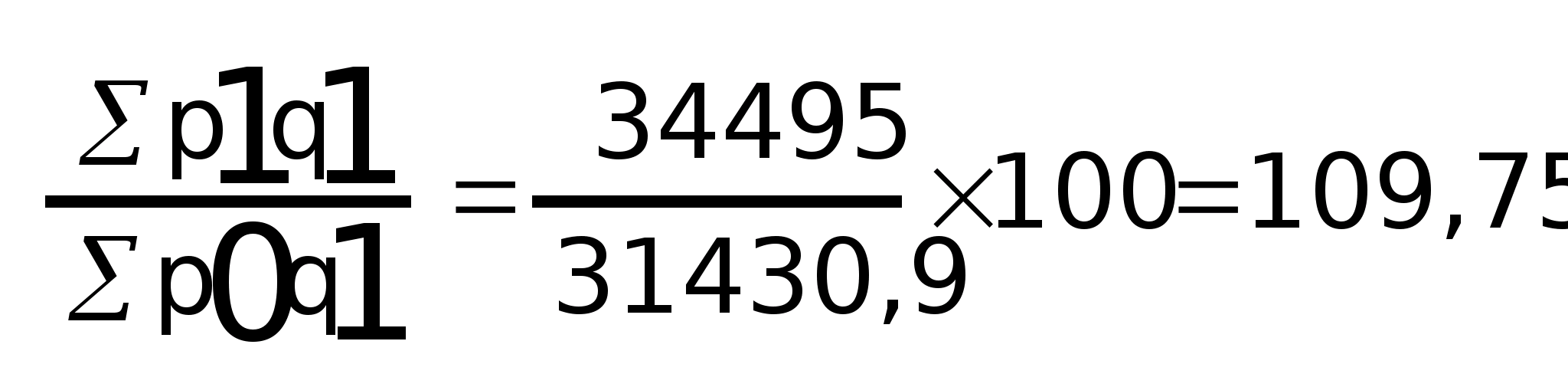
2)
I>p>
=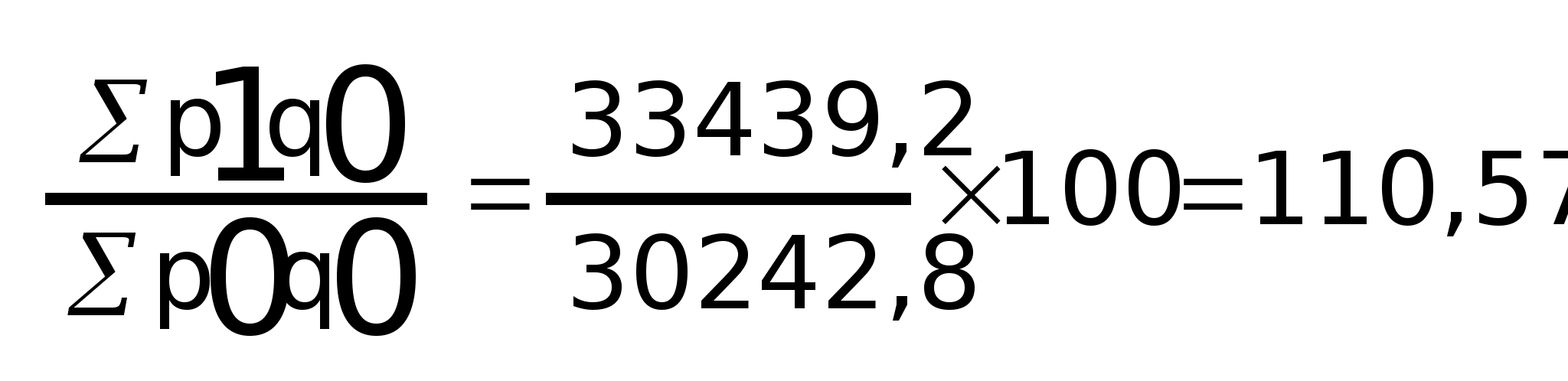
3)
I>p(>>фишер>>)>
=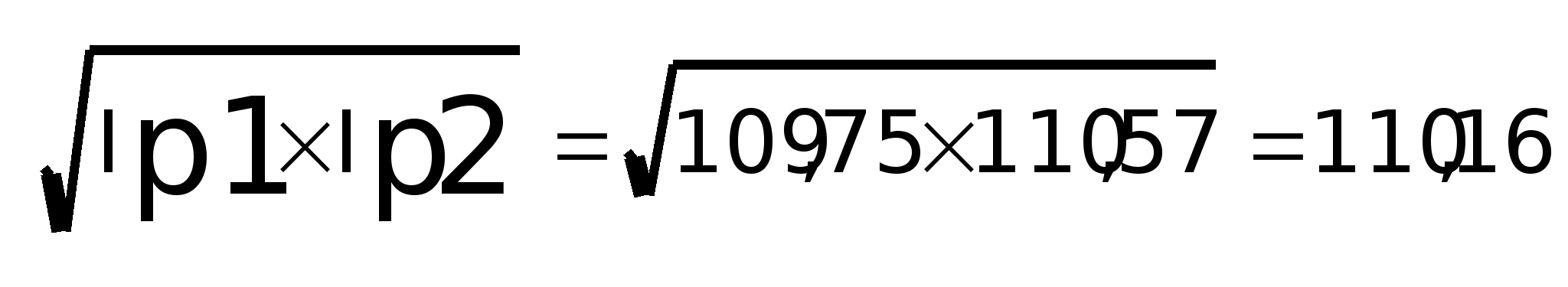
Общий индекс стоимости:
I>pq>
=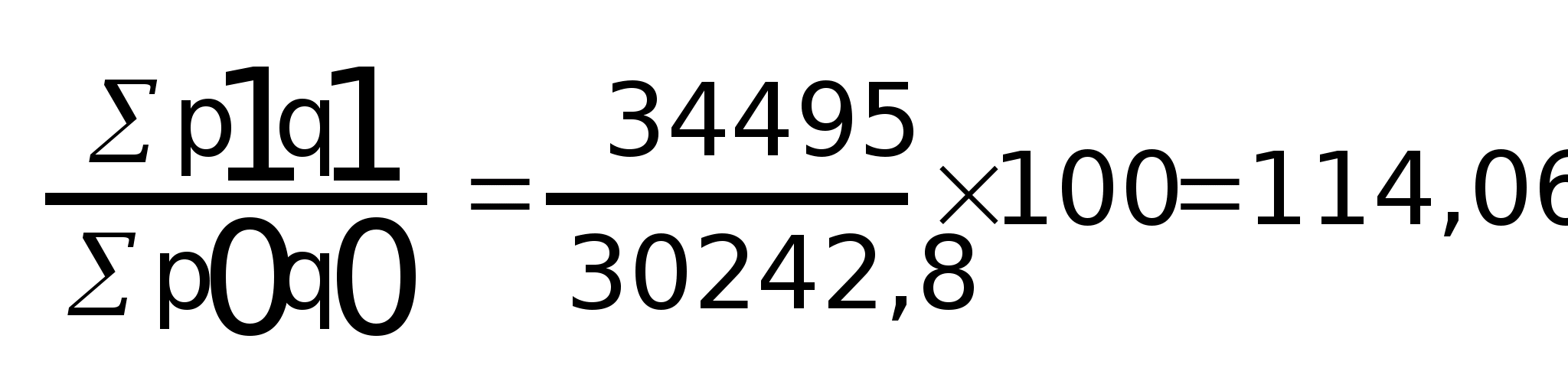
Взаимосвязь индексов I>p> , I>q> , I>pq> :
I>p> x I>q> = I>pq>
(1,0975 x 1,0393) x 100 = 114,06
Влияние факторов на изменение стоимости:
Общее изменение стоимости составило:
 pq
=
pq
=
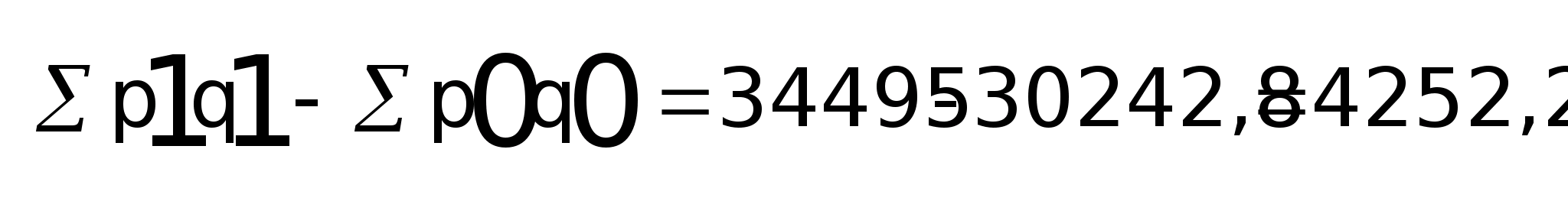
в том числе :
- за счет роста цен на 9,75% дополнительно получено доходов:
 p
=
p
=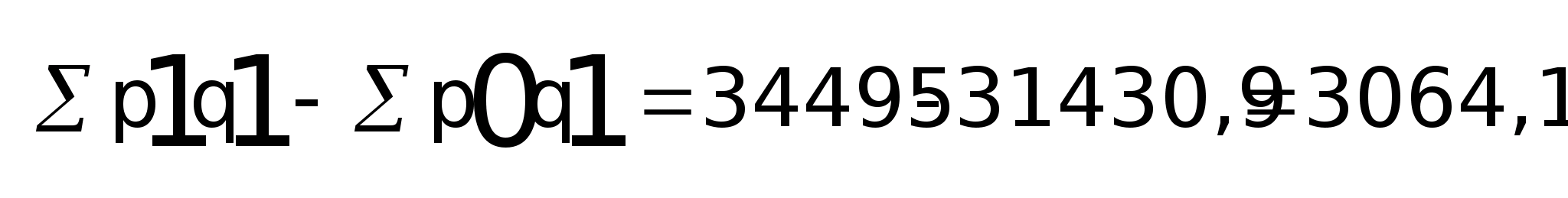
- за счет роста физического объема продаж на 3,93% дополнительные доходы получены в размере:
 q
=
q
=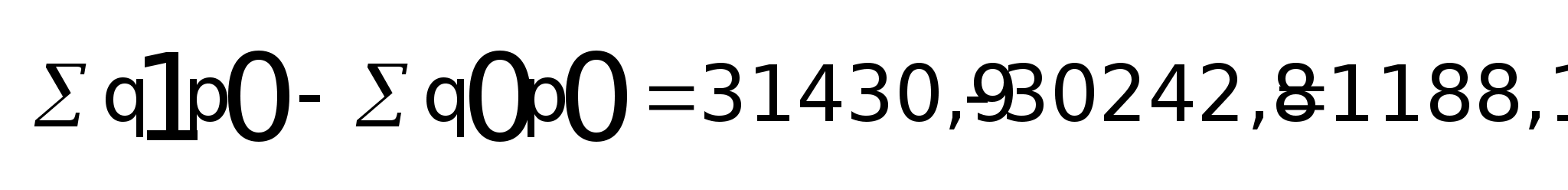
Взаимосвязь
 p,
p,
 q,
q,
 pq
:
pq
:
 pq
=
pq
=
 p
+
p
+
 q
q
4252,2 = 3064,1 + 1188,1
Методика преобразования общих индексов в среднюю из индивидуальных:
Общие
индексы – это относительные величины,
в то же время, общие индексы являются
средними из индивидуальных индексов,
т.е. индивидуальный индекс i
x,
а Y
 .
Вид общего индекса должен соответствовать
агрегатной форме расчета. В этом случае
сохраняется экономический смысл индекса
и меняется только методика расчета.
.
Вид общего индекса должен соответствовать
агрегатной форме расчета. В этом случае
сохраняется экономический смысл индекса
и меняется только методика расчета.
Алгоритм :
1. Индекс физического объема
а) индивидуальный индекс физического объема:
i>q
> =
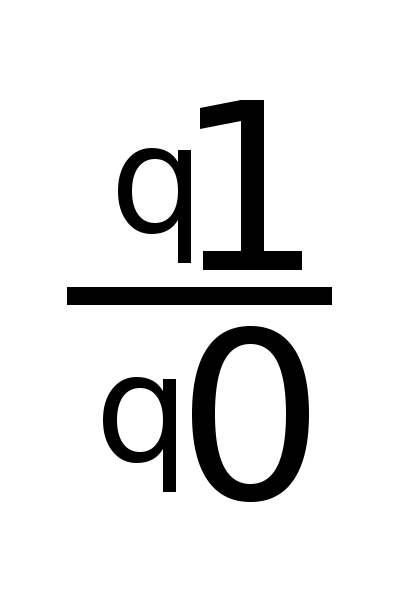
|
Товар i>q> А110 Б 94,68504 В 115,4762 Г 103,8462 |
I>q>
=
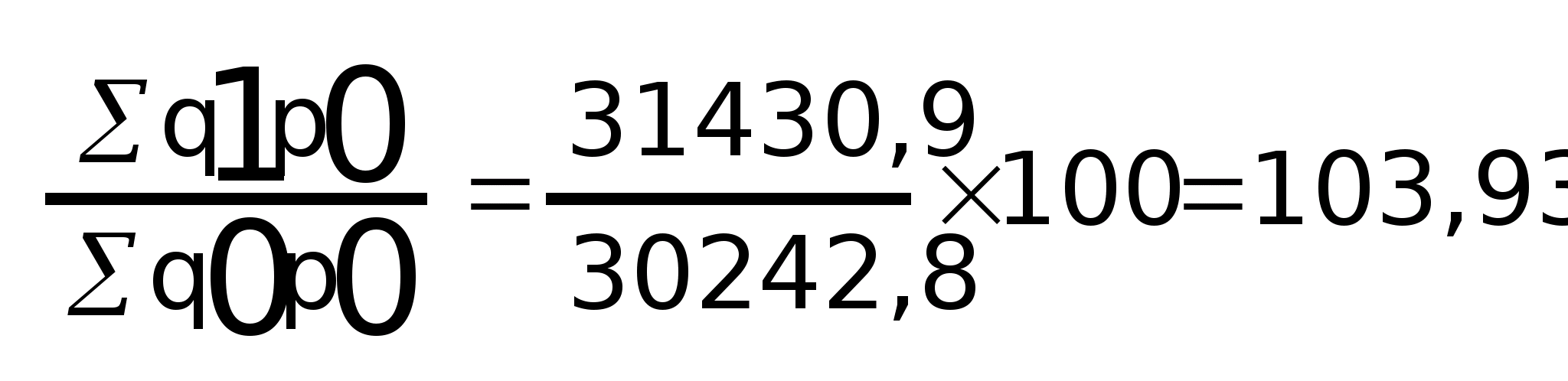
в)
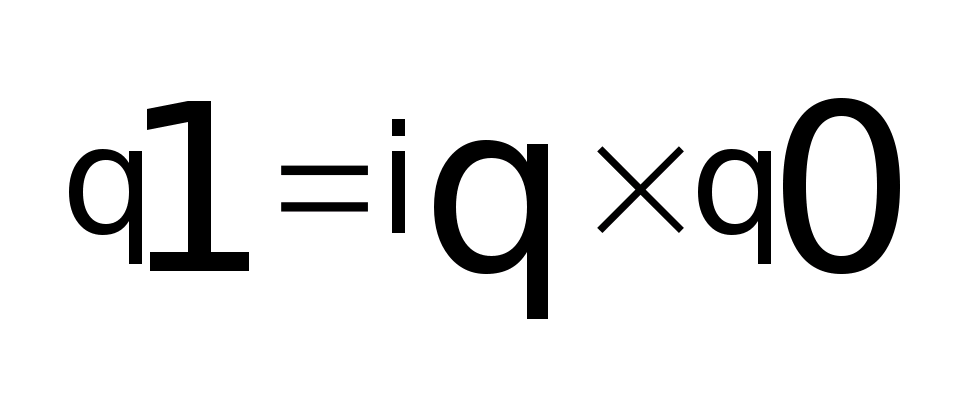
г)
I>q>
=
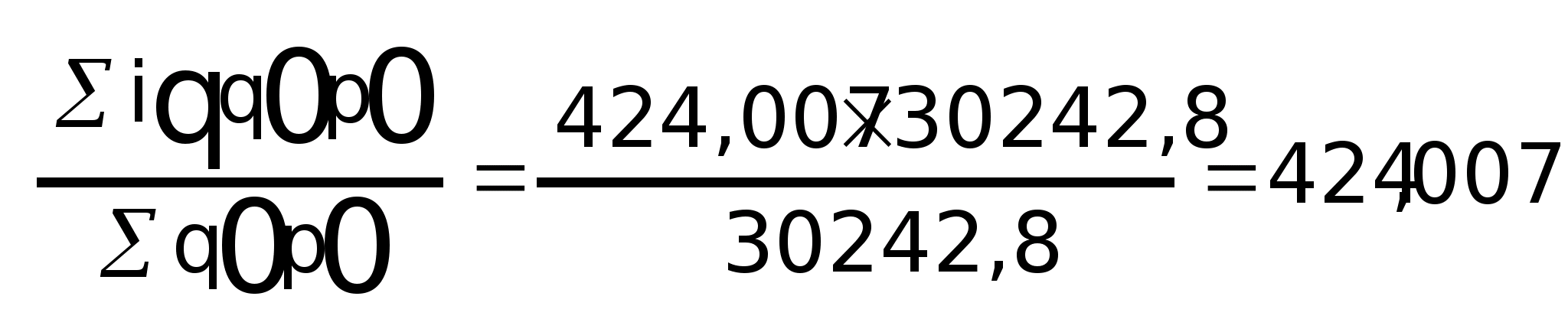
i>q >x (q>0>p>0>) f
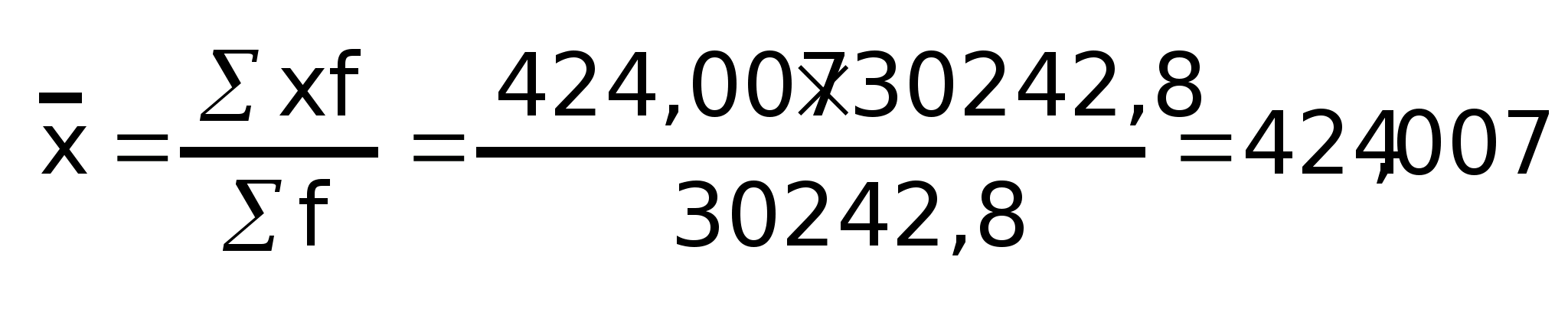
Таким образом, индекс физического объема представляет собой среднюю арифметическую из индивидуальных индексов, взвешенных по стоимости продукции базового периода.
2.
Индекс цен Ласпейреса I>p>
=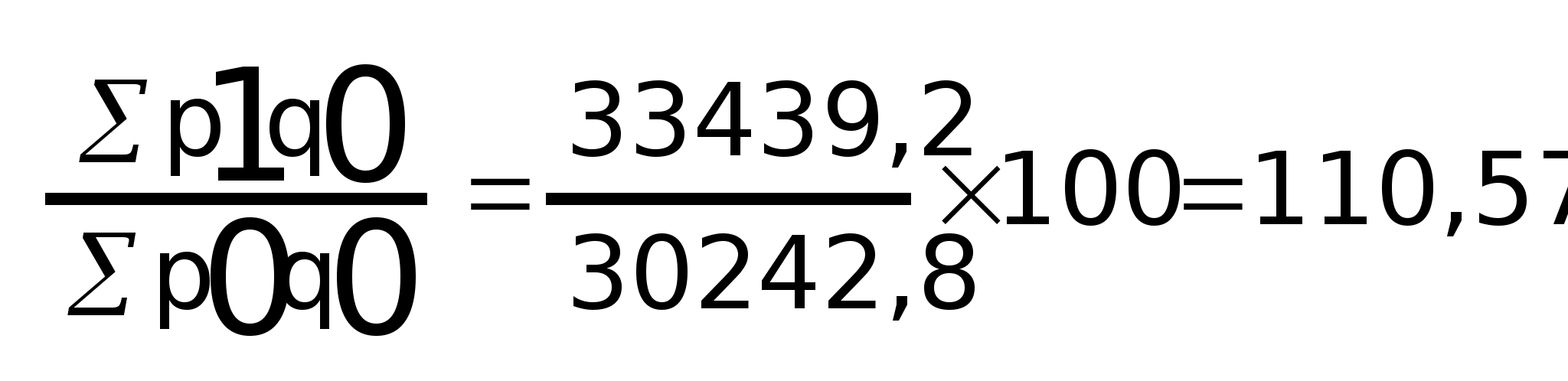 i>p>>
> =
i>p>>
> =
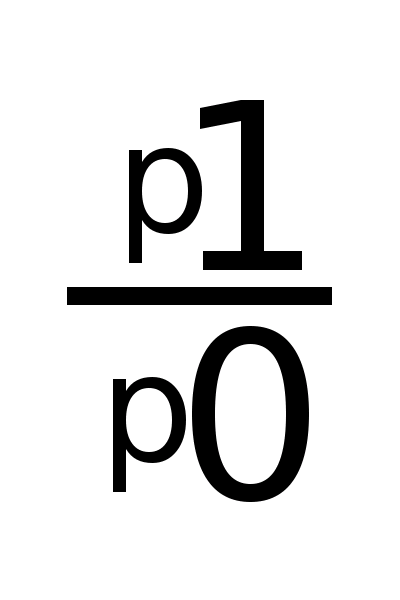
|
Товар |
i>p> |
А |
85,6 |
|
Б |
140,625 |
|
В |
121,007 |
|
Г |
98,802 |
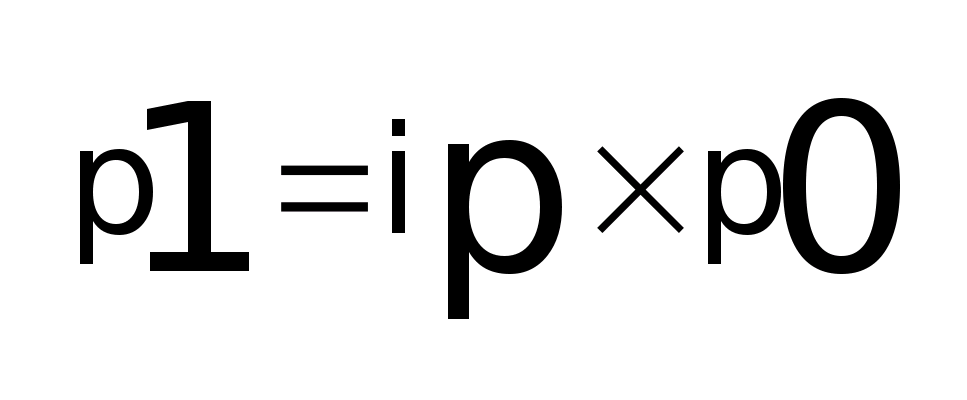
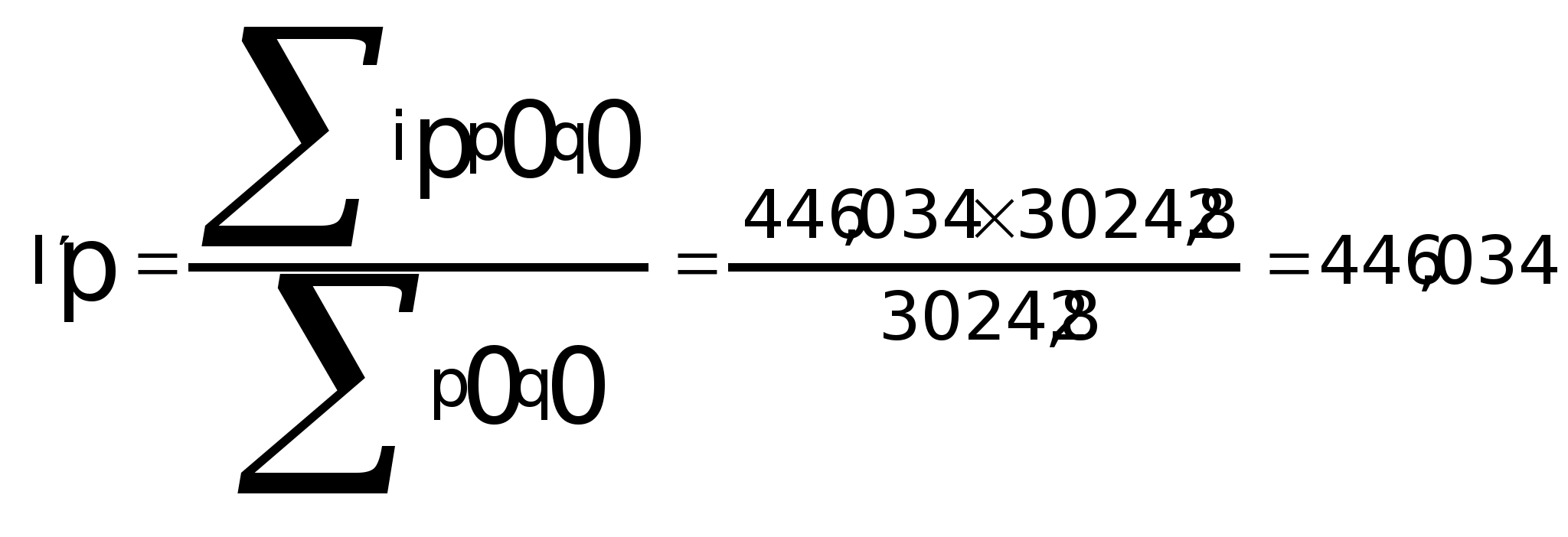
Индекс цен Ласпейреса – это средняя арифметическая из индивидуальных индексов, взвешанных по стоимости базового периода или удельному весу.
3. Индекс цен Пааше
а) Индивидуальный индекс цены
i>p>>
> =
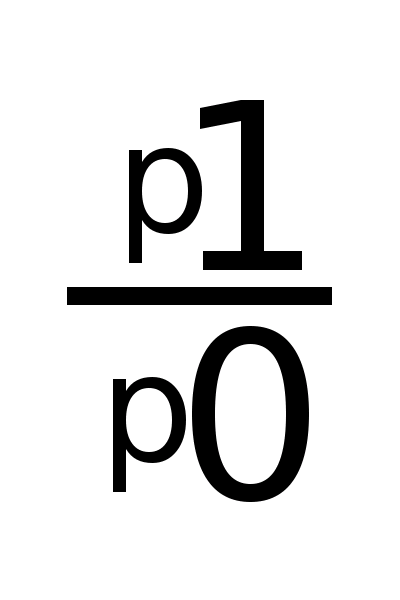 б)
I>p>
=
б)
I>p>
=
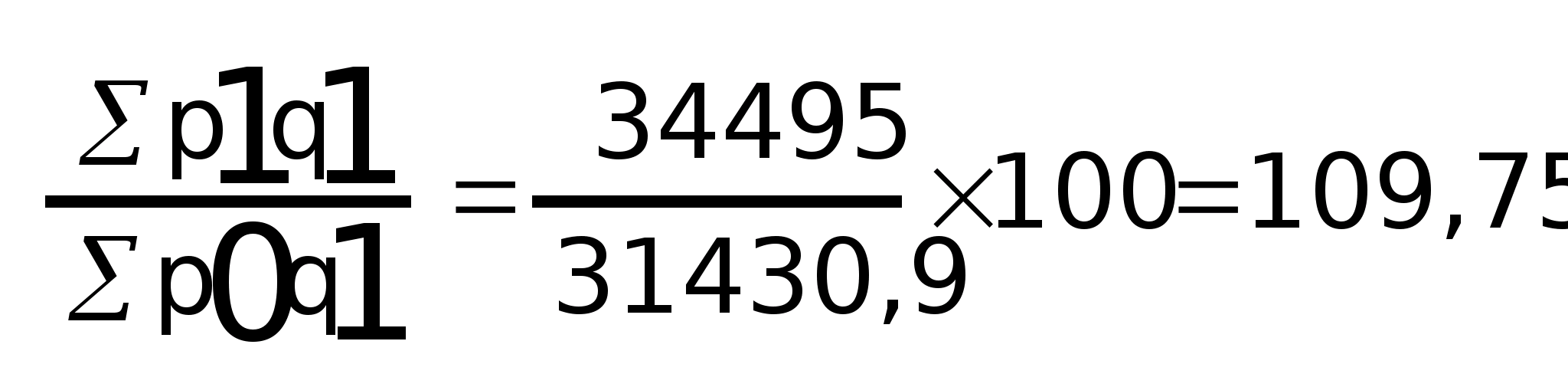 в) p>0
> =
в) p>0
> =
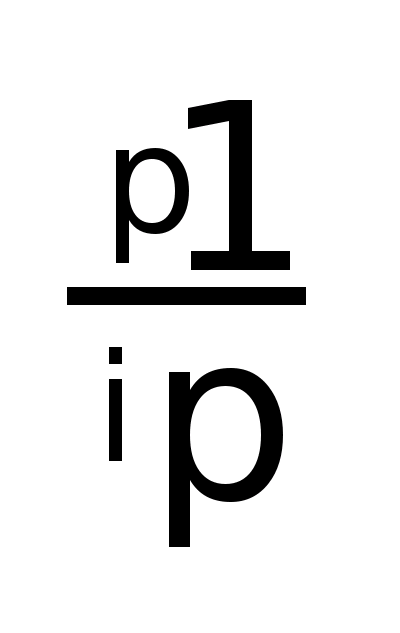 I>p>
=
I>p>
=
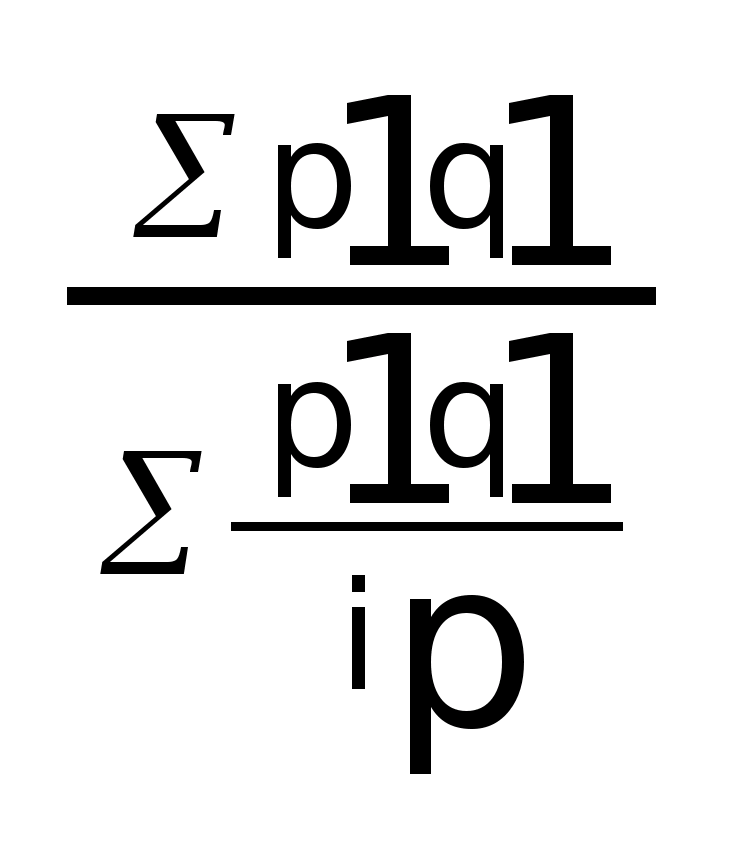 Индекс
цен Пааше является средней гармонической
величиной из индивидуальных индексов,
взвешенных по стоимости текущего
периода.
Индекс
цен Пааше является средней гармонической
величиной из индивидуальных индексов,
взвешенных по стоимости текущего
периода.
7вопрос Относительные величины
Статистика широко применяет относительные величины, потребность в которых возникает на стадии обобщения. Они помогают установить закономерности, в них заключен «молчаливый вывод»; являются самостоятельными статистическими показателями и имеют самостоятельную широкую сферу применения, например, уровень рождаемости, естественного прироста населения, рентабельность и т.д.
Относительная величина – это статический показатель, полученный путем сопоставления двух других величин (абсолютных, средних и других относительных).
При пользовании относительными величинами следует применять достаточное для целей исследования число значащих цифр. Поэтому существуют различные способы выражения относительных величин. Если сравниваемая величина больше базы y>1> > y>0>, то удобно пользоваться коэффициентом К = у>1>/у>0>. Если между уровнями у>1> и у>0> различия абсолютных величин невелики, то удобно применять децили и проценты: Δ = 10 (у>1>/у>0>); Т = 100 (у>1>/у>0>). Если уровень у>1> значительно меньше базы, то удобно применять промилле и продецимилле: П = 1000 (у>1>/у>0>); П´ = 10000 (у>1>/у>0>).
Например, рост цен может быть измерен и коэффициентом, и процентом (рост в 2,1 раза или 103,15%), рождаемость и естественный прирост определяют на 1000 чел. населения и т.д.
2.2. Виды относительных величин
В зависимости от характера сравниваемых абсолютных величин можно выделить два типа относительных величин. Если сравниваются две абсолютные величины, имеющие одинаковые единицы измерения, то относительная величина показывает «отношение» и является безразмерной. Если сравниваются две абсолютные величины, у которых единицы измерения не совпадают, то относительные величины имеют размерность.
Относительная величина структуры определяется как отношение числа единиц f или значения признака у изучаемой части к общему числу Σf: W = f / Σf;
Относительная величина координации показывает отношение численности единиц одной части совокупности к численности единиц другой.
Изменение уровня изучается во времени относительной величиной динамики. Например, уровень показателя 1999 г. (у>1>) сравнивается с уровнем того же показателя по тому же объекту 1990 г. (у>0>): К>1> = у>1>/у>0>.
Прогнозируемый уровень сравнивается с существующим – относительная величина прогноза: К>пр> = у>пр>/у>0>.
Изменение уровня изучается по сравнению с предварительным прогнозом (нормой, планом) – относительная величина выполнения прогноза: К>в. пр>. = у>1>/у>пр>.
Относительная величина интенсивности представляет собой сравнение двух разных статических показателей, которые имеют размерность. К таким показателям относится плотность населения, автомобильных дорог и т.д.
Относительными величинами также являются индексы: биржевые, социальные, сезонности и т.д.
i>р> = р>1>/р>0>; i>q> = q>1>/q>0>; i>z>> >= z>1>/z>0> и т.д.
Тема 3. Средние величины и показатели вариации
3.1. Сущность и значение средних величин
Средняя величина отражает типичные размеры признака, характеризует качественные особенности явлений в количественном выражении.
Средние характеризуют одной величиной значение изучаемого признака для всех единиц качественно однородной совокупности.
К. Маркс отметил: «Средняя величина – всегда средняя многих различных индивидуальных величин одного и того же вида».
Средняя величина – величина абстрактная, потому что характеризует значение абстрактной единицы, а значит, отвлекается от структуры совокупности.
Понятие степенной средней, формула расчета, виды средних величин и область их применения, правило мажорантности средних
Степенная
средняя – это такая величина, которая
рассчитана по индивидуальным значениям
признака, возведенным в степень К,
и приведена к линейным размерам:
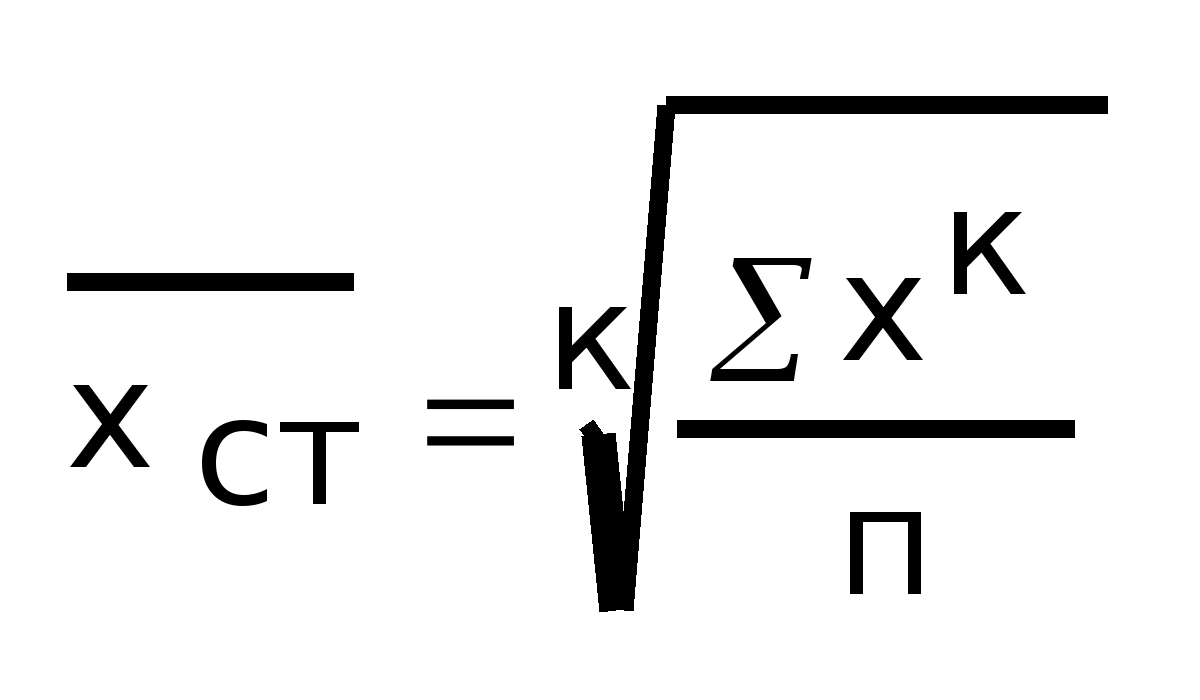
В зависимости от показателя степени К средняя может быть гармонической (К = -1), арифметической (К = 1), геометрической (К = 0), квадратической (К = 2), кубической (К = 3), биквадратической (К = 4). Каждая средняя обладает определенными свойствами и имеет свою сферу применения.
Е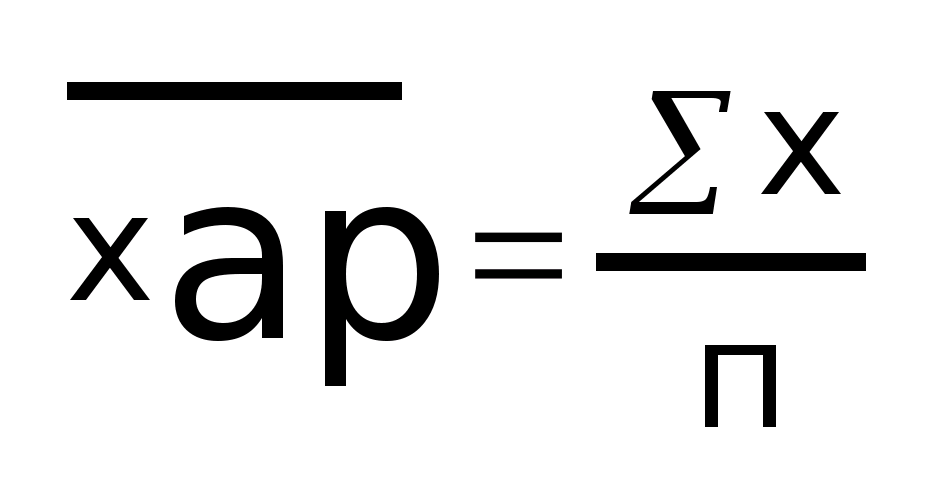
сли
К
= 1, то средняя является арифметической:
где n - число наблюдений.
Массовые
по численности совокупности обобщаются
в виде ряда распределения. Характер
распределения, частота повторения
каждого признака оказывает влияние на
среднюю, которая называется средней
взвешенной:
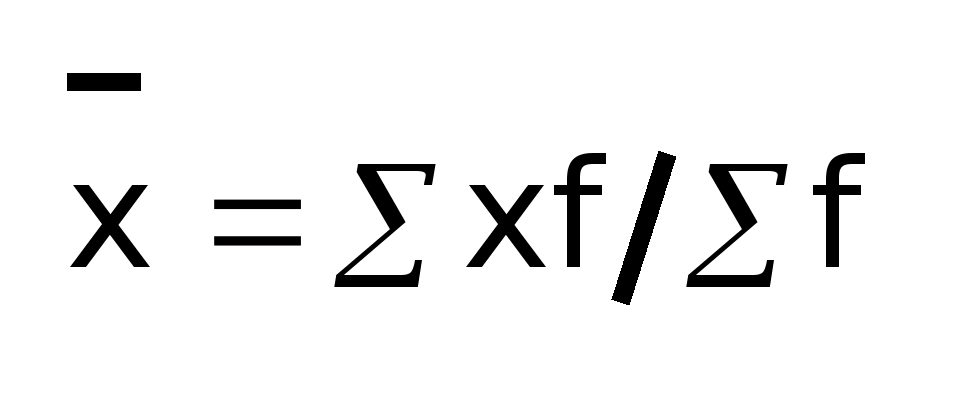
где f - частота повторения признака (статический вес).
Если
К
= -1, средняя является гармонической. Это
величина, обратная простой средней
арифметической:
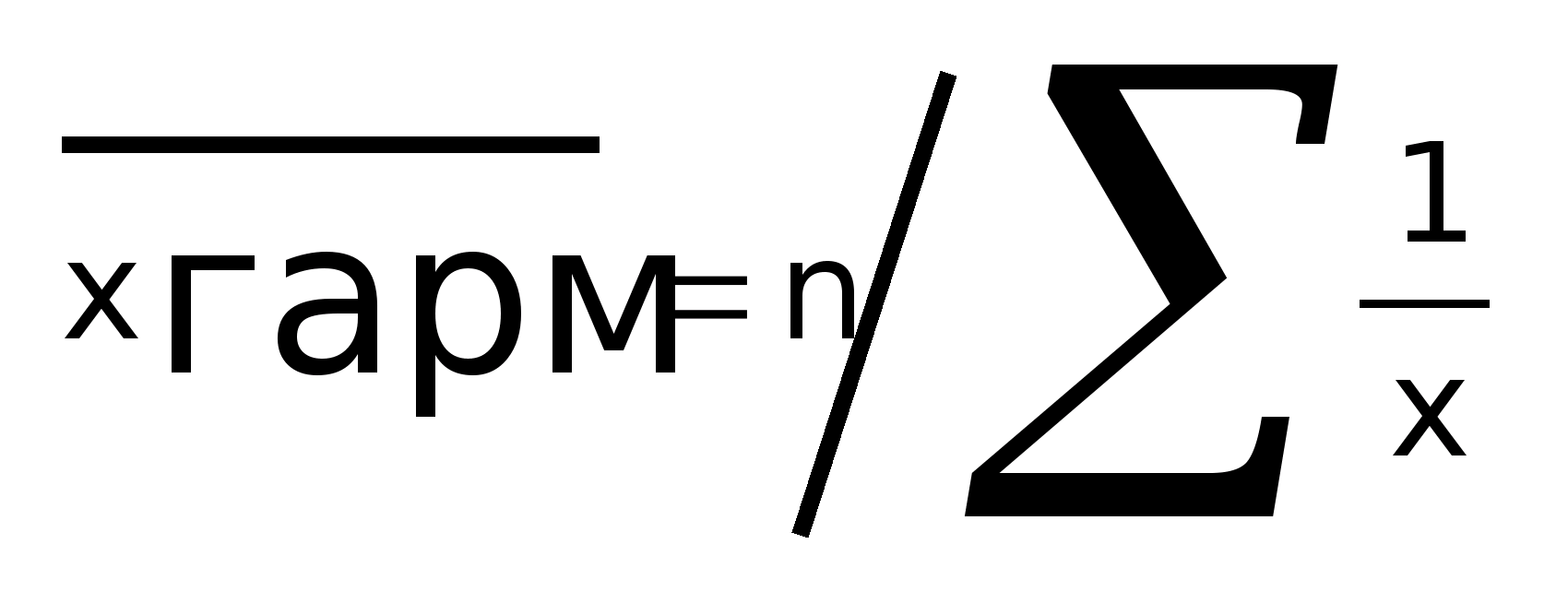
Средняя
гармоническая взвешенная определяется:
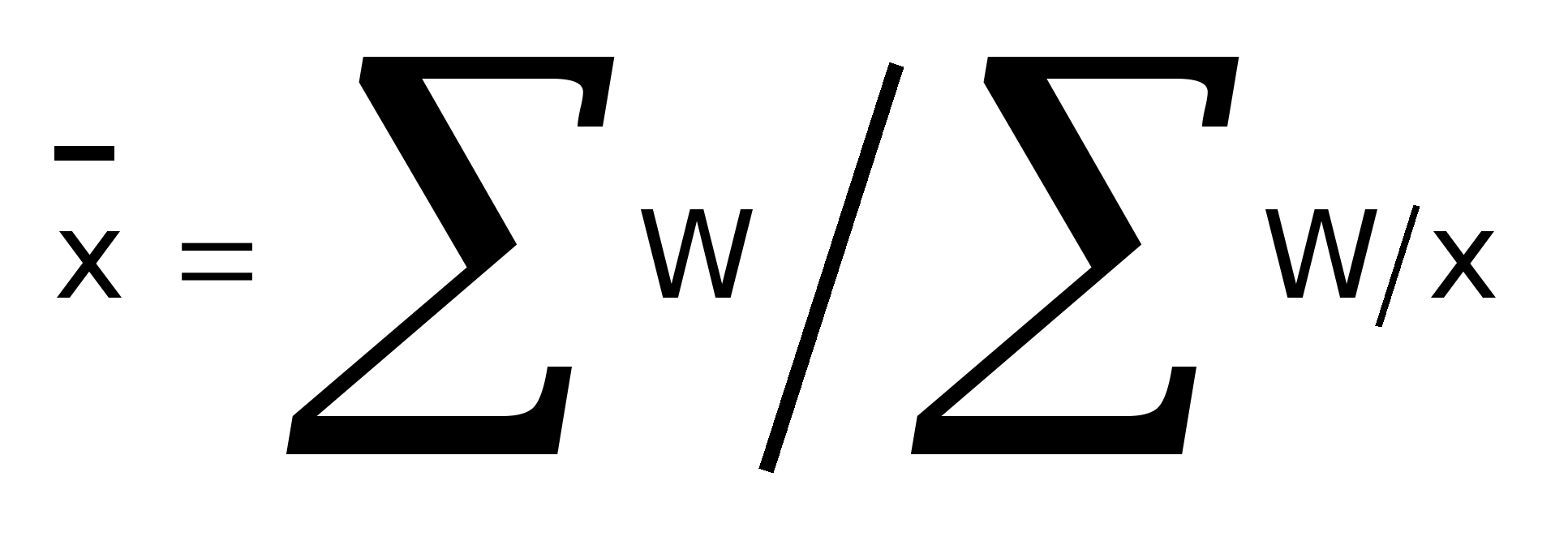
где ΣW - суммарное значение признака.
Если К = 0, то средняя является геометрической. Эта величина, полученная как корень m-й степени из произведения значений признака:
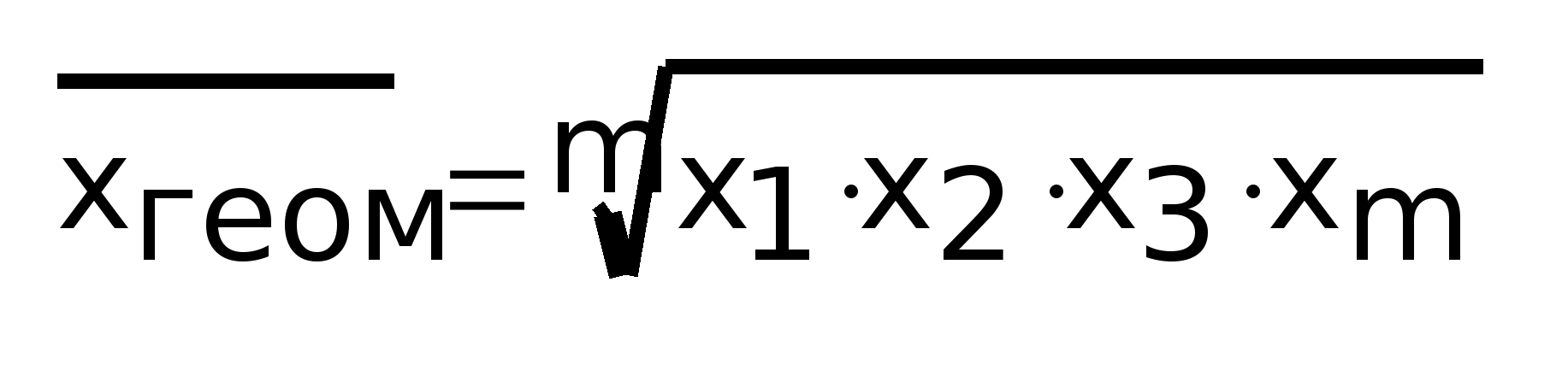
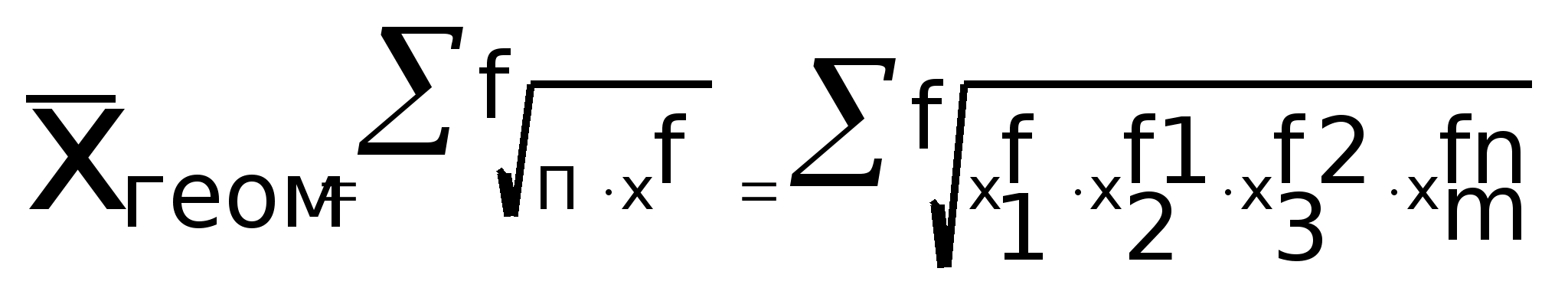
Взвешенная -
Если К = 2, то средняя является квадратичной:
Простая - 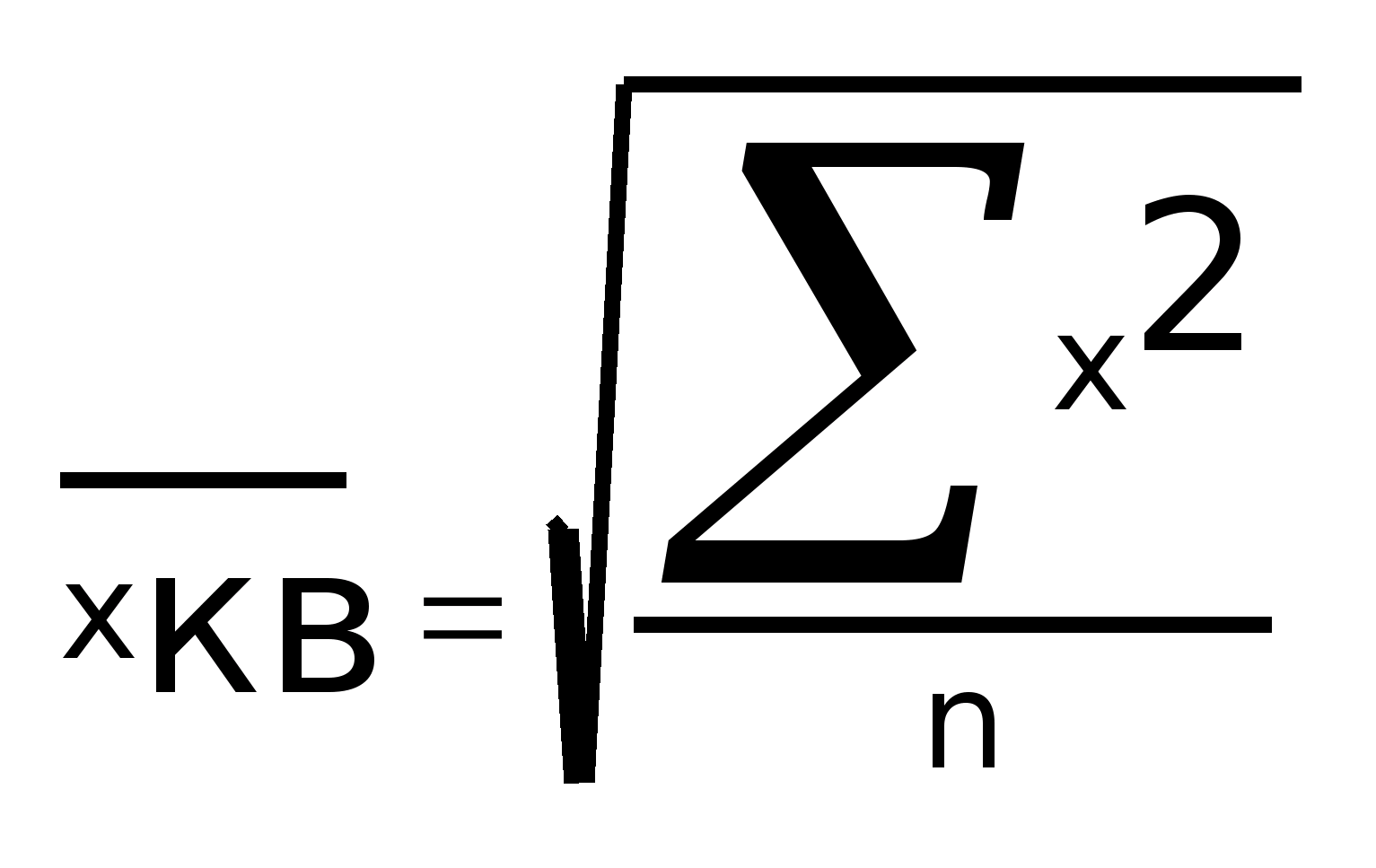
Взвешенная - 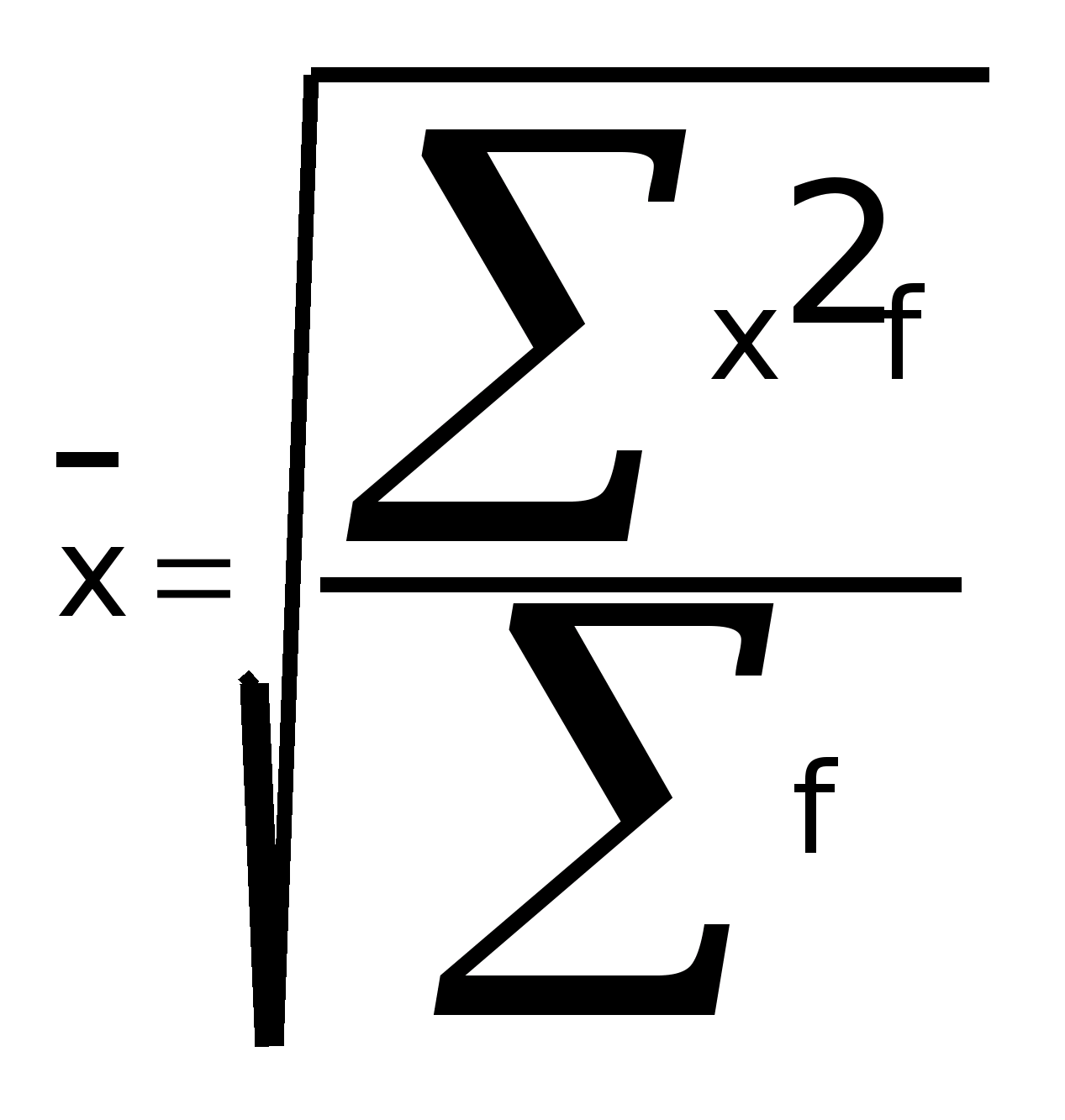
и т.д.
Если
для одного и того же первичного ряда
вычислить различные степенные средние,
то чем больше показатель степени К,
тем больше абсолютное значение средней:
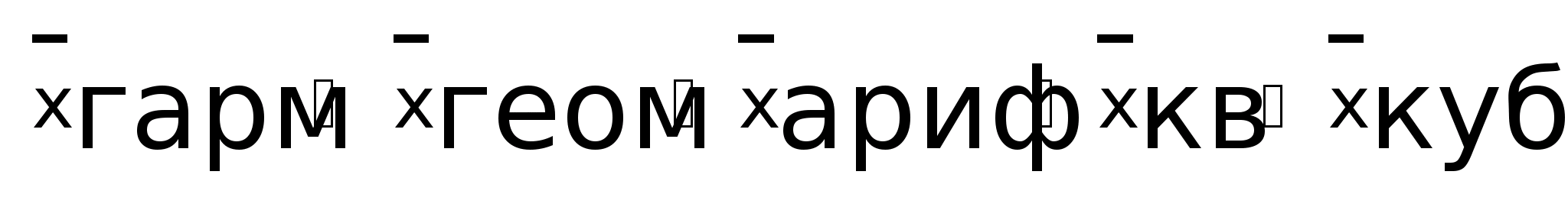
Правило называется мажорантности степенных средних.
3.3. Свойства средней арифметической
Средняя величина арифметическая обладает рядом свойств, позволяющих ускорить расчет.
Она не изменяется, если веса всех вариантов умножить или разделить на одно и то же число.
Если все значения признака одинаковые, то средняя равна этой же величине.
Средние суммы или разности равны сумме или разности средней:
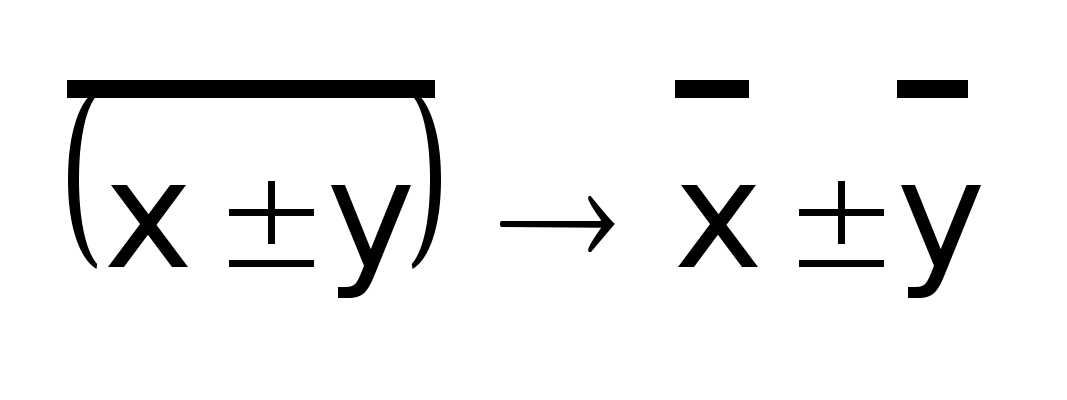
Если из всех значений Х вычесть постоянную величину С, то средняя уменьшается на это значение.
Если все значения уменьшить в d раз (Х/d), то средняя уменьшится в d раз.
Сумма отклонений значения признака равна 0.
Сумма
квадратов отклонений
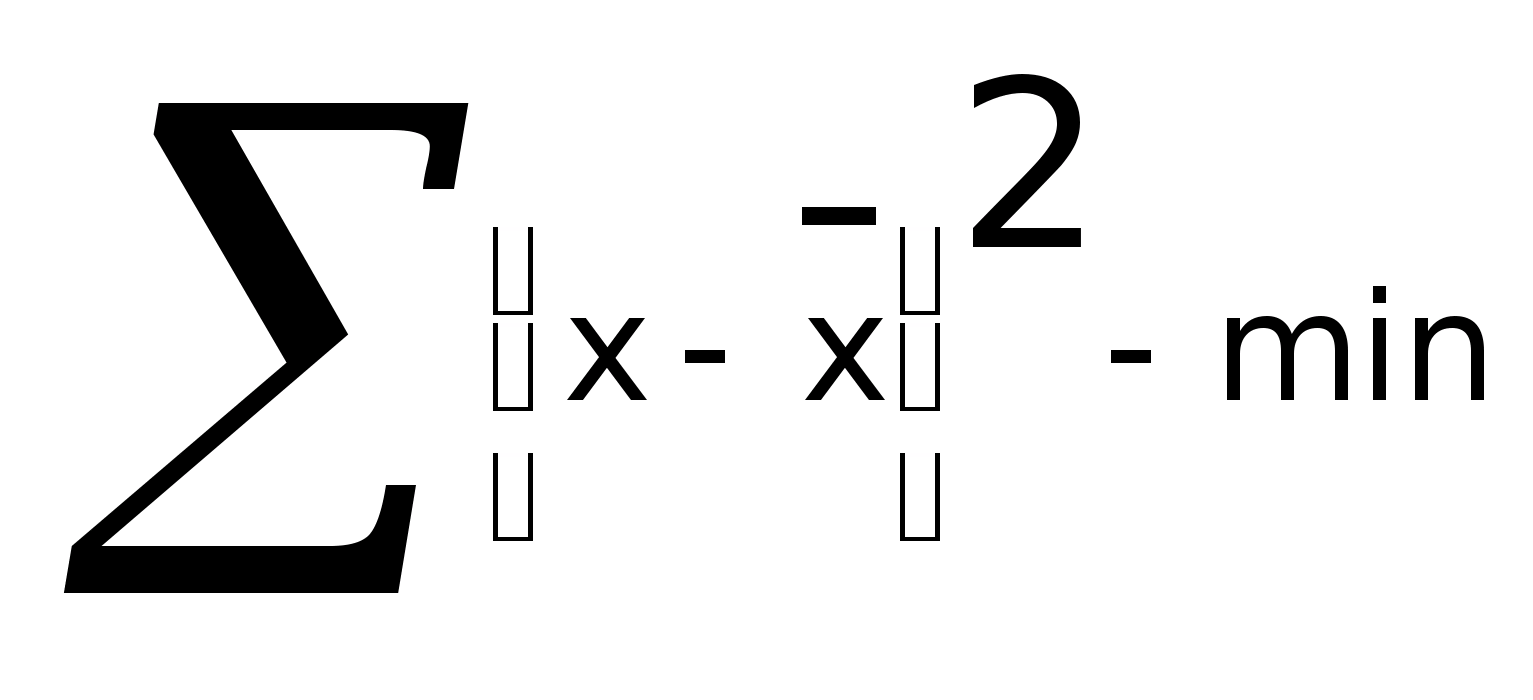
3.4. Расчет моды и медианы
Модой (М>0>) называется чаще всего встречающийся вариант или то значение признака, которое соответствует максимальной точке теоретической кривой распределения.
В дискретном ряду мода – это вариант с наибольшей частотой. В интервальном вариационном ряду мода приближенно равна центральному варианту так называемого модального интервала.
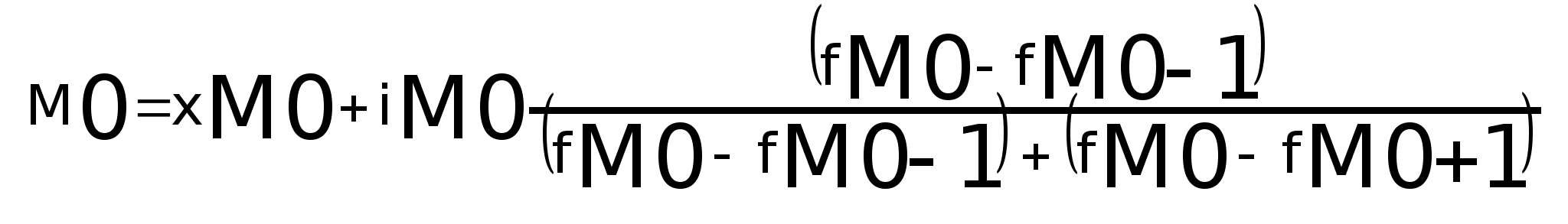
где х>М0> - нижняя граница модального интервала;
i>M>>0> - величина модального интервала;
f>M>>0> - частота, соответствующего модального интервала;
f>M>>0-1> - частота, предшествующая модальному интервалу;
f>M>>0+1> - частота интервала, следующего за модальным.
Медиана (М>е>) – это величина, которая делит численность упорядоченного вариационного ряда на 2 равные части: одна часть значения варьирующая признака меньшие, чем средний вариант, а другая часть – большие. Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда, а с четным числом членов медианой будет средняя арифметическая из двух смежных вариант.
В интервальном вариационном ряду порядок нахождения медианы следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал.
Медиана делит численность ряда пополам, следовательно, она там, где накопительная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Если предполагать, что внутри медианного интервала нарастание или убывание изучаемого признака происходит по прямой равномерно, то формула медианы в интервальном ряду распределения будет иметь следующий вид:
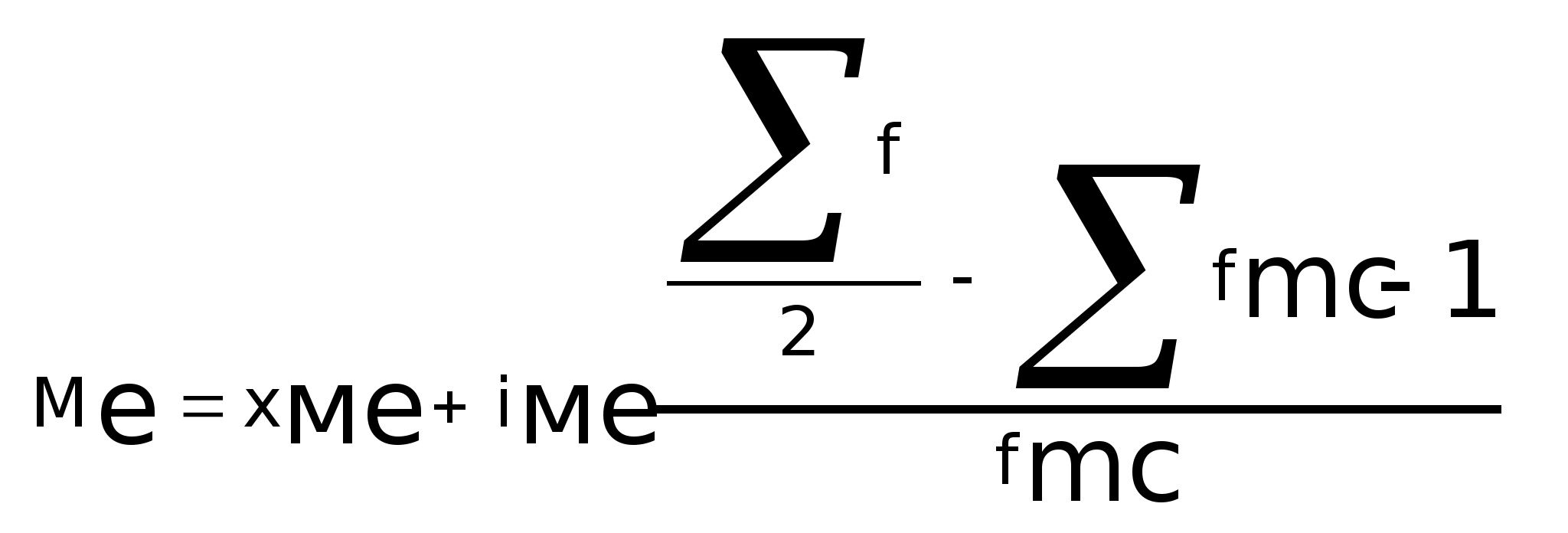
где х>ме> - нижняя граница медианного интервала;
i>me> - величина медианного интервала;
Σf/2 - полусумма частот ряда;
Σf>mе-1> - сумма накопительных частот, предшествующих медианному
интервалу;
f>mе> - частота медианного интервала.
Квартили – это значения признака, которые делят ряд на 4 равные части. Различают нижний квартиль Q>1>, медиану М>е> и верхний квартиль Q>3>.
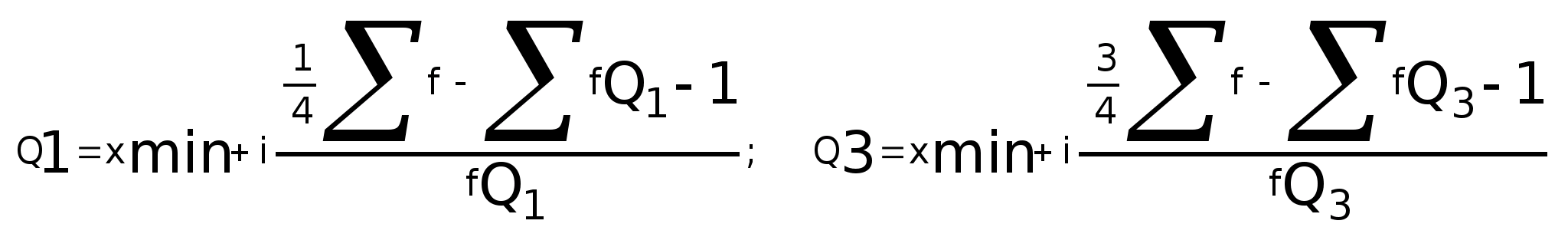
где x>min> - минимальные границы квартильных интервалов;
i - интервал ряда распределения
Σf>Qf>>-1>; Σf>Q>>3-1> - суммы частот всех интервалов, предшествующих
квартильным;
f>Q1>; f>Q3 >- частоты квартильных интервалов
Децили (D) – варианты, которые делят ранжированный ряд на 10 равных частей. Так, первый и второй децили могут быть вычислены по формулам:
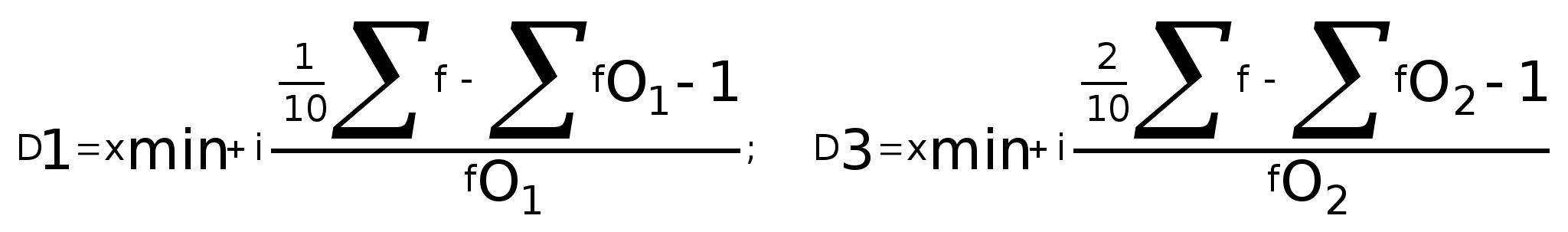
где x>min> - минимальные границы децильных интервалов;
i - интервал ряда распределения
Σf>О>>f>>-1>; Σf>О2-1> - суммы частот всех интервалов, предшествующих
децильным;
f>D>>1>; f>D>>3 >- частоты децильных интервалов
3.5. Понятие вариации признака, показатели вариации, дисперсия альтернативного признака. Упрощенный способ расчета дисперсии. Виды дисперсий в совокупности, разбитой на группы, правило сложения дисперсий
Способность признака принимать различные значения называют вариацией признака. Для измерения вариации признака используют различные обобщающие показатели – абсолютные и относительные.
Размах вариации – это разность максимального и минимального значений признака: R = х>max> - х>min>.
Среднее линейное отклонение – это средняя из абсолютных значений отклонений признака от своей средней:
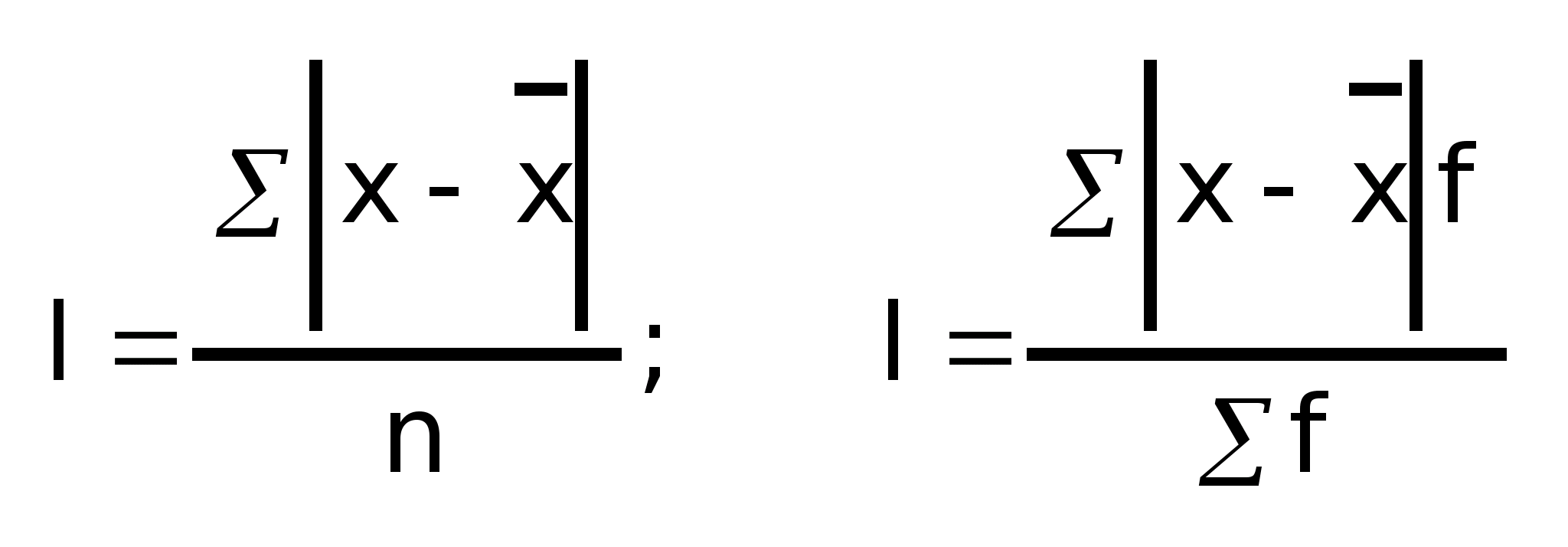
Средняя из квадратов отклонений значений признака от своей средней, т.е. дисперсия:
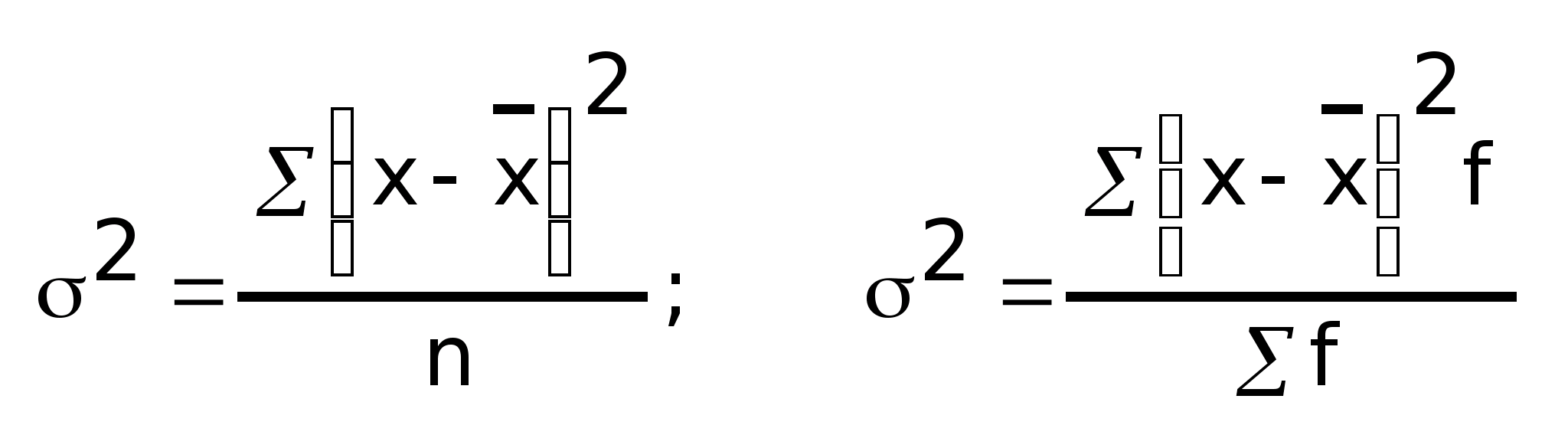
Дисперсия есть разность среднего квадрата и квадрата средней
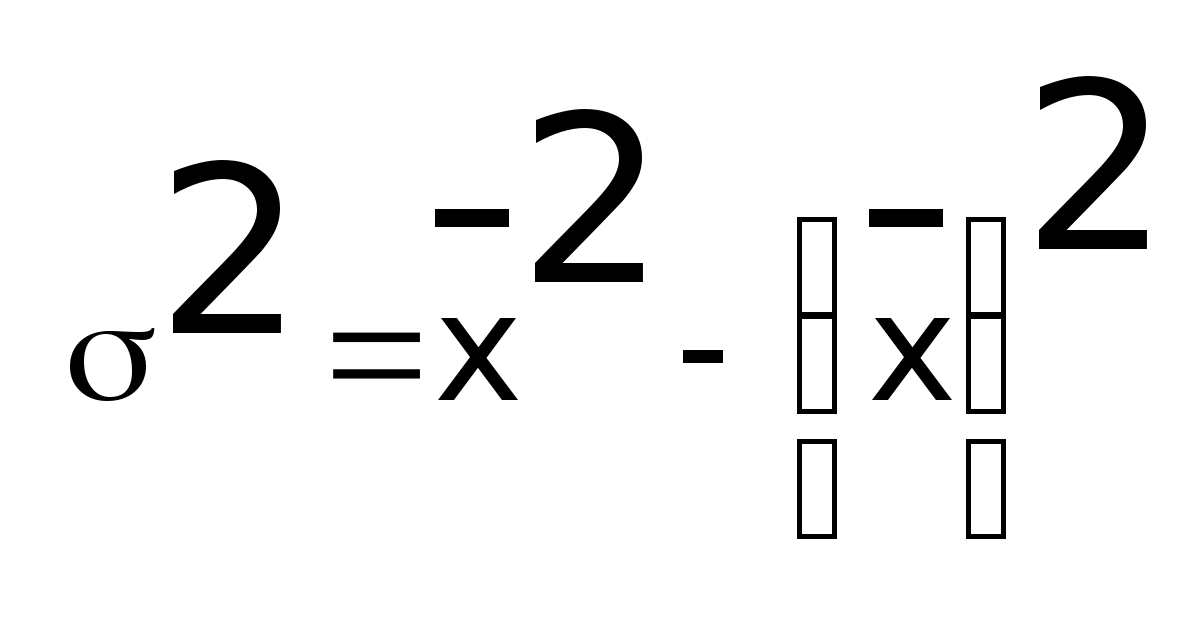
или
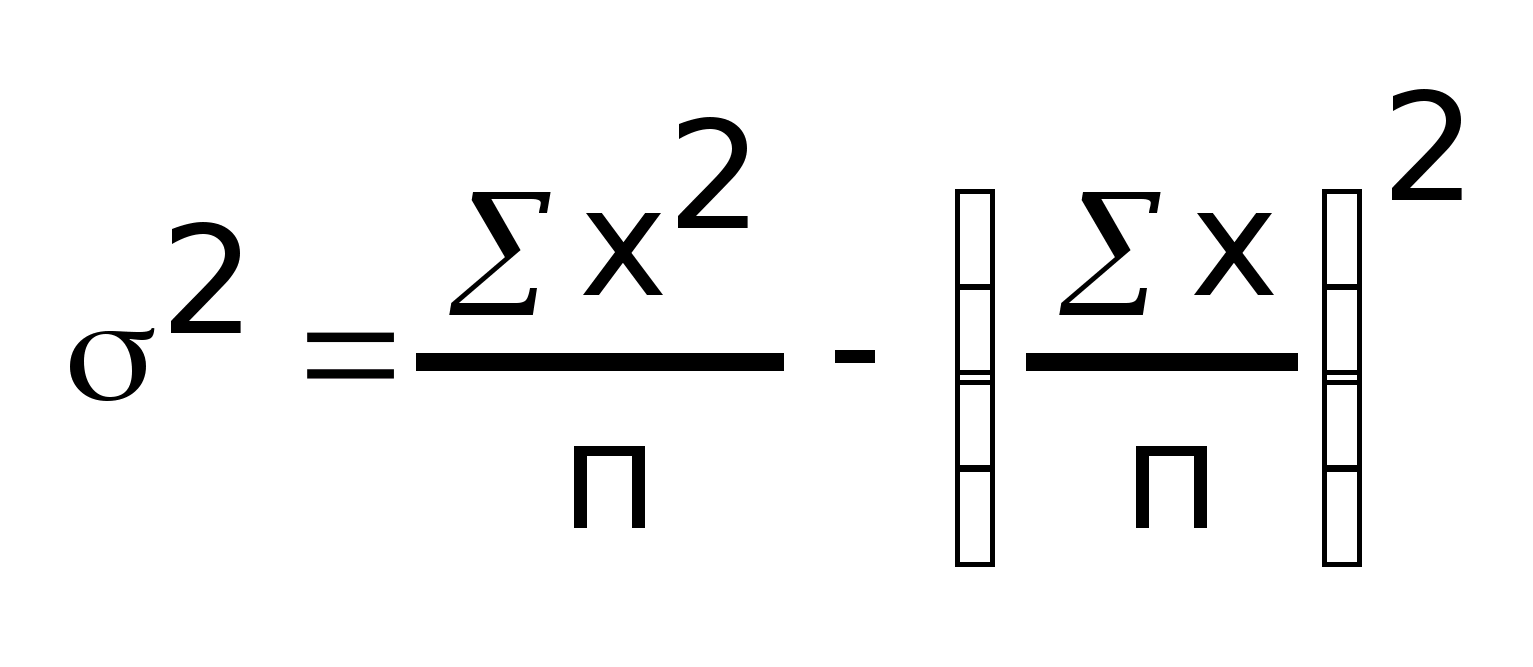 - простая
- простая
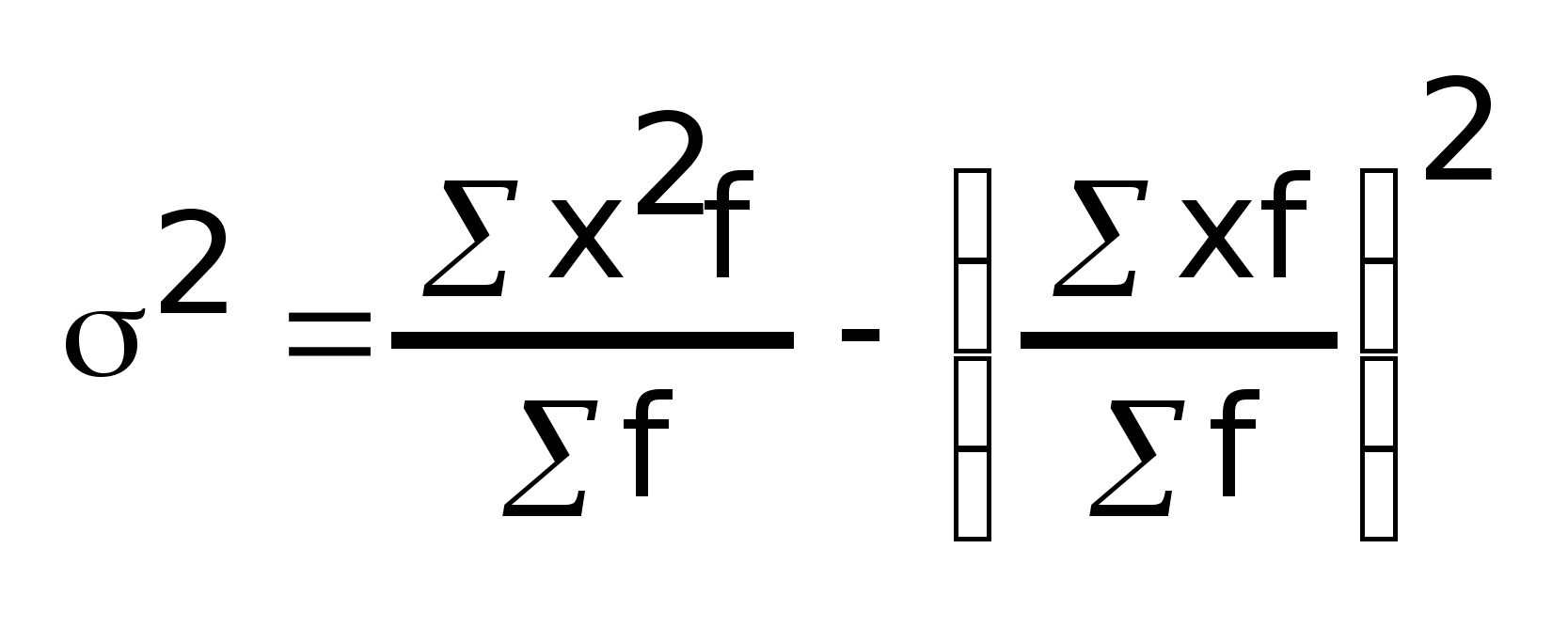 - взвешенная
- взвешенная
Дисперсия
может быть определена методом условных
моментов. Момент распределения – это
средняя m
отклонений значений признака от
какой-либо величины А:
если А
= 0, то момент называется начальным; если
А
=
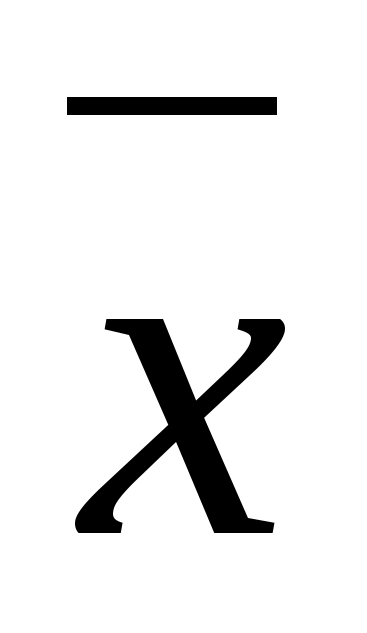 ,
то моменты – центральными; если А
= С,
то моменты – условными.
,
то моменты – центральными; если А
= С,
то моменты – условными.
В зависимости от показателя степени К, в которую возведены отклонения (х – А)к, моменты называются моментами 1-го, 2-го и т.д. порядков.
Расчет дисперсии методом условных моментов состоит в следующем:
Выбор условного нуля С;
Преобразование
фактических значений признака х
в упрощенные
х´
путем отсчета от условного нуля С
и уменьшения в d
раз:
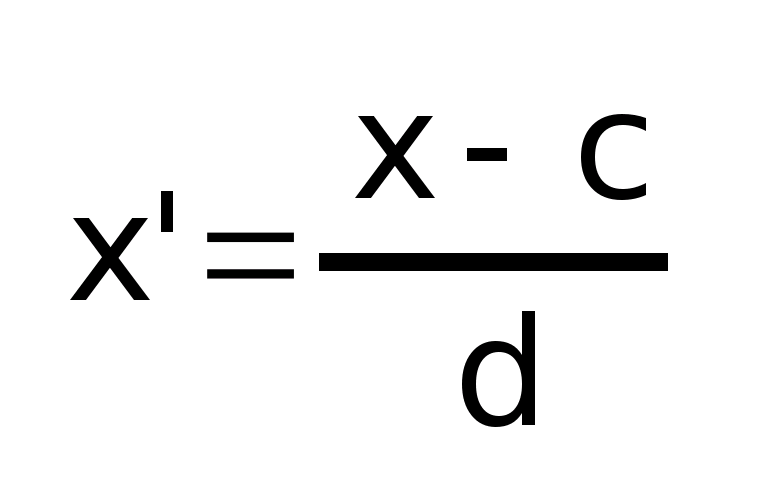
Расчет
1-го условного момента:
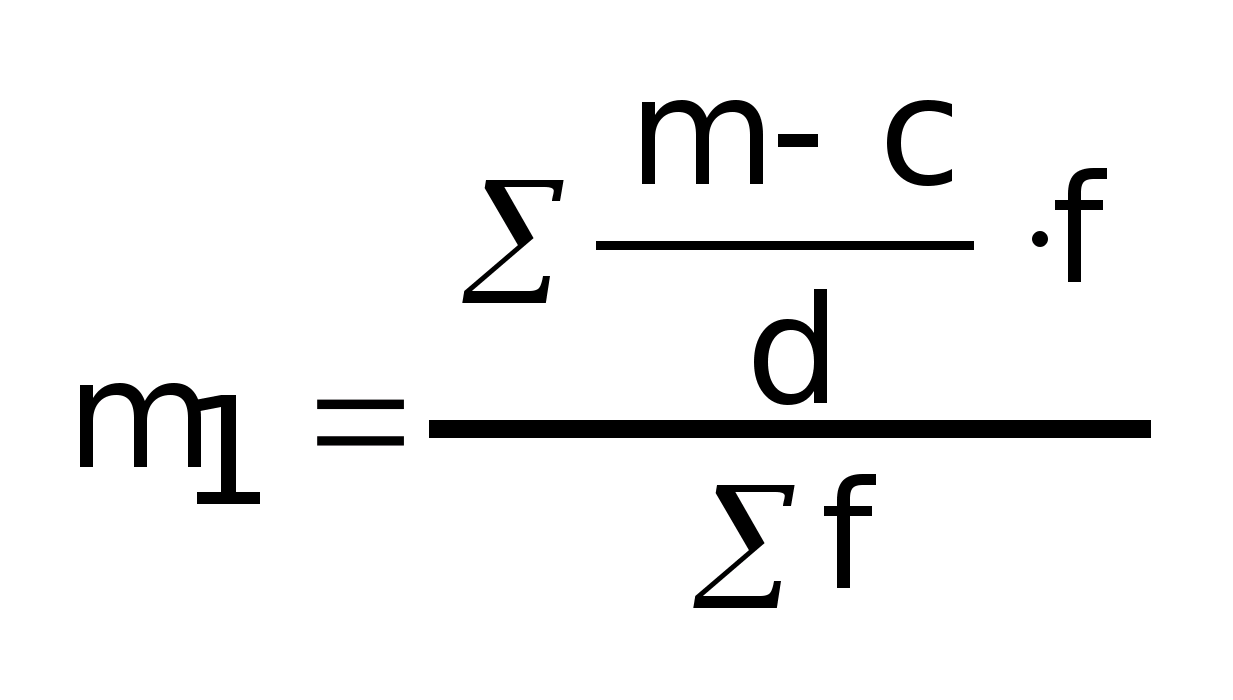
Расчет
2-го условного момента:
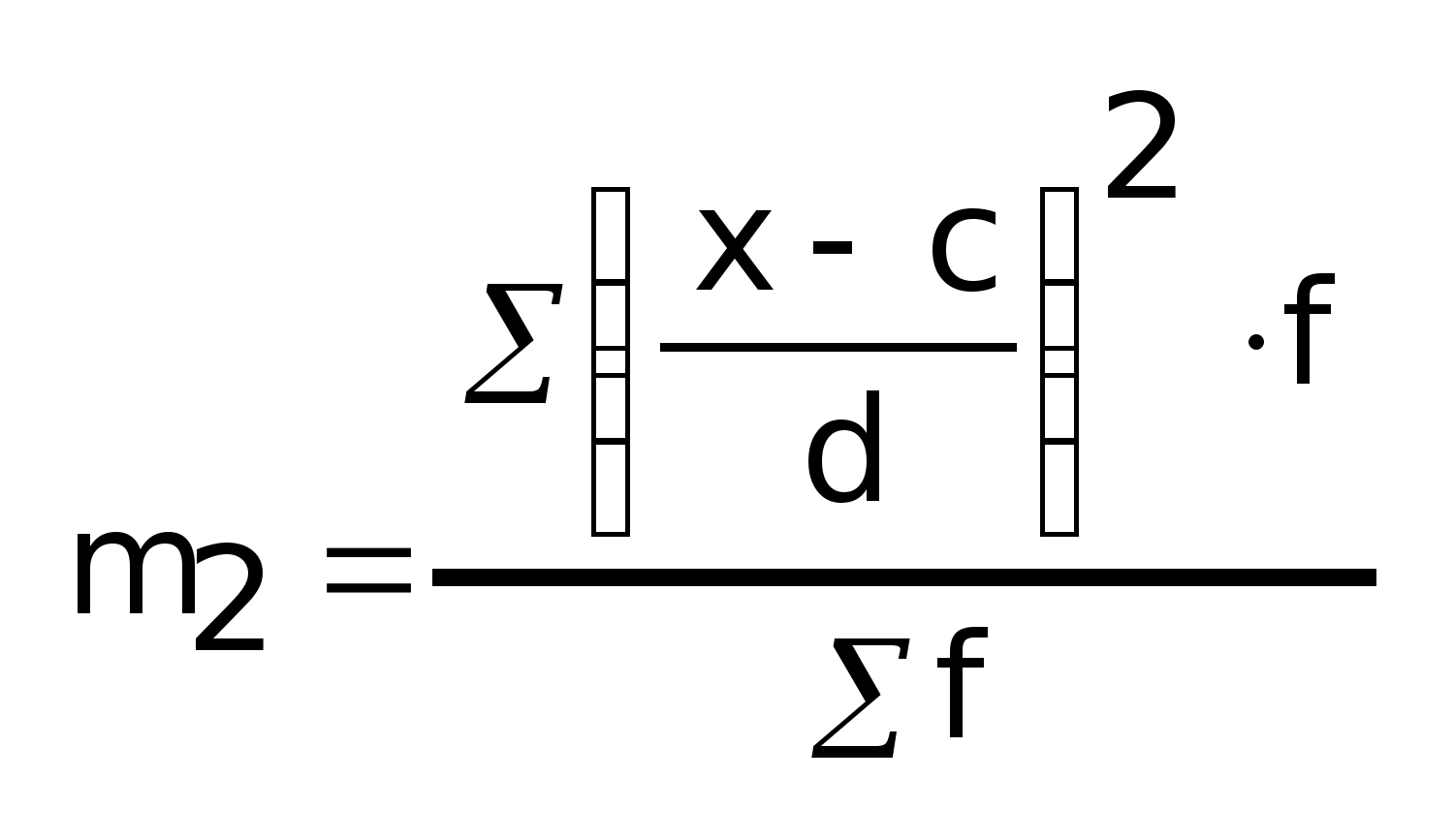
Расчет
1-го порядка начального момента:
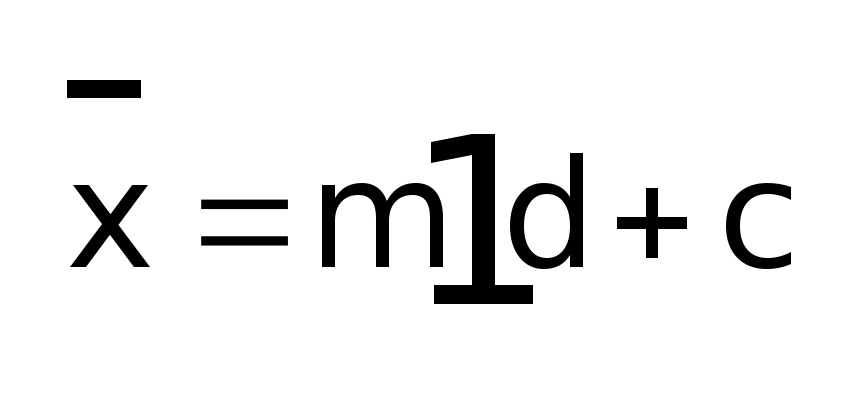
Дисперсии
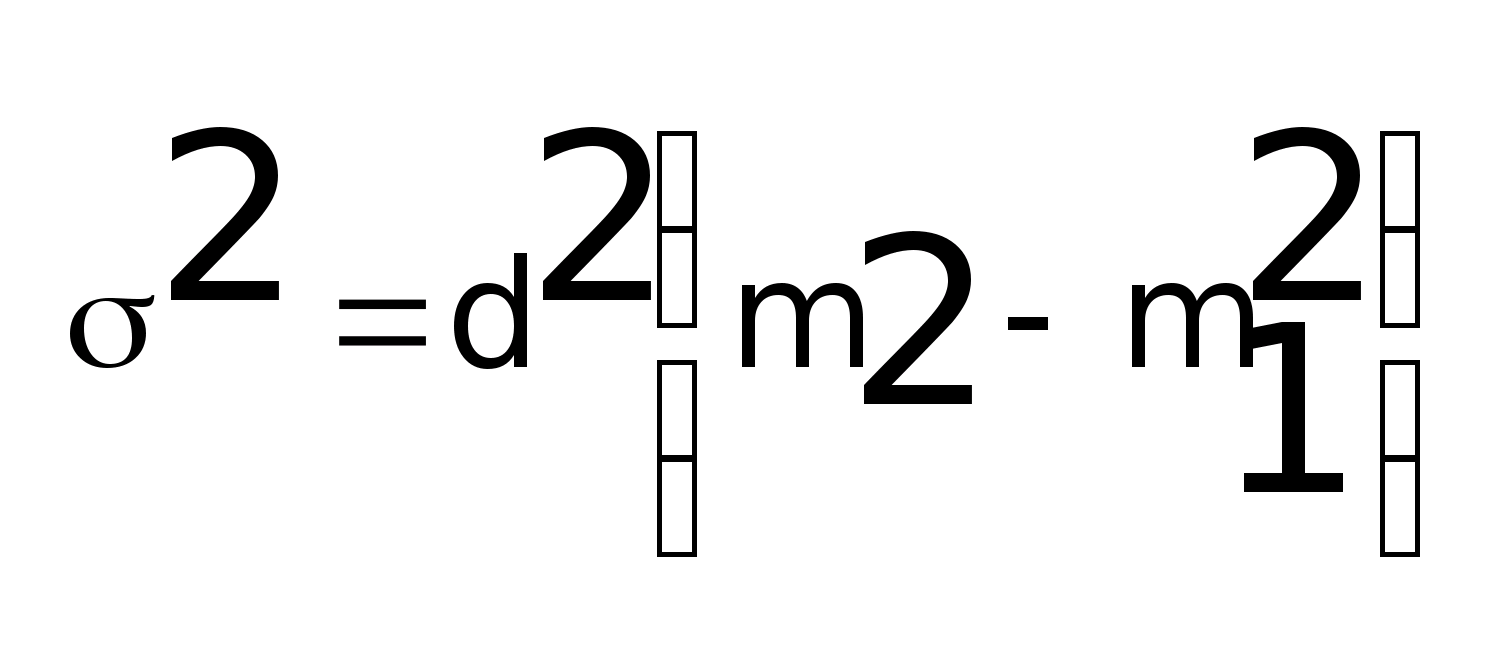
Среднее квадратичное отклонение рассчитывается по данным о дисперсии = 2
Относительные величины вариации
Коэффициент
осцилляции отражает относительную
колеблемость крайних значений признака
вокруг средней
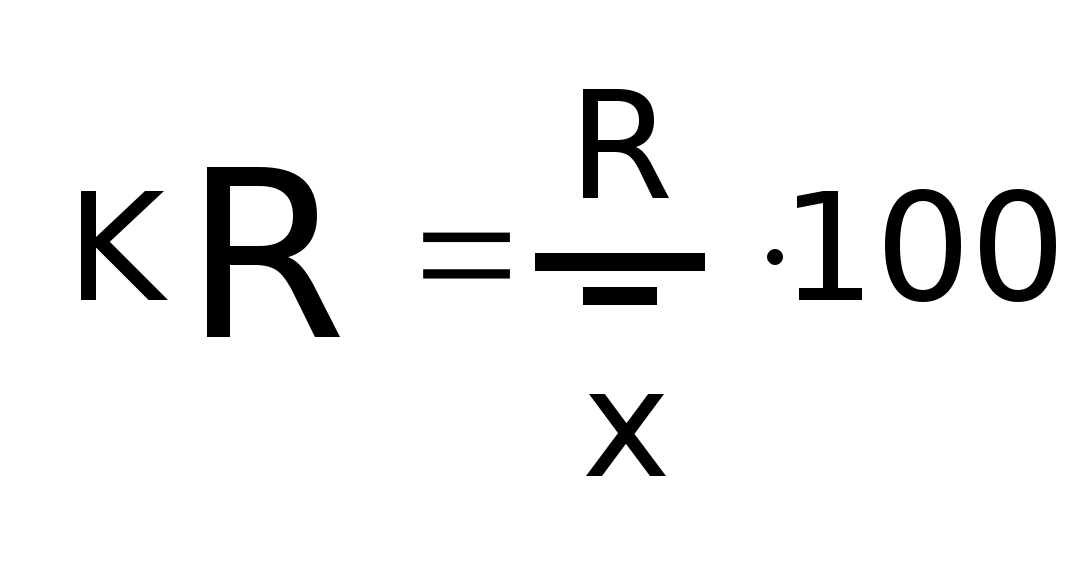
Относительное
линейное отклонение:
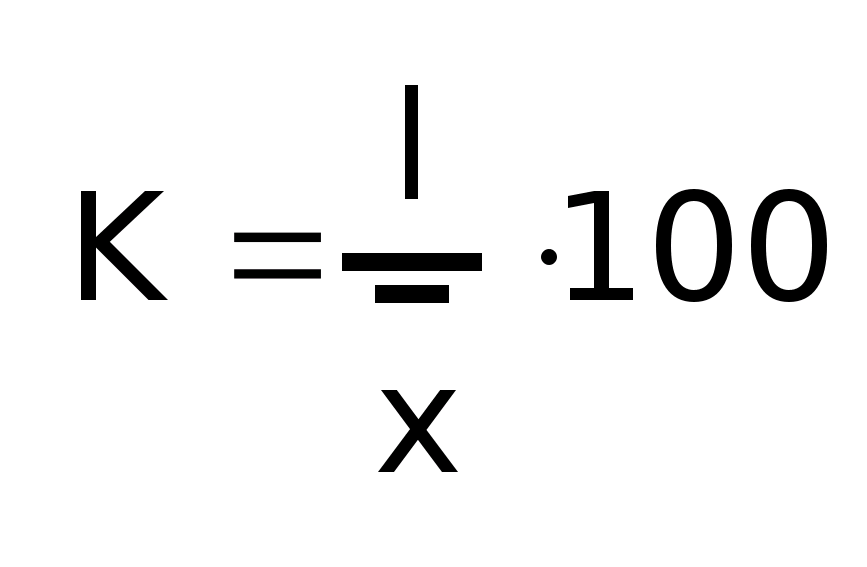
Коэффициент
вариации:
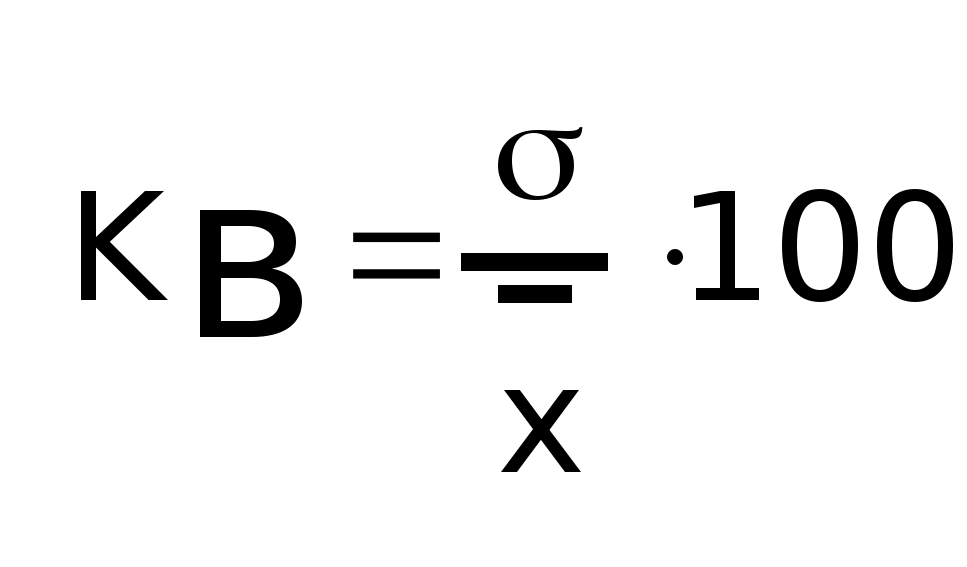
Коэффициент
асимметрии:
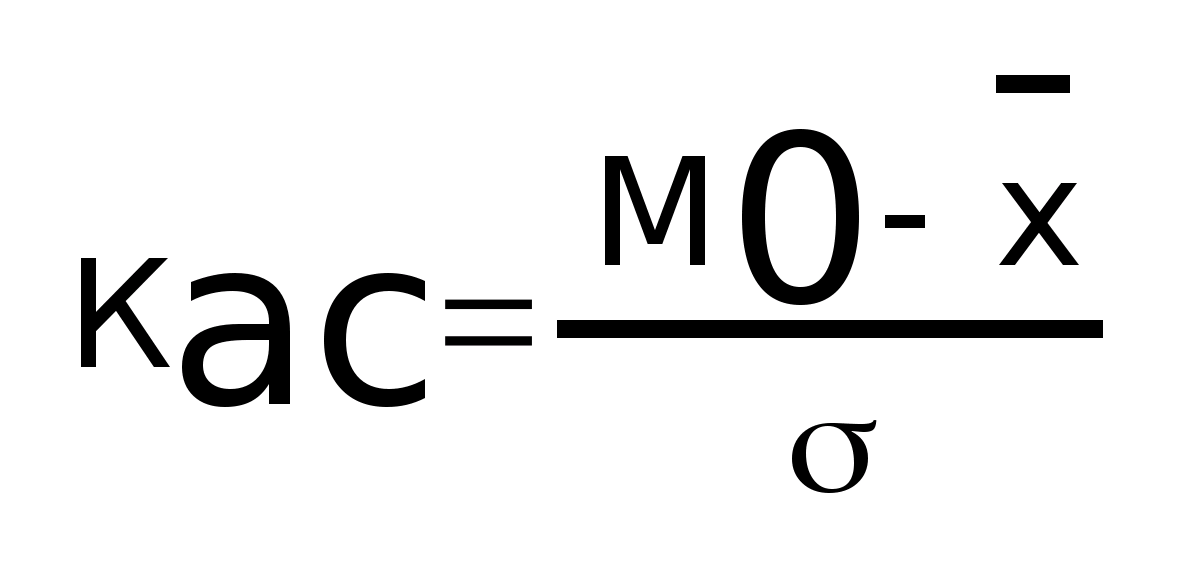
Виды дисперсий и правило сложения дисперсий
Общая
дисперсия:
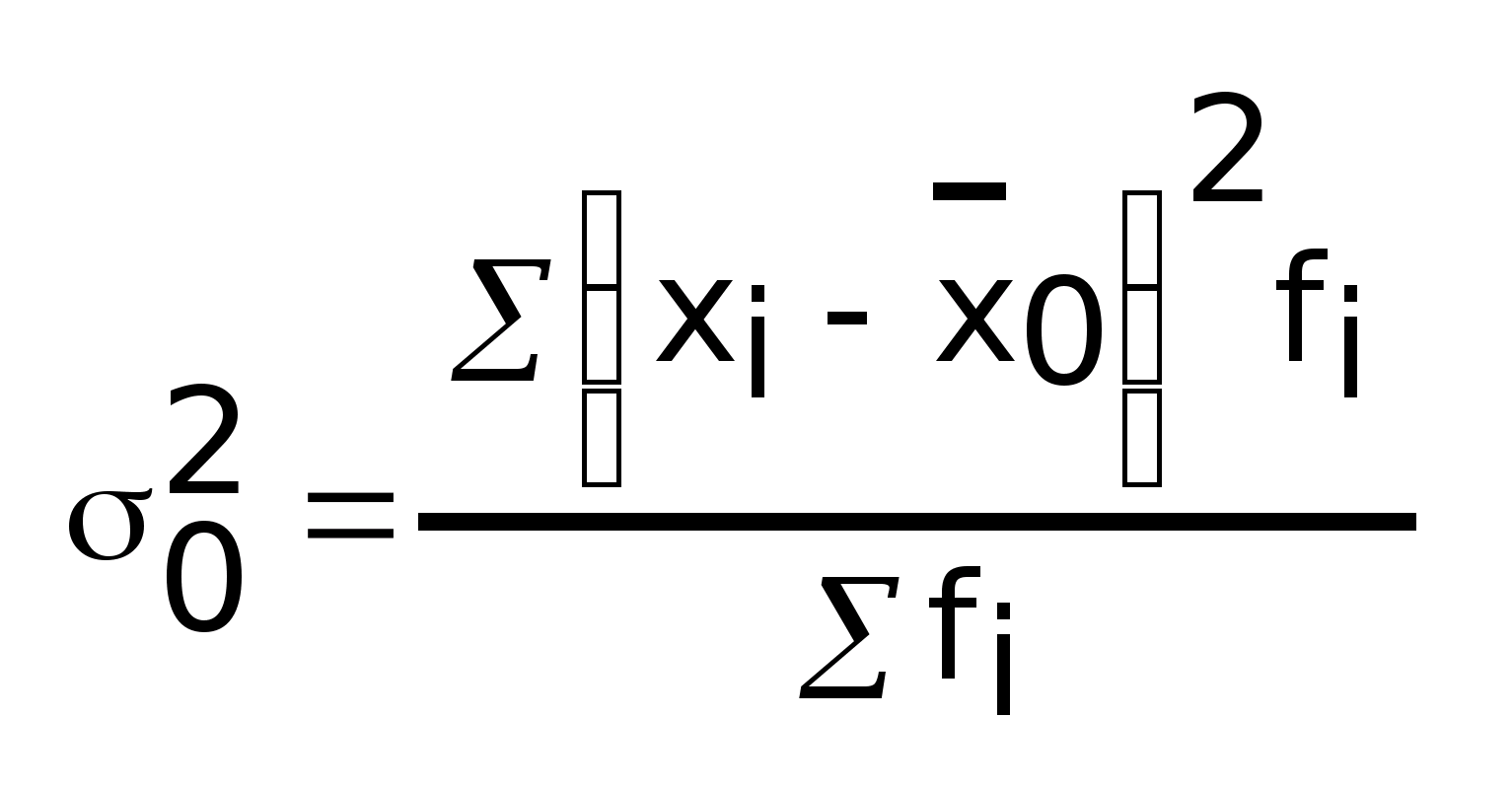
где 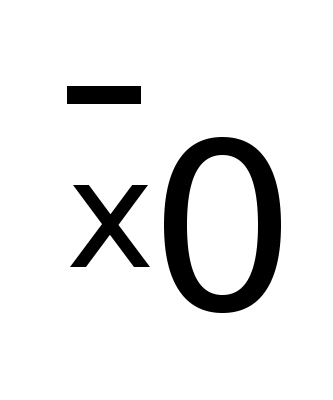 - общая
средняя всей совокупности
- общая
средняя всей совокупности
Межгрупповая
дисперсия:
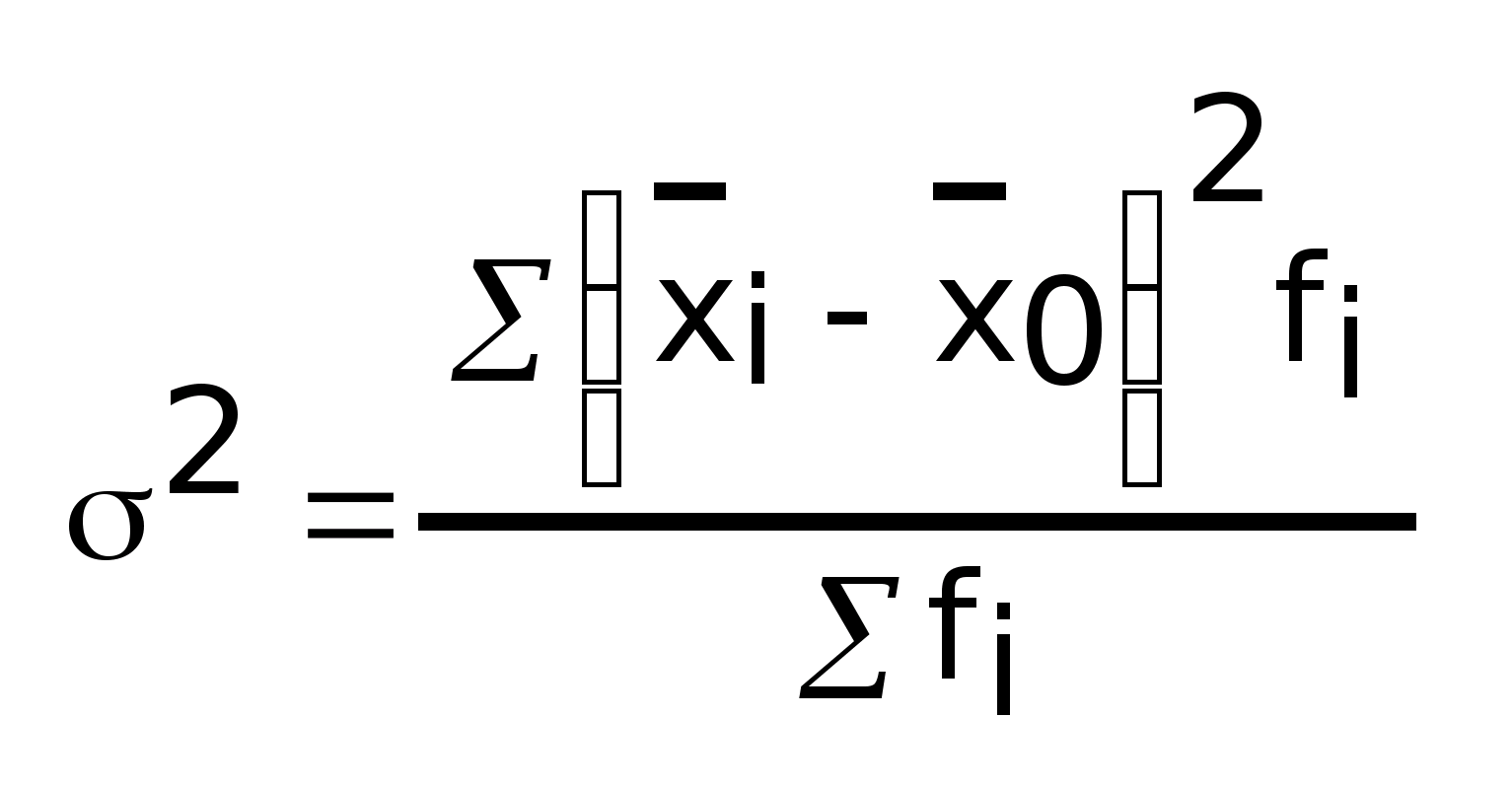
где
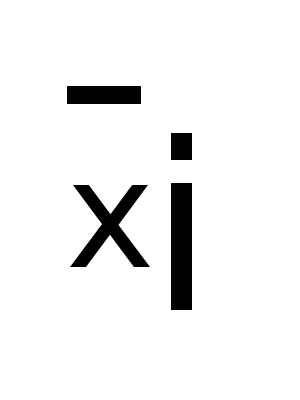 - средняя
по отдельным группам
- средняя
по отдельным группам
Средняя
внутри групповых дисперсий
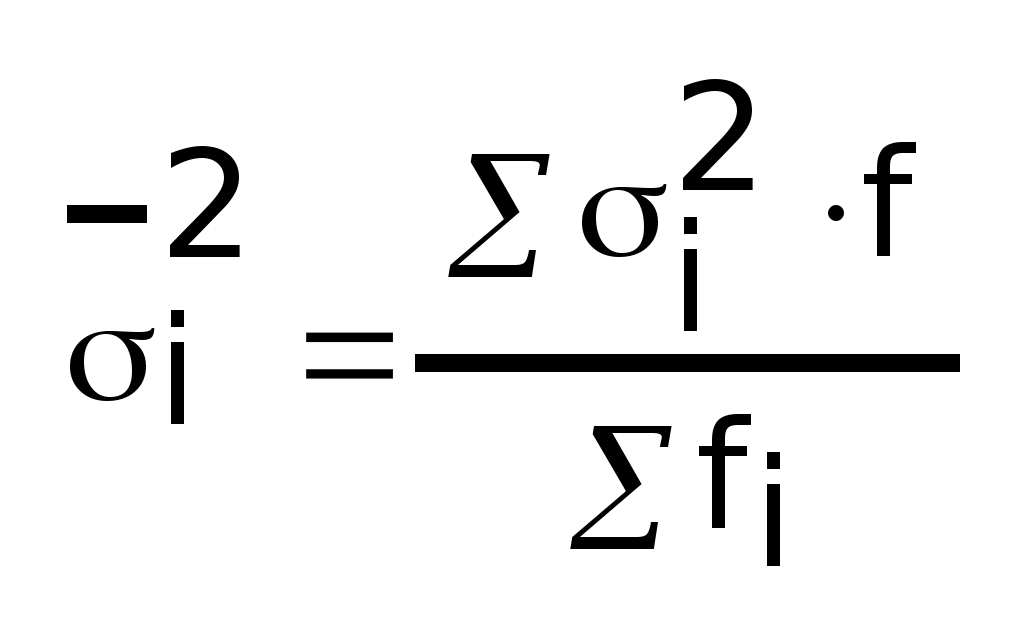
Общая
дисперсия равна сумме из межгрупповой
дисперсии и средней внутригрупповой
дисперсии:
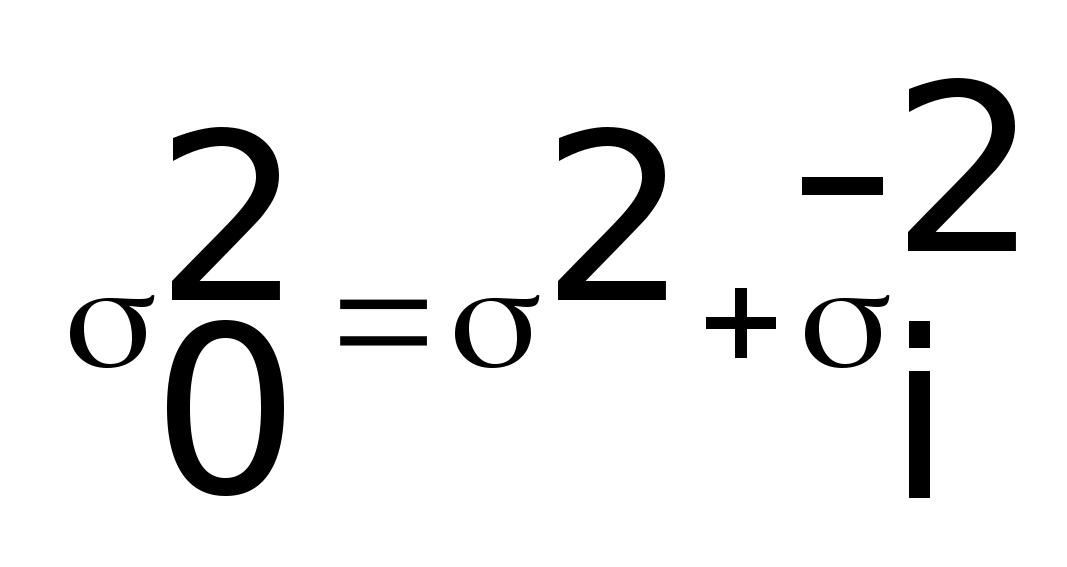
Дисперсия альтернативного признака.
Она равна произведению доли единиц, обладающих признаком и доли единиц, не обладающих им
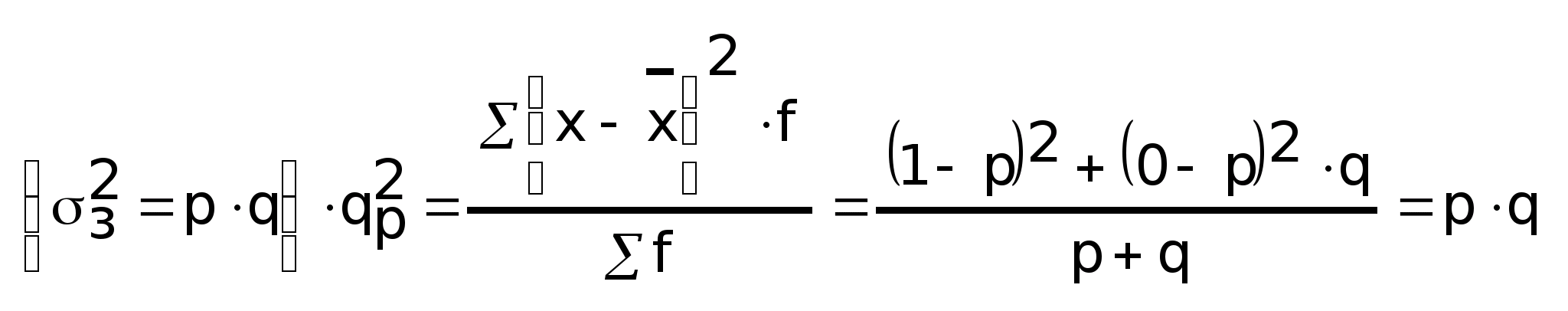
Тема 4. Ряды динамики
4.1. Понятие о рядах динамики, виды рядов динамики
Ряды динамики – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
Ряды динамики бывают:
В зависимости от времени – моментные и интервальные ряды.
От формы представления уровней – ряды абсолютных, относительных и средних величин.
От расстояния между датами – полные и неполные хронологические ряды.
От числа показателей – изолированные и комплексные ряды.
4.2.Производные показатели рядов динамики
|
Показатели |
Базисный |
Цепной |
|
Абсолютный прирост |
у>i> – у>0> |
у>i> – у>i-1> |
|
Коэффициент роста (К>р>) |
у>i> : у>0> |
у>i> : у>i-1> |
|
Темп роста (Т>р>) |
(у>i> : у>0>) · 100 |
(у>i> : у>i>>-1>) · 100 |
|
Коэффициент прироста (К>пр>) |
К>р> – 1; у>i> – у>0> у>0> Δ>баз> : у>0> |
К>р> – 1; у>i> – у>i>>-1> у>i>>-1> Δ>цеп> : у>i>>-1> |
|
4.3. Взаимосвязь цепных и базисных темпов роста |
||
|
Темп прироста (Т>пр>) |
К>пр> · 100 : Т>р> - 100 |
К>пр> · 100 : Т>р> - 100 |
|
Абсолютное значение 1-го процентного прироста (1%А) |
у>0> : 100 |
у>i>>-1> : 100; Δ : Т>пр> у>i> - у>i>>-1> Т>р> - 100 |
Соотношения: у>2>/у>1> · у>3>/у>2> · у>4>/у>3> · у>5>/у>4> = у>5>/у>1> у>4>/у>1> : у>3>/у>1> = у>4>/у>3>
4.4. Средние показатели ряда динамики
Если
ряд динамики интервальный и содержит
все последовательные уровни, то средний
уровень определяется как средняя
арифметическая величина:
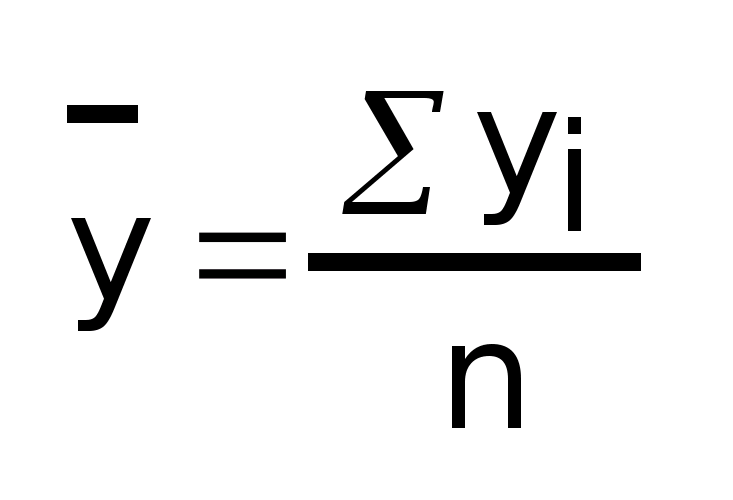 Если
ряд динамики моментный с одинаковыми
промежутками времени между датами, то
средняя хронологическая определяется
как простая арифметическая:
Если
ряд динамики моментный с одинаковыми
промежутками времени между датами, то
средняя хронологическая определяется
как простая арифметическая:
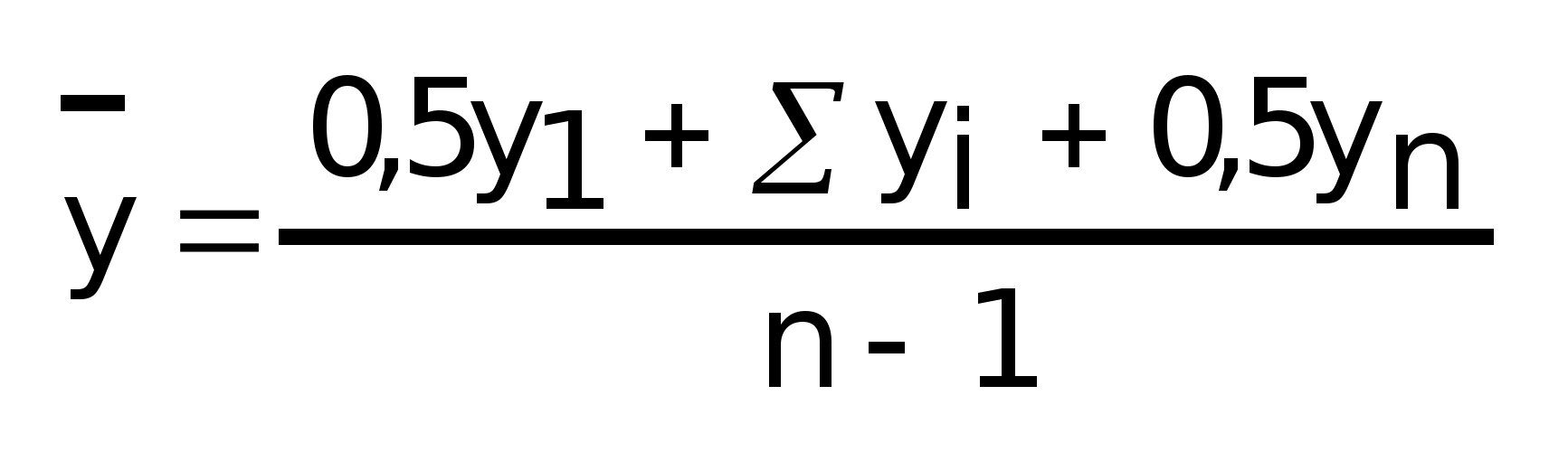
А
если с разновеликими интервалами между
датами, то как средняя арифметическая
взвешенная по времени:
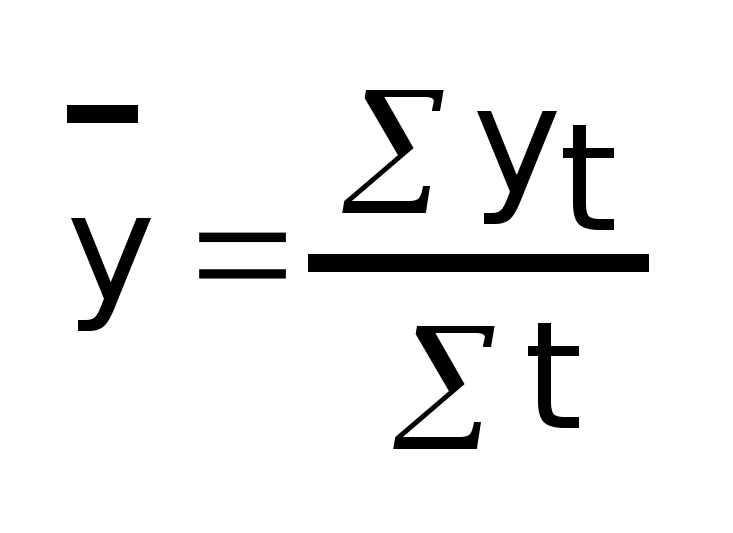 где t
- время, в течение которого уровень не
менялся Средний абсолютный прирост:
где t
- время, в течение которого уровень не
менялся Средний абсолютный прирост:
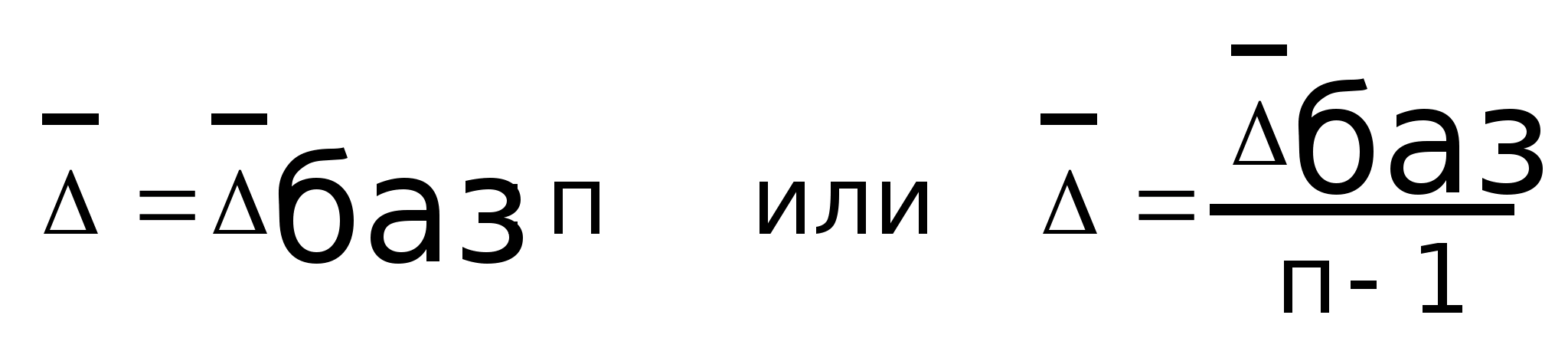 Средний
темп роста:
Средний
темп роста:
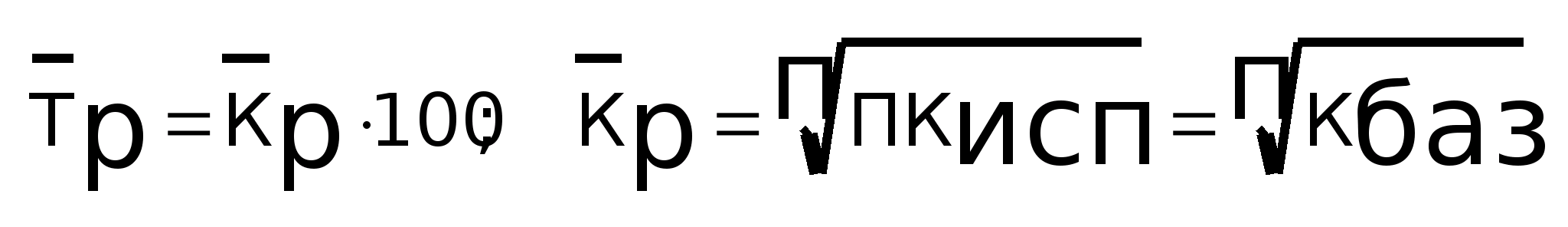
Средний
темп прироста:
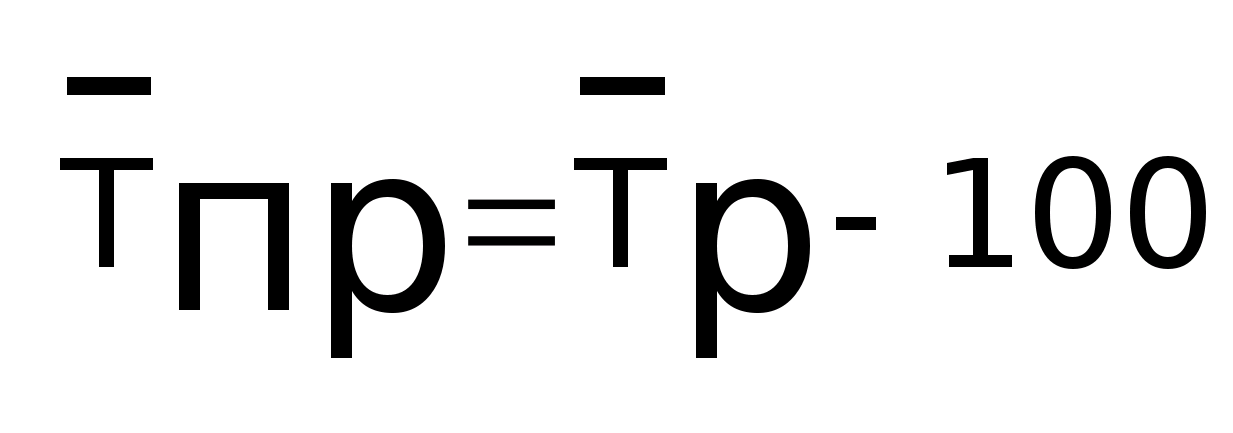
4.5. Измерение сезонности явлений.
Индексы сезонности. Построение сезонной волны
Метод простых средних:
а)
определяется средняя хронологическая
для каждого месяца
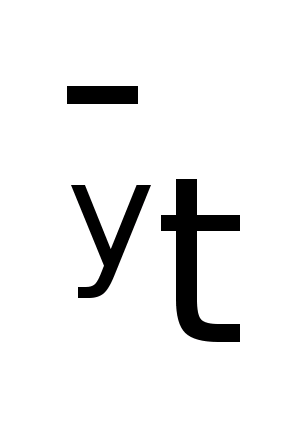 б)
средняя хронологическая общая:
б)
средняя хронологическая общая:
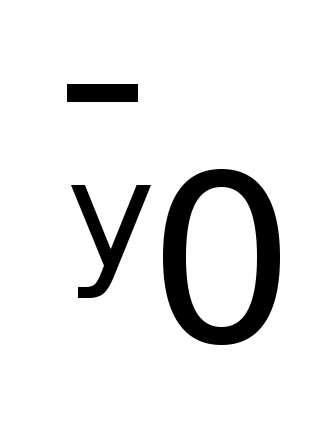 Индекс
сезонности:
Индекс
сезонности:
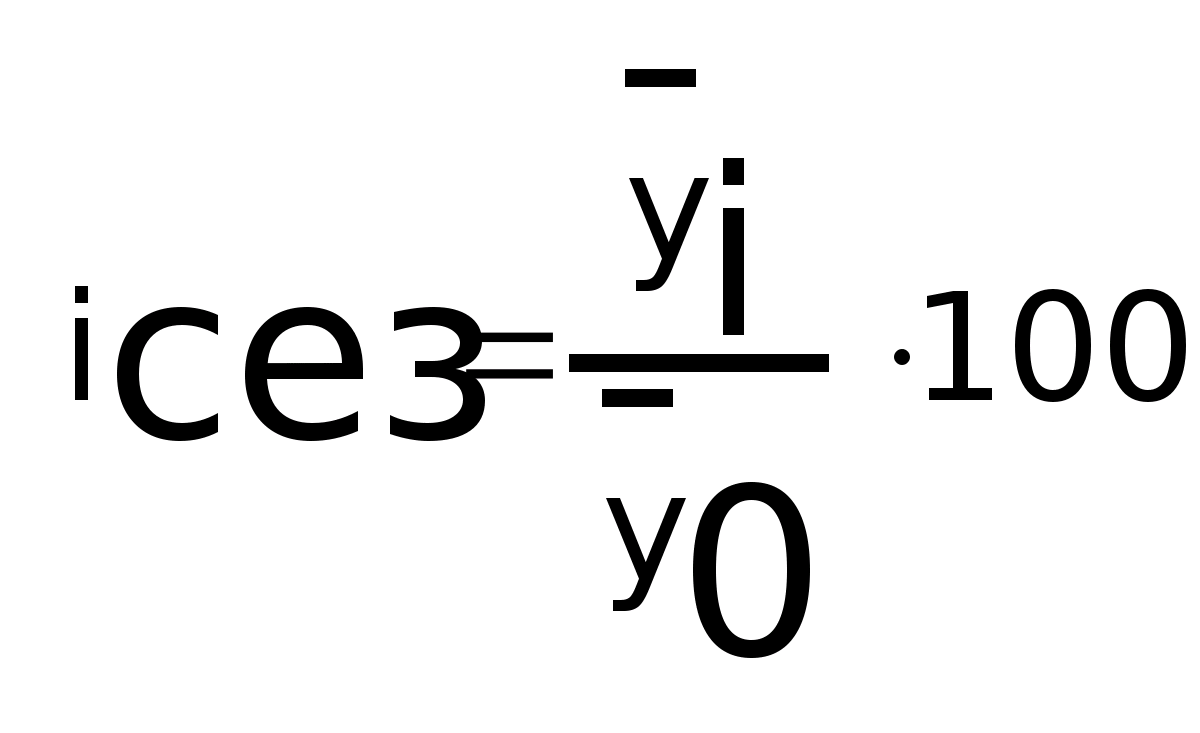
Метод
сравнения фактического и сглаженного
уровней а) метод скользящего среднего
уровня:
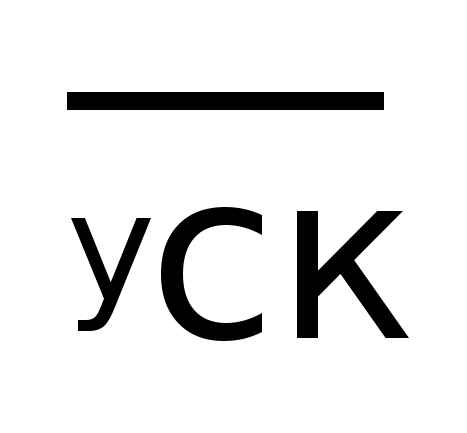
б)
метод аналитического выравнивания:
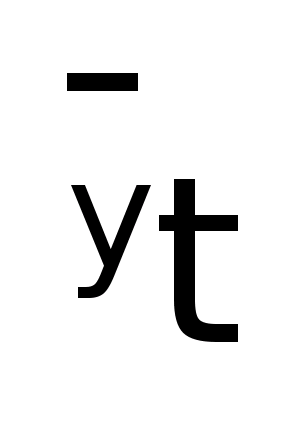
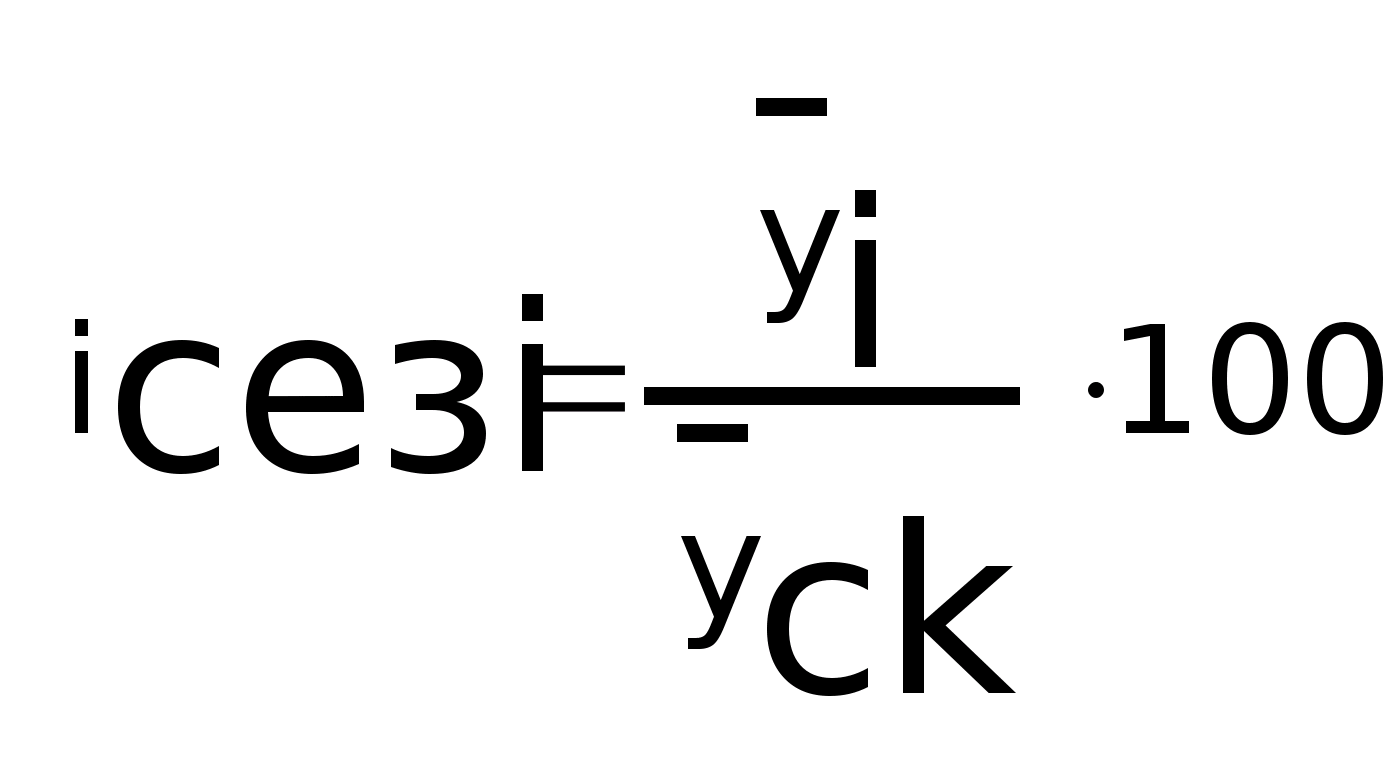
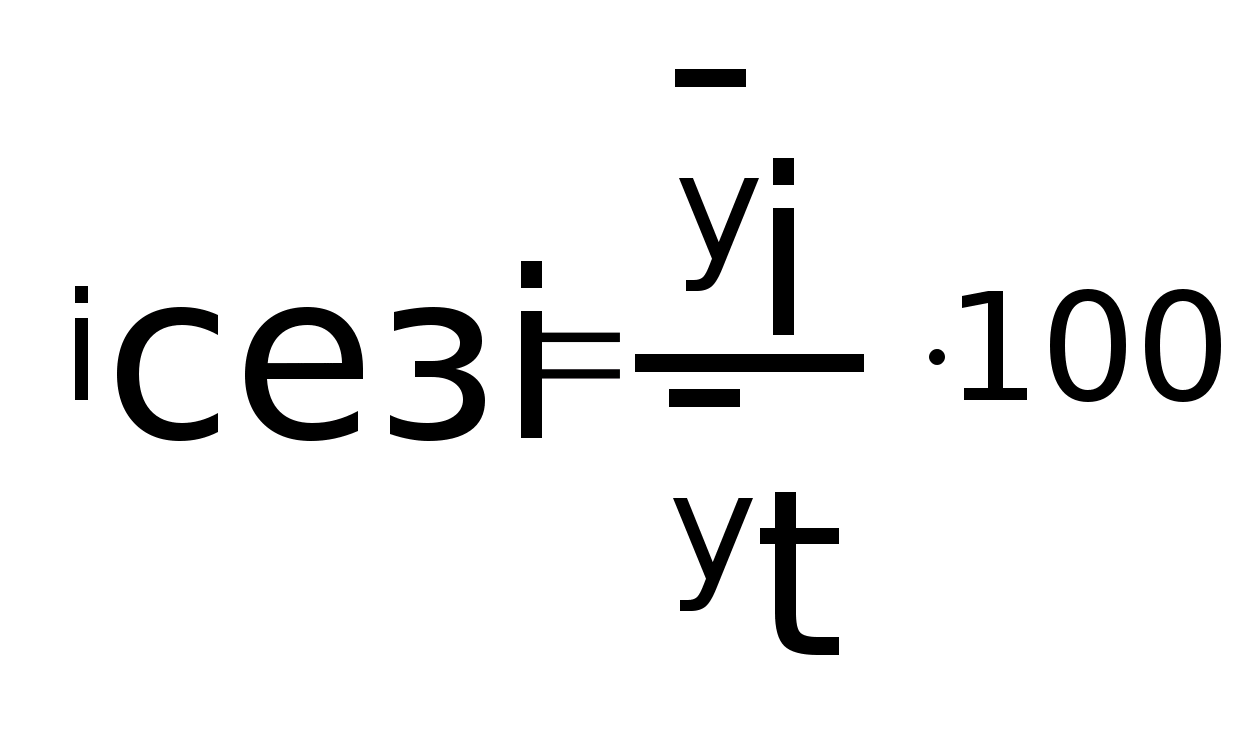
Колеблемость
уровня ряда измеряется средним отклонением
индекса сезонности i>сез>
от 100%:
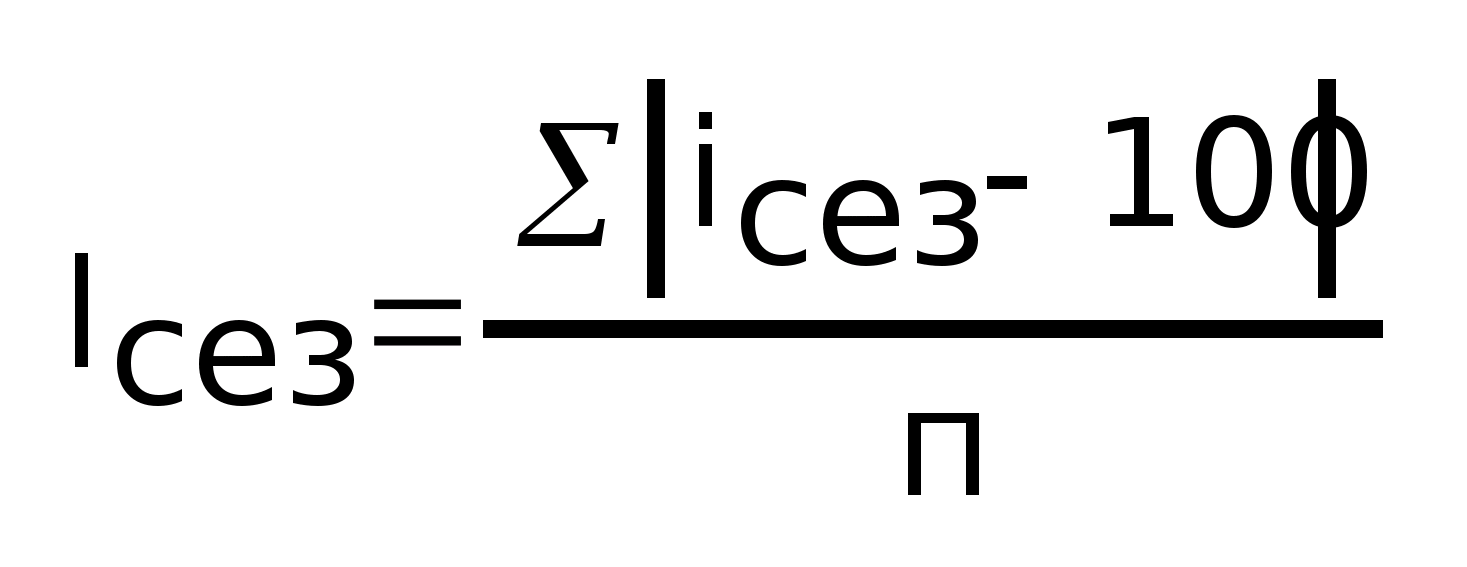 Среднее
квадратичное отклонение
Среднее
квадратичное отклонение
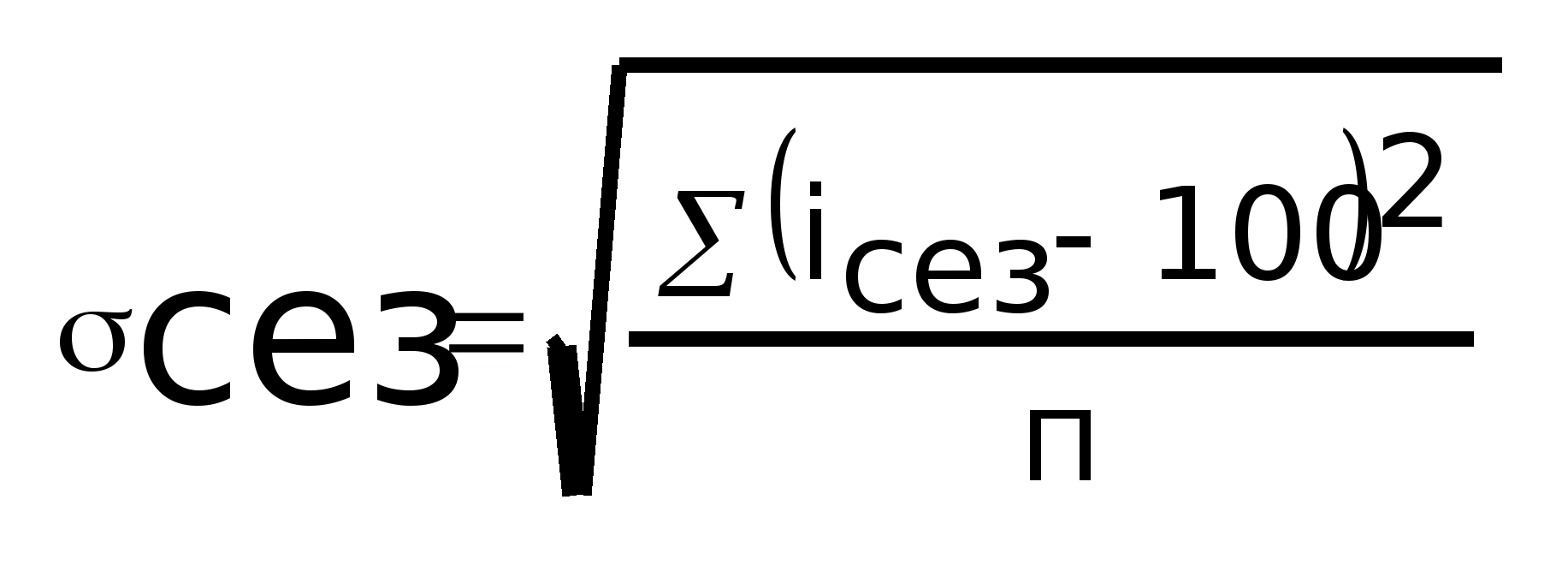
4.6. Выравнивание рядов динамики
Выравнивание рядов динамики производят одним из способов:
а) Механическое выравнивание состоит в укрупнении интервала времени и расчете средней хронологической
б)
Аналитическое выравнивание – это
описание тенденций с помощью подбора
адекватной модели, представляющей
математическую функцию зависимости
среднего уровня от времени:
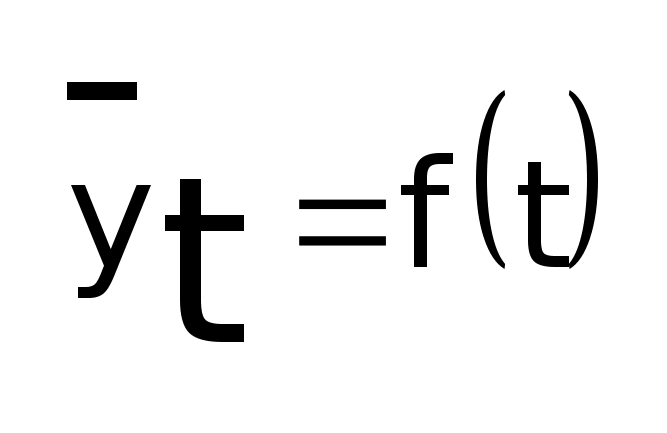 По
уравнению прямой:
По
уравнению прямой:
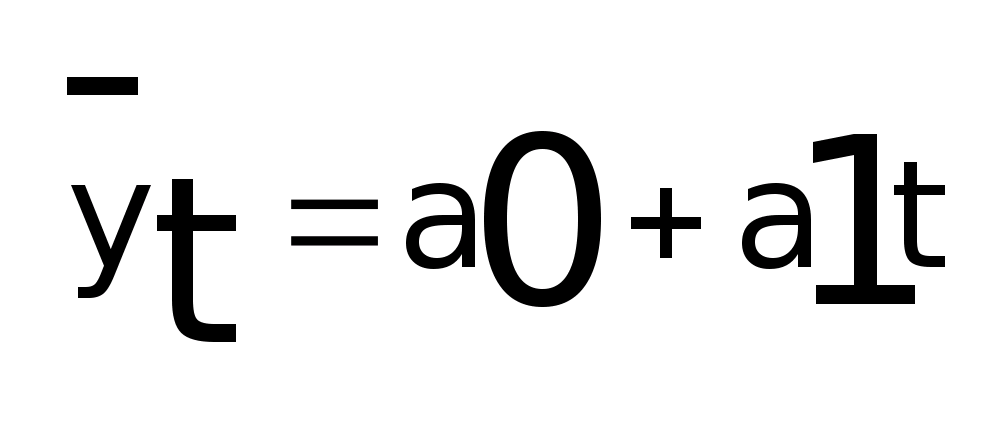
где a>0 > и а>1> - это параметры уравнения, которые рассчитываются на
основе
фактических данных методом наименьших
квадратов
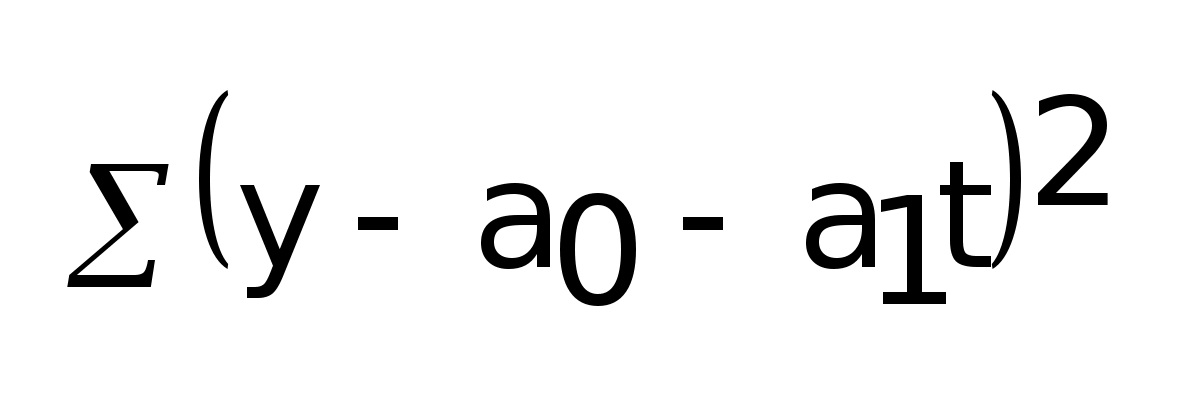
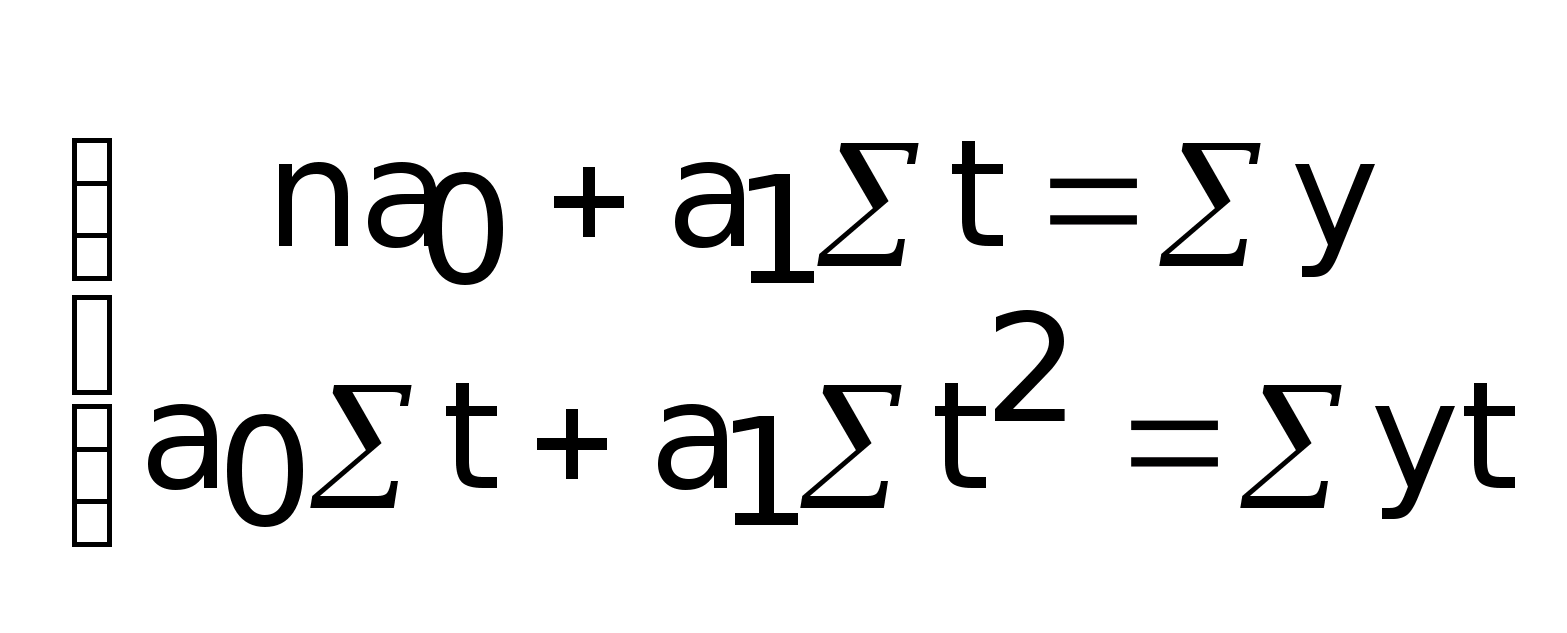 - это условное
время принятое от какой-то базы.
- это условное
время принятое от какой-то базы.
Выравнивание
может выполняться по параболе 2-го
порядка:
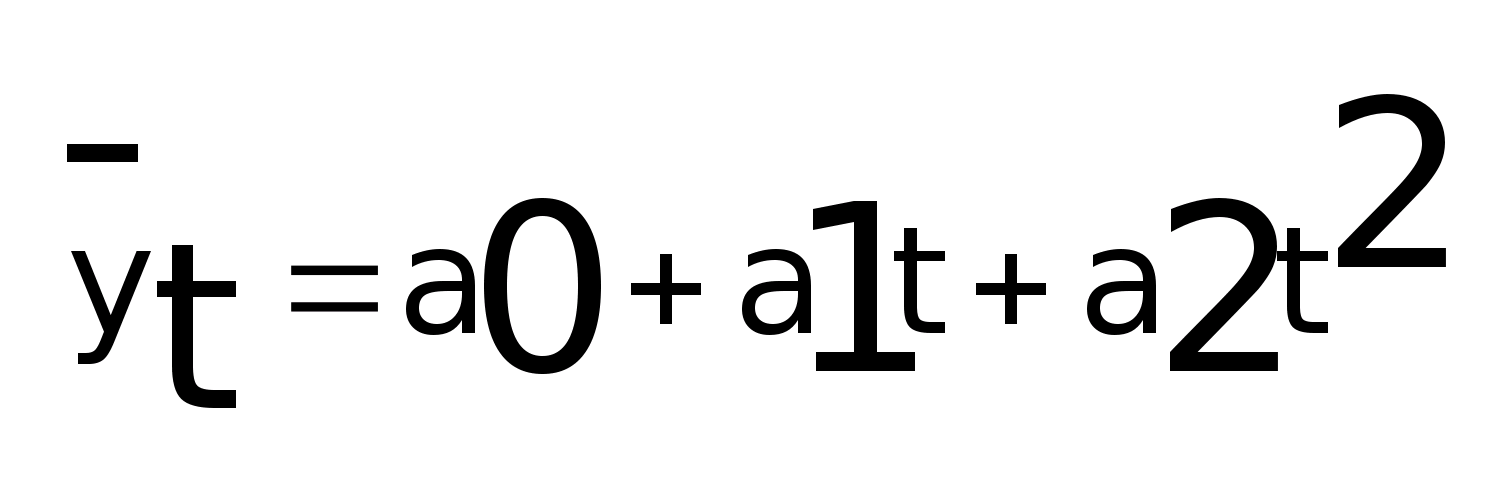 а>0>,
а>1,>
а>2> -параметры,
определяемые с помощью системы
уравнений:
а>0>,
а>1,>
а>2> -параметры,
определяемые с помощью системы
уравнений:
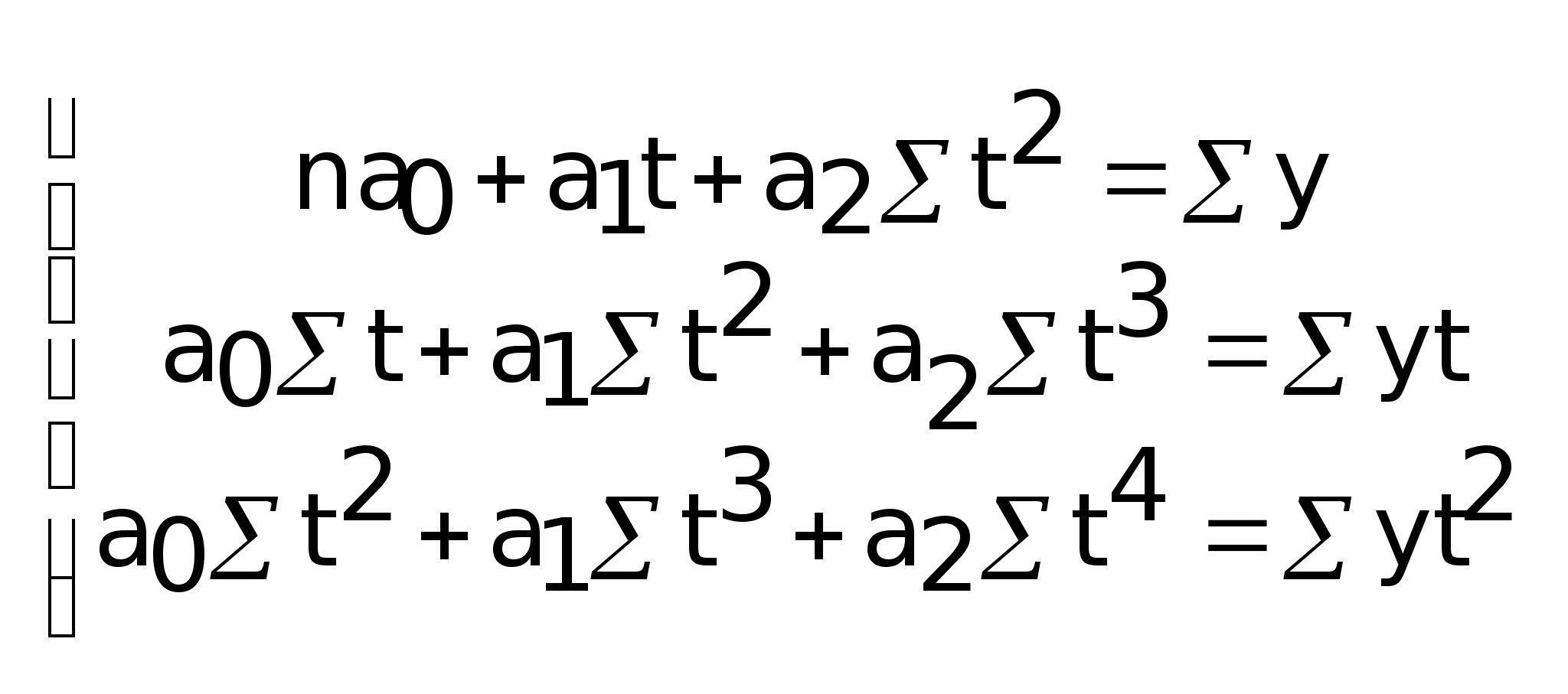 если
Σt
= 0, то Σt3
= 0
если
Σt
= 0, то Σt3
= 0
Если
применяется показательная функция, то
уравнения взаимосвязи следующая:
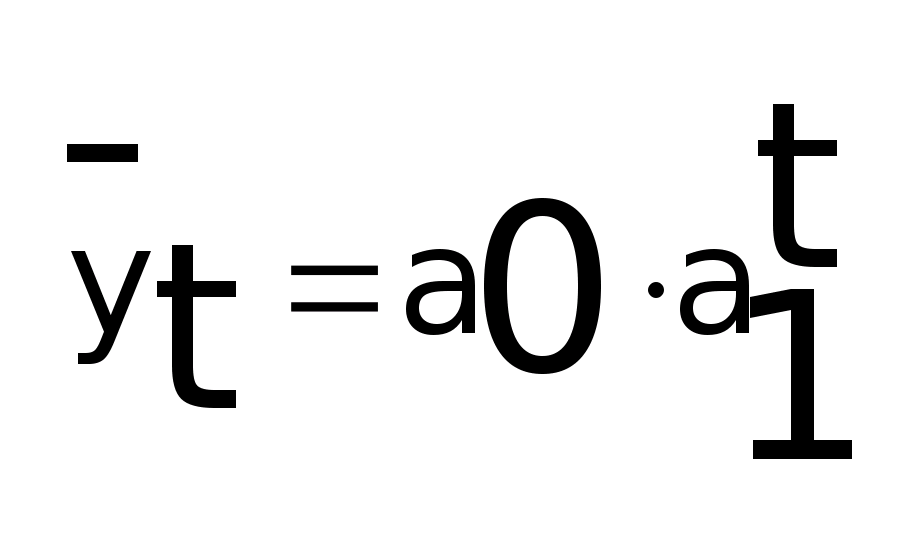 , для решения такой модели переходят к
логарифмам:
, для решения такой модели переходят к
логарифмам:
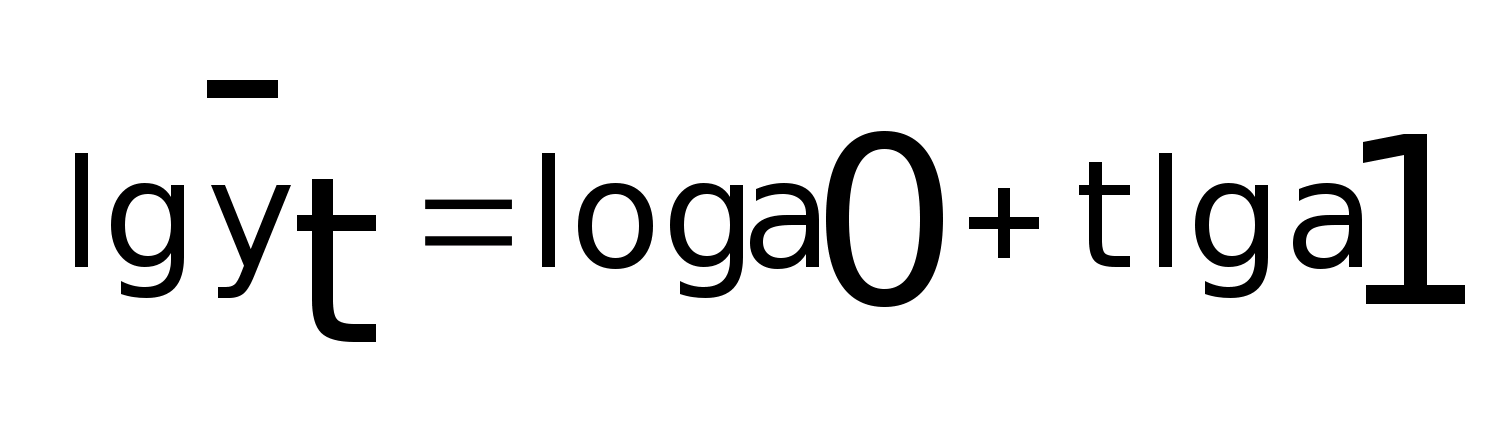
Это уравнения прямой для логарифмов уравнений, поэтому выравнивание осуществляется аналогично прямой, но предварительно определяются логарифмы
При выборе модели можно руководствоваться правилами
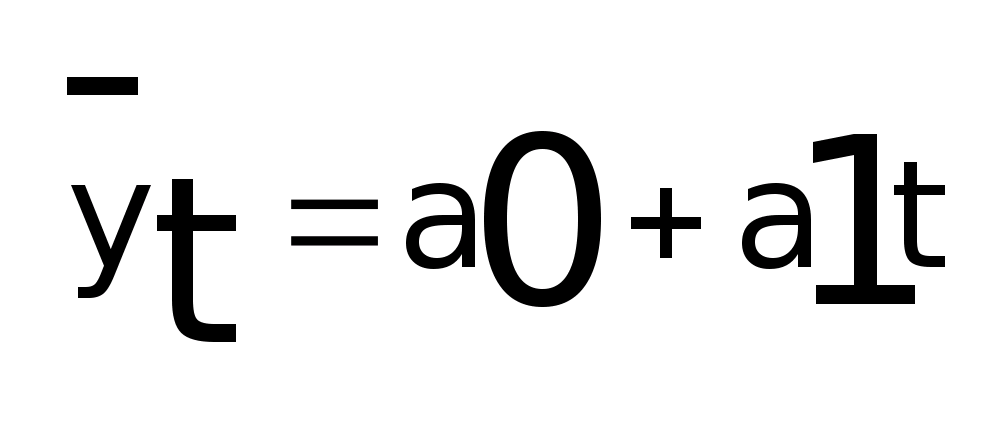 ,
если абсолютные приросты колеблются
около постоянной величины, то можно
использовать модель прямой линии
,
если абсолютные приросты колеблются
около постоянной величины, то можно
использовать модель прямой линии
Δy = у>i> - у>i-1>; а>0> - база; а>1>t - прирост.
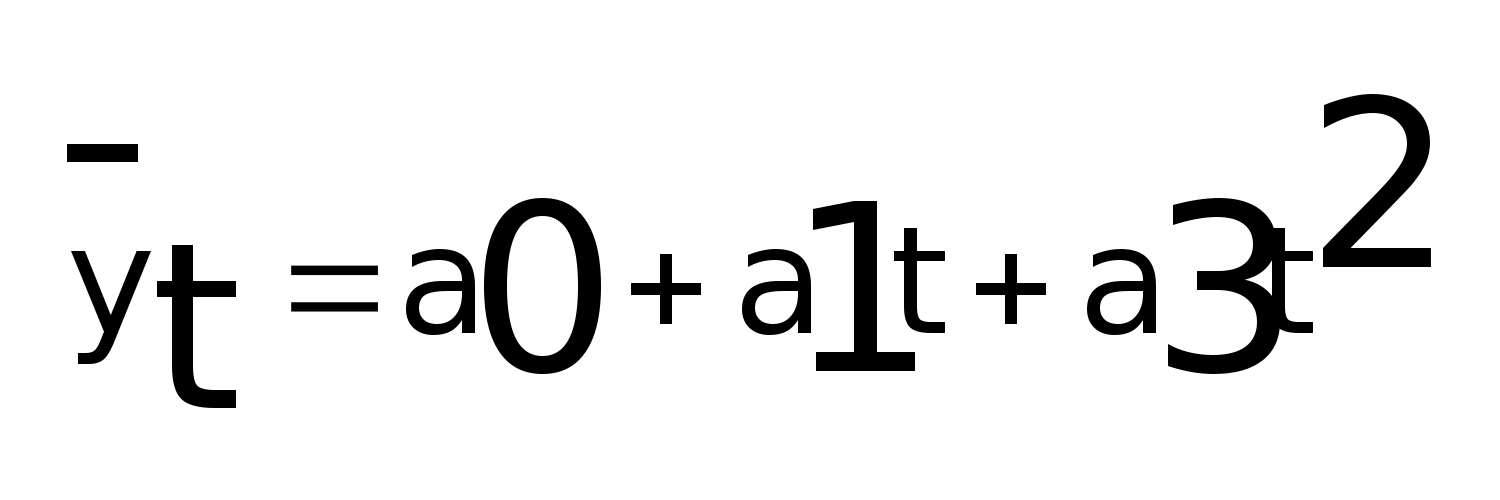 ,
если приросты приростов, т.е. ускорение
колеблется около постоянной величины,
то можно использовать параболу 2-го
порядка: а>0 >-
база; а>1>t -
прирост; а>2>t2 -
ускорение
(Δу>2>
– Δу>1>)
,
если приросты приростов, т.е. ускорение
колеблется около постоянной величины,
то можно использовать параболу 2-го
порядка: а>0 >-
база; а>1>t -
прирост; а>2>t2 -
ускорение
(Δу>2>
– Δу>1>)
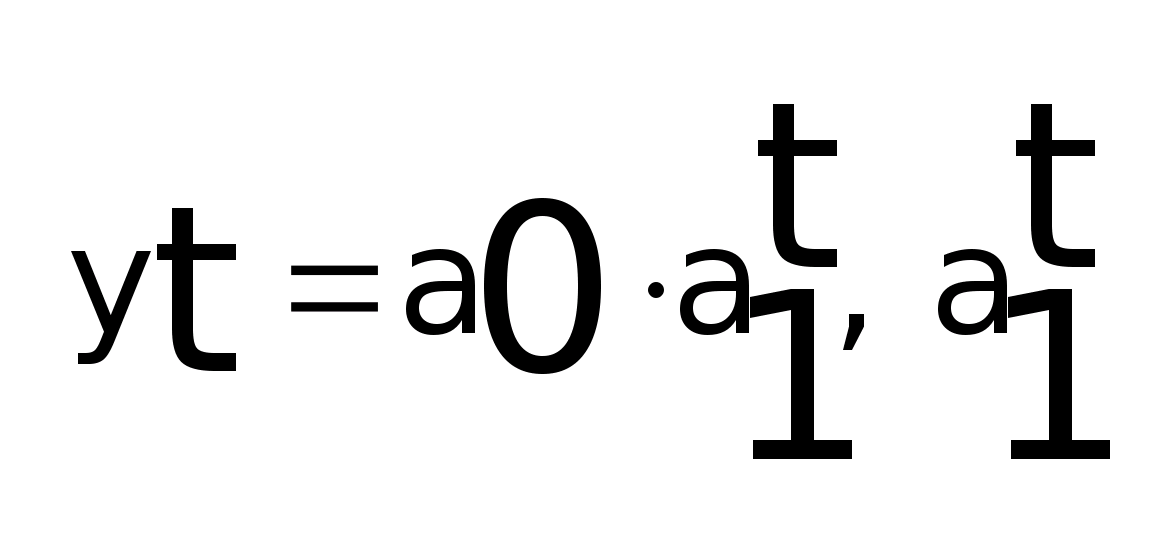 -
ср. коэффициент роста, если ежегодные
темпы роста примерно постоянны, то
можно использовать модель показательной
функции.
-
ср. коэффициент роста, если ежегодные
темпы роста примерно постоянны, то
можно использовать модель показательной
функции.
6. Индексы
6.1. Понятие индекса, индивидуальные и общие индексы, различие между ними
Индекс – это относительная величина сравнения сложных совокупностей и отдельных их единиц, которая показывает изменение изучаемого явления:
Бывают индексы общими и индивидуальными.
1. Общий индекс цен в агрегатной форме:
а)
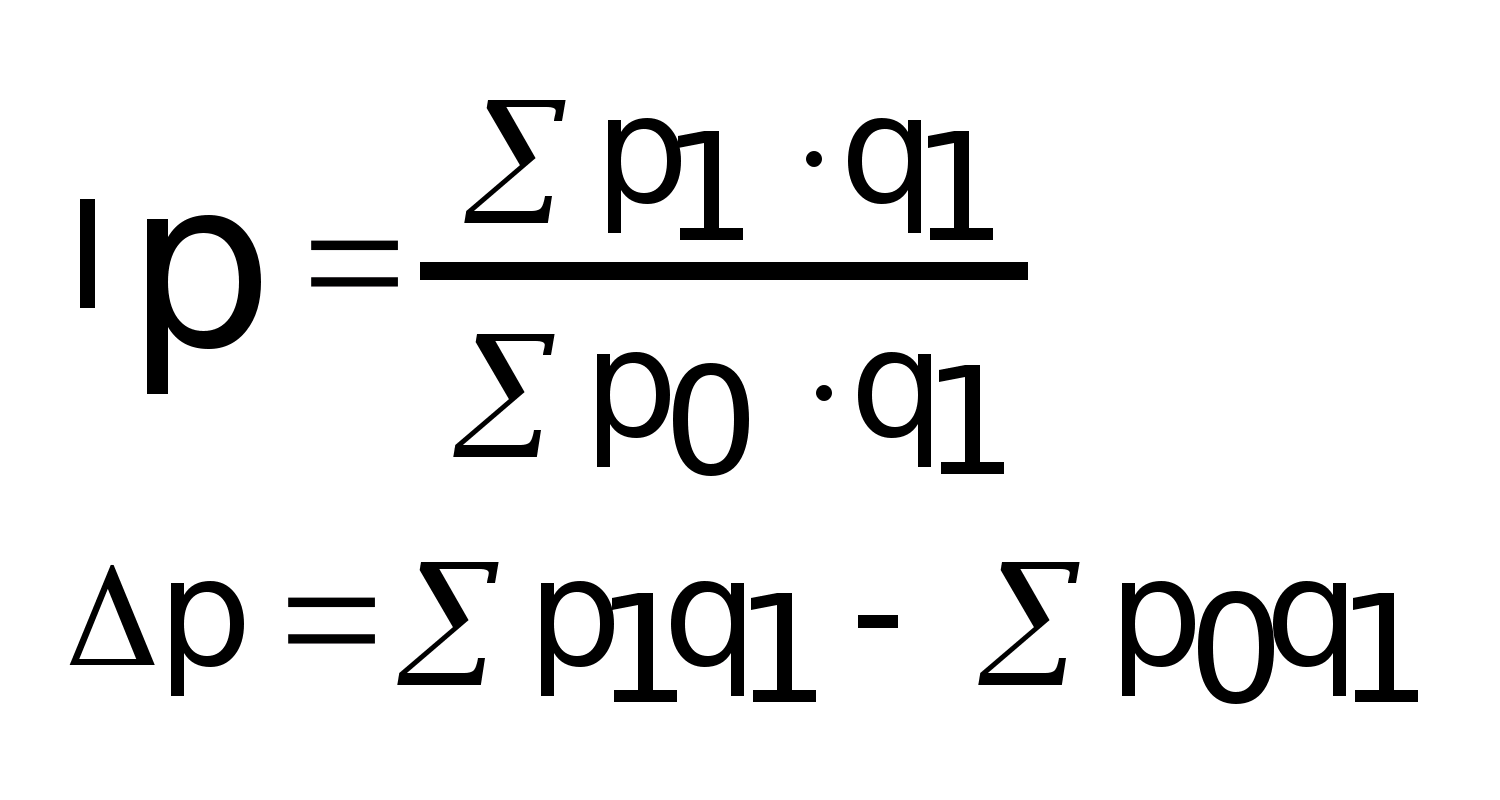 -
индекс Пааше б)
-
индекс Пааше б)
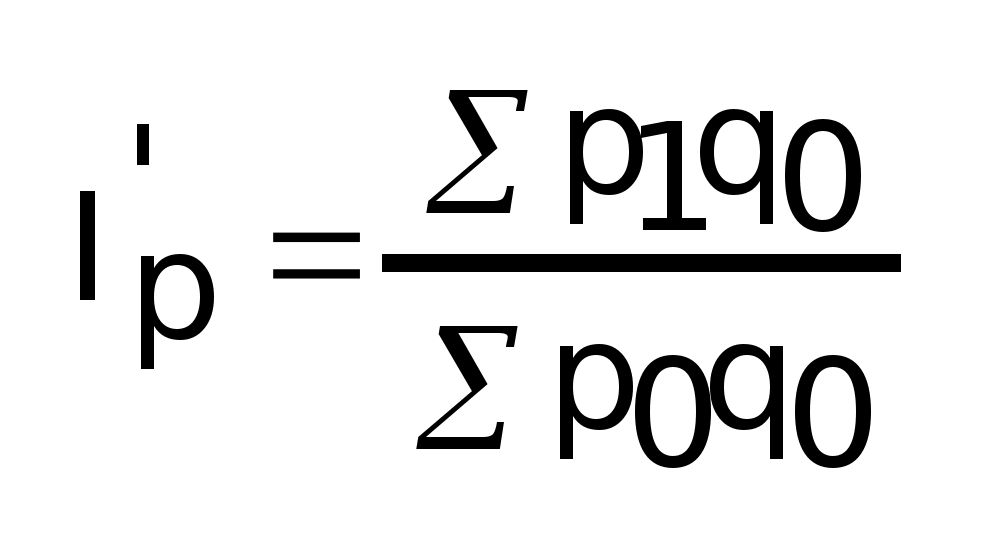 - индекс Ласпейреса
- индекс Ласпейреса
Агрегатный
индекс физического объема
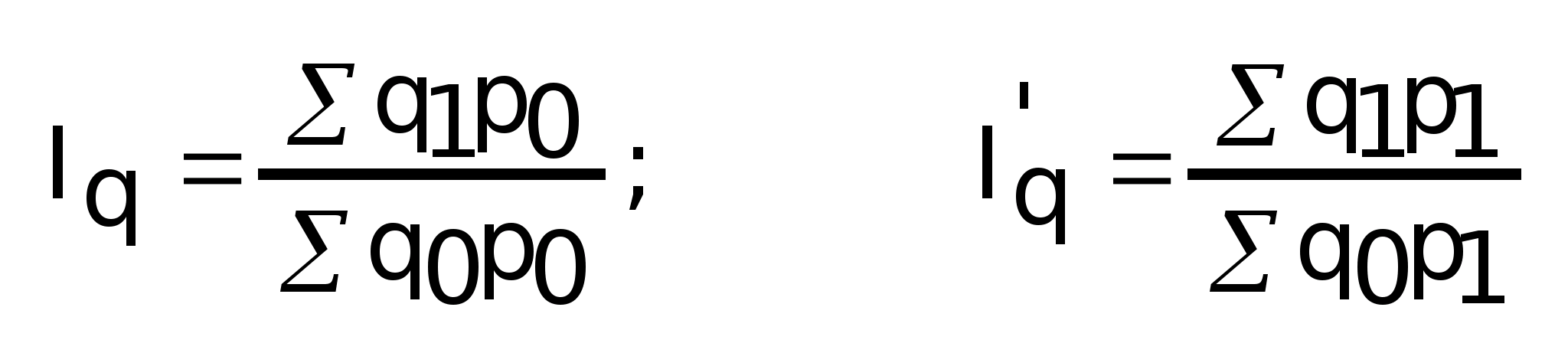
Общий
индекс
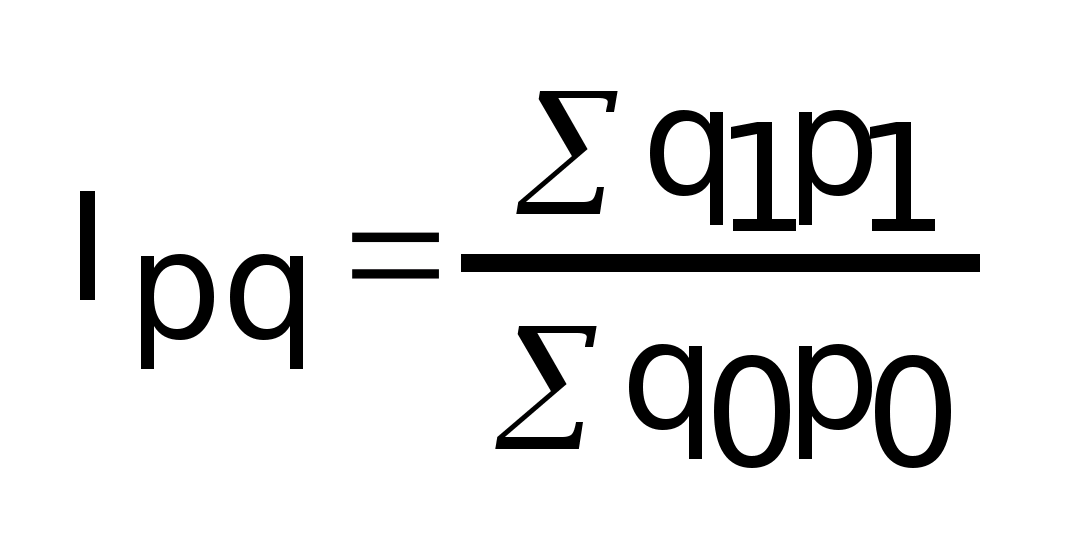
2. Индексы как средние величины:
Индекс
физического объема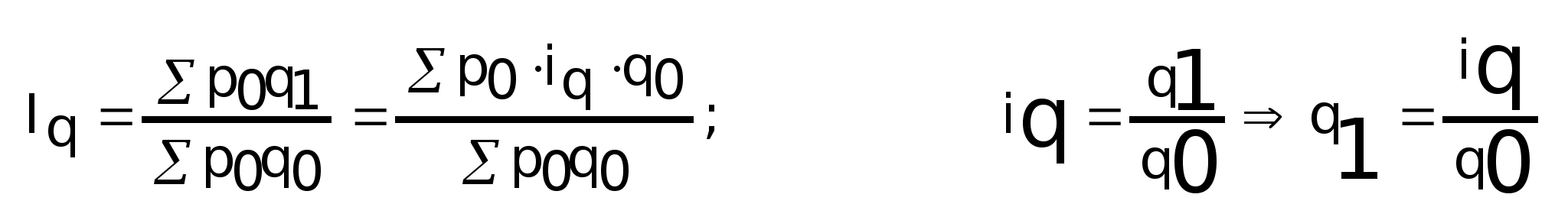
Индекс
цен Пааше
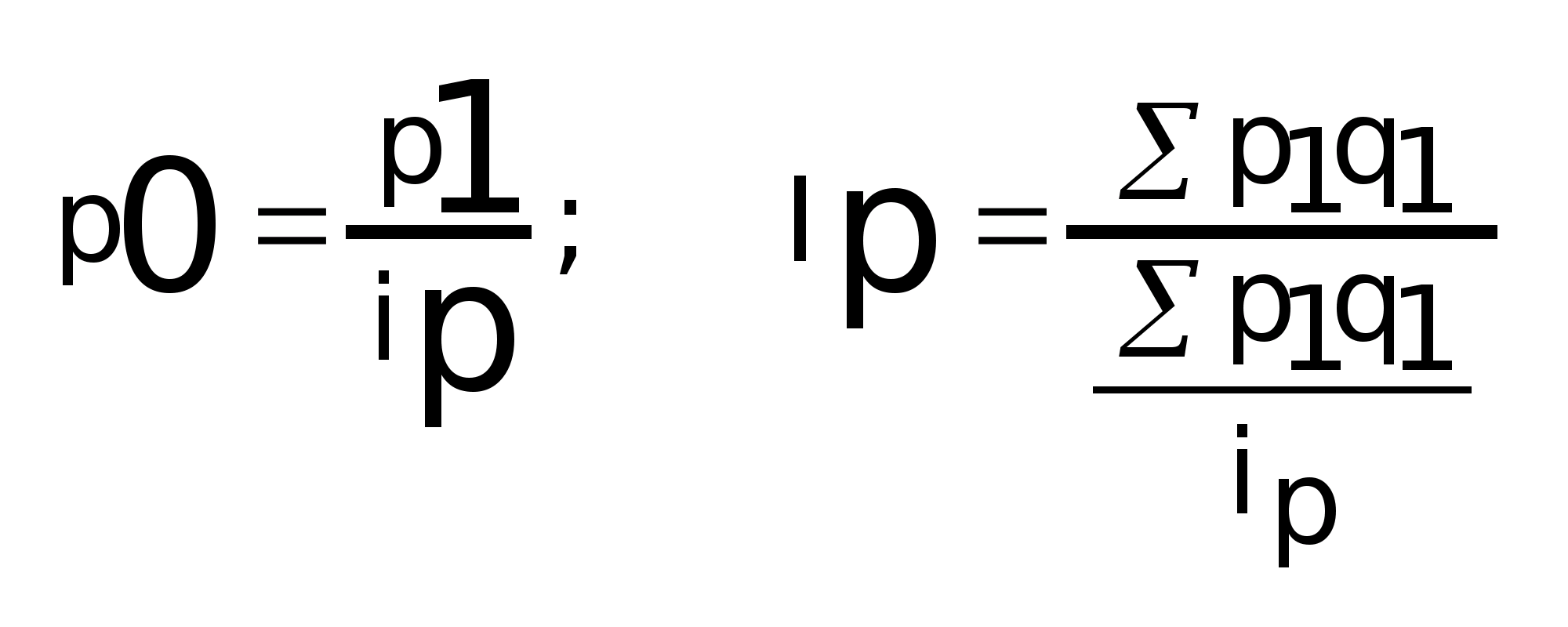 Индекс
цен Ласпейреса:
Индекс
цен Ласпейреса:
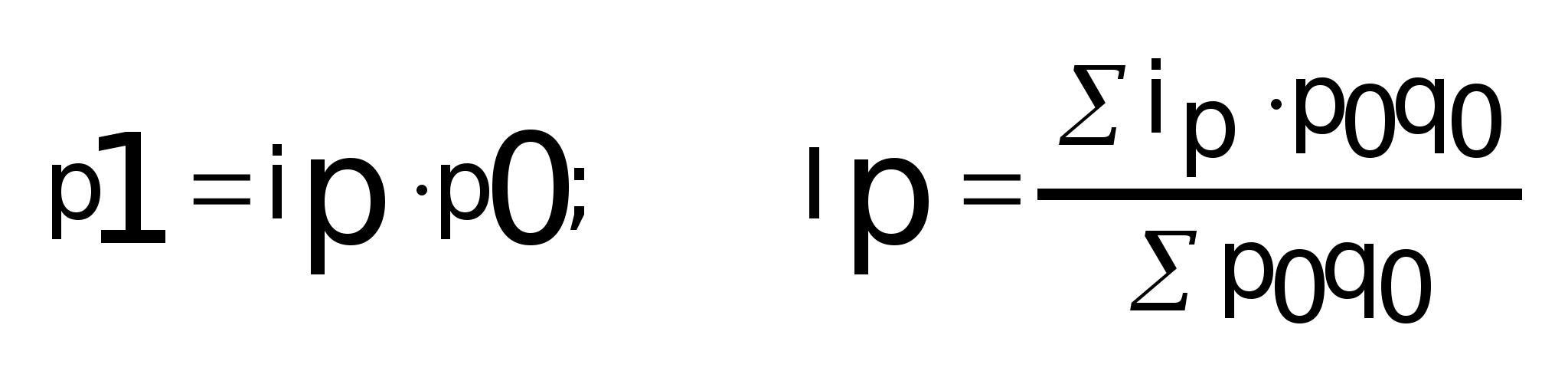
Индекс цен переменного и постоянного состава
3.1.Индекс
переменного состава: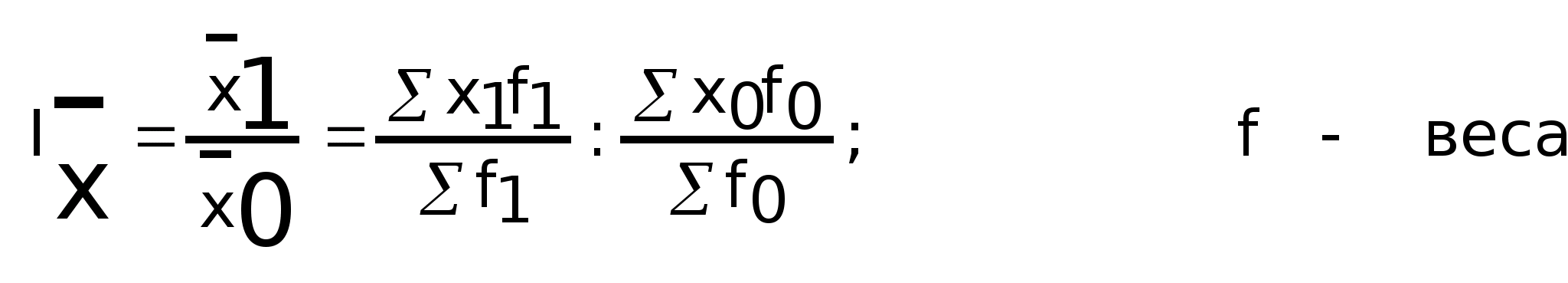 Индекс
постоянного состава:
Индекс
постоянного состава:
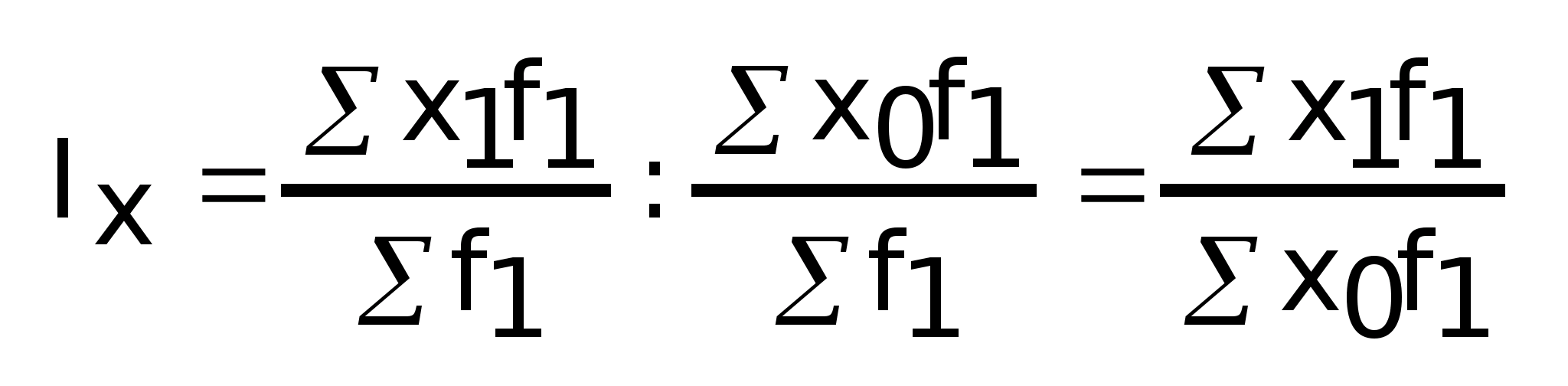 Индекс
структурных сдвигов
Индекс
структурных сдвигов
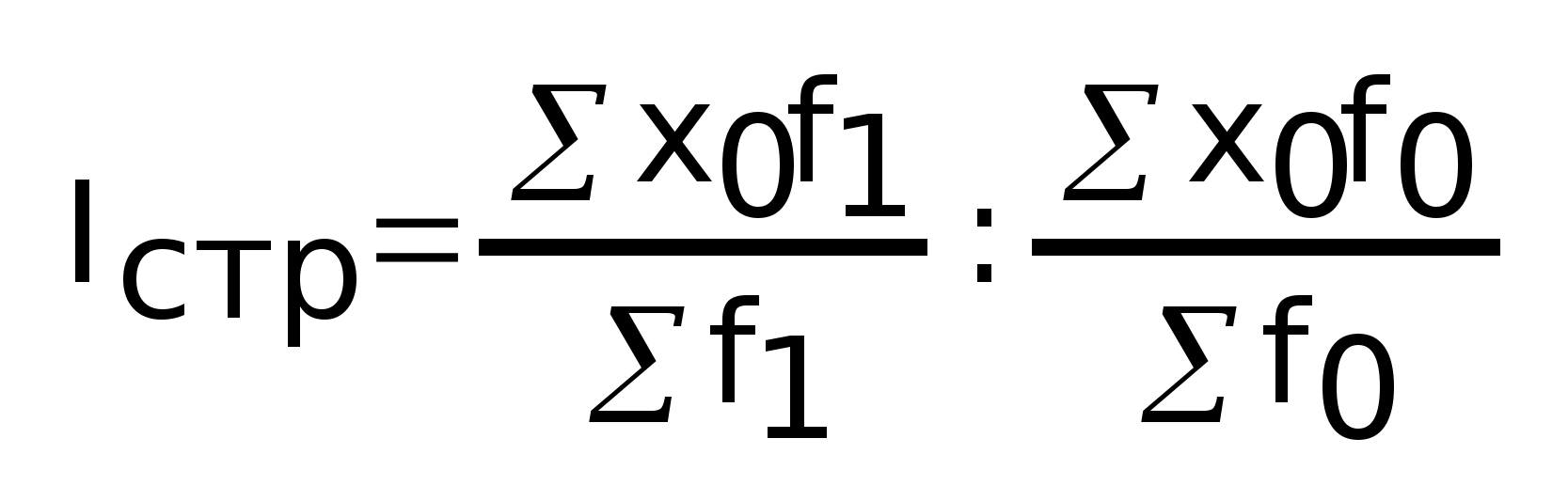
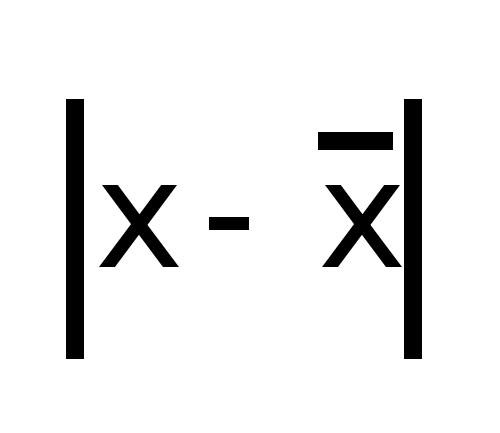 f
f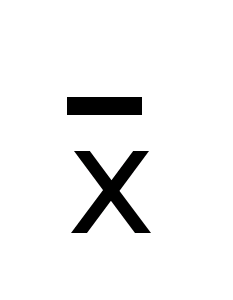 )2
)2 )2
)2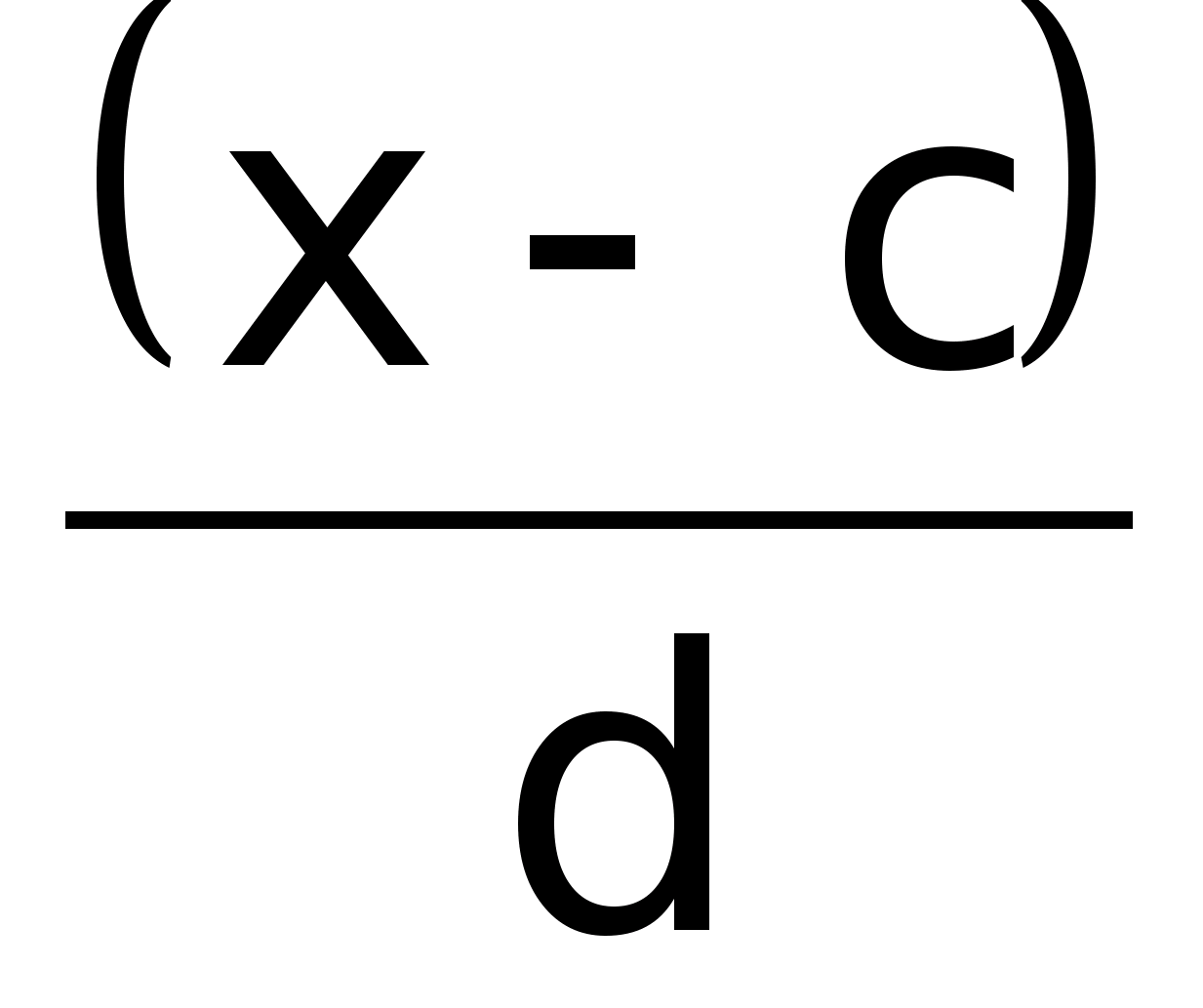
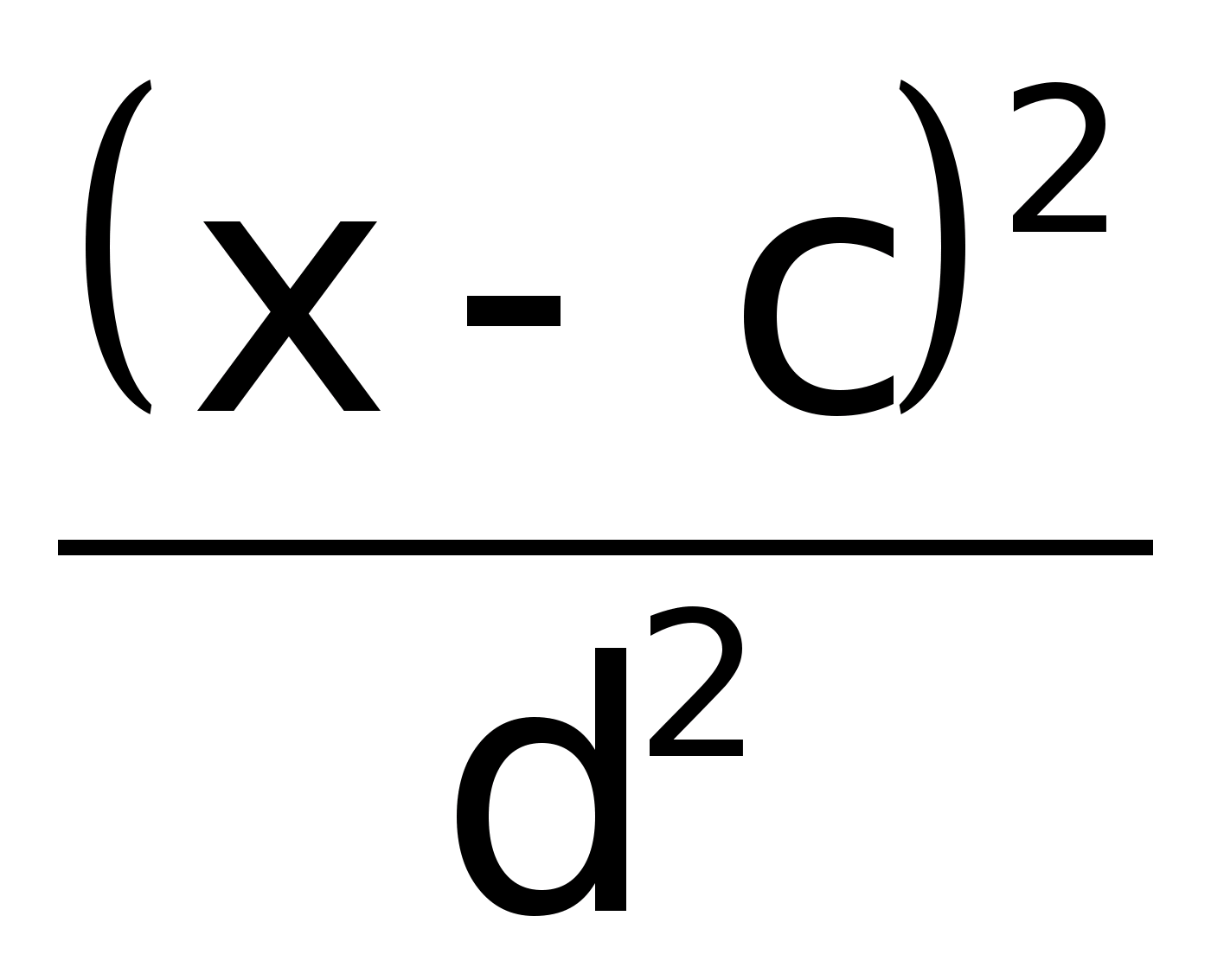
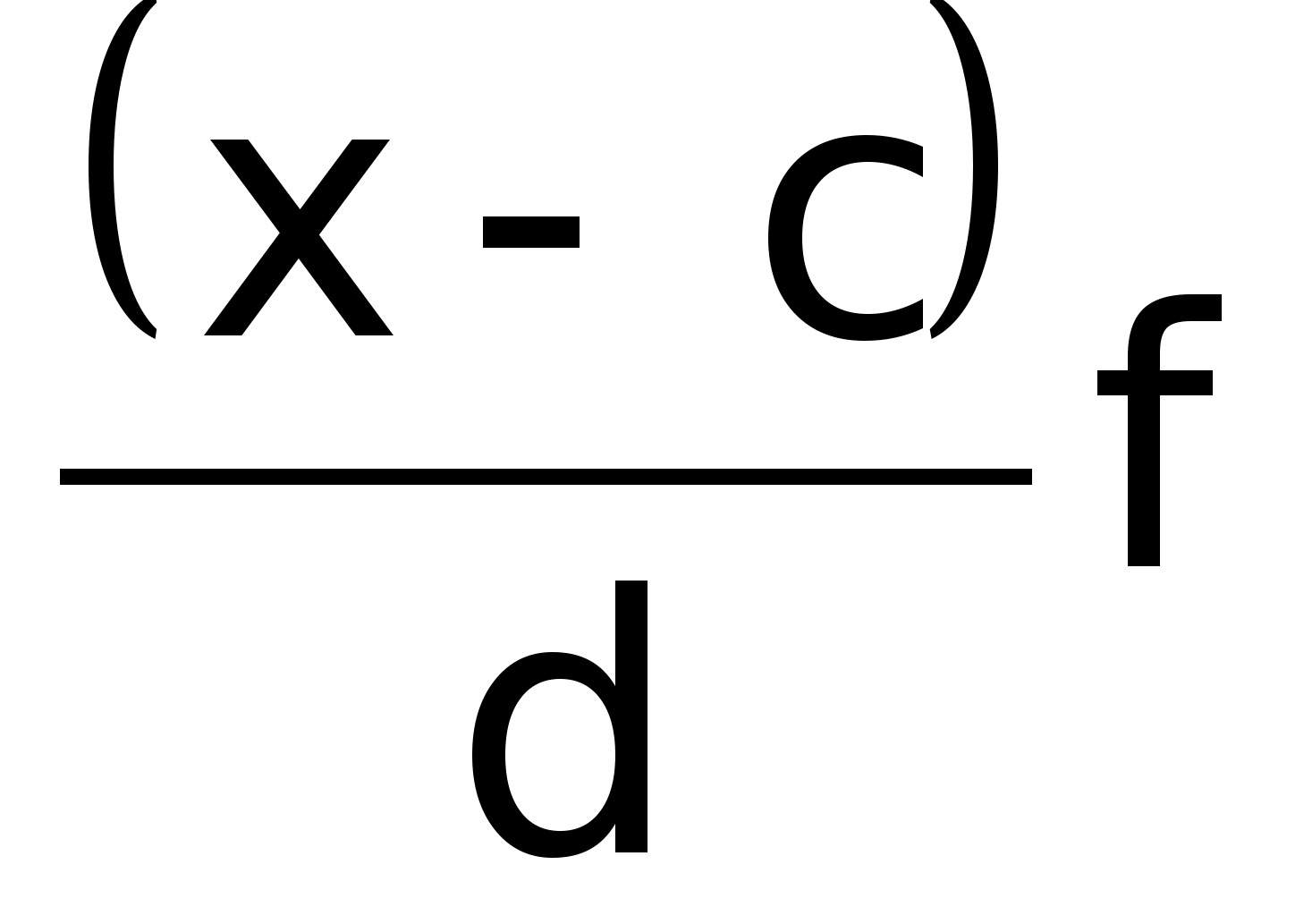
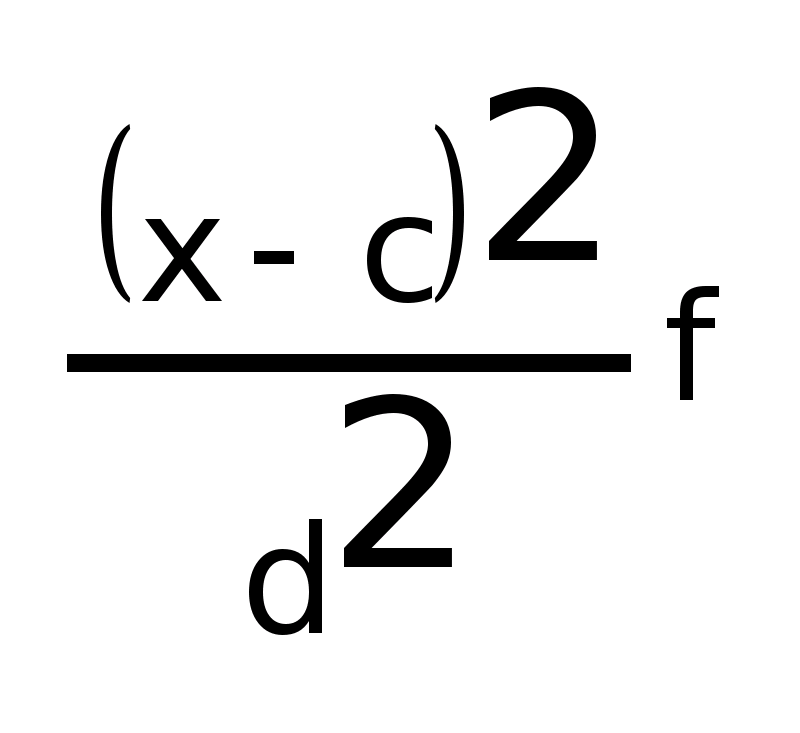
 астота
f
вероятность
астота
f
вероятность