Системы линейных уравнений (работа 1)
Системы линейных уравнений
1. Критерий совместности
Система линейных уравнений имеет вид:
a>11>x>1> + a>12>x>2> + ... + a>1n>x>n> = b>1>
a>21>x>1> + a>22>x>2> + ... + a>2n>x>n> = b>2> (5.1)
... ... ... ... ... ... ... ... ... ... ...
a>m1>x>2> + a>m2>x>2> +... + a>mn>x>n> = b>m>
Здесь а>ij> и b>i> (i =
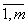 ;
j =
;
j =
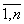 )
- заданные, а x>j> - неизвестные
действительные числа. Используя понятие
произведения матриц, можно переписать
систему (5.1) в виде:
)
- заданные, а x>j> - неизвестные
действительные числа. Используя понятие
произведения матриц, можно переписать
систему (5.1) в виде:
AX = B, (5.2)
где A = (а>ij>) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы, X = (x>1>, x>2>,..., x>n>)T,
B = (b>1>, b>2>,..., b>m>)T - векторы-столбцы, составленные соответственно из неизвестных x>j> и из свободных членов b>i>.
Упорядоченная совокупность n вещественных чисел (c>1>, c>2>,..., c>n>) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x>1>, x>2>,..., x>n> каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c>1>, c>2>,..., c>n>)T такой, что AC ≡ B.
Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Матрица
à =
 ,
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.
Вопрос о совместности системы (5.1) решается следующей теоремой.
Теорема Кронекера- Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и Ã совпадают, т.е.
r(A) = r(Ã) = r.
Для множества М решений системы (5.1) имеются три возможности:
1) M = Ø (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда
r(A) = n. При этом число уравнений - не меньше числа неизвестных (m ≥ n); если m > n, то m-n уравнений являются следствиями остальных. Если 0 < r < n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a>11>x>1> + a>12>x>2> + ... + a>1n>x>n> = b>1>
a>21>x>1> + a>22>x>2> + ... + a>2n>x>n> = b>2> (5.3)
... ... ... ... ... ... ... ... ... ...
a>n1>x>2> + a>n2>x>2> + ... + a>nn>x>n> = b>n>
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера;3) матричным методом.
2. Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
3. Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
Δ = det (a>ij>)
и n вспомогательных определителей Δ>i>
(i =
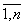 ),
которые получаются из определителя Δ
заменой i-го столбца столбцом свободных
членов.
),
которые получаются из определителя Δ
заменой i-го столбца столбцом свободных
членов.
Формулы Крамера имеют вид:
Δ · x>i> = Δ>i> (i =
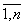 ).
(5.4)
).
(5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x>i> = Δ>i> / Δ.
Если главный определитель системы Δ и
все вспомогательные определители Δ>i>
= 0 (i =
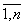 ),
то система имеет бесчисленное множество
решений. Если главный определитель
системы Δ = 0, а хотя бы один вспомогательный
определитель отличен от нуля, то система
несовместна.
),
то система имеет бесчисленное множество
решений. Если главный определитель
системы Δ = 0, а хотя бы один вспомогательный
определитель отличен от нуля, то система
несовместна.
4. Матричный метод
Если матрица А системы линейных уравнений невырожденная, т.е.
det A ≠ 0, то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа