Преобразование случайных сигналов в безынерционных нелинейных и инерционных линейных цепях

КАЗАНСКИЙ ГОСУДАРСТВЕНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А. Н. ТУПОЛЕВА

Институт радиоэлектроники и телекоммуникаций

Кафедра РИИТ

КУРСОВАЯ РАБОТА

по курсу: «Радиотехнические цепи и сигналы»

на тему: «Преобразование случайных сигналов в безинерционных нелинейных и инерционных линейных цепях»

Выполнил: Мулюков Р. Р.

Группа: 5201

Проверил: Козлов В.А.

Казань 2010

Задание

    Произвести генерацию случайного сигнала X(n) с равномерным законом распределения, заданным математическим ожиданием m>X>>0> и среднеквадратическим отклонением >X>>0>.

    Изменяя длину участка реализации N (1 N 1024) определить с помощью критерия 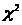такую длину участка реализации N>0>, для которой вероятность Р, с которой статическое распределение выборки из N значений может считаться соответствующий теоретическому распределению, будет достаточно близка к единице, а величины m>XN>>0> и >XN>>0> достаточно близки к заданным m>X>>0> и >X>>0>. В дальнейшей работе использовать этот объем выработки.

    Определить корреляционную функцию R>x>() и энергетический спектр W>x>() исходного сигнала X(n), построить их графики указав масштаб по осям времени и частот соответственно. Определить тип случайного процесса X(n) – широкополосный или узкополосный.

    Аппроксимировать закон распределения случайного процесса X(n). По найденной функции Р(х) и указанной в задании нелинейной характеристике Y = f(x) определить теоретически функцию P(y) – закон распределения отклика безынерционного нелинейного элемента на воздействие случайного элементы X(n). Построить график функции P(y)

    Провести преобразование случайного процесса X(n) в безынерционной нелинейной цепи с указанной в индивидуальном задании нелинейной характеристикой Y = f(x). Для выборки N>0> значений случайного процесса Y(n) получить m>1>>YN>>0> и >1>>YN>>0>, гистограмму, графики корреляционной функции R>y>() и энергетического спектра случайного сигнала W>y>(). Сопоставить гистограмму с графиком функции P(y). Указать, какие характеристики случайного процесса изменились в результате его передачи через безынерционную нелинейную цепь.

    Провести фильтрацию случайного процесса Y(n) цифровой моделью инерционной линейной цепи в индивидуальном задании характеристиками получили новый сигнал Z(n). Для выборки N>0> значений случайного процесса Z(n) получить m>1>>ZN>>0> и >1>>ZN>>0>, гистограмму, графики корреляционной функции R>z>() и энергетического спектра W>z>(). Определить с помощью критерия x2 произошла ли нормализация случайного процесса Y(n) в результате его фильтрации в линейной цепи. Указать, какие характеристики случайного процесса изменились в результате его передачи через линейную цепь.

Параметры исходного сигнала X(n)

Вариант 27

m>XN>>0> = -1,25 >XN>>0> = 0,75 Т = 0.0004 с

Вариант нелинейности 3.4

Нелинейности

Y =

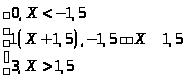
Параметры линейной цепи

Тип ПФ f0 = 500 Гц Q = 3

    Случайными называются сигналы (процессы), значение которых не могут быть предсказаны с полной достоверностью. Наибольшее распространение при описании случайных сигналов имеют математическое ожидание m>1>>X>>0> = -1,25 (начальный момент 1-го порядка) и среднеквадратичное отклонение >X>>0> = 0,75 (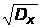, где D>x> – дисперсия [центральный момент 2-го порядка]). 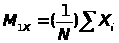Если реализация случайного процесса X(t) задана в виде выборочной последовательности значений X>i>>,> где i = 1,2,3, … N, то 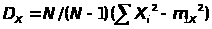математическое ожидание рассматривать как постоянную составляющую в спектре случайного сигнала, а дисперсию как среднюю мощность флуктуационной (переменной) составляющей.

    Одной из важнейших характеристик случайного процесса является плотность вероятности P(х) – функция, которая показывает, насколько часто повторяется (по времени) то или иное значение Х.

Для равномерного закона распределения

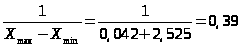
P



X>min> = -2,525 0 X>max> = 0,042 X> >

Все значения в Х интервале от X>min> до X>max> встречаются одинаково часто.

Для точного определения одномерной плотности случайного процесса необходимо исследовать реализацию бесконечной длительности, что на практике нереально. Поэтому реально берут реализацию конечной длительности Т>с> и при ее изучении берут выборки с конечным шагом Т (в данной работе Т = 0.0004 с), число отсчетов случайного сигнала 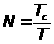, подвергаемых обработке, всегда конечно, следовательно, вместо P(х) получают ее оценку в виде ее гистограммы.

Изменяя длину участка реализации N (1 N 1024) определим с помощью критерия 2 такую длину участка реализации N>0>, для которой вероятность Р, с которой статистическое распределение выборки из N значений может считаться соответствующим теоретическому распределению, будет достаточно близка к единице, а величины m>XN>>0> и >XN>>0> достаточно близки к заданным m>X>>0> и >X>>0>.

Если реализация случайного процесса X(t) задана в виде выборочной последовательности значений X>i>>,> где i = 1,2,3, … N, то для построения гистограммы находят X>min> и X>max>. Затем диапазон изменений X(X>min>  X>max>) разбивают на отдельные интервалы ширины X. Число интервалов N>i> берут,

10  20.

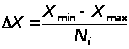
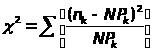
где n>k> – число отсчетов сигнала, попавший в k – интервал, 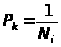- теоре-тическая вероятность пребывания случайного сигнала в пределах каждого из интервалов X (в работе N>i> = 10), N – общее число исследуемых отсчетов сигнала.

Пусть N = 100 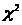= 3,6 m>XN>>0> = -1,1635 >XN>>0> = 0,7464

Пусть N = 200 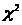= 9,8 m>XN>>0> = -1,1533 >XN>>0> = 0,7572

Пусть N = 300 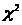= 10,6 m>XN>>0> = -1,1803 >XN>>0> = 0,7569

Пусть N = 400 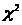= 8,8 m>XN>>0> = -1,2014 >XN>>0> = 0,7597

Пусть N = 500 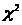= 6,68 m>XN>>0> = -1,2082 >XN>>0> = 0,7452

Пусть N = 600 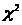= 8,07 m>XN>>0> = -1,2143 >XN>>0> = 0,7416

Пусть N = 700 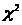= 6,4 m>XN>>0> = -1,2196 >XN>>0> = 0,7471

Пусть N = 800 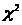= 5,77 m>XN>>0> = -1,2368 >XN>>0> = 0,7443

Пусть N = 900 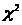= 7,51 m>XN>>0> = -1,2265 >XN>>0> = 0,7480

Пусть N = 1000 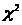= 7,48 m>XN>>0> = -1,2119 >XN>>0> = 0,7473

В дальнейшей работе будем использовать объем выработки N = 100, т. к. критерий Пирсона имеет наименьшее значение.

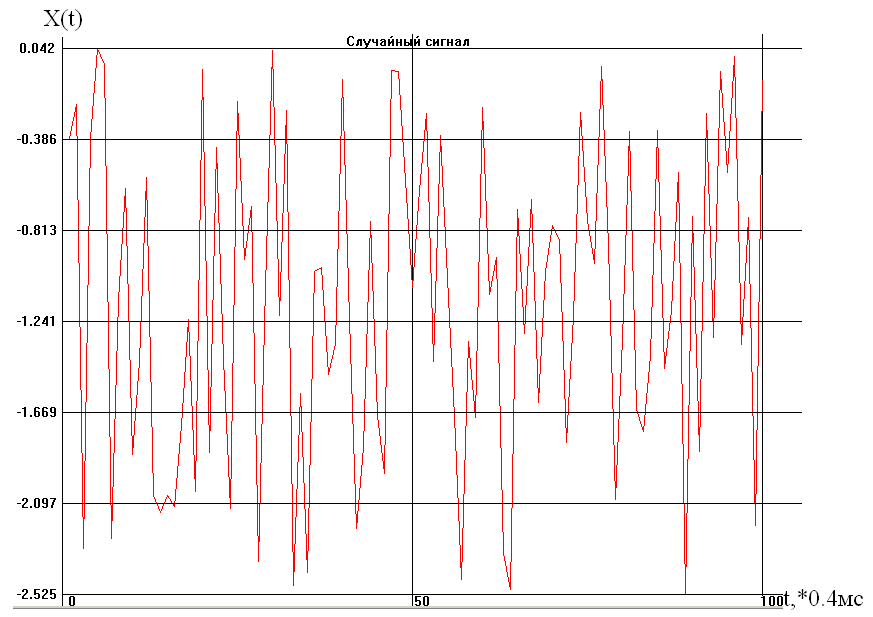
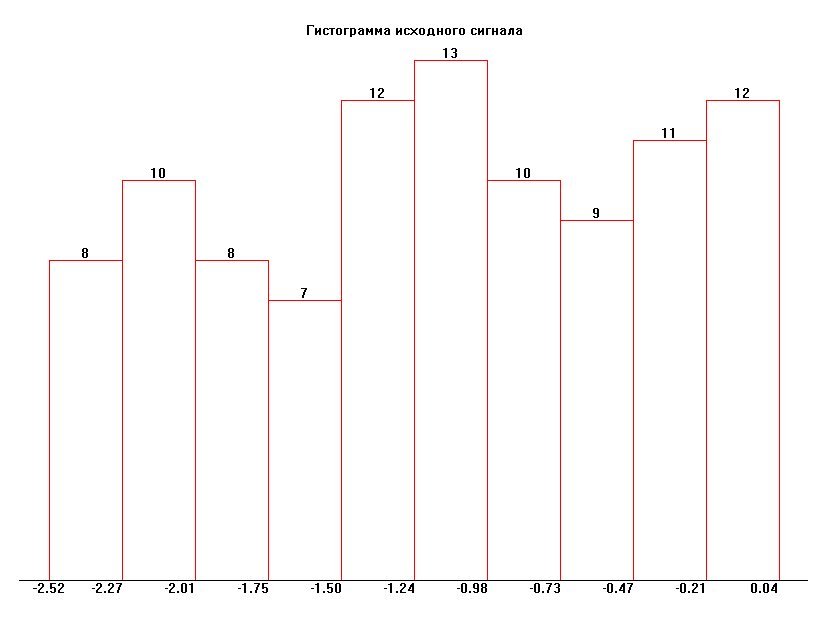
    Энергетический спектр случайного сигнала W>x>() показывает, как средняя мощность сигнала распределена по диапазону частот. Для большинства случайных сигналов ширина спектра теоретически бесконечно велика. Для оценки реальной ширины спектра вводят понятие эффективной ширины спектр >э>, которую можно определить как полосу частот, в пределах которой спектральная плотность средней мощности падает не более чем в 2 раза по сравнению с максимумом.

Корреляционная функция случайного процесса R>х>() является внутренней мерой связанности процесса в различные моменты времени, отстоящие на , его свойства (помнить) предшествующие состояния следует интервал корреляции – это величина временного сдвига , начиная с которого значения сигнала X(t) и X(t+) могут считаться несвязанными.

Оценку величин интервала корреляции процесса >к> при известной корреляционной функции R>х>() можно следующим образом: если процесс широкополосный, то >к> равен координате первого нуля функции R>х>(); если процесс узкополосный, то >к> определяют по координате первого нуля огибающей функции R>х>(). Корреляционная функция R>х>() и энергетический спектр случайного сигнала W>x>() связана между собой преобразованиями Фурье. Если реализация случайного процесса X(t) задана в виде выборочной последовательности значений X>i>>, >где i = 1,2,3, … N, то

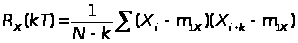, 0 k N>1>

где N>1> – число отсчетов корреляционной функции и энергетического спектра (на 1  2 порядка меньше числа отсчетов сигнала N);

Т – интервал дискретизации сигнала.

 = 2Пf = 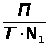- шаг отсчета по частоте.

Корреляционная функция R>х>(t) и энергетический спектр W>x>(f) исходного сигнала изображены на рисунках (см. ниже). Это широкополосный сигнал. Т = 0.0004с; N>1> = 10;

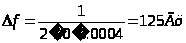
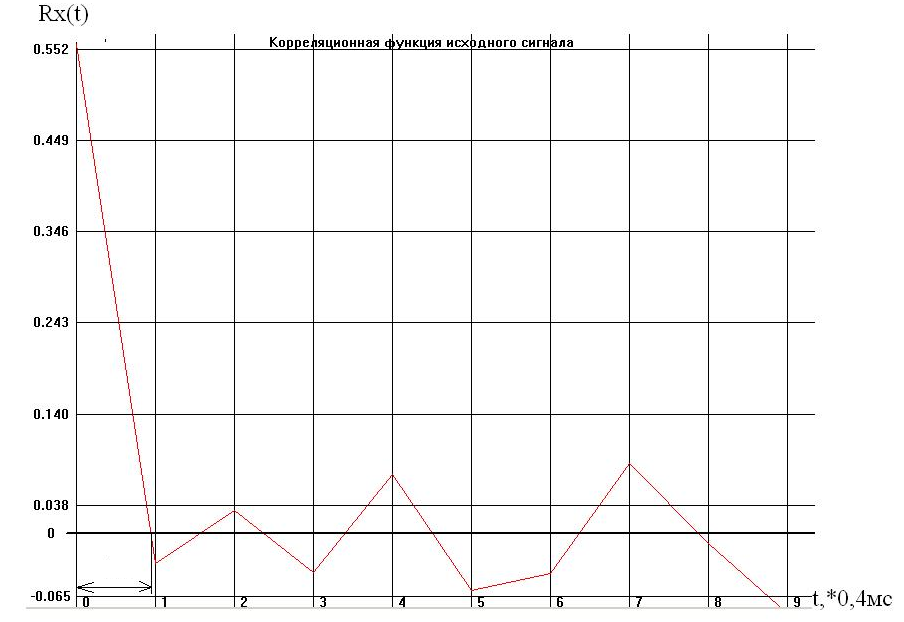
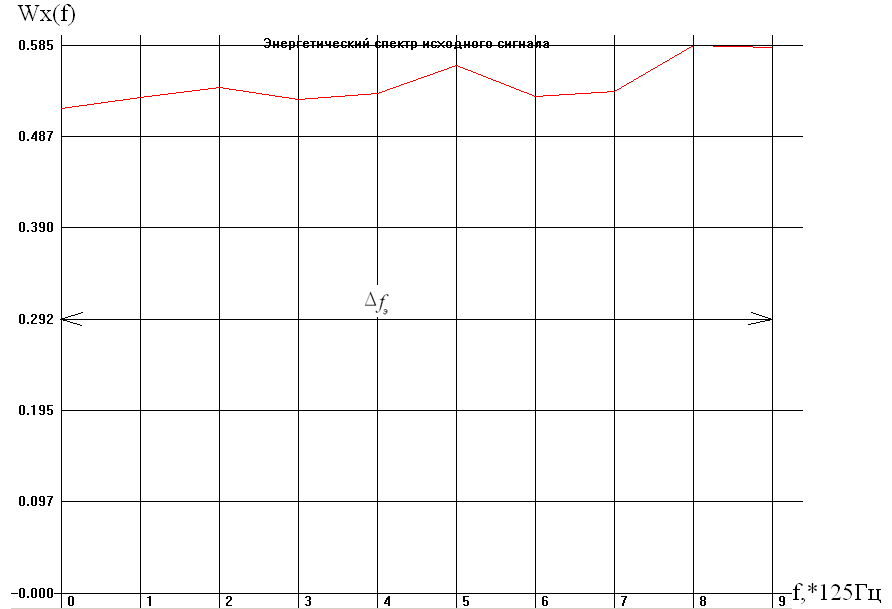
По графику корреляции видно что исследуется широкополосный сигнал, его интервал корреляции:

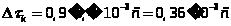
Энергетическая ширина спектра

4. Найдем P(x) для равномерного закона распределения

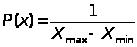
X>min> = -2,525 X>max> = 0,042

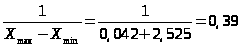
Если во всей области изменения переменной Х связь отклика Y с воздействием Х, обусловленная видом характеристики y = f(x) нелинейного элемента, однозначна, то плотность вероятности распределения мгновенных значений P(y) по известной P(x) можно найти

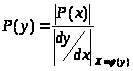
где 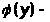преобразованная зависимость y = f(x).

Если нелинейность такова, что какому-то значению y = y>1> отвечает конечное множество значений

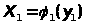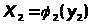, , … , то

++ …

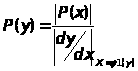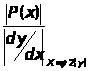Если линейность такова, что есть значения Y, которым в силу характеристики y = f(x) отвечает бесконечное число значений Х, то применяют следующее правило

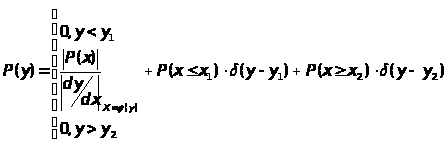
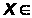[-2,525; 0,042] 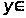[0, 3] P(x) = 0,39

У нас нелинейность вида

Y =

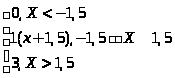
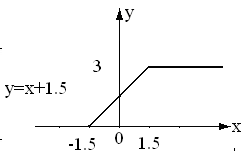
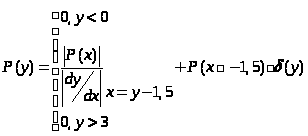
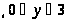
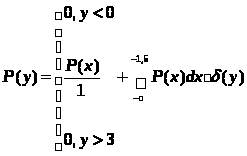
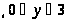
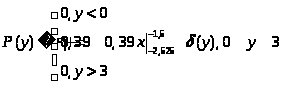
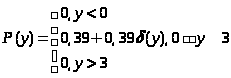
В результате преобразования случайного процесса X(n) в безынерционной нелинейной цепи мы получили новый сигнал Y(n).

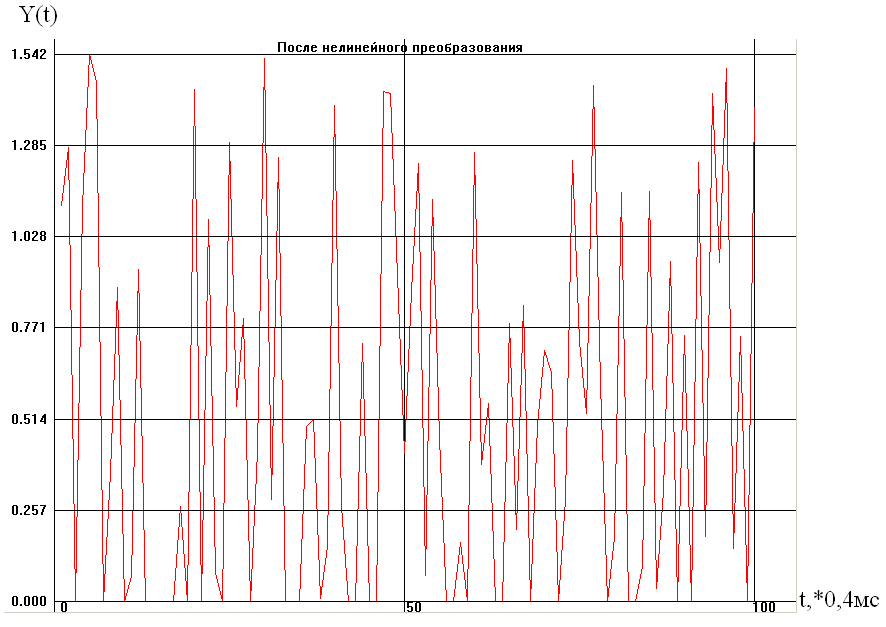
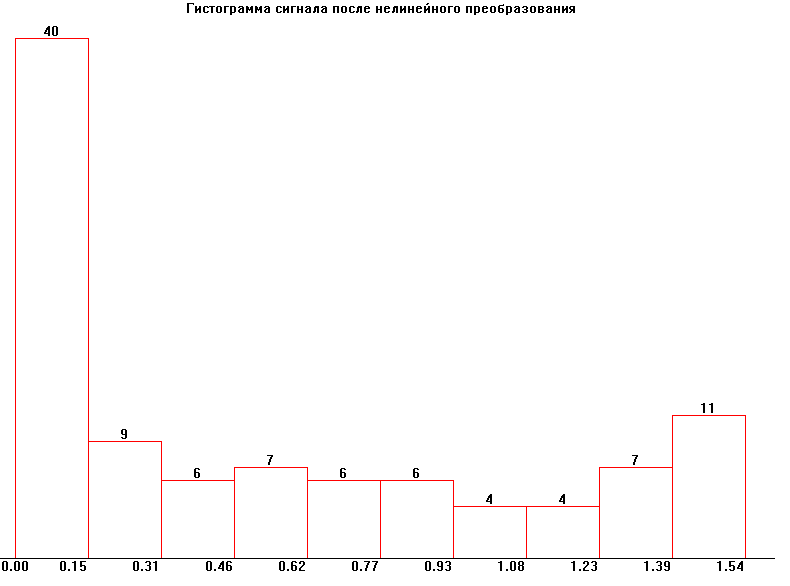
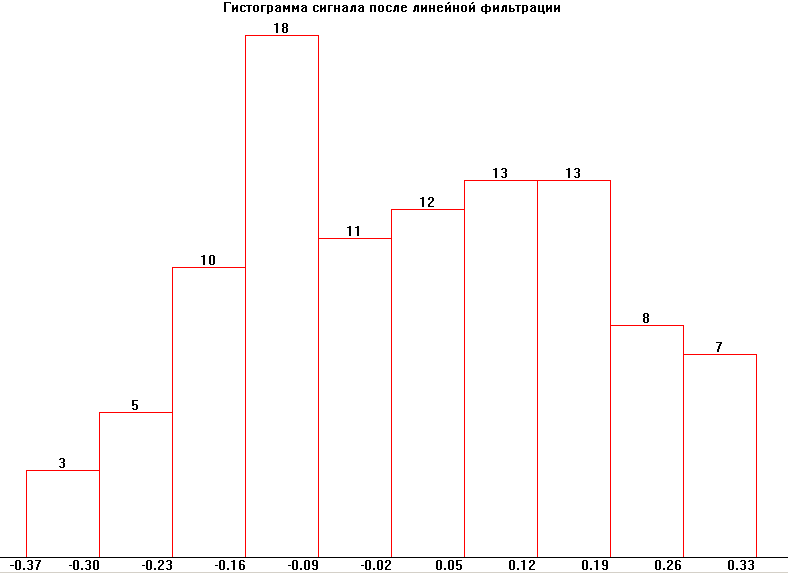
Для него m>1>>YN>>0> = 0,5132 >1>>YN>>0> = 0,5323 Гистограмма изображена на рисунке, ее огибающая схожа с графиком теоретически построенной функции P(y) следовательно, теоретические расчеты совпадают с практическим преобразованием.

Корреляционная функция R>y>(t) и энергетический спектр случайного сигнала W>y>(f) представлены на рисунках, приведенных ниже:

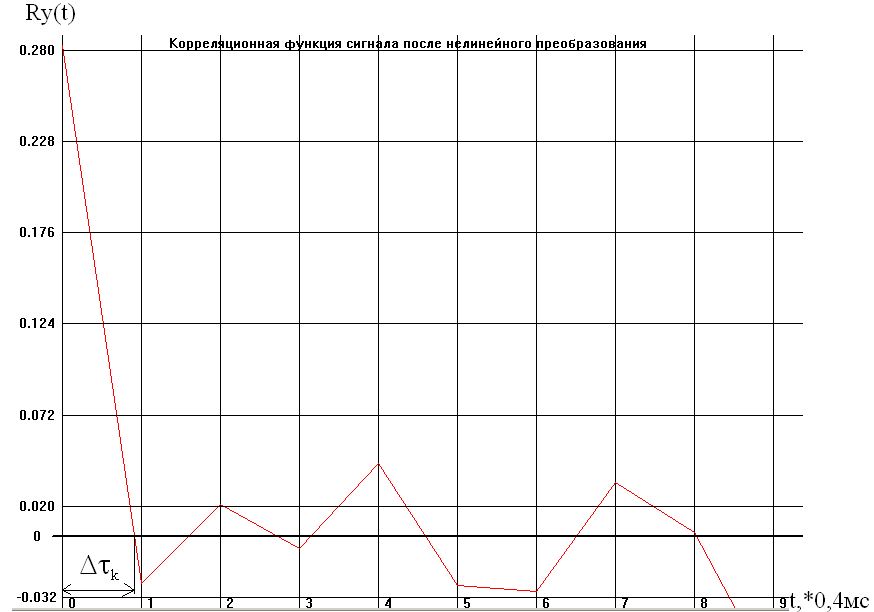
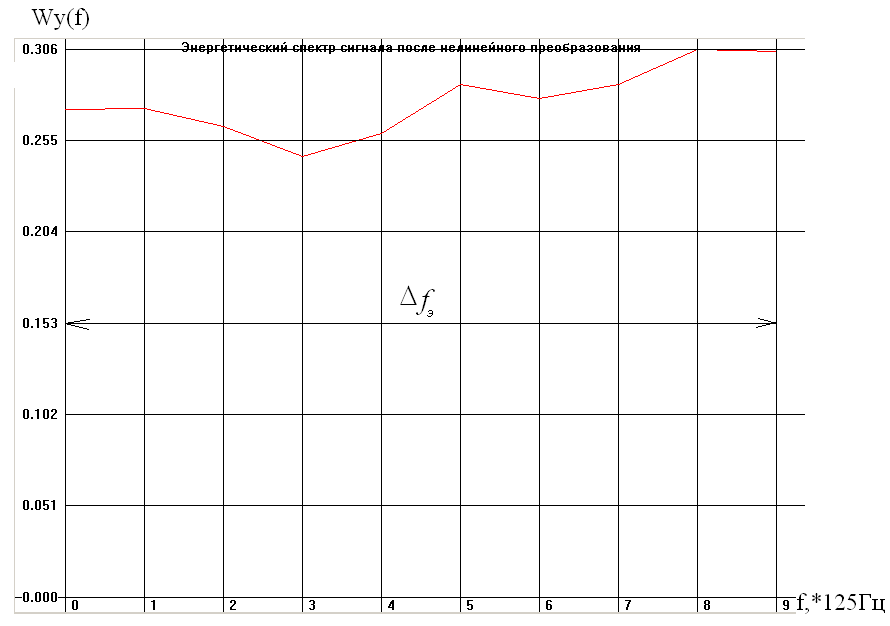
Интервал корреляции:

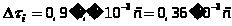
Энергетическая ширина спектра:

В результате преобразования случайного процесса X(n) в безынерционной нелинейной цепи случайный сигнал перестал быть равномерным. Математическое ожидание увеличилось и стало больше нуля. Среднеквадратичное отклонение уменьшилось примерно в 1,5 раза. Сигнал остался широкополосным.

6. В общем случае точно установить взаимосвязь закона распределения воздействия с законом распределения отклика линейной цепи и ее частотной характеристикой очень сложно. Но если протяженность во времени импульсной характеристики цепи такова, что хотя бы в несколько раз превышает >к> входного случайного процесса, или полоса пропускания цепи в частотной области хотя бы в несколько раз меньше ширины энергетического спектра входного процесса, то при любом законе распределения P(х) входного процесса, случайный процесс на выходе линейной цепи будет иметь распределение, близкое к нормальному.

В результате фильтрации случайного процесса Y(n) в инерционной цепи (ПФ, f0 = 500 Гц, Q = 3) мы получили новый сигнал Z(n).

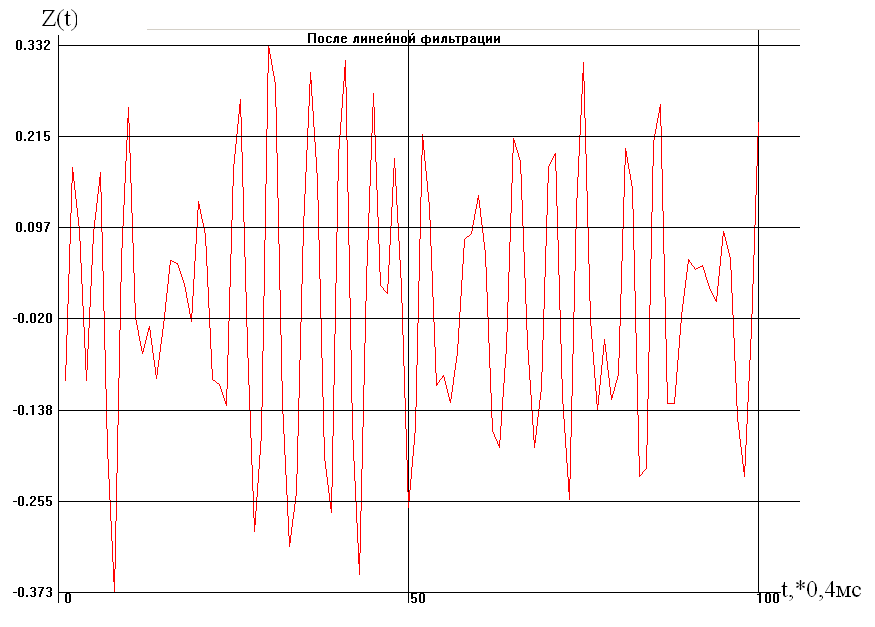
Для него m>1>>ZN>>0> = 0,0018 >1>>ZN>>0> = 0,1679

Определим по гистограмме с помощью критерия 2 произошла ли нормализация случайного процесса Y(n) в результате его фильтрации в линейной цепи

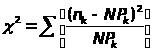
где n>k> – число отсчетов сигнала, попавший в k – интервал.

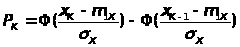
- теоретическая вероятность пребывания случайного сигнала в пределах каждого из интервалов X, N - общее число исследуемых отсчетов сигнала N>i> = 10

P=Ф(-1,8)-Ф(-2,21)= - 0,92814+0,97289=0,045

Р=Ф(-1,38)+Ф(1,8)=-0,83241+0,92814=0,096

Р=-Ф(0,96)+Ф(1,38)= -0,66294+0,83241=0,1694

Р=-Ф(0,55)+Ф(0,96)= -0,41768+0,66294=0,24526

Р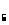=-Ф(0,13)+Ф(0,55)=-0,10348+0,41768=0,3142

Р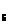=Ф(0,29)+Ф(0,13)=0,22818+0,10348=0,33166

Р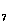=Ф(0,7)-Ф(0,29)=0,51608-0,22818=0,28789

Р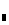=Ф(1,12)-Ф(0,7)=0,73729-0,51607=0,22122

Р9=Ф(1,54)-Ф(1,12)=0,87644-0,73729=0,13915

Р10=Ф(1,95)-Ф(1,54)=0,94882-0,87644=0,07

K

P>k>

n>k>

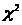
1

0,045

3

4,9

2

0,0096

5

2,5

3

0,1694

10

0

4

0,24526

18

6,4

5

0,3142

11

0,1

6

0,33166

12

0,4

7

0,28789

13

0,9

8

0,22122

13

0,9

9

0,13915

8

0,4

10

0,07

7

0,9

2 =17,4 Нормализация Р случайного процесса Y(n) в результате его фильтрации в линейной цепи не происходит.

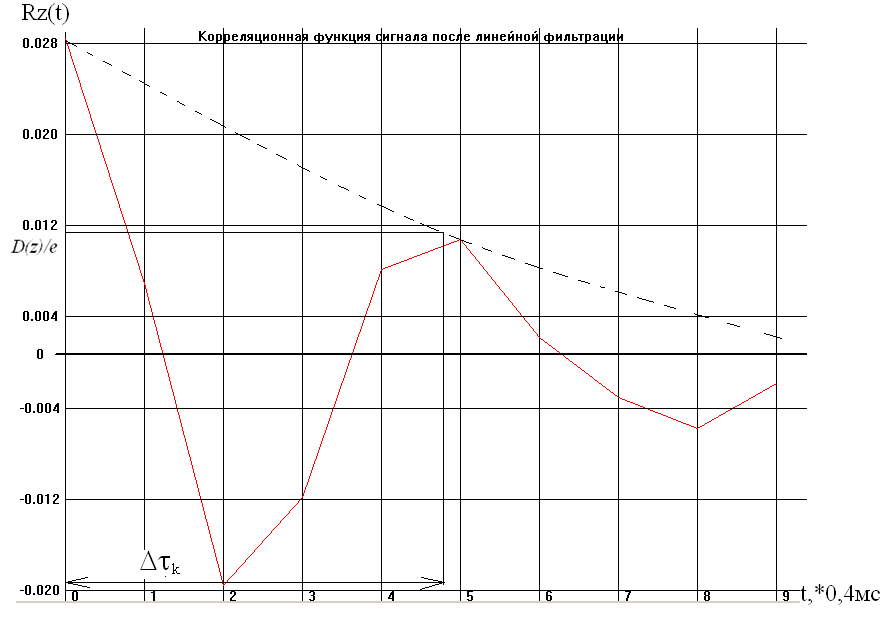
Графики корреляционной функции и энергетического спектра представлены ниже:

Интервал корреляции:

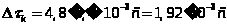
Энергетическая ширина спектра:

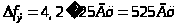
В результате фильтрации случайного процесса Y(n) в инерционной линейной цепи случайный сигнал становится близким к нормальному. К этому заключению приходим из того, что полоса пропускания цепи в частотной области почти в 2 раза меньше ширины энергетического спектра входного процесса. Математическое ожидание стало равно 0, 0018, а среднеквадратическое отклонение уменьшилось до 0,1679. Сигнал стал узкополосным – это произошло из-за частотной характеристики К() линейной цепи – ПФ.

Выводы

    При взятой длине реализации N = 100, 2 является наименьшим из всех рассмотренных N>.> Математическое ожидание отличается на 9% от заданного, а среднеквадратическое отклонение на 1%

    По виду корреляционной функции и энергетическому спектру заключаем, что сигнал широкополосный.

    В результате преобразования случайного процесса X(n) в безинерционной нелинейной цепи, случайный сигнал перестал быть равномерным. Математическое ожидание увеличилось и стало больше 0, среднеквадратичное отклонение уменьшилось примерно в 1,5 раза. Сигнал остался широкополосным, >к> и f>э> остались прежними.

    В результате фильтрации случайного процесса Y(n) в инерционной цепи нормализация не произошла. Математическое ожидание стало равным 0,0018, а среднеквадратическое отклонение 0,1679. Сигнал стал узкополосным, энергетическая ширина спектра составил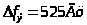а

, а

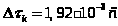
Литература

1) Козлов В.А. Преобразование случайных сигналов в безынерционных нелинейных и инерционных линейных цепях. Казань, КГТУ им. А.Н. Туполева, 2001 г.

2) Гоноровский И.С. Радиотехнические цепи и сигналы. М, Советское радио. 1977 г.